ABSTRACT

In this paper, we are concerned with the solvability for a class of nonlinear sequential fractional dynamical systems with damping infinite dimensional spaces, which involves fractional Riemann-Liouville derivatives. The solutions of the dynamical systems are obtained by utilizing the method of Laplace transform technique and are based on the formula of the Laplace transform of the Mittag-Leffler function in two parameters. Next, we present the existence and uniqueness of solutions for nonlinear sequential fractional dynamical systems with damping by using fixed point theorems under some appropriate conditions.

Keywords:

Solvability, Sequential Fractional Equations, Mittag-Leffler Function, Gramian matrix, Fixed Point Theorems

1. Introduction

The purpose of this paper is to study the solvability of the following nonlinear sequential fractional dynamical systems which involve fractional Riemann- Liouville derivatives with damping:

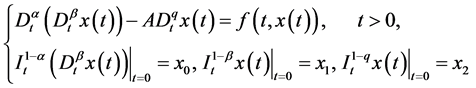(1.1)

In 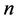dimensional Euclidean space, where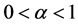, , 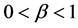, , 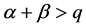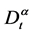is the standard Riemann-Liouville fractional derivative with the lower limit zero, and denotes the sequential Riemann-Liouville fractional derivative presented by Miller and Ross in [1]. is a vector, a sufficiently order differentiable function; 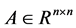is an any matrix and 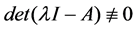; 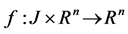is a continuous function.

The theory of the fractional derivatives and integrals becomes increasingly more important for applications. Both the ordinary and the partial differential equations of fractional order have been used within the last few decades for modeling of many physical and chemical processes and in engineering (see [1] [2] [3] [4] [5] [6]) and references therein). As stated in [6] [7], partial fractional differential equations became especially important for the modeling of the so called anomalous phenomena in nature and in the theory of the complex systems. Moreover, fractional differential equations allow for the representation of the long-memory and non-local dependence of many processes.

In this connection, the so-called time-fractional diffusion equation that is obtained from the classical diffusion equation by replacing the first-order time derivative by a fractional derivative of order 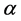with 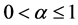has to be especially mentioned. As a consequence, the time-fractional diffusion equation appeared to be a suitable mathematical model for the so-called sub-diffusion processes and thus became important and useful for different applications. For more details on this topics one can see for instance (see [8] [9] [10]) and the reference therein.

Fractional derivatives have been recognized as one of the best tools to describe long-memory processes. The corresponding mathematical models of these processes are fractional differential equations, which have been considered as an alternative model to integer differential equations. Recently, the subject of fractional differential equations is gaining much importance and attention. For more history and basic results on fractional calculus theory, one can see monograph ([4] [11]-[21]) and the references therein. In the past decades, various results for Cauchy problem, boundary value problem, nonlocal problem, impulsive problem and control problem of Riemann-Liouville type, Caputo type, Hadamard type fractional differential equations or inclusions have been paid more and more attention on finite or infinite dimensional spaces in recent years. In [22], Carrasco and Leiva developed a semi group approach for a class of semilinear parabolic differential equations with delay and then derived the solvability of the delay systems by using the well known fixed point theorem. Leiva, Merentes and Sanchez in [23] showed the solvability of a broad class of semilinear reaction diffusion equations in a Hilbert space. In [24], Li and Zhou considered the solvability for a class of control systems governed by semilinear parabolic equations with a boundary control by using the theorem of operators semi group. Wang and Du in [25] [26] recently proved the solvability of a class of semilinear parabolic system by using the Kakutani fixed point theorem.

Significant progresses have been made for the integer and fractional order differential equations (see [27] [28] [29]). However, to the best of our knowledge, there is still little information known for the solvability of the nonlinear sequential fractional dynamical systems with damping and this fact is the motivation of the present work. Our aim in this paper is to provide some suitable sufficient conditions for the existence and uniqueness of solutions of the nonlinear sequential fractional dynamical systems which involve fractional Riemann- Liouville derivatives with damping.

The rest of this paper is organized as follows: In Section 2, we will present some basic definitions and preliminary facts which will be used throughout the following sections. In Section 3, we establish a suitable concept of solutions for problem (1.1) and present the existence and uniqueness of solutions under some appropriate conditions.

2. Preliminaries

In this section, we introduce some basic definitions and preliminaries which are used throughout this paper. For the 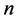-dimensional Euclidean space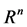, let denote the Banach space of all continuous functions from 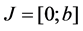into equipped with the norm for and we also introduce the space with the norm. Obviously, the space is a Banach space.

Next, for the convenience of the readers, we first present some useful definitions and fundamental facts of fractional calculus theory, which can be found in [7] [30].

Definition 2.1. The integral

is called Riemann-Liouville fractional integral of order, where is the gamma function.

Definition 2.2. For a function given in the interval the expression

is called the Riemann-Liouville fractional derivative of order q, where, denotes the integer part of number q.

Definition 2.3. 1) The Mittag-Leffler function in two parameters is defined as

where and denotes the complex plane.

In particularly, for we obtain the Mittag-Leffler function in one parameter as:

In addition, the Laplace transform of the Mittag-Leffler function is

where denotes the real parts of.

2) For an matrix, we define the Mittag-Leffler matrix function as follows:

and the Laplace transform of the Mittag-Leffler matrix function is

where is the identity matrix.

In order to study the solutions of problem (1.1), we need:

Lemma 2.4. ([30]) Let and let be the fractional integral of order If and then we have the following equality

Next, the Laplace transform formula for the Riemann-Liouville fractional integral is defined by

where is the Laplace of defined by

is a constant.

Lemma 2.5 Let and if and is a solution of the problem

(2.1)

then, satisfies the following equation

Proof. Apply Riemann-Liouville fractional integral operator on both sides of the equation (2.1), we get

i.e.,

Then by Lemma 2.4, we obtain

(2.2)

It follows from (2.2) that

(2.3)

Next, let taking the Laplace transformations

and

to the Equation (2.3), one can obtain

(2.4)

Taking inverse Laplace transform to both sides of the expression (2.4), then

Finally substituting Laplace transformation of Mittag-Leffler function and Laplace convolution operator, we get the solution of the given system as

(2.5)

This completes the proof of the lemma.

According to Lemma 2.5, we give the following definition:

Definition 2.6. A function is called a generalized solution of (1.1) if it satisfies the following fractional integral equation

3. Existence of Solutions

In this section, we present the existence and uniqueness of solutions for problem (1.1) under some appropriate conditions by a well known fixed point theorem.

To obtain the global existence of mild solutions of problem (1.1), we suppose:

H(f): The function satisfied is continuous for all and there exists a constant such that

.

Now, we are in the position to present the main result of this section.

Theorem 3.1. Assume that the condition H(f) holds. Then the problem (1.1) has a unique solution on

Proof. Define the operator as

Clearly, the problem of finding solutions for system (1.1) is reduced to find the fixed point of F. Firstly, under the assumption of our theorem, it is easy to check that F maps into itself. So it is only need to show that is a contraction operator on.

Let and then for any and we have

(3.1)

Using (3.1) and induction on, it follows easily that

Therefore, we obtain

Since is the general term of the Mittag-Leffler series and this series is uniformly convergent on real axis, then for large enough, one can obtain

Hence, is a contraction operator for large integer and hence. By applying the well-known Banach’s contraction mapping principle, we know that the operator and also has a unique fixed point on So problem (1.1) has a unique solution on. This completes the proof.

Acknowledgements

The authors would like to thank the anonymous reviewers for their careful reviewing and valuable suggestions. This work is supported by National Science Foundation of China (Grant No. 11371125), is also supported by the Natural Science Foundation of the Department of Education of Hunan Province (Grant No. 13A013). The second author is also supported by open fund of Guangxi Key laboratory of hybrid computation, NNSF of China Grants No. 11661001, the Project of Guangxi Education Department grant No. KY2016YB417.

Cite this paper

Xiao, C.E. and Li, X.W. (2017) Solvability of Nonlinear Sequential Fractional Dynamical Systems with Damping. Journal of Applied Mathematics and Physics, 5, 303-310. https://doi.org/10.4236/jamp.2017.52027

References