ABSTRACT

Cordial Volterra integral equations (CVIEs) from some applications models associated with a noncompact cordial Volterra integral operator are discussed in the recent years. A lot of real problems are effected by a delayed history information. In this paper we investigate some properties of cordial Volterra integral operators influenced by a vanishing delay. It is shown that to replicate all eigenfunctions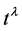, 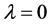or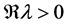, the vanishing delay must be a proportional delay. For such a linear delay, the spectrum, eigenvalues and eigenfunctions of the operators and the existence, uniqueness and solution spaces of solutions are presented. For a nonlinear vanishing delay, we show a necessary and sufficient condition such that the operator is compact, which also yields the existence and uniqueness of solutions to CVIEs with the vanishing delay.

Keywords:

Cordial Volterra Integral Equations, Vanishing Delay, Propositional Delay, Compactness, Existence and Uniqueness

1. Introduction

A kind of Volterra integral equations with weakly singular kernels arisen in 1975 [1] from some heat condition problems with mixed-type boundary conditions is transformed by Watson transforms [2] and the convolution theorem [3]. In [4], the author generalizes such kind of equations into cordial Volterra integral equations (CVIEs) with the form

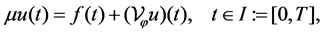(1)

where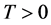, the core 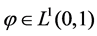and the cordial Volterra integral operator is defined by

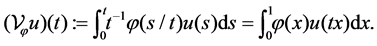
CVIEs appear in a lot of application models, such as Diogo core 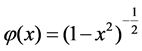, linear Lighthill’s equation (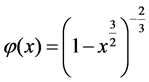), and so on.

It is shown that the cordial Volterra integral operator 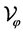in the Banach space 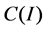is noncompact and its spectrum is a non-countable set, i.e.,

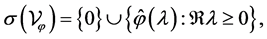
where

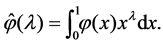
In [5], the author describes the eigenvalues and eigenfucntions of the operator 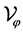on the space 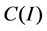when 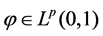with some:

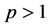1) the point spectrum of 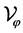is exactly the set;

2) the dimension of the null space is the sum of the multiplicities of the roots of in the complex plane ;

3) the linearly independent eigenfunctions are given by

where is the multiplicity of the root of.

The pure Volterra integral equations with vanishing delay (VIEwND) are initially studied in [6] and a special form of VIEwND, proportional delay differential equations, is widely used in practical applications, for example, electrodynamics [7] [8], nonlinear dynamical systems [9] [10], and also the survey papers [11] [12]. In this paper, we consider the CVIEs with a vanishing delay,

(2)

where is a continuous delay function such that and for all and the operator with delay is similarly defined by

(3)

Besides the existence and uniqueness of solutions to (2), it is more interesting how the eigenvalues and eigenfunctions of the operators are influenced by vanishing delays. In Section 2, we show that the proportional delay, , is the only one that replicates all eigenfunctions, or . For such a delay, we describe the spectrum, eigenvalues and eigenfunctions of the operator. In Section 3, we present a necessary and sufficient condition for the compactness of the operator with a vanishing delay. Based on these discussions, we present the existence, uniqueness and the construction of solutions to (2).

2. Propositional Delays

For a vanishing delay satisfying that

(D1),

(D2) for all,

(D3) is a continuous function in the interval and exists,

the operator (3) is rewritten as the following form

(4)

where the function is a well-defined continuous function in the whole interval. Obviously

and for all.

The cordial Volterra integral operator with a vanishing delay (3) is also written as a cordial Volterra integral operator with a variable kernel, i.e.,

where the discontinuous kernel is defined by

The properties of the operator with continuous kernels are investigated in [13] such as it is compact if and only if. From the above definition, the discontinuous function always satisfies, but the compactness of the operator is influenced not only by the core but also by the value of (see in Corollary 2.3 and Theorem 3.1).

Theorem 2.1. Assume that the function.

1) The operator is a bounded operator from to.

2) If all power-functions or, are eigenfunctions of, then

where for, the integration is defined by

Proof. (i) For, and, there exists a such that

and for all with

,

since is uniformly continuous on the closed interval. The uniform continuity of implies that there exists a such that for all with.

We, without loss of generality, assume that in the following estimation. Then

Hence maps to and its boundedness comes from

2) Without loss of generality, suppose that and for some. Then similarly to the approach in [4], there exists a polynomial such that

Since, is an eigenfunction of,

is also independent of for. Thus

and hence

This contradiction implies the proof is complete.

Remark 2.2. In [4], the author shows that an operator mapping to has the two properties:

1) is a bounded operator;

2) all power-functions, or, are eigenfunctions of;

if and only if is a cordial Volterra integral operator. While including vanishing delays, the two properties only hold for a proportional delay ,.

For a core, we define an integration function of the core by

If for with some (or), then CVIEs naturally reduce to a proportional delay form

(5)

where the corresponding operator has the form with and

Corollary 2.3. Assume that and is a strictly increasing function for. Then a cordial Volterra integral operator with vanishing delays opposites the two properties in Remark 2.2 if and only if the delay is a proportional delay. Of course it is a noncompact operator.

Proof. By Theorem 2.1, one obtains that is a constant. Thus the proof is completed by.

Based on, some more detailed properties on cordial Volterra integral operators with a proportional delay are presented in the following theorem.

Theorem 2.4. Assume that a core with some, , and for. Then

1) The spectrum of is given by

where.

2) The point spectrum of is exactly the set.

3) The dimension of the null space is the sum of the multiplicities of the roots of in the complex plane .

4) The linearly independent eigenfunctions are given by

where is the multiplicity of the root of.

5) The range of the operator is the whole space if and only if.

Both the existence and uniqueness of solutions to (5) are valid when the parameter does not lie in the spectrum of the corresponding operators. On the other hand, for lying in the spectrum, by the same technique in [5], we are also able to construct solutions to (5). For convenience, we review some notations in [5]:

1) with different parameters

2) with the norm

Theorem 2.5. Assume that with some p > 1 and that, , and for. Let. Then there exist distinct points in such that the following statements are true.

1) For, there exists a unique solution to (5) that continuously depends on, and all solutions have the form

where is a linear combination of functions fo functions, , and is a root of with multiplicity.

2) For, there exists at most one solution to (5), and there exists exactly one solution to (5) when for any.

3) For, there exists at most one solution belonging to, and there exists a unique solution in for any and. All solutions have the form

where is linearly combined by such functions 1 (if) and , , and is a root of with multiplicity.

3. General Vanishing Delays

For a more general vanishing delay, the compactness of the cordial Volterra integral operators is influenced by the value of.

Theorem 3.1. Assume that and that the delay function satisfies the assumptions (D1), (D2), (D3). Then the operator is compact in if and only if.

Proof. From the definition of the function, it is known that. In Lemma 3.6, one obtains from that for all. Hence by Ascoli-Arzela theorem, the compactness of the cordial Volterra integral operator with such a vanishing delay term is shown in Lemma 3.7. The proof will be completed, when the non-compactness of the operator is proved in Lemma 3.8.

The simplest compact condition according to Theorem 3.1 is.

Corollary 3.2. Assume that and that the delay function satisfies the assumptions (D1), (D2), (D3). Then the operator is compact in for any core provided that.

Remark 3.3. Consider the constant core. Then

1), , are non-compact in.

2) For, is compact in.

The existence and uniqueness of solutions to (2) is similar to the classical second kind of VIEs when the corresponding operator is compact.

Theorem 3.4. Assume that and that the delay function sa- tisfies the assumptions (D1), (D2), (D3) and that. Then for all and all, there exists a unique solution to (2).

Proof. In Lemma 3.9, it is shown that the null space of the operator in is, which together with the compactness of implies that the operator has a bounded inverse in (see in [14]). Hence the proof is complete.

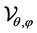
Example 3.5. Consider the following CVIEs with a vanishing delay

1) and for;

2) (the linear form of Lighthill’s equations) and for;

3) and for.

Then the corresponding operators are compact and there exists a unique solution to (2) for and.

Theorems 3.1 and 3.4 are proved by the following lemmas.

Lemma 3.6 Assume that and that is a continuous function in. Then one obtains that for all if .

Proof. In view of

the condition in this lemma yields that for all,

The proof is complete.

Lemma 3.7 Assume that, is a continuous function in I and that. Then is a compact operator in.

Proof. By Ascoli-Arzela theorem, the compactness will be proved by the equiv-continuity of.

Since is a continuous function of and is a continuous function of, for any given there exists an such that

.

Therefore, for with, by Lemma 3.6 and for,

.

In the following, we let and we choose such that for all implies

Therefore,

The proof is complete.

Lemma 3.8. Assume that, and that. Then is a noncompact operator in.

Proof. Without loss of generality, we assume that (or ) for all and suppose that the operator is compact. Then the operator

or

is compact by Lemma 3.7. This contradicts to Corollary 2.3 and the proof is complete.

Lemma 3.9 Assume that, is a continuous function in I and that. Then the null space of is trivial in for all.

Proof. We suppose that and there exists a such that

(6)

Then by

Thus, (6) reduces to

For all and, it holds

Hence (6) yields for sufficiently small and sufficiently large,

This implies that and the proof is complete.

4. Concluding Remarks

In this paper, we consider CVIEs with a vanishing delay:

1) a proportional delay,

2) a nonlinear vanishing delay.

The first case reduces to a classical CVIE with a core limited to a subinterval. Hence these results are trivial from [4] [5]. For case 2), we present the compactness of the operators, i.e.,. In subsequent work, we will investigate the spectrum, eigenvalues and eigenfunctions when and also numerical methods for CVIEs with vanishing delays.

Cite this paper

Wang, H.J., Yang, Z.W. and Khumalo, M. (2017) Cordial Volterra Integral Equations with Vanishing Delays. Journal of Applied Mathematics and Physics, 5, 294-302. https://doi.org/10.4236/jamp.2017.52026

References

NOTES

*This work is supported by the Natural Science Foundation of Heilongjiang Province, China (Grant No. QC2013C019).