ABSTRACT

In this works, by using the modified viscosity approximation method associated with Meir-Keeler contractions, we proved the convergence theorem for solving the fixed point problem of a nonexpansive semigroup and generalized mixed equilibrium problems in Hilbert spaces.

Keywords:

Meir-Keeler Contraction Mappings, Left Regular, Generalized Mixed Equilibrium Problems, Variational Inequalities, α-Inverse Strongly Monotone Mappings, Nonexpansive Semigroups

1. Introduction

As you know, there are many problems that are reduced to find solutions of equilibrium problems which cover variational inequalities, fixed point problems, saddle point problems, complementarity problems as special cases. Equilibrium problem which was first introduced by Blum and Oettli [1] has been extensively studied as effective and powerful tools for a wide class of real world problems, which arises in economics, finance, image reconstruction, ecology, transportation network and related optimization problems.

From now on, we assume that 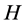is a real Hilbert space with inner product 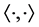and norm, and is a nonempty closed convex subset of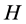. 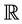is denoted by the set of real numbers. Let 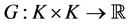be a bifunction. Blum and Oettli [1] consider the equilibrium problem of finding 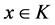such that

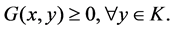(1.1)

The solution set of problem (1.1) is denoted by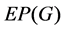, i.e.,

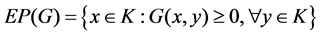
Recently the so-called generalized mixed equilibrium problem has been investigated by many authors [2] [3]. The generalized mixed equilibrium problem is to find 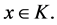such that

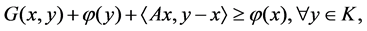(1.2)

where 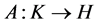is a mapping and 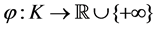is a real valued function. We use 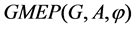to denote the solution set of generalized mixed equilibrium problem i.e.,

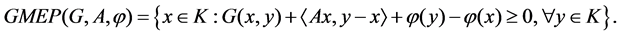
The problem (1.2) is very general in the sense that it includes, as special cases, optimization problems, variational inequality problem, minimax problems, the Nash equilibrium problems in noncooperative games and others (see [4] [5] [6] [7] [8] [9] [10] [11] [12]).

Special Cases: The following problems are the special cases of problem (1.2).

1) If 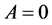then (1.2) is equivalent to finding such that

(1.3)

is called mixed equilibrium problems.

2) If then (1.2) is equivalent to finding such that

(1.4)

is called mixed variational inequality of Browder type [13].

3) If then (1.2) is equivalent to find such that

(1.5)

is called generalized equilibrium problems (shortly, (GEP)). We denote GEP(G,A) the solution set of problem (GEP).

4) If and then (1.2) is equivalent to (1.1).

5) Let for all. Then we see that (1.1) is reduces to the following classical variational inequalities for finding such that

(1.6)

It is known that is a solution to (1.6) if and only if is a fixed point of the mapping, where is a constant and I is an identity mapping.

Let be a mapping from into itself. Let denote the set of fixed points of the mapping T. A mapping is said to be nonexpansive if

A mapping is said to be contractive if there exists a constant such that

A mapping is called -inverse strongly monotone if there exists a constant such that

Remark 1.1 Every -inverse strongly monotone mapping is monotone and -Lipschitz continuous.

In 1967, Halpern [14] introduced the following iterative method for a nonexpansive mapping in a real Hilbert space, for finding and

(1.7)

where and is fixed.

Moudafi [15] introduced the viscosity approximation method for a nonexpansive mapping as follows: For finding and

(1.8)

where and is a contraction mapping.

A viscosity approximation method with Meir-Keeler contraction was first studied by Suzuki [16]. Very recently Petrusel and Yao [17] studied the following viscosity approximation method with a generalized contraction: for finding and

where and is a family of nonexpansive mappings on.

Takahashi and Takahashi [18] introduced the following iterative scheme for solving a generalized equilibrium problems and a fixed point problems of a nonexpansive mapping in a Hilbert spaces: Finding and

(1.9)

where and A is an -inverse strongly monotone mapping. They proved that the sequence generated by (1.9) strongly converges to an element in under suitable conditions.

In this paper, from the recent works [19] [20] [21] [22] [23] [24] [25] [26], we introduced an iterative scheme by the modified viscosity approximation method associated with Meir-Keeler contraction (see [27]) for solving the generalized mixed equilibrium problems and fixed point problem of a nonexpansive semigroup in Hilbert spaces, and also we discussed a convergence theorem. Finally we apply our main results for commutative nonexpansive mappings and semigroup of strongly continuous mappings.

2. Preliminaries

Let be a semigroup and be the Banach space of all bounded real valued functionals on with superimum norm. For each, we define the left and right translation operators and on by and for each and respectively. Let be a subspace of containing 1. An element in the dual space of is said to be a mean on if We denote the value of at the function by. According to the time and circumstances, we write the value by or. It is well known that is a mean of if and only if for each

Let X be a translation invariant subspace of (i.e., and for each) containing 1. Then a mean μ on X is said to be left invariant (resp. right invariant) if (resp.) for each and. A mean μ on X is said to be invariant if μ is both left and right invariant [28] [29]. S is said to be left (resp. right) amenable if X has a left (resp. right) invariant mean. S is amenable if S is left and right amenable [30]. In this case also has an invariant mean. It is known that is amenable when S is commutative semigroup or solvable group. However the free group or semigroup of two generators is not left or right amenable (see [31]). A net of mean on X is said to be left regular if

for each where is the adjoint operator of

Let be a nonempty closed convex subset of. A family is called a nonexpansive semigroup on if for each, the mapping is nonexpansive and for each (see [30] [30]). We denote by the set of common fixed point of, i.e.,

Assume that is a open ball of radius centered at 0 and is a closed convex hull of. For and a mapping, the set of -approximate fixed points of will be denoted by, i.e.,

Lemma 2.1 [32] Let be a function of a semigroup into a Banach space E such that the weak closure of is weakly compact and a subspace of containing all the function with Then for any there exists a unique element in such that for all,

Moreover if is a mean on then

We can write by

Lemma 2.2 [32] Let be a closed convex subset of a Hilbert space H.Let be a nonexpansive semigroup from into itself such that, be a subspace of containing 1, the mapping be an element of for each and and be a mean on. If we write instead of then the following state- ments hold:

1) is a nonexpansive mapping from into,

2) for each

3), for each;

4) if is left invariant then is a nonexpansive retraction from into

Let be a nonempty closed convex subset of a real Hilbert space. Then for any there exists a unique nearest point in, denoted by such that for all,

where is the metric projection of onto. We also know that for and if and only if for all,

A mapping is said to be an -function if for each and for every there exists such that for all. As a consequence, every -function satisfies for each.

Definition 2.3 Let be a metric space. A mapping is said to be a

1) -contraction if is an -function and

for all with

2) Meir-Keeler type mapping if for each there exists such that for each with we have (see [33] [34]).

Theorem 2.4 [34] Let be a complete metric space and is a Meir-Keeler type mapping. Then has a unique fixed point.

Theorem 2.5 [35] Let be a complete metric space and is a mapping. Then the following statements are equivalent.

1) is a Meir-Keeler type mapping;

2) there exists an -function such that is a -con- traction.

Theorem 2.6 [16] Let be a convex subset of a Banach space and let be a Meir-Keeler type mapping. Then for each there exists such that for each with we have

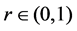
Proposition 2.7 [31] Let be a convex subset of a Banach space, be a nonexpansive mapping on and be a Meir-Keeler type mapping. Then the following statements hold:

1) is a Meir-Keeler type mapping on.

2) For each, the mapping is a Meir- Keeler type mapping on.

Lemma 2.8 [36] Assume that is a sequence of nonnegative real number such that

where is a sequence in and is a sequence in satisfying

1)

2) or

Then

Lemma 2.9 [37] Let and be bounded sequences in a Banach space such that

where is a real sequence in with

If

then

Lemma 2.10 [38] Let for all Suppose that and are sequences in such that

and

for some. Then we have

Lemma 2.11 [39] Let be a nonempty closed convex subset of a real Hilbert space and be a nonexpansive mapping with Then is demiclosed at zero, that is, for all sequence with and it follows that

For solving the equilibrium problem we assume that bifunction satisfies the following conditions:

(A1)

(A2) is monotone, i.e.,

(A3) for each

(A4) for each, is convex and lower semicontinuous.

Lemma 2.12 [1] Let be a nonempty closed convex subset of a real Hilbert space H and G be a bifunction from to satisfying (A1)-(A4). Then for any and, there exists such that

Further, if

then we have the followings:

1) is single-valued;

2) is firmly nonexpansive, i.e., for any

3)

4) is closed and convex.

Lemma 2.13 [18] Let and be as in Lemma 2.12. Then we have

for all and

3. Main Results

Theorem 3.1 Let K be a nonempty closed convex subset of a Hilbert space. Let be a semigroup, be a nonexpansive semigroup on be a bifunction satisfying (A1)-(A4) and be an - inverse strongly monotone mapping with

Let be a proper lower semicontinuous and convex function, X be a left invariant subspace of such that and the function be an element of X for each Let be a left regular sequence of means on X such that as and be a Meir-Keeler contraction. Let be the sequence generated by and

where is bounded sequence in, and are real number sequences in and satisfying the conditions:

(C1)

(C2)

(C3)

(C4)

Then the sequence strongly converges to which is also solves the following variational inequality problem:

(3.1)

Proof. We give the several steps for the proof.

Step 1: First we show that is bounded. Put and for all Then for, we have

(3.2)

Set, then is nonexpansive and. Hence we have

By induction, we can prove that

Hence the sequence is bounded. So and are all bounded.

Step 2: We next show that

Observe that

(3.3)

Indeed

Since is bounded and (3.3) holds. Since and, we have

(3.4)

From and, we have

it follows that

(3.5)

We see that

(3.6)

Combining (3.4) and (3.5) with (3.6), we obtain

Using Lemma 2.13, (3.3),(C1) and (C4), then we have

From this inequality and (C3), it follows from Lemma 2.9 that

(3.7)

It implies that

(3.8)

Step 3: Next we prove that for all,

Put

Set It is easily seen that D is a nonempty bounded closed convex subset of K. Further and are in D. To complete our proof, we follows that proof line as in [30]. From [40], for every there exists such that for all,

(3.9)

From Corollary 1.1 in [40], there exists a natural number such that for all

(3.10)

Since is left regular, for there exists such that

for all Therefore, we have for all

(3.11)

We observe from Lemma 2.2 (iii) that

(3.12)

Combining (3.10), (3.12) and (3.12), we have for all

(3.13)

Let and. Then there exists which satisfies (3.9). From (C3) there exist such that. From (3.7) there exists

such that and for all So from (3.9) and (3.13), we have

Hence Since is arbitrary,

Step 4: We next show that

(3.14)

Using inequality (3.2), we obtain

(3.15)

which implies that

From (C1)-(C4) and (3.8), we obtain

(3.16)

Since is firmly nonexpansive,

Therefore

Then we have

which yields

Hence, from (C2), (C3) and (3.16) we obtain

(3.17)

Since we have and hence

(3.18)

On the other hand, by Proposition 2.7 (i), we know that is a Meir-Keeler contraction. From Theorem 2.4, there exists a unique element such that which is equivalent to

Step 5: We next show that

To see this, we chose a subsequence of such that

Since is a bounded, K is closed and H is reflexive, there exists a point such that. From (3.17) and (3.18) there exists a corresponding subsequence of (resp. of) such that (resp.). We next show that Since We can write

From (A2), we have

Then

(3.19)

Put for and. Since and, . So from (3.19) we have

From (A4), we have

(3.20)

From (A1)-(A4) and (3.20), we have

It follows that

letting by (A3), we have

Hence It is easily seen that Indeed, since and for all we conclude from Lemma 2.1 that. Consequently, we have and hence

(3.21)

Step 6: Now we are in a position to show that is a fixed point of.

Let. Then we have

We note that

and

It follows from Lemma 2.10 that

(3.22)

On the other hand, we have

It follows from (3.17) and (3.22) that

(3.23)

Therefore Let be an another subsequence of converging to with. Similarly, we can find. Hence we have

This is a contradiction. Hence we have

Step 7: We finally show that as.

Suppose that does not strongly converge to. Then there exists and a subsequence of such that for all By Proposition 2.7, for this there exists such that

So we have

This implies that

Hence

Using (3.21) and (C2), we can conclude by Lemma 2.8 that as . This is a contradiction and hence the sequence converges to . Thus we completes the proof.

Acknowledgements

This work was supported by the Basic Science Research Program through the National Research Foundation(NRF) Grant funded by Ministry of Education of the republic of Korea(2015R1D1A1A09058177).

Cite this paper

Kim, J.K., Salahuddin and Lim, W.H. (2017) An Iterative Algorithm for Generalized Mixed Equilibrium Problems and Fixed Points of Nonexpansive Semigroups. Journal of Applied Mathematics and Physics, 5, 276-293. https://doi.org/10.4236/jamp.2017.52025

References