Journal of Applied Mathematics and Physics
Vol.05 No.02(2017), Article ID:74146,9 pages
10.4236/jamp.2017.52024
Application of Hypergeometric Series in the Inverse Moments of Special Discrete Distribution*
Hongyu Bao, Wuyungaowa
Department of Mathematics, College of Sciences and Technology, Inner Mongolia University, Huhhot, China




Received: December 29, 2016; Accepted: February 12, 2017; Published: February 15, 2017
ABSTRACT
In this paper, we use the generalized hypergeometric series method the high- order inverse moments and high-order inverse factorial moments of the generalized geometric distribution, the Katz distribution, the Lagrangian Katz distribution, generalized Polya-Eggenberger distribution of the first kind and so on.
Keywords:
Hypergeometric Series, Inverse Moments, Factorial Inverse Moments

1. Introduction
The moment is one of the most widely used features of probability of random variables. The moments of random variables have been widely used in many important fields such as finance, probability theory, statistics and so on. So the calculation of the moment is very important. The inverse moment is a hot research direction in recent years. Inverse moment plays an important role in risk assessment, insurance and finance, and it is an important concept in probability. The study of the inverse moments originates from random sampling,  is the
is the
number of observations 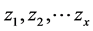 with mean
with mean 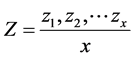 if
if
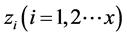 is independent and identically distributed random variable, the variance is
is independent and identically distributed random variable, the variance is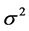 ,when
,when 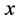 is a constant, the variance of
is a constant, the variance of 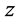 is
is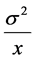 , but when the
, but when the 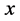 is a random variable, the variance of
is a random variable, the variance of  was
was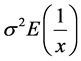 , at this point in the
, at this point in the
sampling problem of inverse moment are introduced. Generally, the distribution of 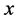 is mainly the Poisson distribution, binomial distribution and so on.
is mainly the Poisson distribution, binomial distribution and so on.
The research on inverse moments of the binomial distribution and the Poisson distribution has been a long history. In 1945, Frederick F. Stephan studied the inverse moments of first and second order of the binomial distribution (see [1]). Grab and Stephan calculated tables of reciprocals for binomial and Poisson distribution as well as derive a recurrence relation. They also derived an exact expression for the first inverse moment (see [2]). Govindarajulu in 1963 a recursive formula moments of binomial distribution has been obtained (see [3]). In 1972, Chao and Strawderman (see [4]) considered slightly different inverse mo-
ments defined as 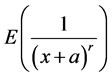 which are frequently easier to calculate.
which are frequently easier to calculate.
At present, more and more scholars are interested in the study of inverse moment, and have a wealth of research results mainly binomial distribution, Poisson distribution, negative binomial distribution, logarithmic distribution (see [5]). In this paper describes the use of generalized hypergeometric series inverse moments and factorial inverse moment distribution of some. It mainly includes Janardan discussed the distribution of the generalized Polya-Eggenberger distribution of the first kind, and the special value of the parameters (see [6]).
In the next, we will give some definitions necessarily.
Definition 1: Suppose X is a generalized geometric random variable with parameters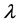 , having probability mass function
, having probability mass function
 (1)
(1)
where 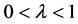
Definition 2: Suppose X is a generalized Polya-Eggenberger of the first kind random variable with parameters 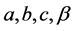 having probability mass function
having probability mass function
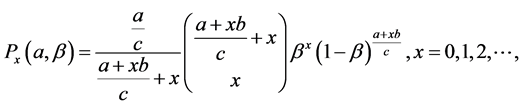 (2)
(2)
where
Definition 3: Suppose X is a Katz random variable with parameters 

where
Definition 4: Suppose X is a Lagrangian Katz random variable with parameters 

where
The definition of generalized hypergeometric series:
where
If 

2. The Inverse Moments of Some Discrete Distributions
In this section, we use a generalized hypergeometric series to obtain the inverse moments of some discrete distributions.
Theorem 2.1: Suppose 



where
Proof. By definition 1, then
Note: when
Theorem 2.2: Suppose 



where
Proof. By definition 2, then
Note: when
Let 
Let 
Let 
Let 
Corollary 2.1: Suppose



where
Proof. Let 
Note: when
Corollary 2.2: Suppose 


where
Proof. Let 
Note: when
3. The Factorial Inverse Moments of Some Discrete Distributions
In this section, we use generalized hypergeometric series to obtain the inverse factorial moments of some discrete distributions.
Theorem 3.1: Suppose 



where
Proof. By definition 1, then
Note: when
Theorem 3.2: Suppose 



where
Proof. By definition 2, then
Note: when
Let 
Let 
Let 
Let 
Corollary 3.1: Suppose 



where
Proof. Let 
Note: when
Corollary 3.2: Suppose 



where
Proof. Let 
Note: when
Cite this paper
Bao, H.Y. and Wuyungaowa (2017) Application of Hyper- geometric Series in the Inverse Moments of Special Discrete Distribution. Journal of Applied Mathematics and Physics, 5, 267- 275. https://doi.org/10.4236/jamp.2017.52024
References
- 1. Stephan, F.F. (1945) The Expected Value and Variance of the Reciprocal and Other Negative Powers of a Positive Bernoulli Variate. Annals of Mathematical Statistics, 16, 50-61. https://doi.org/10.1214/aoms/1177731170
- 2. Grab, E.L. and Savage, I.R. (1954) Tables of the Expected of 1/x for Positive Bernoulli and Poisson Variable. Journal of American Statistical Association, 49, 167-177.
- 3. Govindarajulu, Z. Recurrence Relation for the Inverse Moments of the Positive Binomial Variable. Journal of American Statistical Association, 58, 468-473. https://doi.org/10.1080/01621459.1963.10500859
- 4. Chao, M.T. and Strawderman, W.E. (1972) Negative Moments of Positive Random Variables. Journal of the American Statistical Association, 67, 429-431. https://doi.org/10.1080/01621459.1972.10482404
- 5. Wang, C.Y. and Wuyungaowa (2015) Recurrence Relation and Accurate Value on Inverse Mo-ment of Discrete Distributions. Journal of Probability and Statistics. https://doi.org/10.1155/2015/972035
- 6. Znidaric, M. (2005) Asymptotic Expansion for Inverse Moments of Binomial and Poisson Distribution. Statistics Theory [math.ST].
NOTES
*Funded projects: The research is supported by the National Natural Science Foundation of China under Grant.














































