ABSTRACT

A large number of problems in engineering can be formulated as the optimization of certain functionals. In this paper, we present an algorithm that uses the augmented Lagrangian methods for finding numerical solutions to engineering problems. These engineering problems are described by differential equations with boundary values and are formulated as optimization of some functionals. The algorithm achieves its simplicity and versatility by choosing linear equality relations recursively for the augmented Lagrangian associated with an optimization problem. We demonstrate the formulation of an optimization functional for a 4th order nonlinear differential equation with boundary values. We also derive the associated augmented Lagrangian for this 4th order differential equation. Numerical test results are included that match up with well-established experimental outcomes. These numerical results indicate that the new algorithm is fully capable of producing accurate and stable solutions to differential equations.

Keywords:

Augmented Lagrangian Methods, Method of Multipliers, Finite Element Solutions, Differential Equations

1. Introduction

Many problems in engineering are described by boundary value problems of differential equations of order 2k in the form of

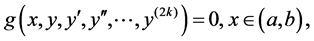(1)

subject to certain boundary conditions, where 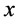is the independent variable in interval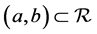, 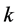is a positive integer, 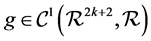, and 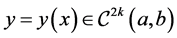is a solution to (1). Such a solution is also referred to as a strong solution because of the requirement that.

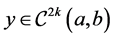However, a strong solution to (1) may not exist for some problems. Even when a strong solution to (1) exists, such a solution may be too costly to calculate numerically in practice.

Therefore, weak formulations of (1) are preferred. Assume that (1) admits a weak formulation in the following form.

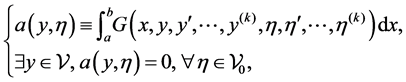(2)

where is usually a subset of the Hilbert space 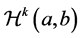subject to some boundary conditions, 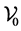is a subspace of 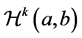satisfying some homogeneous boundary conditions, and. In other words, a solution to (1) also satisfies (2).

A solution to (2) is referred to as a weak solution to (1) because of 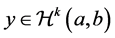instead of.

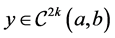We also assume that for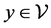, there exists a certain functional

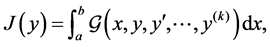(3)

where such that a stationary point of functional satisfies (2). A stationary point of (3) satisfies

(4)

where is referred to as a test function. Equivalently, a stationary point of (3) satisfies

(5)

Refer to [1] for more details.

We see that a weak solution of (1) corresponds to an optimization problem of functional defined in (3). Such a weak solution is simply a stationary point of (3).

As pointed out in [1], a boundary value problem of inhomogeneous boundary conditions can be effectively treated as a problem with homogeneous boundary conditions by introducing a special function satisfying the inhomogeneous boundary conditions. For simplicity, we will assume homogeneous boundary conditions for the rest of this paper. Under this assumption,

(6)

Hestenes [2] and Powell [3] introduced the augmented Lagrangian methods or the method of multipliers in 1969 for the study of optimization problems. Comprehensive applications of augmented Lagrangian methods for optimization and boundary value problems were investigated by Bertsekas [4], Fortin and Glowinski [5].

Even though most research on the augmented Lagrangian methods have been focusing on their direct applications in optimization, there have been consistent interests in using the augmented Lagrangian methods in other fields over the years. Recent applications of the augmented Lagrangian methods include image processing and computer vision [6], numerical solutions to Laplace equation with various boundary values [7], mechanics [7] [8] [9], medical imaging and computational biology [10], geophysics [11], ontology regarding big data representation and storage [12], and elastica theory [13], to name just a few.

In this paper, we’ll investigate the applications of the augmented Lagrangian methods in boundary value problems of differential equations associated with problems from engineering. These are usually higher order differential equations (4th or higher). The feature of higher order of these problems is exploited to allow the development of simple and stable methods for their numerical solutions using finite elements.

The rest of the paper is organized in the following way. In section 2, we briefly review the augmented Lagrangian methods for optimization problems, and the finite element methods for solving weak formulation (2). In section 3, we’ll introduce a special formulation for the construction of an augmented Lagrangian for finding numerical solutions to higher order differential equations using finite elements. We show a sample boundary value problem of a higher order nonlinear differential equation, its weak formulation, and the associated optimization problem in section 4. We’ll present numerical tests for this sample differential equation in section 5. The numerical results demonstrate that this new version of the augmented Lagrangian methods is accurate, stable, versatile, and easy to implement.

2. Augmented Lagrangian Methods and Finite Element Solutions

Generally speaking, an analytic solution to an optimization problem is not available. We therefore focus on numerical solutions using augmented Lagrangian methods and finite elements.

2.1. Augmented Lagrangian Methods

For a constrained optimization problem

(7)

where is a subset of the set of all natural numbers, and is some functional space, an augmented Lagrangian method for (7) introduces an associated augmented Lagrangian

(8)

and the associated unconstrained optimization problem

(9)

where for each, is a Lagrangian multiplier, and is a pre-chosen constant serving as a penalty when is not sufficiently small.

Notice that the function spaces in (7) and (9) are identical. In particular, both (7) and (9) impose the same regularity requirements on through.

When an optimization problem is associated with a boundary value problem of a differential equation, we have the leeway for constructing the associated augmented Lagrangian that imposes weaker regularity requirements than those of the original optimization problem. We’ll present the formulation later in a separate section.

2.2. Finite Element Methods

Assume that is a -dimensional subspace that approximates in (2). Assume also that is a basis for. The Galerkin method of finite elements amounts to finding a function such that

(10)

where is defined in (2).

Because is finite dimensional, there exist unique coefficients such that

(11)

Because (10) is true for all, it must be true for every.

(12)

In fact, (12) forms a system of equations for unknown coefficients. These equations are linear or nonlinear depending on being linear or nonlinear. Finding an approximate solution to (2) corresponds to solving the system of Equations (12) for coefficients.

In particular, because, it is required that for. Such regularity requirement may become too demanding on the basis for when is big.

Using weaker regularity requirements generally results in the following advan- tages.

1) We may use simpler test function that improves overall numerical efficiency.

2) The condition numbers for linearized matrices of (12) are much smaller [1].

Our goal is to find new approaches that use the least regularity requirement possible, to be introduced next.

3. Augmented Lagrangian Methods for Differential Equations

In this section, we propose a new approach for the construction of augmented Lagrangian associated with boundary value problems of differential equations. This new approach exploits the feature of higher order of the differential equations to arrive at the least regularity requirements on weak solutions to boundary value problems. The approach coincides with those discussed in [5] for differential equations of second order or less.

Recall that to find a weak solution to (1) means to solve for in (5). That means all test functions must be from. We now propose the following augmented Lagrangian associated with (3).

(13)

where, is a certain subspace of that is associated with some of the homogeneous boundary conditions of (1) (see assumption for (6)), are supplementary variables to be linked to by the recursive linear equality relations

(14)

and, are Lagrangian multipliers, which are also functions of, and are pre-chosen constants serving as penalty in case any of the linear equality relations in (14) is not met satisfactorily.

We immediately recognize the major difference between functional of (3) and the augmented Lagrangian of (13). Whereas the regularity requirement for of (3) is

(15)

the regularity requirements for augmented Lagrangian of (13) are

(16)

independent of, the order of the differential equation.

The following is the major conclusion of this paper.

Theorem 3.1 If is a stationary point of (13) where, then satisfies (14), and is a weak solution to of (3), which is also a weak solution to (1).

Proof. A stationary point for the augmented Lagrangian of (13) satisfies,

(17)

(18)

(19)

(20)

where, for, , for, are the respective test functions.

The four stationary point relations (17), (18), (19) and (20) expand into

(21)

(22)

(23)

(24)

Because (24) is true for any for, it proves that satisfies the recursive linear equality relations (14). That is,

(25)

in weak sense, implying that.

Consequently, (21), (22) and (23) reduce to

(26)

(27)

(28)

for any test functions, for,.

, if we choose functions and for in the following ways,

then (26), (27) and (28) become

(29)

(30)

(31)

After adding up all equations in (29), (30) and (31), we arrive at

(32)

Using results in (25) along with (32), we have proved that satisfies (5) for any test function. That completes the proof.

We therefore have three approaches for finding approximate solutions to (1).

1) Solve (1) for an approximate strong solution in directly, e.g., by a certain finite difference method. This approach demands the highest regularity requirement where functions involved must belong to.

2) Solve (1) for an approximate weak solution in via (2), (10) and (12). This approach demands that functions involved belong to. This has been the standard approach found in most work related to finite element methods.

3) Solve (1) for an approximate weak solution in by finding stationary point of the augmented Lagrangian (13). This approach demands that functions involved belong to, regardless of the order of differential Equation (1). This approach achieves the minimum regularity requirement possible for any differential equation of order second or higher.

The method that uses the augmented Lagrangian (13) has the least regularity requirement among the three approaches.

Regardless of the order of differential Equation (1), finding approximate solution using the augmented Lagrangian (13) with finite elements is simple and standard as illustrated below.

・ Because of (16), we can always use Hermite cubic polynomials to approximate, and use piecewise linear functions to approximate and.

・ The bases for the corresponding finite dimensional spaces for finite elements are the Hermite cubic shape functions and linear shape functions, respectively.

・ The approximate solutions are obtained from (12) by substituting Hermite cubic shape functions and linear shape functions for, respectively.

We’ll implement the augmented Lagrangian methods associated with Lagrangian (13) for finding approximate solution to a boundary value problem of a 4th order nonlinear differential equation in the next section.

4. A Sample Differential Equation

Many of the problems in engineering are described by boundary value problems of differential equations of orders two or higher. An example is the following nonlinear Euler-Bernoulli beam equation [14] [15] [16],

(33)

with various boundary conditions (natural boundary conditions are not enforced by standard arguments), such as:

(34)

for a rectangular beam of length L, width and thickness. Here, is the deflection of the beam, E Young’s modulus, I moment of inertia of cross-section of the beam, represents residual force which is independent of,

(35)

represents the axial force in the beam, and is the intensity of external force exerted on the beam which is assumed to be continuous in. We see that (33) along with (34) is just a special case of (1) for. A strong solution of (33) requires that.

Subspace associated with (33) becomes

(36)

Because boundary conditions in (34) are themselves homogeneous, the subspace of all test functions is identical to, as has been assumed back in (6).

When multiplying any test function to (33), integrating the result over, and applying integration by parts, we arrive at the following.

(37)

In other words, a solution to (33) also satisfies (37).

To find a solution to (33) becomes to find a function such that (37) is true. A solution to (37) is therefore called a weak solution to (33) because the regularity requirement has become

(38)

We also call (37) the weak formulation of (33).

Furthermore, for any, if we define

(39)

where, we can verify with some algebraic manipulations that a stationary point of in (39) is a weak solution to (33). Details are omitted here for brevity.

We’ve shown that (33) indeed admits a weak formulation (37). A weak solution of (33) corresponds to a stationary point of (39). Such a stationary point is a solution to an optimization problem of functional of (39).

Based on functional in (39), we can define the associated augmented Lagrangian as shown below.

(40)

where,

(41)

and

(42)

A stationary point of (40) hence satisfies the following five equations.

(43)

for their respective test functions

(44)

and

(45)

Notice that boundary conditions (34) become

(46)

and

(47)

Finding an exact solution to a stationary point from (43) is highly unlikely, if not impossible. Fortin and Glowinski [5] suggested an iterative algorithm (called ALG1) for finding approximate solution to (43) as shown below.

Steps of ALG1.

1) Choose arbitrary initial guesses and.

2) For, calculate by solving

(48)

where test functions, and satisfy (44), then update by

(49)

where and are two pre-chosen positive constants.

3) Check for convergence. Repeat step 2 when needed. Convergence is reached when the following conditions are met,

(50)

for a pre-chosen relative tolerance.

It seems that (48) is just as difficult to solve as (43) is. Fortin and Glowinski [5] suggested yet another iterative algorithm (called ALG2) for finding approximate solution to (48) as shown below.

Steps of ALG2.

1) For a fixed, let,.

2) For,

a), solve (51) for,

(51)

subject to boundary conditions (46).

b), , solve system of Equations (52) for and,

(52)

subject to boundary conditions (47).

3) Repeat step 2 for a certain number of times, or until convergence. Then

(53)

In particular, we solve (51) and (52) using the standard finite element approach where we approximate and by the Hermit cubic polynomials, and approximate, and by piecewise linear functions.

We’ll present numerical results from solving (33) using ALG1 and ALG2 in the next section.

5. Numerical Tests

In this section, we study a microbeam switch that is electrostatically actuated by an applied voltage. Hu, Chang and Huang [17] first studied such a problem in 2004. The structure [17] can be schematically described as a thin metal beam hanging over a substrate separated by some insulator, where one end of the microbeam is fixed and the other is free (fixed-free beam). The beam is pulled (deflected) towards the substrate when a voltage is applied between the beam and the substrate. The action of such a structure is modelled using (33) subject to boundary conditions (34). We are interested in the gap between the free end of the microbeam and the substrate subject to different applied voltages.

The specifics of the microbeam structure are listed below.

・ Beam length, width and thickness are 20 mm, 5 mm and 57 µm, respectively.

・ Initial gap between microbeam and substrate is 92 µm.

・ Young’s modulus is 1.558 × 10¹¹ Pa.

・ Permittivity of vacuum is 8.85 × 10⁻¹² F/m.

・ Poisson’s ratio of 0.06 is used because the microbeam is considered wide, i.e., width is significantly greater than thickness.

We present in Table 1 numerical results from solving (33) subject to boundary conditions (34). Our numerical results indicated that the newly introduced augmented Lagrangian methods (ALM) are fully capable of producing quality solutions that match up well with experiment data. The number of finite elements used is denoted by in Table 1.

The relative errors of results obtained from ALM are comparable to those in [17] and [16], for all cases of finite element approximations. In fact, it appears

that the augmented Lagrangian methods have already converged with relatively small number (i.e., 12) of finite elements because increasing the number of finite elements used does not cause much of a change in accuracy.

6. Conclusion

An algorithm is developed based on the augmented Lagrangian methods and the finite element, exploiting the order of the differential equation it solves. Independent of the order of the differential equation, we are always able to use only Hermite cubic and linear finite elements to approximate variables involved. As a result, this algorithm is easy to implement, and is capable of producing accurate and stable solutions to engineering problems that admit weak formulations associated with optimization of some functionals. Extensions of this algorithm for solving engineering problems described by higher order partial differential equations are being investigated by the author. Results will be submitted for publication in the near future.

Cite this paper

Li, X.F. (2017) Augmented Lagrangian Methods for Numerical Solutions to Higher Order Differential Equations. Journal of Applied Mathematics and Physics, 5, 239-251. https://doi.org/10.4236/jamp.2017.52021

References