Energy and Power En gi neering, 2011, 3, 478-482
doi:10.4236/epe.2011.34057 Published Online September 2011 (http://www.SciRP.org/journal/epe)
Analysis of Chaoti c Fe rroresonance Phenomena in
Unloaded Transformers Including MOV
Ataollah Abbasi1, Mehrdad Rostami1, Ahmad Gholami 2, Hamid R. Abbasi2
1Shahed University, Tehran, Iran
2Iran University of Science and Technology, Tehran, Iran
Received June 5, 2011; revised July 15, 2011; accepted July 23, 2011
Abstract
We study the effect of a parallel metal oxide surge arrester on the ferroresonance oscillations of transformers.
It is expected that the arresters generally cause ferroresonance drop out. Simulation has been done on a three
phase power transformer with one open phase. Effect of varying input voltage is studied. The simulation re-
sults reveal that connecting the arrester to transformers poles, exhibits a great mitigating effect on ferroreso-
nant over voltages. Phase plane along with bifurcation diagrams are also presented. Significant effect on the
onset of chaos, the range of parameter values that may lead to chaos and magnitude of ferroresonant voltages
is obtained, shown and tabulated.
Keywords: Power Transformer, Phase Plane Diagram, Bifurcation Diagram, Chaotic Ferroresonance
1. Introduction
Ferroresonance is a complex nonlinear electrical phe-
nomenon that can cause dielectric & thermal problems to
components power system. Electrical systems exhibiting
ferroresonant behaviour are categorized as nonlinear
dynamical systems. Therefore conventional linear solu-
tions cannot be applied to study ferroresonance. The pre-
diction of ferroresonance is achieved by detailed model-
ing using a digital computer transient analysis program
[1]. Ferroresonance should not be confused with linear
resonance that occurs when inductive and capacitive re-
actance of circuit is equal. In linear resonance the current
and voltage are linearly related and are frequency de-
pendent. In the case of ferroresonance it is characterized
by a sudden jump of voltage or current from one stable
operating state to another one. The relationship between
voltage and current is depends not only on frequency but
also on other factors such as system voltage magnitude,
initial magnetic flux condition of transformer iron core,
total loss in the ferroresonant circuit and moment of
switching [2].
Ferroresonance may be initiated by contingency swi-
tching operation, routine switching, or load shedding
involving a high voltage transmission line. It can result
in Unpredictable over voltages and high currents. The
prerequisite for ferroresonance is a circuit containing
iron core inductance and a capacitance. Such a circuit is
characterized by simultaneous existence of several stea d y-
state solutions for a given set of circuit parameters. The
abrupt transition or jump from one steady state to another
is triggered by a disturbance, switching action or a grad-
ual change in values of a parameter. Typical cases of
ferroresonance are reported in [1-4]. Theory of nonlinear
dynamics has been found to provide deeper insight into
the phenomenon. [5-8] are among the early investiga-
tions in applying theory of bifurcation and chaos to fer-
roresonance. The susceptibility of a ferroresonant circuit
to a quasi-periodic and frequency locked oscillations are
presented in [9,10]. Th e effect o f in itial cond ition s is also
investigated. The effect of transformer modeling on the
predicted ferroresonance oscillations is studied in [11].
Using a linear model, authors of [12] have indicated the
effect of core loss in damping ferroresonance oscillations.
The importance of treating core loss as a nonlinear func -
tion of voltage is highlighted in [7]. An algorithm for
calculating core loss from no-load characteristics is given
in [13]. Evaluation of chaos in voltage transformer, ef-
fect of resistance of key on the chaotic behavior voltage
transformer and subharmonics that produced with fer-
roresonance in this type tran sformer and quantification of
the chaotic behavior of ferroresonant v oltage transformer
circuits are studied in [9,14,15].

A. ABBASI ET AL.479
2. System Modeling
Transformer is assumed to be connected to the Power
System while one of the three switches are open and only
two phases of it are energized, which produces induced
voltage in the open phase. This voltage, back feeds the
distribution line. Ferroresonance will occur if the distri-
bution line is highly capacitive. System involves the
nonlinear magnetizing reactance of the transformer’s
open phase and resulted shunt and series capacitance of
the distribution line.
Base system model is adopted fro m [3] with the MOV
arrester connected across the transformer winding which
is showed in Figure 1 Linear approximation of the peak
current of the magnetization reactance can be presented
by Equation (1):
l
ia

 (1)
However, for very high currents, the iron core might
be saturated where the flux-current characteristic be-
comes highly nonlinear. The l i

 characteristic of the
transformer can be demonstrated by the polynomial in
Equation (2):
q
l
ia b

  (2)
Arrester can be expressed by the Equation (3):
VKI

 (3)
V represents resistive voltage drop, I represents ar-
rester current and K is constant and

is nonlinearity
constant. The differential Equatio n for the circuit in Fig-
ure 1 can be derived as follows:


21
cos
1sign
q
p
Etp ab
RC C
pp
CK



 











(4)
where d pdt  and

represents the power frequency
and E is the peak value of the voltage source, shown in
Figure 1.
Figure 1. Circuit of system.
Presenting in the form of state space Equations,

and p

will be state variables as follows:
1
,2
x
px



 (5)
12
x
x

 (6)


2
21
22
1
cos
1
q
x1
x
Etax bx
RC C
xsign x
CK













(7)
3. Simulation Results
Typical values for various system parameters considered
for simulation are as giv en below [5]:
0.0005
50
0.001
70
0.0072
11 0.0028;
b
qa
b
qa
b
qa















1 p. u.,100 p.u.,0.047 p.u.
0 - 6 p.u.,2.501,25.
RC
EK





Initial conditions:


00,01.44 p.u.p  
Table 1 shows different values of E, considered for
analyzing the circuit in absence of surge arrester.
Table 2 includes the set of cases which are considered
for analyzing the circuit including arrester:
Time domain simulations were performed using the
MATLAB programs which are similar to EMTP simula-
tion [3]. For cases including arrester, it can be seen that
Table 1. (a) Behaviour of system without MOV for E = 1, 2,
3. (b) Behaviour of system without MOV for E = 4, 5, 6.
(a)
E
q 1 2 3
5 Priodic Priodic Priodic
7 Priodic Priodic Chaotic
11 Priodic Priodic Chaotic
(b)
E
q 4 5 6
5 Chaotic Chaotic Chaotic
7 Chaotic Chaotic Chaotic
11 Chaotic Chaotic Chaotic

A. ABBASI ET AL. 480
Table 2. (a) Behaviour of system with MOV for E = 1, 2, 3.
(b) Behaviour of system with MOV for E = 4, 5, 6.
(a)
E
q 1 2 3
5 Priodic Priodic Priodic
7 Priodic Priodic Priodic
11 Priodic Chaotic Priodic
(b)
E
q 4 5 6
5 Priodic Priodic Priodic
7 Priodic Priodic Chaotic
11 Chaotic Chaotic Chaotic
ferroresonant drop out will be occurred.
Figure 2 show the phase plane plot of system states
without arrester for E = 1 p.u.
Figure 3 shows the phase plane plot and time domain
simulation of system states without arrester fo r E = 4 p.u.
which depicts chaotic behavior and Figure 4 shows the
corresponding time domain wave form.
Also Figures 5-7 show the bifurcation diagram of cha-
otic behaviours for three of values of q. The system
shows a greater tendency for chaos for saturation char-
acteristics with lower knee points, which corresponds to
higher values of expon ent q.
Figure 2. Phase plane diagram for E = 1, q = 11 without
MOV.
Figure 3. Phase plane diagram for E = 4, q = 11 without
MOV.
Figure 4. Time domain chaotic wave form for E = 4, q = 11
without MOV.
Figure 5. Bifurcation diagram for q = without MOV.
Figure 6. Bifurcation diagram for q = 7 without MOV.
Figure 7. Bifurcation diagram for q = 11 without MOV.
Figures 8-10 show that chaotic region mitigates by
applying MOV surge arrester. Tendency to chaos exhib-
ited by the system increases while q increases too.
With consideration to Figures 8-10 MOV makes a
mitigation in ferroresonance chaoti c behavior in transfor-
mer that in down value of q the chaotic region are

A. ABBASI ET AL.481
Figure 8. Bifurcation diagram for q = 5 with MOV.
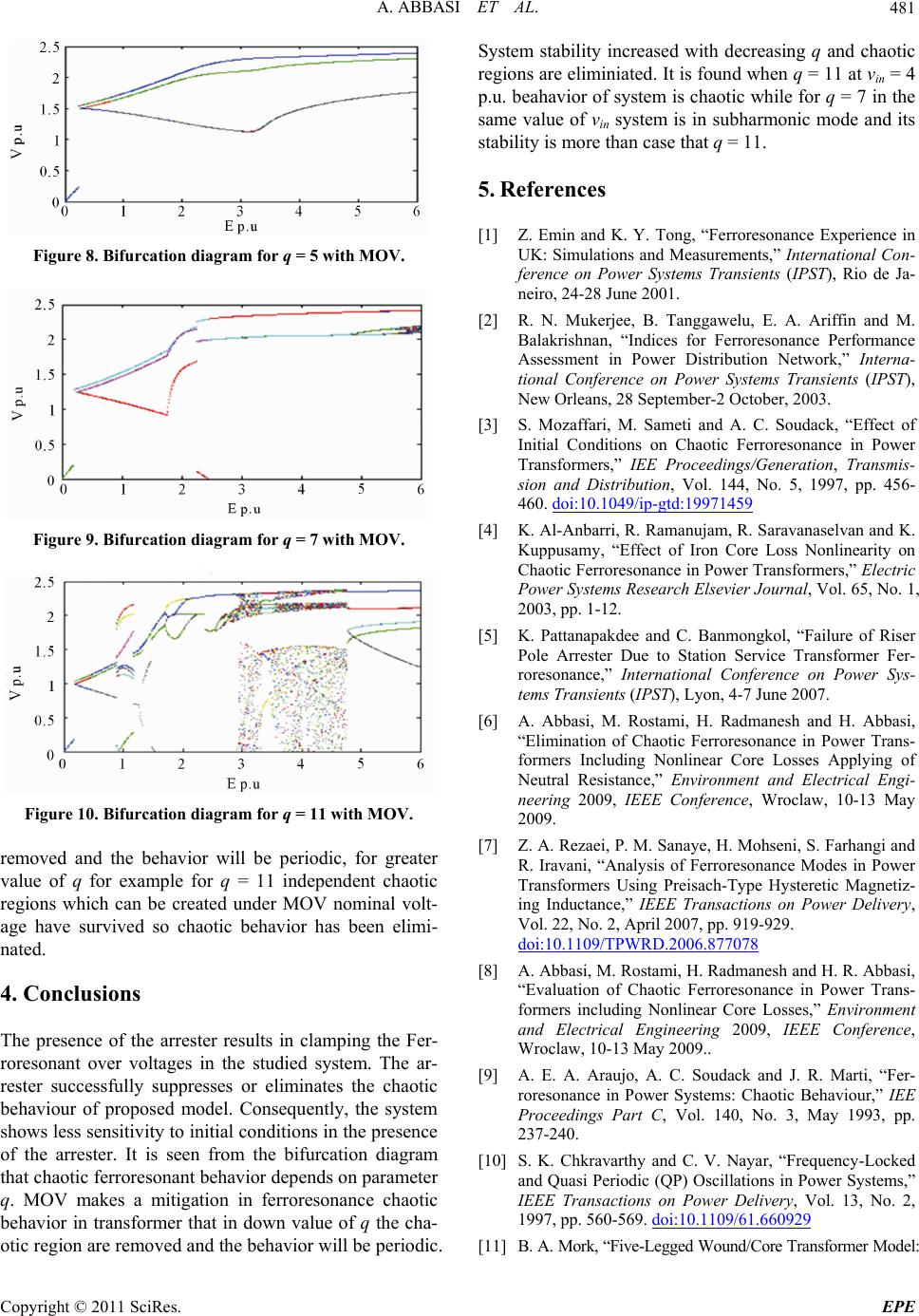
Figure 9. Bifurcation diagram for q = 7 with MOV.
Figure 10. Bifurcation diagram for q = 11 with MOV.
removed and the behavior will be periodic, for greater
value of q for example for q = 11 independent chaotic
regions which can be created under MOV nominal volt-
age have survived so chaotic behavior has been elimi-
nated.
4. Conclusions
The presence of the arrester results in clamping the Fer-
roresonant over voltages in the studied system. The ar-
rester successfully suppresses or eliminates the chaotic
behaviour of proposed model. Consequently, the system
shows less sensitivity to initi al conditions in th e presence
of the arrester. It is seen from the bifurcation diagram
that chaotic ferroresonant behavior depends on parameter
q. MOV makes a mitigation in ferroresonance chaotic
behavior in transformer that in down value of q the cha-
otic region are removed and the behavior will be periodic.
System stability increased with decreasing q and chaotic
regions are eliminiated. It is found when q = 11 at vin = 4
p.u. beahavior of system is chaotic while for q = 7 in the
same value of vin system is in subharmonic mode and its
stability is more than case that q = 11.
5. References
[1] Z. Emin and K. Y. Tong, “Ferroresonance Experience in
UK: Simulations and Measurements,” International Con-
ference on Power Systems Transients (IPST), Rio de Ja-
neiro, 24-28 June 2001.
[2] R. N. Mukerjee, B. Tanggawelu, E. A. Ariffin and M.
Balakrishnan, “Indices for Ferroresonance Performance
Assessment in Power Distribution Network,” Interna-
tional Conference on Power Systems Transients (IPST),
New Orleans, 28 September-2 October, 2003.
[3] S. Mozaffari, M. Sameti and A. C. Soudack, “Effect of
Initial Conditions on Chaotic Ferroresonance in Power
Transformers,” IEE Proceedings/Generation, Transmis-
sion and Distribution, Vol. 144, No. 5, 1997, pp. 456-
460. doi:10.1049/ip-gtd:19971459
[4] K. Al-Anbarri, R. Ramanujam, R. Saravanaselvan and K.
Kuppusamy, “Effect of Iron Core Loss Nonlinearity on
Chaotic Ferroresonance in Power Transformers,” Electric
Power Systems Research Elsevier Journal, Vol. 65, No. 1,
2003, pp. 1-12.
[5] K. Pattanapakdee and C. Banmongkol, “Failure of Riser
Pole Arrester Due to Station Service Transformer Fer-
roresonance,” International Conference on Power Sys-
tems Transients (IPST), Lyon, 4-7 June 2007.
[6] A. Abbasi, M. Rostami, H. Radmanesh and H. Abbasi,
“Elimination of Chaotic Ferroresonance in Power Trans-
formers Including Nonlinear Core Losses Applying of
Neutral Resistance,” Environment and Electrical Engi-
neering 2009, IEEE Conference, Wroclaw, 10-13 May
2009.
[7] Z. A. Rezaei, P. M. Sanay e, H. Mohseni, S. Farhangi an d
R. Iravani, “Analysis of Ferroresonance Modes in Power
Transformers Using Preisach-Type Hysteretic Magnetiz-
ing Inductance,” IEEE Transactions on Power Delivery,
Vol. 22, No. 2, April 2007, pp. 919-929.
doi:10.1109/TPWRD.2006.877078
[8] A. Abbasi, M. Rostami, H. Radmanesh and H. R. Abbasi,
“Evaluation of Chaotic Ferroresonance in Power Trans-
formers including Nonlinear Core Losses,” Environment
and Electrical Engineering 2009, IEEE Conference,
Wroclaw, 10-13 May 2009..
[9] A. E. A. Araujo, A. C. Soudack and J. R. Marti, “Fer-
roresonance in Power Systems: Chaotic Behaviour,” IEE
Proceedings Part C, Vol. 140, No. 3, May 1993, pp.
237-240.
[10] S. K. Chkravarthy and C. V. Nayar, “Frequency-Locked
and Quasi Periodic (QP) Oscillations in Power Systems,”
IEEE Transactions on Power Delivery, Vol. 13, No. 2,
1997, pp. 560-569. doi:10.1109/61.660929
[11] B. A. Mork, “Five-Legged Wound/Core Transformer Model:

A. ABBASI ET AL. 482
Derivation, Parameters, Implementation, and Evaluation,”
IEEE Transactions on Power Delivery, Vol. 14, 1999, pp.
1519-1526. doi:10.1109/61.796249
[12] Z. A. Rezaei, H. Mohseni, P. M. Sanaye, S. Farha ngi and
R. Iravani, “Performance of Various Magnetic Core Mod-
els in Comparison with the Laboratory Test Results of a
Ferroresonance Test on a 33 KV Voltage Transformer”,
IEEE Power Engineering Society General Meeting, Mon-
treal, 16 October 2006.
[13] W. L. A. Neves and H. Dommel, “On Modeling Iron
Core Nonlinearities,” IEEE Transactions on Power Sys-
tems, Vol. 8, No. 2, 1993, pp. 417-425.
doi:10.1109/59.260845
[14] G. Kavasseri, “Analysis of Subharmonic Oscillations in a
Ferroresonant Circuit,” Electrical Power and Energy
Systems, Elsevier Journal, Vol. 28, No. 3, 2005, pp. 207-
214.
[15] Z. Emin, B. A. T. Zahawi, Y. K. Tong and M. Ugur,
“Quantification of the Chaotic Behavior of Ferroresonant
Voltage Transformer Circuits,” IEEE Transactions on
Circuits and Systems, Fundamental Theory and Applica-
tions, Vol. 48, No. 6, June 2001, pp. 757-760.