Energy and Power Engineering, 2011, 3, 450-477
doi:10.4236/epe.2011.34056 Published Online September 2011 (http://www.SciRP.org/journal/epe)
Analytical Approach for the Systematic Research of the
Periodic Ferroresonant Solutions in the Power Networks
Fathi Ben Amar1,2, Rachid Dhifaoui2
1Department of Technology, Preparatory Institute for Engineering Studies of Sfax (IPEIS), Sfax, Tunisia
2Electric Networks and Machines Research Unit, Insat, Tunisia
Received June 7, 2011; revised July 17, 2011; accepted July 24, 2011
Abstract
Ferroresonance is a complex and little known electrotechnical phenomenon. This lack of knowledge means
that it is voluntarily considered responsible for a number of unexplained destructions or malfunctioning of
equipment. The mathematical framework most suited to the general study of this phenomenon is the bifurca-
tion theory, the main tool of which is the continuation method. Nevertheless, the use of a continuation proc-
ess is not devoid of difficulties. In fact, to continue the solutions isolats which are closed curves, it is neces-
sary to know a solution belonging to this isolated curve (isolat) to initialise the continuation method. The
principal contribution of this article is to develop an analytical method allowing systematic calculation of this
initial solution for various periodic ferroresonant modes (fundamental, harmonic and subharmonic) appear-
ing on nonlinear electric system. The approach proposed uses a problem formulation in the frequency do-
main. This method enables to directly determine the solution in steady state without computing of the tran-
sient state. When we apply this method to the single-phase ferroresonant circuits (series and parallels con-
figurations), we could easily calculate an initial solution for each ferroresonant mode that can be established.
Knowing this first solution, we show how to use this analytical approach in a continuation technique to find
the other solutions. The totality of the obtained solutions is represented in a plane where the abscissa is the
amplitude of the supply voltage and the ordinate the amplitude of the system’s state variable (flux or voltage).
The curve thus obtained is called “bifurcation diagram”. We will be able to then obtain a synthetic knowl-
edge of the possible behaviors of the two circuits and particularly the limits of the dangerous zones of the
various periodic ferroresonant modes that may appear. General results related to the series ferroresonance
and parallel ferroresonance, obtained numerically starting from the theoretical and real cases, are illustrated
and discussed.
Keywords: Transformer, Ferroresonance, Fundamental Mode, Harmonic Mode, Subharmonic Mode,
Fractional Mode, Isolat, Limit Point, Bifurcation, Dangerous Zone
1. Introduction
The ferroresonance is a nonlinear resonance phenome-
non that can affect the electrical transmission and distri-
bution networks. It indicates all oscillating phenomena,
generally periodic, which particularly appear on all net-
works at capacitive dominant (single-phase or polyphase)
in interaction with a ferromagnetic nonlinear element
(unloaded transformer).
This phenomenon is characterized by the possibility of
existence of several stable steady states for a given con-
figuration and parameter values. These various operating
modes, except the normal state, are obviously undesir-
able. They lead indeed either to out-of-tolerance over-
voltages with values several times in excess of the net-
work nominal voltage (case of fundamental or harmonic
ferroresonance), or to overcurrents not less dangerous for
the material (case of subharmonic ferroresonance) [1-4].
Modeling a ferroresonant circuit leads to a set of
nonlinear differential Equations depending on various
physical parameters. The mathematical framework ada-
pted to the study of these dynamic systems is the bifurca-
tion theory [4-7]. The essential tool within this frame-
work is the continuation method. It makes it possible to
obtain a global view of the phenomenon and to answer to
concrete problems faced by the power system operator.
However, in order that this continuation method can
function correctly, we must have an initial solution be-

F. B. AMAR ET AL.451
longing to the type of studied mode (fundamental, har-
monic or subharmonic). This difficulty is particularly
obvious in the case of the follow-up of a solutions isolat:
no trivial solution is available to start the continuation.
We thus need a systematic method of determination of
this initial solution for the various ferroresonant modes
[6-8].
In this study, we are interested uniquely in permanent
periodic solutions (fundamental, harmonics and subhar-
monics) in single-phase. Our objective is to develop an
analytical approach which enables us to solve the ini-
tialization problem, on the one hand, in the iterative cal-
culation of the Galerkin method (very effective method
to detect the occurrence conditions of the permanent fer-
roresonance) [4-7] and, on the other hand, in the con-
tinuation techniques used in the bifurcation methods.
At the beginning, we present the studied ferroresonant
system, which corresponds to a series or parallel sin-
gle-phase circuit, in mathematical form. We carry out a
change of variables in order to simplify the study and to
obtain a system of normalized Equations with a reduced
number of unknowns. Then, we present the systematic
stages of calculation of the various types of periodic
modes, solutions of the standardized system. Finally, we
show that this approach can be used in a continuation
technique, which enables to give information on the ex-
istence limits of phenomenon when a parameter varies.
We detail the influence of the supply voltage and the
losses.
Based on real and theoretical circuit cases, we show
the wealth of information to acquire by this analytical
approach. Several results of continuation (bifurcation
diagrams) concerning the fundamental mode, harmonics
3, 5 and 7 modes and subharmonics 3, 5, 7, 9 and 5/3
modes, are presented. That enables us to provide a global
vision of the phenomena and their occurrence zones.
2. Presentation of the Proposed Analytical
Method
As the solutions in steady state are generally periodic,
one seeks a formulation in frequency mode of the prob-
lem. The proposed analytical approach applies the same
principle used in the Galerkin method. The idea is to
seek a periodic solution in the form of Fourier series. For
that, a circuit modeling is adopted, without the nonlinear
element, based on the equivalent Thevenin model (Fig-
ure 1).
The magnetic characteristic i(
 ) of nonlinear induc-
tance, often modelling an unloaded transformer, consti-
tutes the most significant point in the occurrence of fer-
roresonance. It is described by the following univocal
E
th
i(

)
Z
th
v
i
Figure 1. Equivalent study circuit.
relation between the current i and flux
 :


21
;,,
q
iab qab 

 

 (1)
This is an approximate but satisfactory representation
permitting the study of ferroresonance.
For each frequency k, the complex Equation of the cir-
cuit (Figure 1) will be written as follows:
0
kk kk k
jZIE



 (2)
where 
k is the pulsation at frequency k,

k, Ik, Ek, and Zk
are the complex components of the flux, current, supply
voltage and Thevenin equivalent impedance at the har-
monic frequency k.
In simple cases, it is possible to give an analytical ex-
pression to the relations of the current harmonic compo-
nents Ik in function of those of flow

k. Such a procedure
can be appropriate if the harmonic rate of the periodic
modes is limited to the signals having only one or two
spectral components. The Equations are then sufficiently
simple so that one can analytically find a solution. It is
even possible in this case to find all the problem solu-
tions. These simplified solutions can be used to initialize
the Galerkin method and the continuation techniques
used in the bifurcation methods [4-7].
2.1. Equivalent Circuit Equations
Considering  (t) an approximate solution limited at order
2:


1cos() cos;1 h
tt ht  

h

 
(3)
where  is the pulsation at 50 Hz of the excitation. Ex-
cept the fundamental ferroresonance, the row h can be a
multiple of the unit (case of the harmonic ferroresonance)
or a fraction of this one (case of the subharmonic fer-
roresonance).
The Equation (2) is converted into a nonlinear alge-
braic system of 4 Equations, as follows:
0
hch hsh hc
hRIXI



 (4a)
0
hsh hch hs
hRIXI



 (4b)
111 111cs c
RIX IEs



 (4c)
11111 1
s
cs
RIX IEc



 (4d)

F. B. AMAR ET AL. 452
with:
11 11
11 12
cos ;sin;
cos ;sin;
;.
hhsh
c
cs
cs
h
EeEEeE






 
where e1 and e2 are the coefficients of the Thevenin
equivalent voltage. The harmonic components of the
current are calculated from (1); they are expressed in
function of those of flux. The obtained system (4) has
four Equations with four unknown variables (

1,

h,

and
 ). In order to limit this number of unknowns, it is
interesting to normalize this system.
2.2. Normalization of the System
To determine a particular solution of a system periodic
mode (4), it is preferable to transform it as follows: by
adding member to member the Equation (4a) multiplied
by cos
 and the Equation (4b) multiplied by sin  , we
obtain the Equation (5a). By subtracting member to
member the Equation (4a) multiplied by sin
 and the
Equation (4b) multiplied by cos
 , we obtain the Equation
(5b). We proceed in the same way for the Equations (4c)
and (4d) but in multiplying them by cos
 and sin  , we
thus obtain the Equations (5c) and (5d). The Equations
system (4) becomes:

11 21
,,,,,, 0
hh hhh
hRG XG     (5a)



21 11
,,,,,, 0
hh hh
RGX G     (5b)


1131 141
22
12
,,, ,,,
sin
hh
RGX G
Ee e
 






  (5c)


14 113 1
22
12
,,, ,,,
cos
h
RGX G
Ee e
h

 


 (5d)
with:










11 1
1
21 1
1
311 1
11
4111
11
,,,,,, sin
,,, cos
,,,,,, cos
,,, sin
,,,,,, sin
,,, cos
,,,,,, cos
,,, sin
hhch
hs h
hhch
hs h
hch
sh
hch
sh
GI
I
GI
I
GI
I
GI
I







 







 








2
1
tane
e
 
This system (5) can still be written in the following
form:









11
21
21 11
1131141
14 113 1
2
1131141
2
14 113 1
2
,,,
,,, 0
,,,,,, 0
tan
,,, ,,,
,,, ,,,
,,, ,,,
,,, ,,,
hh h
hh
hh hh
hh
hh
hh
hh
hRG
XG
RGXG
RGX G
RGX G
RGX G
RGX G
E
 




 
 
 








 


 



22
12
ee
(6)
In order to reduce the number of unknowns in (6), it is
necessary to carry out the following change of variable:
*
1
h
QavecQ



 (7)
which enables to write the system (6) in a normalized
general form (8):

 




111 21
21 11
113 114 1
14 1131
,,,,,, 0
,,,,,, 0
tan
,,, ,,,
,,, ,,,
h
hh
hQRG QXGQ
h
RGQX GQ
RGQXGQ
RGQX GQ
 
 

  
 










(8)
which is solved easily.
With 123 are functions limited uniquely
to the three unknowns 
1,
 and
4
,, and GG GG
 

. This enables us to
find a solution of the studied mode.
To find all the corresponding approximate solutions to
a given set of parameters of the study circuit or to ap-
proximately determine the existence zones of the various
ferroresonant modes, it is then sufficient to iterate on the
new variable Q.
This developed tool is general and can adapt to any
type of circuit single-phase. Moreover, it constitutes an
excellent means of search for an initial solution to in-
clude in the iterative calculation of the Galerkin method,
particularly in the case of follow-up of solutions isolat.
In order to explain the implementation of this analyti-
cal method, we present it in detail in the following para-
graph.
3. Application to Study of Single-Phase
Ferroresonance
The ferroresonance can occur in single-phase or poly-
phase circuits. The circuit configurations under which

F. B. AMAR ET AL.453
249
this phenomenon can occur are endless [9-11]. We dis-
tinguish the configurations known as series (resp. paral-
lel), where we find a capacity in series (resp. in parallel)
with the nonlinear element and the source voltage.
Frequently, the encountered practical situations are
generally three-phase but, thanks to an adapted modeling,
they can be transformed into single-phase ferroresonance
cases [2-4]. This is why we have chosen in our study a
single-phase representation of the studied system (series
or parallel type).
3.1. Study of Parallel Ferroresonance
We apply the proposed approach to the research of the
periodic ferroresonant modes of the circuit of Figure 2,
which enables to study the problems of the parallel fer-
roresonance. It is about a single-phase model of an op-
eration of voltage restoration between a sinusoidal volt-
age source and an unloaded power transformer, through
an underground cable or a long overhead line [10]. It is
the capacity of the line which is the responsible element
revealing the phenomenon.
The physical parameters of this circuit are:
E: amplitude of the supply voltage e(t) = E cos(100t),
Ct: equivalent capacitance of the circuit,
Lg, Ld: linear inductances of the circuit,
Rg, Rd: series losses of the circuit,
Rt: parallel losses of the circuit.
The magnetic characteristic is defined by:

3
1,841061 10i



   . It corresponds to a real
power transformer, single-phase, of 360 MVA and
nominal primary voltage 130 kV.
By a judicious choice of the circuit parameters, we can
determine the various possible modes of fundamental,
harmonic and subharmonic ferroresonance [12-15].
3.1.1. Search for Integer Subharmonics Modes
In this case, the row h is a simple fraction of the unit. To
fix the ideas, we detail here the example of the subhar-
monic mode 3 (h = 1/3, we use the notation SH3). We
choose the case where the study circuit parameters (Fig-
ure 2) are: Lg = 2.25 H; Rg = 4 ; Ct = 43.5 F; Rt = 0.1
M; Ld = 0.1 H; Rd = 1 , which represent a theoretical
case allowing the study of the SH3.
i= f(

)
e(t)
R
g
L
g
R
d
L
d
R
t
Figure 2. Parallel, single-phase, nonlinear ferroresonant cir-
cuit.
We start then by calculating the Fourier coefficients of
the harmonic currents I1 and I1/3 by virtue of relation i(  ).
We obtain:
11 1223
3
4455
11 12233
3
4455
16 67 78
991010
16 67 78 8
991010
cos coscos
cos cos
sin sinsin
sin sin
coscos cos
cos cos
sinsin sin
sin sin
c
s
c
s
3
8
I
BB B
BB
IB BB
BB
IB B B
BB
IB B B
BB















 





(9)
with:
98 27
1111 1111
333 3
63 45
11 11
33
872 365
9
2111111
33 3
83654
9
3111111
333
2
9
411
126 6302520
256
5040 7560
504 126037805040
256
252 15121260
256
252
256
b
Bk
k
B
k
B
k
B

 
4
11
3


  












 








745
11
33
27
9
511
3
9872
6111 1111
33
36 54
111
3
9276345
9
71 111111
3333
504
36
256
126 6302520
256
5040 7560
84 151216803780
256
h
k
B
b
Bk
k
B



 











 












27 6345 9
8111111
333
836 9
91111
33
36 9
101 1
3
12 3 4
5678
910
756 12602520
256
72 252
256
84
256
;2;4;2
72;;3,23;
6; 36
k
B
k
B
k
B
 
 

5;


 





















 
 

F. B. AMAR ET AL. 454
The system (4) is converted into:

 

111112233
33
44551112
3
334455
cossinsinsin
3
sinsincos cos
cos cos cos0
RB BB
BB XBB
BBB

2






 
 
 (10a)




111112 23
33
44551112
3
334455
sincoscoscos
3
coscossin sin
sinsinsin 0
RB BB
BB XBB
BBB

3
2






 
 
 (10b)



161667788
9910101 6677
8899 10101
cossin sin sin
sinsincos cos
cos coscoss
RB B B
BBXB B
BBB E
 


 

 
 
 (10c)



16166778 8
9910101 6677
8899 10101
sincos cos cos
coscossin sin
sin sinsinc
RB B B
BB XBB
BBB E
 


 

 
 
 (10d)
By adding the Equation (10a) multiplied by cos
th

1 and
e Equation (10b) multiplied by sin

1, we obtain the
Equation (11):
111 1213
3333
14 151213
333 3
14 15
33
sin
3
)sin2 (cos
cos 20
XBRB RB
RBRBX BXB
XB XB





 




 




 







(11)
with  = 3  −  .
the Equation (10a) multiplied by sin

1
fr
By subtracting
om the Equation (10b) multiplied by cos

1, we obtain
the Equation (12):
1112 1314 15
333 33
13 1215 14
33 33
coscos 2
sinsin 20
RBRB RBRB RB
XB XBXB XB



 




 



(12)
We proceed in the same way for the Equations (10c)
and (10d) but by multiplying them by cos

6 and sin

6,
thus we obtain the Equations (13) and (14):

 
 
116 1817
110 191718
22
191101 26
sinX BRBRB  



 
1617 18
19 1101718
22
191101 26
cos
cos 2sin
sin 2cos
RBRB RB
RBRBXBXB
XBXBEee








(14)

Equations (11)-(14) constitute a system of four Equa-
tions in four unknowns 
1,

1/3,
 and  . To reduc
number of unknowns to three, we adopt the follo
change of variable:
e the
wing
1
3
1
QQR



 (15)
We show that, forQ a given value of , we can com-
pletely solve the Equations system (11) to (14) and to
deduce an approximate solution from
tem (2). The supply voltage amplitu
termined by the ratio between the two Equations (13) and
(1
the complete sys-
de E is directly de-
4). By varying Q, we thus compute all the solutions of
the characteristic for SH3 mode in function of the source
voltage E. By using the terminology of the bifurcation
theory, the curve thus obtained in the plane, where the
abscissa is the amplitude E and the ordinate is the ampli-
tude of the system’s state variable (flux or voltage), is
called “bifurcation diagram”. Then we will be able to
then get information on the existence zone of the mode
studied in function of the voltage E and to precise its
critical values which correspond to limit point bifurca-
tions [4-6].
By replacing the functions Bi (i =1 à 10) by their expres-
sions and

1/3 per Q·

1 in the two Equations (11) and (12)
where there is not source component, we obtain:
8
9
111 11114
33 33
1512 13
sin
3 256
sin2coscos 20
kXXP
RPX PXP

 







33 3
kRP






 
 

(16)


8
9
1111 1112
333 3
1314 15
333
cos
256
cos 2sinsin20
k
kRR PR P
RPXPX P
 
 









 



sin 2cos
cos 2sin
RBRBX BXB
XBXBEee


(17)
where the elements Pi (i = 1 a 5) are polynomials in Q:
A first solution of the Equations (16) and (17) is 
1/3 =
8642
1
753
2
64
4
64
5
126 25207560 5040 63
75652926300 1260
25222683780 1260
216 504
PQQQQ
PQQQ Q
Q
PQQQQ
PQQ
  
  
  

3
753
288 504PQ
0


 
 
(13)
 

F. B. AMAR ET AL. 455
0: it corresponds to the harmonic modes. To calculate the
subharmonic modes, let us eliminate component
-2
-1
0
3
8
9
1
256
k

between the Equations (16) and (17). We obtain a rela-
tion in

of type:
ecossincos2sin2abc d
  
  (18)
with:
12
33
22
14 114114
33
3
bX P XkPkRP
3
13
3
22
15 115115
33 3
11
3
3
3
3
cRP
dXPXkPkR P
eR P
aRP






 

In order to solve relation (18), we make the following
change of variables:
(19)
which enables to write the relation (18) in form of a sys-
tem of two nonlinear Equations to two unknowns (x and
y):
(20)
In order to determine whether the system admi
y) = 0 is the Equation of unit circle.
For a fixed value of Q and under condition x2 + y2 = 1
(condition which fixes the interval of Q for whic
mode exists), the tracing of the representative curves of
th



22
sin telque1 avec ,1,1
cos
xxy xy
y



 



2
22
,22 0fxycx bxaydxyce




,1 0gxyxy


ts solu-
tions on [–1, 1], we will plot the representative curves of
the two functions f and g in order to show the existence
of a couple (x, y) where they intersect. Let us note that
g(x,
h a SH3
e two functions f and g of the system (20) shows the
existence of two intersection points S1(x1, y1) et S2(x2, y2)
(Figure 3).
Knowing  , the Equation (17) enables to calculate 
1.
Then

1/3 is given by the relation (15):
11
3
Q


Parameter α is deduced by the ratio between the two
1
2
-3 -2 -1 01 23
x = sin

y
= cos

f,y)=0(x
S
1
g
(x,y)=0
S
2
Figure 3. Intersection of the two representative curves of the
functions f(x, y) = 0 and g(x, y) = 0.
Equations (13) and (14): (see Equation (21))
Knowing
 , the same Equations (13) and (14) also
enable to calculate the amplitude of source voltage E.
Finally, the parameter
 is deduced starting from the
relation (13):

1
3

 
In this way, we can easily solve the initialization prob-
lem observed in the continuation procedures used in the
bifurcation method, and in the iterative calculation pro-
cedure used in the Galerkin method. The latter method
enables to calculate precisely the ferroresonant modes.
We present, in Figure 4, the solution waveforms ob-
tained by the proposed approach (flux  (t) in the target
transformer and the voltage V(t) on its terminals), over a
period, for the peak value of the nominal voltage (E =
183 kV): it is about a solution of SH3 mode. Indeed, its
basic period is three times as equal as the excitation pe-
riod T0 = 20 ms. It is then easy to note that, under the
influence of the presence of the 1/3 harmonic component,
the solution waveform is obviously deformed.
From this solution, we vary progressively the parame-
ter Q, the two intersection points and system (20) solu-
tions. Then, we generate two SH3 solution branches
which meet in two limit points BP1 and BP2 (Figure
5(a)), called bifurcation points for which there is stability
change. Thus, we obtain a bifurcation diagram of the
SH3 ferroresonant mode (noted DB-SH3). To have an
overall view of the results, we present this bifurcation
diagram in function of voltage E for each variable (
 , V,

1, V1,

1/3, V1/3): they are solution isolats (Figures 5(a)
and (b)).
On the other hand, the diagram surface (in other words




 


 
116 181711019171819110
1617 1819 110
ncosRBRB RBRB RB17 1819110
sinsin2cos cos2
cos 2sinsin2
X BRBRBRBRBXBXBX BX B
X BX BX BX B
 
ta 

 
   (21)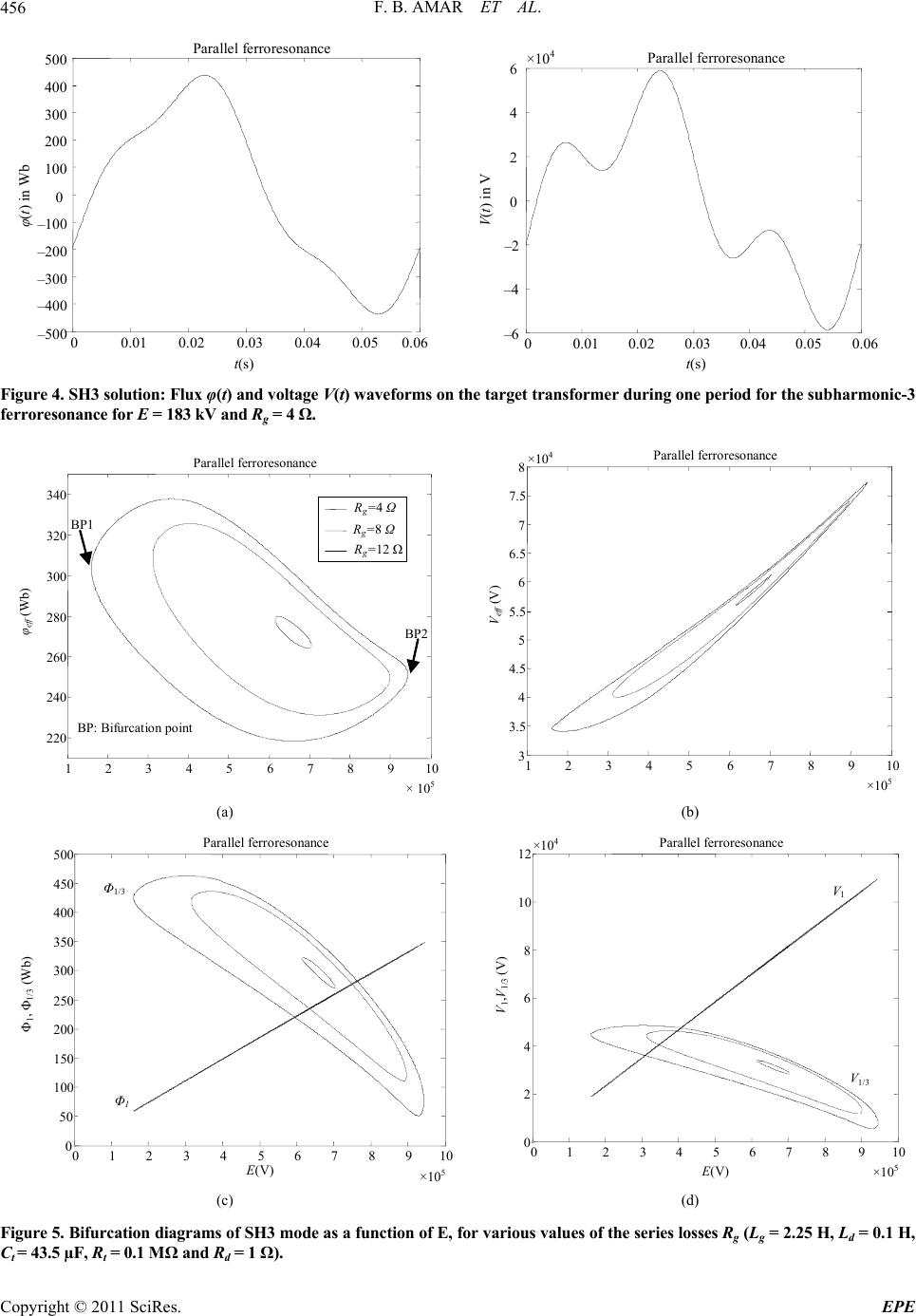
  

F. B. AMAR ET AL. 456
0 0.01 0.02 0.03 0.04 0.050.06
–
500
–
400
–
300
–
200
–
100
0
100
200
300
400
500
t
(
s
)
φ(t) in Wb
Parallel ferroresonance
00.01 0.02 0.03 0.04 0.05 0.06
–6
6×10
4
Parallel ferroresonance
–
4
–2
0
2
4
V
(t) in V
t(s)
e target transformer during one period for the subharmonic-3 Figure 4. SH3 solution: Flux φ(t) and voltage V(t
ferroresonance for E = 183 kV and R = 4 Ω.
) waveforms on th
g
1 2 3 4 56 7 8 910
× 10
5
220
240
260
280
300
320
340
Parallel ferroresonance
φ
e
ff
(Wb)
R
g
=4 Ω
R
g
=8 Ω
R
g
=12 Ω
BP1
BP2
BP: Bifurcation point
12345 6 7 8 910
×10
5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8×10
4
Parallel ferroresonance
(V)
ff
V
e
(a) (b)
0 1 2 3 45 6 7 89 10
×10
5
0
50
100
150
200
250
300
350
400
450
500
E
(V)
Φ
1
, Φ
1/3
(Wb)
Parallel ferroresonance
Φ
1
Φ
1/3
01 2 3 45 6 7 89 1
0
×10
5
0
2
4
6
8
10
12 ×10
4
E
(V)
V
1
,V
1/3
(V)
Parallel ferroresonance
V
1/3
V
1
(c) (d)
Figure 5. Bifurcation diagrams of SH3 mode as a function of E, for various values of the series losses Rg (Lg = 2.25 H, Ld = 0.1 H,
Ct = 43.5 µF, Rt = 0.1 MΩ and Rd = 1 Ω).

F. B. AMAR ET AL. 457
the existence zone of mode SH3) is more reduced when
series losses Rg of system are large. In addition, the
minimum voltage of the existence of this ferroresonant
mode (where the first bifurcation BP1) increases. In con-
trast, the maximum voltage of existence (where the sec-
ond bifurcation BP2) decreases. Indeed, in order that this
mode persists, it is necessary that the source energy can
compensate for the network losses [16,17]. This remains
possible for strong voltages. But these voltages are not
realistic for an electrical power network. The considera-
tions above also apply to the other types of periodic fer-
roresonant modes.
Let us announce that, for certain values of E, the am-
plitude of SH3 component can exceed considerably the
amplitude of the 50 Hz component (Figure 5(b)). In fact,
the ratio Q (15), which enab
pared to that 50 Hz, has for valu
The same reasoning is equally applied to calculate the
other subharmonics modes. On Figures 6-11, we sum-
marize the results of the proposed approach concerning
modes SH5, SH7 and SH9 (these are theoretical cases).
Qualitatively, the remarks previously quoted on the
DB-SH3 are retained for the DB-SH5, DB-SH7 and
DB-SH9.
On Figure 12, we compare the bifurcation diagrams of
the subharmonics 3, 5, 7, 9 modes and the fundamental
mode, which can exist simultaneously for the following
theoretical case: Lg = 2.25 H, Rg = 1 , Ct = 1100 F, Rt
= 0.1 M and Ld = Rd = 0. We then conclude that:
 Contrary to the fundamental ferroresonance mode,
the bifurcation diagrams of the subharmonics modes
are solution isolats and no intersection with trivial
solutions.
 The existence domains o
e flux  (t) and the
voltage V(t) decrease when the row of subharmonic
increases. These values are always lower than those
reached by the fundamental ferroresonance mode.
 For the same excitation voltage E, different subhar-
monic solutions can exist. One or the other of the so-
lutions appears according to the value of the initial
conditions (initial charge on capacitor, remanent flux
in the core of the target transformer, switching instant,
etc.).
This methodology permits to treat effectively the ini-
tialization problems encountered in the Galerkin method
and the continuation methods.
3.1.2. Search for Fractional Subharmonics Modes
1982, EDF recorded a ferroresonance case during th
lectric generators of Chas-
tang on transformers of nuclear power stations of Chinon
[5]. Abnormal oscillations at a preponderant frequency
of 83.33 Hz are observed. This frequency corresponds to
a period
les to relativize the SH3 com-
e several times the unit. voltage feedback from hydroe
In e
0
3
5
T (with T0 = 20 ms is the source period).
We apply the proposed analytical method to simulate
this mode type, solution of the circuit of Figure 2 mod-
eling the voltage feedback.
We consider two flux components 
1 and

5/3 (h = 5/3
is not a simple unit fraction) and we adopt the following
values: Lg = 2.25 H, Rg = 20 , Ct = 4.5 F, Rt = 0.1 M,
Ld = 0.1 H and Rd = 7 , which correspond to a line of
nominal voltage 225 kV of 370 km and give a network
natural frequency of
150 Hz
2π
r
f
gt
LC

 (22)
The Galerkin Equations system of is:
f these oscillation modes
decrease when the row of subharmonic increases.
The effective values reaching by th
0 0.01 0.02 0.03 0.040.05 0.06 0.070.080.09 0.1
-500
-400
-300
-200
-100
0
100
200
300
400
500
Parallel ferroresonance
00.01 0.020.03 0.040.050.06 0.07 0.08 0.090.1
-4
-3
t
(
s
)
φ(t) in Wb
-2
-1
0
1
2
3
4×10
4
Parallel ferroresonance
V n V(t) i
t(s)
Figure 6. SH5 solution: Flux φ(t) and voltage V(t) waveforms
ferroresonance for E = 183 kV.
on the target transformer during one period for the subharmonic-5

F. B. AMAR ET AL. 458
0 0.5 1 1.5 2 2.53
240
250
260
270
280
290
300
310
320
330
340 Parallel ferroresonance
00.511.5 2 2.53
E
(V)
φ
e
ff
(Wb)
BP1
BP2
BP: Bifurcation point
×10
6
×106
2
3
4
5
6
7
8×104Parallel ferroresonance
Ve
ff
(V)
E
(V)
(a)
0 0.5 1 1.5 2 2.5 3
×106
0
50
100
150
200
250
300
350
400
450
500 Parallel ferroresonance
E
(V)
Φ1, Φ1/5 (Wb)
Φ1
Φ1/5
00.5 11.52 2.5 3
×10
6
0
2
4
6
8
10
12×10
4
Parallel ferroresonance
V
1
V
1
, V
1/5
(V)
E
(
V
)
V
1/5
(b)
Figure 7. Bifurcation diagrams of SH5 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H,
Rt = 0.1 MΩ, Rg = 1 Ω and Rd = 0.5 Ω. (a) Existence zones of the SH5 mode versus applied voltage E. (b) Continuation
plitudes of SH5 component and the 50 Hz component.
Ct = 129 µF,
of the am-
0 0.020.040.060.08 0.10.120.14
-500
-400
-300
-200
-100
0
100
200
300
400
500 Parallel ferroresonance
φ(t) in Wb
t(s)
00.020.040.060.08 0.1 0.120.14
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
×10
4
Parallel ferroresonance
V
(
t
)
in V
t
(
s
)
Figure 8. SH7 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the subharmonic-7
ferroresonance for E = 183 kV.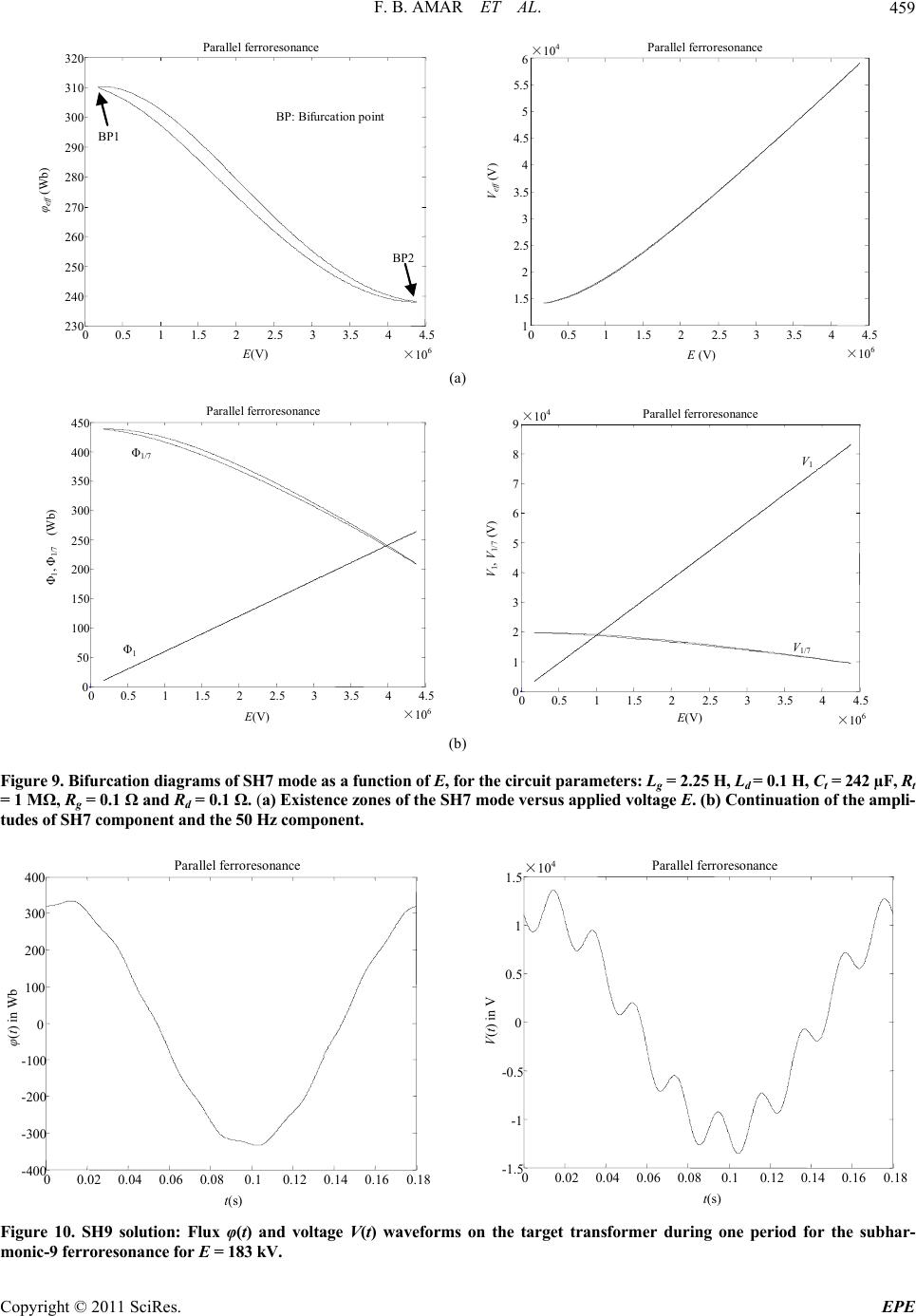

F. B. AMAR ET AL.459
0 0.5 1 1.5 22.5 3 3.5 44.5
×10
6
230
240
250
260
270
280
290
300
310
320
Parallel ferroresonance
φ
e
ff
(Wb)
E
(V)
BP: Bifurcation
p
oint
BP1
BP2
00.511.5 22.5 3 3.5 44.5
×106
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6×104Parallel ferroresonance
Ve
ff
(V)
E
(V)
(a)
0 0.51 1.52 2.5 3 3.544.5
×10
6
0
50
100
150
200
250
300
350
400
450
Parallel ferroresonance
Φ
1
, Φ
1/7
(Wb)
E
(V)
Φ
1
Φ
1/7
00.5 11.5 22.5 3 3.5 4 4.5
×10
6
0
1
2
3
4
5
6
7
8
9×10
4
Parallel ferroresonance
E
(V)
V
1
, V
1/7
(V)
V
1/7
V
1
(b)
Figure 9. Bifurcation diagrams of SH7 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 242 µF, Rt
= 1 MΩ, Rg = 0.1 Ω and Rd = 0.1 Ω. (a) Existence zones of the SH7 mode versus applied voltage E. (b) Continuation of the ampli-
tudes of SH7 component and the 50 Hz component.
00.02 0.04 0.060.080.1 0.120.140.160.18
-1.5
-1
-0.5
0
0.5
1
1.5×10
4
Parallel ferroresonance
V(t) in V
t(s)
0 0.02 0.04 0.06 0.08 0.10.120.140.160.18
-400
-300
-200
-100
0
100
200
300
400
Parallel ferroresonance
φ(t) in Wb
t(s)
Figure 10. SH9 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the subhar-
monic-9 ferroresonance for E = 183 kV.

F. B. AMAR ET AL. 460
0 0.5 1 1.5 22.5 3 3.544.5
×10
6
180
190
200
210
220
230
240
Parallel ferroresonance
φ
e
ff
(Wb)
E
(V)
BP: Bifurcation point
BP1
BP2
Parallel ferroresonance
00.5 11.5 2 2.5 3 3.5 44.5
×10
4×
10
4
3.5
6
0.5
1
1.5
2
2.5
3
(V)
ff
e
V
(V)
E
(a)
0 0.5 1 1.5 22.53 3.544.5
×10
6
0
50
100
150
200
250
300
350
Parallel ferroresonance
E
(V)
Φ
1
, Φ
1/9
(Wb)
Φ
1
Φ
1
/9
00.511.52 2.53 3.5 44.5
×10
6
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5×
10
4
Parallel ferroresonance
V
1
,V
1/9
(V)
E
(V)
V
1
V
1/9
(b)
Figure 11. Bifurcation diagrams of SH9 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 370
µF, Rt = 100 MΩ, Rg = 1 mΩ and Rd = 0 Ω. (a) Existence zones of the SH9 mode versus applied voltage E. (b) Continuation of
the amplitudes of SH9 component and the 50 Hz component.
01 2345 67
×10
7
0
100
200
300
400
500
600
700
800
900
Parallel ferroresonance
D
B-fondamental
D
B-SH7
D
B-SH5
D
B-SH3
D
B-SH
9
φ
eff
(Wb)
E(V)
0 1 2 3 4 5 6 7
×10
7
0
0.5
1
1.5
2
2.5
3
×10
5
Parallel ferroresonance
D
B-
f
ondamental
D
B-SH3
D
B-S
H
5
D
B-SH7
D
B-SH9
V
eff
(V)
E (V)
Figure 12. Comparison between bifurcation diagrams of SH3, 5, 7, 9 modes and of fundamental mode for the circuit parame-
ters: Lg = 2.25 H, Ld = 0 H, Ct = 1100 µF, Rt = 0.1 MΩ, Rg = 1 Ω and Rd = 0 Ω.

F. B. AMAR ET AL. 461
555 55
333 33
555 55
333 33
111111
111 11 1
50
3
50
3
cs c
scs
cs c
sc sc
RIX I
RIX I
RIX IE
RIX IE




 
 
 
 
s
(23)
We obtain a subharmonic 3 mode (Figure 13) whose
harmonic 5 of frequency 0
583.33 Hz
3
ff (with
0
0
150 HzfT
 is the source frequency) is preponderant
in its spectrum. It is the synchronization phenomen
between the natural period of the free system
on
0
3
5
T
T
without excitation or losses (called Hamiltonian system)
and the source period T0, which gives us a fractional
subharmonic mode SH3/5 oscillating at a common pe-
riod which is here 3T0. We announce that for the ordi-
nary ferroresonant circuits, the maximum period of free
oscillation is about 100 ms at a few seconds and the
minimal period is about of the millisecond.
The continuation of this mode in function of the exci-
tation E is summarized by the bifurcation diagrams of
Figure 14: it is an isolat, result awaited for the subhar-
monics modes. These diagrams show that, for the net-
work parameters values, ferroresonance may occur for
nominal phase-to-neutral network voltage 130 kV (wh
ther the possible initial condition values are responsib
for initiating ferroresonance).
alculation of the periodic modes, of the same excitation
period, rich in harmonic h. In this case, flux is described
by two harmonic components 
1 and

h with h positive
integer. We speak about the harmonic h mode (we use
the notation Hh) when the amplitude 
h becomes impor-
tant and superior to 
1.
We study, in this paragraph, the harmonic 3, 5 and 7
modes, for real situations of Figure 2. Setting of Equa-
tions is similar to that adopted for the subharmonics
modes.
Figure 15 shows, for Enom = 183 kV, the waveforms of
flux  (t) and voltage V(t) at the transformer terminals in
search case for a H3 mode. By examining these curves,
we note that each one contains three similar maximums
ource period; that means that the solution -
ed is very rich in harmonic 3 (f = 150 Hz). The con-
tinuation of this mode, in function of the excitation volt-
age E begins with the null trivial solution (  = 0, V = 0)
for E = 0 (Figure 16). When E increases, one meets two
bifurcations of the limit point type BP1 and BP2 specify-
ing the true zone of existence of the H3 mode. In fact,
inside this zone where the tension E is understood be-
tween 152 kV and 240 kV, the amplitude of the
third-harmonic component (V3) is important in front of
the fundamental component 50 Hz (V1) (Figure 16(b))
and the corresponding solutions are characterized by
dangerous overvoltages (the nominal amplitude of the
network voltage is 183 kV).
On Figures 17-20, we summarize the results of the H5
and H7 modes (they are real cases). Qualitatively, the
arks previously quoted on the DB-H3 are retainedor
-H5 and DB-H7.
To have an overall view of the results, we compare the
real case: Lg = 2.25 H, Rg = 20 , Ct = 1 F, Rt = 0.1 M,
Ld = 0.1 H and Rd = 7 . Then we conclude that:
over a sob
tain
e-
le
rem f
the DB
3.1.3. Search for Harmonics Modes
e apply the method previously described for systematic
bifurcation diagrams of the harmonic 3, 5, 7 modes and
the fundamental mode (Figures 21) for the following
W
c
0 0.01 0.02 0.03 0.04 0.05 0.06
-800
-600
-400
-200
0
200
400
600
800
Parallel ferroresonance
φ
(
t
)
in Wb
t
(s)
00.010.020.03 0.04 0.05 0.06
-3
-2
-1
0
1
2
3×10
5
Parallel ferroresonance
V(t) in V
t(s)
Figure 13. SH3/5 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the frac-
tional subharmonic-3/5 ferroresonance for E = 183 kV.

F. B. AMAR ET AL. 462
Parallel ferroresonance
0.6 0.8 1 1.2 1.4 1.6 1.82
×10
5
345
350
355
360
365
370
375
E
(V)
φ
e
ff
(Wb)
BP: Bifurcation
BP1
BP2
0.6 0.811.2 1.4 1.6 1.82
×10
5
1.15
1.2
1.25
1.3
1.35
1.4
1.45
Parallel ferroresonance
×10
5
V
e
ff
(V)
E
(
V
)
(a)
0.6 0.8 1 1.21.4 1.6 1.82
×10
5
0
100
200
300
400
500
600 Parallel ferroresonance
0.6 0.8 11.2 1.4 1.6 1.82
×10
5
0.2
0.4
Φ
1
, Φ
3/5
(Wb)
E
(V)
Φ
3/5
Φ
1
0.6
0.8
1
1.2
1.4
1.6
1.8
Parallel ferroresonance
V
1
, V
3/5
(V)
V
1
×10
5
E
(
V
)
V
3/5
(b)
Figure 14. Bifurcation diagrams of SH3/5 mode as a function of E
. (a) Existence zones of t
, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 4.5
he SH3/5 mode versus applied voltage E. (b) Continuation of µF, Rt = 0.1 MΩ, Rg = 20 Ω and Rd = 7 Ω
the amplitudes of SH3/5 component and the 50 Hz component.
0 0.002 0.0040.006 0.008 0.01 0.012 0.0140.0160.0180.02
-600
-400
-200
0
200
400
600
Parallel ferroresonance
00.0020.0040.0060.0080.01 0.012 0.014 0.0160.0180.02
-4
-3
-2
-1
0
1
2
3
4×10
5
Parallel ferroresonance
t
(
s
)
φ
(
t
)
in Wb
t(s)
V(t) in V
Figure 15. H3 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the harmonic-3
ferroresonance for E = 183 kV.

F. B. AMAR ET AL.463
Parallel ferroresonance
0 0.5 1 1.52 2.5 3
×10
5
0
50
100
150
200
250
300
350
400
450
500
E
(V)
BP : Bifurcation
BP2
BP1
φ
e
ff
(Wb)
00.5 11.52 2.53
×10
5
0
0.5
1
1.5
2
2.5
3
3.5
Parallel ferroresonance
E
(V)
V
e
ff
(V)
(a)
0 0.5 1 1.5 2 2.53
×10
5
0
100
200
300
400
500
600
700
Parallel ferroresonance
E
(V)
Φ
1
, Φ
3
(Wb)
Φ
3
Φ
1
00.5 11.5 2 2.5 3
×10
5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Parallel ferroresonance
E
(V)
V
1
, V
3
(V)
V
1
V
3
×10
5
(b)
Figure 16. Bifurcation diagrams of H3 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 1 µF,
Rt = 0.1 MΩ, Rg = 20 Ω and Rd = 7 Ω. (a) Existence zones of the H3 mode versus applied voltage E. (b) Continuation of the
amplitudes of H3 component and the 50 Hz component.
0 0.002 0.0040.006 0.008 0.01 0.0120.0140.0160.0180.02
-600
-400
-200
0
200
400
600
Parallel ferroresonance
φ(t) in Wb
t(s)
00.002 0.004 0.006 0.008 0.01 0.012 0.0140.0160.018 0.02
-4
-3
-2
-1
0
1
2
3
4×10
5
Parallel ferroresonance
t (s)
V
(t) in
V
Figure 17. H5 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the harmonic-5
ferroresonance for E = 183 kV.

F. B. AMAR ET AL. 464
0 0.51 1.5 2 2.5 3
0
50
100
150
200
250
300
350
400
450 Parallel ferroresonance
BP : Bifurcation point
E
(V)
φ
e
ff
(Wb)
BP1
BP2
×10
5
00.5 11.5 2 2.5 3
0
0.5
1
1.5
2
2.5
3
3.5 Parallel ferroresonance
E
(V)
V
e
ff
(V)
×10
5
×10
5
(a)
0 0.5 1 1.5 2 2.5 3
0
100
200
300
400
500
600 Parallel ferroresonance
E
(V)
Φ
1
, Φ
5
(Wb)
Φ
1
Φ
5
×10
5
00.511.5 2 2.5 3
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Parallel ferroresonance
E
(V)
V
1
, V
5
(V)
V
5
V
1
×10
5
×10
5
(b)
Figure 18. Bifurcation diagrams of H5 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 0.333
µF, Rt = 0.1 MΩ, Rg = 20 Ω and Rd = 7 Ω. (a) Existence zones of the H5 mode versus applied voltage E. (b) Continuation of the
amplitudes of H5 component and the 50 Hz component.
0 0.0020.004 0.006 0.008 0.01 0.012 0.014 0.0160.0180.02
-600
-400
-200
0
200
400
600
Parallel ferroresonance
t
(s)
φ(t) in Wb
00.0020.0040.0060.0080.01 0.0120.0140.0160.0180.0
2
-4
-3
-2
-1
0
1
2
3
4
Parallel ferroresonance
t
(
s
)
V
(t) in V
×10
5
Figure 19. H7 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer uring one period for the harmonic-7
ferroresonance for E = 183 kV.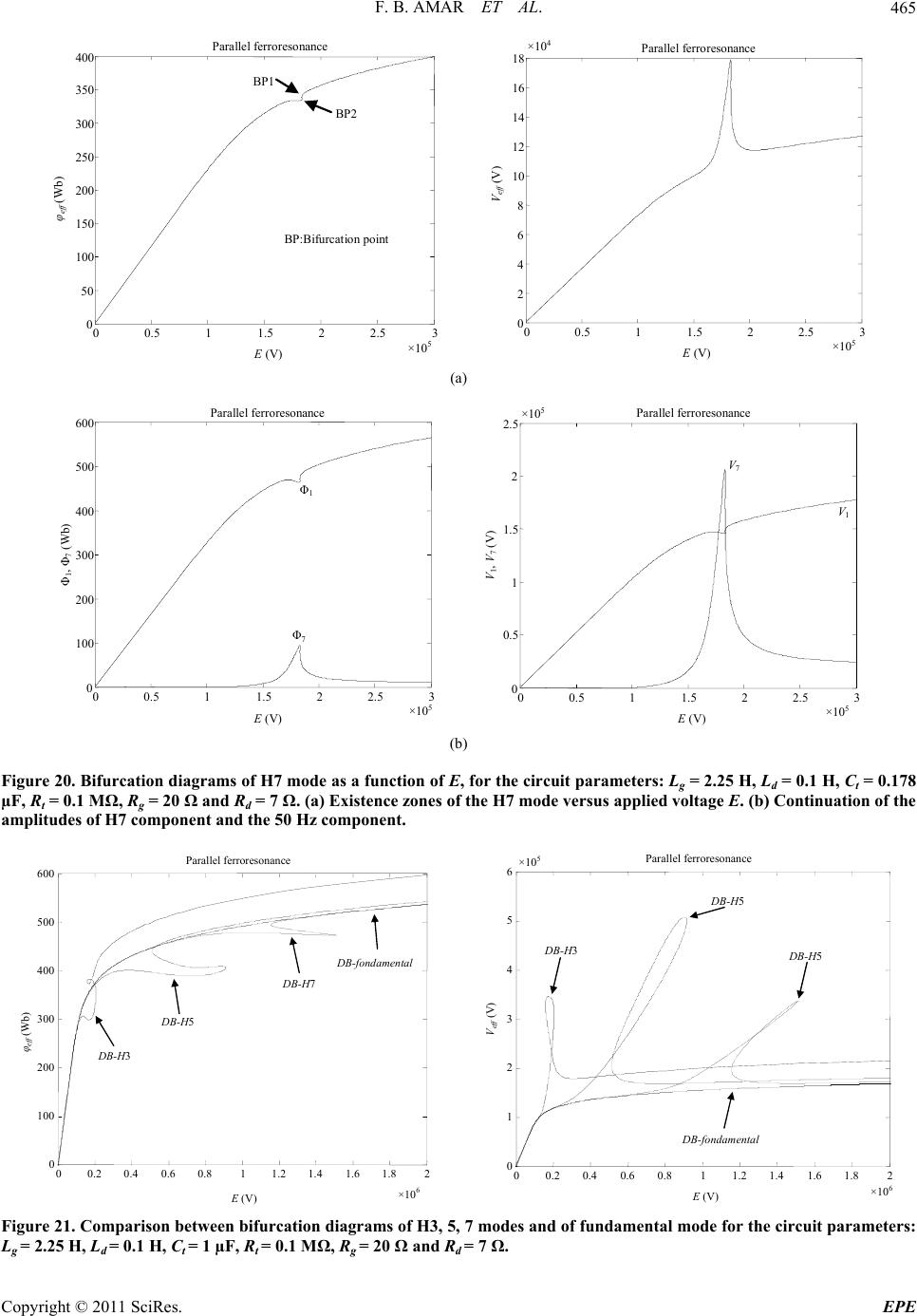

F. B. AMAR ET AL.465
0 0.5 1 1.5 2 2.5 3
0
50
100
150
200
250
300
350
400 Parallel ferroresonance
E
(V)
φ
eff
(Wb)
BP:Bifurcation point
BP1
BP2
×10
5
00.5 11.5 2 2.5 3
0
2
4
6
8
10
12
14
16
18 Parallel ferroresonance
V
e
ff
(V)
E
(V) ×10
5
×10
4
(a)
0 0.5 1 1.52 2.5 3
0
100
200
300
400
500
600 Parallel ferroresonance
E
(V)
Φ1, Φ7 (Wb)
Φ1
Φ7
×105
00.5 11.5 2 2.5 3
0
0.5
1
1.5
2
2.5 Parallel ferroresonance
E
(V)
V1, V7 (V)
V7
V1
×105
×105
(b)
Figure 20. Bifurcation diagrams of H7 mode as a function of E, for the circuit parameters: Lg = 2.25 H, Ld = 0.1 H, Ct = 0.178
µF, Rt = 0.1 MΩ, Rg = 20 Ω and Rd = 7 Ω. (a) Existence zones of the H7 mode versus applied voltage E. (b) Continuation of the
amplitudes of H7 component and the 50 Hz component.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
100
200
300
400
500
600
Parallel ferroresonance
D
B-H3
D
B-H5
D
B-H7
D
B-fondamental
E
(V)
φ
e
ff
(Wb)
×10
6
00.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
1
2
3
4
5
6
Parallel ferroresonance
D
B-H3
D
B-H5
D
B-H5
D
B-fondamental
E
(V)
V
e
ff
(V)
×10
5
×10
6
Figure 21. Comparison between bifurcation diagrams of H3, 5, 7 modes and of fundamental mode for the circuit parameters:
Lg = 2.25 H, Ld = 0.1 H, Ct = 1 µF,
Rt = 0.1 MΩ, Rg = 20 Ω and Rd = 7 Ω.

F. B. AMAR ET AL. 466
 The bifurcation diagrams of the harmonic modes are
complex curves always starting with the null trivial
solution.
 The existence domains of these oscillation modes and
their voltage levels E increase when the row h of har-
monic increases. The existence minimum voltages are
much become large as the row h is large. For h > 3,
they are clearly higher than the nominal voltage.
 The voltage domain E situated between the existence
superior limit of H3 mode and the existence inferior
limit of the H5 mode is probably rich of the
four-harmonic component (it is the H4 mode).
 The source voltage applied is then determining final
mode: in fact, while varying in a monotonous way the
excitation voltage E, we observe in the increasing or-
der the appearance of the various harmonic modes
(even and odd).
 The maximum rms values reached by the voltage V(t)
(overvoltages) are always superior to those reached
by the fundamental mode.
3.2. Study of Series Ferroresonance
We apply this method to computation of the periodic
ferroresonant modes of the circuit of Figure 22, which
describes correctly the practical problems of the series
ferroresonance. Most commonly, this type of situation is
achieved when a magnetic voltage transformer (the
nonlinear inductance) is connected to busbar separated
by the grading capacitance of an open circuit breaker (th
series capacitance) [1-4]. This capacitance is the capital
element revealing the ferroresonance.
by
ll capacitances of the circuit breaker, the transformer
and the busbar section,
l: linear inductance of the circuit,
R1 and R2: series and parallel losses of the circuit.
The magnetic characteristic is defined by:
49
e
The physical parameters of this circuit are:
E: amplitude of the supply voltage e(t) = E cos(100t),
C: equivalent capacitance of the circuit, constituted
a
33
( )102,34.10i




voltage transformer, single
. It corresponds to a real
-phase, of nominal primary
i=f(

)
e(t)
C
R
1
l
R
2
s
Figure 22. Series, single-phase, nonlinear ferroresonant cir-
uit.
only two solutions. Obtaining one or another depends on
the in
voltage 230 kV.
We adopt the values R1 = 32 k; C = 400 pF; R2 = 714
M and l = 0 H, which represents a real case allowing
the simultaneous study of the various possible ferroreso-
nant modes (fundamental, subharmonics 3, 5, 7, 9 and
3/5 and harmonics 3, 5 and 7).
3.2.1. Search for Integer Subharmonics Modes
The row h is a simple fraction of the unit. Figures 23-26
respectively give the initial solutions of the SH3, SH5,
SH7 and SH9 modes, obtained for the crest value of the
nominal voltage Enom = 327 kV.
From these initial solutions, we vary step-by-step the
ntinuation parameter Q; we obtain the correspding
bifurcation diagrams: they are solution isolats compris-
ing two bifurcation points as in the case of the parallel
ferroresonance (Figures 27-30).
Likewise the existence zones of these subharmonics
modes are reduced as the parallel losses of the system
become large. Indeed, the phenomenon disappears as
soon as the losses become important. All this confirms
the regulate action that parallel losses have on the vari-
ous phenomena of the series ferroresonance; their role is
much more important than the series losses.
The superposition of the obtained bifurcation dia-
grams and that of the fundamental mode is given by
Figure 31. We find the same conclusions as that of the
parallel ferroresonance. The levels of flux  (t) and volt-
age V(t), for the same circuit parameter decrease when
e row of subharmonic increases and they areways
lower than those reached by the fundamental ferroreso-
We apply the method to the situation where h is not a
simple unit fraction, by studying the case of the frac-
tional subharmonic mode SH3/5. We obtain a subhar-
monic 3 mode (Figure 32) whose harmonic 5 (83.33 Hz:
which represents the frequency of the phenomenon stud-
ied SH3/5) is predominating only for unrealistic values
of E (Figure 33(b)).
By examining the oscillation waveform of the ob-
tained solution (Figure 32), for E = Enom = 327 kV, we
observe that it contains three maximums over a period;
that means that this solution is rich in harmonic 3 (50
Hz).
The continuation of this mode as a function of E gives
a bifurcation diagram (solutions isolat) comprising 4
singularities BP1, BP2, BP3 and BP4 (Figure 33(a)). We
note that for certain excitation voltage values E, four
olutions are possible, whereas for others, the system has
itial conditions.
co on
th al
nance mode.
3.2.2. Search for Fractional Subharmonics Modes
c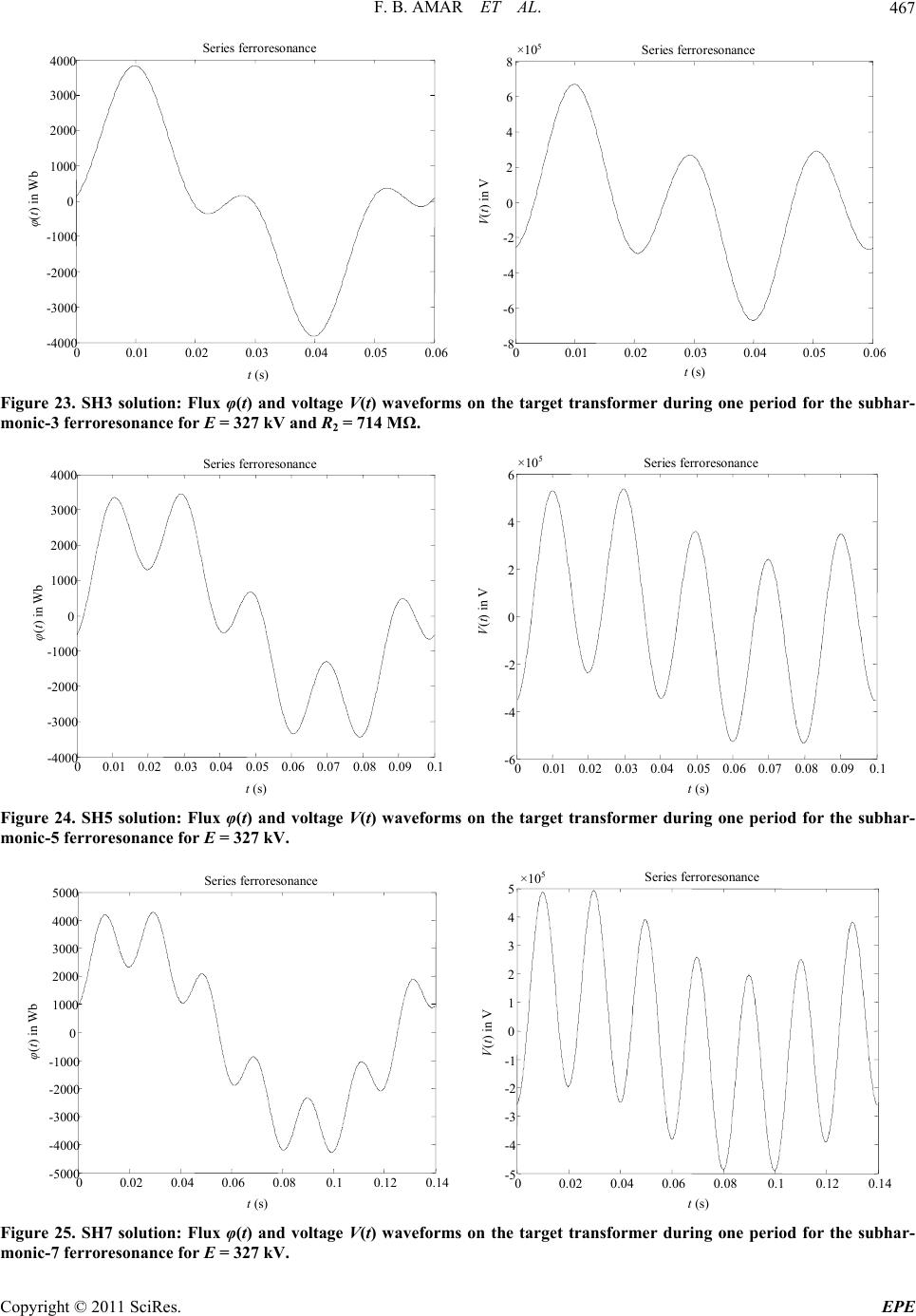

F. B. AMAR ET AL. 467
0 0.01 0.02 0.03 0.04 0.050.0
6
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000
Series ferroresonance
t
(
s
)
φ(t) in Wb
00.01 0.02 0.03 0.04 0.05 0.06
-8
-6
-4
-2
0
2
4
6
8
Series ferroresonance
n V
s o
ce for E = 327 kV and R = 714 MΩ.
V(t) i
t (s)
n the target transformer during one period for the subhar-
×10
5
Figure 23. SH3 solution: Flux φ(t) and voltage V(t) waveform
monic-3 ferroresonan2
0 0.010.02 0.030.040.05 0.060.07 0.080.090.1
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000 Series ferroresonance
t
(s)
φ(t) in Wb
00.01 0.020.03 0.040.05 0.06 0.07 0.080.090.1
-6
-4
-2
0
2
4
6
Series ferroresonance
V
×105
V(t) in
t (s)
Fi s o gure 24. SH5 solution: Flux φ(t) and voltage V(t) waveform
monic-5 ferroresonance for E = 327 kV.
n the target transformer during one period for the subhar-
0 0.02 0.040.06 0.08 0.10.120.14
-5000
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000
5000
Series ferroresonance
φ(t) in
t (s)
Wb
00.02 0.04 0.06 0.08 0.1 0.120.1
4
-5
-4
-3
-2
-1
0
1
2
3
4
5
Series ferroresonance
×10
5
V(t) in V
t (s)
n the target transformer during one period for the subhar-Figure 25. SH7 solution: Flux φ(t) and voltage V(t) waveform
monic-7 fe
s o
rroresonance for E = 327 kV.

F. B. AMAR ET AL. 468
0 0.02 0.04 0.06 0.08 0.1 0.12 0.140.160.1
8
-5000
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000
5000
Series ferroresonance
φ(t) in Wb
t (s)
00.020.040.060.080.10.12 0.14 0.160.18
-5
-4
-3
-2
-1
0
1
2
3
4
5
Series ferroresonance
V
(t) in V
t (s)
×105
Figure 26. SH9 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the subhar-
monic-9 ferroresonance for E = 327 kV.
0 1 2 3 45 6 7 89 10
1500
2000
2500
3000
3500
Series ferroresonance
E
(V)
φ
e
ff
(Wb)
BP: Bifurcation point
BP1
BP2
R
2
=32 MΩ
R
2
=50 MΩ
R
2
=714 MΩ
×10
5
0 12 3 45 6 7 8 910
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
Series ferroresonance
E
(V)
V
e
ff
(V)
×10
5
×10
5
(a)
0 1 2 3 45 6 7 89 1
0
0
500
1000
1500
2000
2500
3000
3500
4000
4500
Series
ferroresonance
0 1 2 3 45 6 7 8 9 1
0
E(V)
0
1
2
3
4
5
6
7
8
9
10
Series ferroresonance
V
1
, V
1/3
(V)
V
1/3
V
1
×10
5
×10
5
Φ
1/3
Φ
1
E
(V)
Φ
1
, Φ
1/3
(Wb)
×10
5
(b)
Figure 27. Bifurcation diagrams of SH3 mode as a function oor various values of the parallel losses R2 (Ct = 400 pF, = f E, fR1
32 kΩ and l = 0 H). (a) Existence zones of the SH3 mode versus applied voltage E. (b) Continuation of the amplitudes of SH3
component and the 50 Hz component.

F. B. AMAR ET AL. 469
0 1 2 3 4 5 6 7 8
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
Series ferroresonance
E
(V)
V
e
ff
(V)
×10
5
×10
5
0 1 2 34 5 6 7 8
1500
1600
1700
1800
1900
2000
2100
2200
2300
2400
2500 Series ferroresonance
E
(V)
φ
eff
(Wb)
BP1
BP2
BP: Bifurcation point
×10
5
(a)
0 1 2 34 5 6 78
0
500
1000
1500
2000
2500
3000
3500 Series ferroresonance
0 1 2 34 5 6 7 8
0
1
2
3
4
5
6
7
8
Series ferroresonance
E
(V)
Φ1, Φ1/5 (Wb)
Φ1/5
Φ1
×105
1
, V
1/5
(V)
V
E
(V)
V
1
V
1/5
×10
5
(b)
Figure 28. Bifurcation diagrams of SH5 mode as a function , for the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct =
400 pF and l = 0 H. (a) Existence zones of the SH5 mode versus applied voltage E. (b) Continuation of the amplitudes of SH5
component and the 50 Hz component.
3.2.3. Search for Harmonics Modes
We apply the method to the study of the harmonic modes
3, 5 and 7. Figures 34-36 give, over a period, the wave-
forms of their corresponding solutions. By examining
these waves, we note that they respectively contain 3, 5
and 7 maximums over a period; that means that the three
solutions obtained are respectively very rich in harmonic
3 (f = 150 Hz), in harmonic 5 (f = 250 Hz) and in har-
monic 7 (f = 350 Hz). These three solutions are theoreti-
cal and do not represent any realistic situations for an
electrical power network (E Enom = 327 kV).
The continuation of these modes, as a function of the
excitation voltage E, begins with the null trivial solution
for E = 0 and presents four bifurcation points BP1, BP2,
d by the two singu-
larities BP1 and BP2. However the studied harmonic
modes are in a voltage interval which does not interest
the power system operator (the nominal phase-to-neutral
network voltage 230 kV). Their existence zones are de-
limited by the two singularities BP3 and BP4.
We compare the bifurcation diagrams of the harmonic
3, 5, 7 modes and of the fundamental mode (Figure 40),
we find the same conclusions of the parallel ferroreso-
nance. The bifurcation diagrams always start with the
null trivial solution. The levels of flux  (t) and voltage
V(t), for the same circuit parameter, are always superior
those reached by fundamental ferroresonant mode.
e source voltage applied is determining final mode.
Indeed, while varying in a monotonous way the excita-
odd).
×10
5
of E

to
Th
BP3 and BP4 (Figures 37-39). For realistic voltage val-
ues, the mode can be normal or fundamental ferroreso-
nance: the existence zone is delimite
tion voltage E, we observe in the increasing order the
appearance of the various harmonic modes (even and

F. B. AMAR ET AL. 470
In all the treated examples, the ferroresonance phenom-
ena appear only in the lightly loaded electrical networks..
In addition, it is necessary that these circuits are under
the good initial conditions so that these phenomena are
generated.
4. Conclusions
Ferrorresonance is a very complex nonlinear phenome-
non which affects power transmission system and distri-
bution system. It is a particular case of bifurcation of
nonlinear dynamic system. We are thus interested in the
initialization question of the continuations of several
modes types.
We have presented in this study an analytical method
for research from the periodic ferroresonant solutions.
This approach enables us to systematically calculate the
periodic modes intervening in the single-phase ferrore-
sonance. The association of this method with a continua-
tion technique enables to obtain the limits of the exis-
tence domains of the dangerous and undesirable modes
as a function of source voltage E. We have presented, on
real and theoretical configurations, parallel and series,
the wealth of the informations brought by this analytical
approach. Indeed, several results of continuation con-
cerning the fundamental mode, harmonics 1, 3, 5 and 7
modes and subharmonics 3, 5, 7, 9 and 3/5 modes are
presented. It comes from this study the following overall
conclusions:
 The risks of ferroresonant phenomena in the electrical
power networks have an important appearance prob-
ability.
0 1 2 34 5 6 7 8
2100
2200
2300
2400
2500
2600
2700
2800
2900
Series ferroresonance
φ
e
ff
(Wb)
E
(V)
BP1
BP2
BP: Bifurcation point
×10
5
0 1 2 34 5 6 7 8
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5 Series ferroresonance
V
e
ff
(V)
E
(V)×10
5
×10
5
(a)
0 1 2 34 5 6 78
0
500
1000
1500
2000
2500
3000
3500
4000
4500
Series ferroresonance
Φ
1
, Φ
1/7
(Wb)
E
(V) ×10
5
Φ
1/7
Φ
1
0123 4 5 6 7 8
0
1
2
3
4
5
6
7
Series ferroresonance
8
V
1
V
1/7
(V) ,
E
(V)
V
1/7
×10
5
for the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct = 4
plied voltage E. (b) Continuation of the amplitudes of SH7
×10
5
V
1
(b)
E,
s ap
Figure 29. Bifurcation diagrams of SH7 mode as a function of
nF and l = 0 H. (a) Existence zones of the SH7 mode versu
component and the 50 Hz component.

F. B. AMAR ET AL.471
0 0.5 1 1.5 2 2.53 3.5
4
2300
2350
2400
2450
2500
2550
2600
2650
2700
Series ferroresonance
BP: Bifurcation point
BP1
φ
eff
(Wb)
BP2
E
(V) ×10
5
00.5 11.5 22.5 3 3.5 4
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
Series ferroresonance
V
e
ff
(V)
×10
5
E
(V) ×10
5
) (a
0 0.5 1 1.52 2.5 33.5
4
0
500
1000
1500
2000
2500
3000
3500
4000 Series ferroresonance
E
(V)
Φ
1
, Φ
1/5
(Wb)
Φ
1/5
Φ
1
×10
5
0.5 11.5 22.5 3 3.5
4
0.5
1
1.5
2
2.5
3
3.5
4Series ferroresonance
E
(V)
V
1
, V
1/5
(V)
V
1
V
1/5
×10
5
×10
5
(b)
Figure 30. Bifurcation diagrams of SH9 mode as a function or the circuit parameters: R2 = 7140 MΩ, R1 = 32 kΩ, Ct = 4
nf and l = 0 H. (a) Existence zones of the SH9 mode versus d voltage E. (b) Continuation of the amplitudes of SH9
component and the 50 Hz component.
f E,
applie
fo
0 24 68 10 121
4
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
Series ferroresonance
φe
ff
(Wb)
E
(V)
D
B-fondamental
D
B-SH3
D
B-SH5
D
B-SH7
D
B-SH9
×105
02468 10 12 14
0
2
4
6
8
10
12
14
16
Series ferroresonance
V
e
ff
(V)
E
(
V
)
D
B-
f
ondamenta
l
D
B-SH3
D
B-SH5
D
B-SH7
D
B-SH9
×10
5
×10
5
Figure 31. Comparison between bifurcation diagrams of SH3, 5, 7, 9 modes and of fundamental mode for the circuit parame-
ters: R2 = 714 MΩ, R1 = 32 kΩ, C = 400 pF and l = 0 H.

F. B. AMAR ET AL. 472
0 0.01 0.02 0.030.04 0.050.06
-6000
-4000
-2000
0
2000
4000
6000 Series ferroresonance
φ (t) in Wb
t (s)
00.01 0.020.03 0.04 0.050.0
6
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Series ferroresonance
V
(t) in V
t (s)
×10
6
Figure 32. SH3/5 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the frac-
tional subharmonic-3/5 ferroresonance for E = 327 kV.
0 0.2 0.4 0.60.81 1.2 1.41.6 1.8
2
2950
3000
3050
3100
3150
3200
3250
Series ferroresonance
BP: Bifurcation point
BP1
BP2
BP3
BP4
φ
eff
(Wb)
E
(V) ×10
5
00.20.40.60.81 1.21.4 1.61.82
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
Series ferroresonance
V
e
ff
(V)
E
(V) ×10
6
×10
6
(a)
0 0.20.4 0.60.81 1.21.4 1.61.82
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000 Series ferroresonance
E
(V)
Φ
1
, Φ
3/5
(Wb)
Φ
3/5
Φ
1
×10
6
00.2 0.40.6 0.8 1 1.21.4 1.61.8
2
0
2
4
6
8
10
12
14
16
18
Series ferroresonance
V
1
, V
3/5
(V)
E
(V)
V
1
V
3/5
×10
5
×10
6
(b)
Figure 33. Bifurcation diagrams of SH3/5 mode as a function of E, for the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct =
400 pF and l = 0 H. (a) Existence zones of the SH3/5 mode versus applied voltage E. (b) Continuation of the amplitudes of
SH3/5 component and the 50 Hz component.

F. B. AMAR ET AL.473
Series ferroresonance
Series ferroresonance
0 0.002 0.004 0.0060.0080.010.0120.0140.0160.0180.02
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
5
00.002 0.0040.0060.0080.01 0.012 0.0140.016 0.018 0
φ
(
t
)
in Wb
t (s)
.02
-5
-4
-3
-2
-1
0
1
2
3
4
(t) in V
V
t
(
s
)
Figure 34. H3 solution: Flux φ(t) and voltage V(t) wavefo
×10
6
rms on the target transformer during one period for the harmonic-3
rroresonance for E = 10 MV. fe
Series ferroresonance
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.0
2
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
6
00.0020.0040.0060.0080.01 0.012 0.014 0.016 0.0180.0
φ
(
t
)
in Wb
t
(
s
)
2
-6
-4
-2
0
2
4
Series ferroresonance
V(t) in V
t
(
s
)
×10
6
Figure 35. H5 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the harmonic-5
ferroresonance for E = 20 MV.
Series ferroresonance
00.0020.0040.0060.0080.010.0120.0140.016 0.0180.0
2
-6
-4
-2
0
2
4
6
Series ferroresonance
V(t) in V
×10
6
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.0160.018 0.0
8000
6000
4000
2000
2
-8000
-6000
-4000
-2000
0
)
in Wb
t
(
φ
t
(
s
)
t
(
s
)
Figure 36. H7 solution: Flux φ(t) and voltage V(t) waveforms on the target transformer during one period for the harmonic-7
ferroresonance for E = 30 MV.

F. B. AMAR ET AL. 474
0 0.5 1 1.5 22.
5
0
1000
2000
3000
4000
5000
6000
Series ferroresonance
φ
e
ff
(Wb)
E
(V)
BP: Bifurcation point
BP1
BP2 BP3
BP4
×10
7
00.5 11.52 2.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Series ferroresonance
E
(V)
Ve
ff
(V)
×107
×106
(a)
0 0.5 11.522.5
0
1000
2000
3000
4000
5000
6000
7000
8000
Series ferroresonance
Φ
1
, Φ
3
(Wb)
E
(V)
Φ
3
Φ
1
×10
7
00.5 11.5 2 2.
5
0
1
2
3
4
5
6Series ferroresonance
V
1
, V
3
(V)
E
(V)
V
3
V
1
×10
7
×10
6
(b)
Figure 37. Bifurcation diagrams of H3 mode as a function of E, for the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct = 400
pF and l = 0 H. (a) Existence zones of the H3 mode versus applied voltage E. (b) Continuation of the amplitudes of H3 com-
ponent and the 50 Hz component.
0 0.5 1 1.5 22.5 3 3.5 44.5 5
0
1000
2000
3000
4000
5000
6000
Series ferroresonance
φ
eff
(Wb)
00.5 11.5 22.5 3 3.54 4.55
0
1
2
3
4
5
6Series ferroresonance
V
e
ff
(V)
E (V)
BP: Bifurcation point
BP1
BP2
BP3
BP4
×10
7
×10
6
×10
6
(a)
E
(V) ×10
7

F. B. AMAR ET AL.475
0 0.5 1 1.5 2 2.5 3 3.5 44.5
5
×10
7
0
1000
2000
3000
4000
5000
6000
7000
8000
Series ferroresonance
Φ
1
, Φ
5
(Wb)
E
(V)
Φ
1
Φ
5
00.5 11.522.53 3.5 4 4.55
×10
7
0
1
2
3
4
5
6
7
8
Series ferroresonance
V
1
, V
5
(V)
E
(
V
)
V
5
V
1
×10
6
(b)
Figure 38. Bifurcation diagrams of H5 mode as a function of E, for the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct = 400
pF and l = 0 H. (a) Existence zones of the H5 mode versus applied voltage E. (b) Continuation of the amplitudes of H5 com-
ponent and the 50 Hz component.
0 0.5 1 1.5 22.5 3 3.5 44.5 5
0
1000
2000
3000
4000
5000
6000 Series ferroresonance
BP: Bifurcation point
E
(V)
φ
eff
(Wb)
BP1
BP2
BP3
BP4
×10
7
00.5 11.5 22.5 3 3.5 4 4.55
0
0.5
1
1.5
2
2.5
3
3.5
4
Series ferroresonance
V
e
ff
(V)
E
(V)
×10
6
×10
7
(a)
00.511.5 22.5 3 3.5 4 4.5
5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Series ferroresonance
E
(V)
V
1
, V
7
(V)
V
7
V
1
×10
0 0.5 1 1.5 22.5 3 3.5 44.5 5
0
1000
2000
3000
4000
5000
6000
7000
8000
Series ferroresonance
6
(V)
Φ
1
Φ
1
, Φ
7
(Wb)
Φ
×10
7
7
E
(b)
Figure 39. Bifurcation diagrams of H7 mode as a function of E the circuit parameters: R2 = 714 MΩ, R1 = 32 kΩ, Ct = 400
pF and l = 0 H. (a) Existence zones of the H7 mode versus applied voltage E. (b) Continuation of the amplitudes of H7 m-
ponent and the 50 Hz component.
, for
co

F. B. AMAR ET AL. 476
0 0.5 11.5 22.53 3.544.5 5
0
1000
2000
3000
4000
5000
6000
Series ferroresonance
D
B-fondamental
D
B-H7
D
B-H5
D
B-H3
φ
e
ff
(Wb)
E
(V) ×10
7
00.5 11.522.5 3 3.5 44.55
0
1
2
3
4
5
6Series ferroresonance
D
B-fondamental
D
B-H3
D
B-H5
D
B-H7
E
(V)
V
e
ff
(V)
×10
7
×10
6
Figure 40. Comparison between bifurcation diagrams of H3, 5, 7 modes and of fundamental mode for the circuit parameters:
R2 = 714 MΩ, R1 = 32 kΩ, Ct = 400 pF and l = 0 H.
 For all the series ferroresonances, the phenomenon
can give rise to ferroresonance modes generally peri-
odic of fundamental or subharmonic type. On the
contrary, for all the parallel ferroresonances, the
modes are harmonic type, i.e. fundamental with
strong harmonic amplitudes in the spectrum, but also
pseudoperiodics.
On the practical plane, the approach proposed is a tool
enabling to determine if, in existing and future installa-
tion, there is danger of ferroresonance. It enables to pre-
dict and appraise the ferroresonance possibilities in an
electrical network for the set of the source voltage values
E in normal and downgraded conditions.
The analytical approach developed with two compo-
nents of flux gives us a first estimate of the solution and
constitutes, in general, an excellent starting point for the
iterations of the Galerkin method: a method which offers
solutions closer to reality, owing to the fact that it does
not impose any restriction on the component count of
flux. A study in this direction is presently being pursued.
5. References
[1] K. Pattanapakdee and C. Banmongkol, “Failure of Riser
Pole Arrester Due to Station Service Transformer,” In-
ternational Conference on Power Systems Transients, Lyon,
4-7 June 2007.
[2] S. Santoso, R. C. Dugan and H. Peter, “Modeling Fer-
roresonance Phenomena in an Underground Distribution
System,” International Conference on Power Systems
Transients (IPST’07) Lyon, 4-7 June 2007.
[3] R. C. Dugan, “Examples of Ferroresonance in Distribu-
tion Systems,” IEEE Power Engineering Society General
[5] C. Kieny, “Application of the Bifurcation Theory in
Studying and Understanding the Global Behaviour of a
Ferroresonant Electric Power Circuit,” IEEE Transac-
tions on Power Delivery, Vol. 6, No. 2, 1991, pp. 866-
872. doi:10.1109/61.131146
[6] F. B. Amar and R. Dhifaoui, “Bifurcation Diagrams and
Lines of Period-1 Ferroresonance,” WSEAS Transactions
on Power Systems, Vol. 1, No. 7, 2006, pp. 1154-1162.
[7] F. B. Amar and R. Dhifaoui, “Study of the Periodic Fer-
roresonance in the Electrical Power Networks by Bifur-
cation Diagrams,” International Journal of Electrical
Power and Energy Systems, Vol. 33, No. 1, 2011, pp.
61-85. doi:10.1016/j.ijepes.2010.08.003
[8] B. S. A. Kumar and S. Ertem, “Capacitor Voltage Trans-
former Induced Ferroresonance: Causes, Effects and De-
sign Considerations,” Electric Power Systems Research,
Vol. 21, 1991, pp. 23-31.
[9] S. K. Chakravarthy and C. V. Nayar, “Series Ferroreso-
nance in Power Systems,” International Journal of Elec-
trical Power & Energy Systems, Vol. 17, No. 4, 1995, pp.
267-274. doi:10.1016/0142-0615(95)00045-R
[10] M. Rioual and C. Sicre, “Energization of a No-Load
Transformer for Power Restoration Purposes: Impact of
the Sensitivity to Parameters,” International Conference
on Power Systems Transients (IPST’01), Seattle, Vol. 2,
16 July 2001, pp. 892-895.
[11] N. Janssens, V. Vanderstockt, H. Denoel and P. A. Mon-
fils, “Elimination of Temporary Overvoltages Due to
Ferroresonance of Voltage Transformers: Design and
Testing of Damping System,” International Council on
Large Electric Systems, Paris, 1990, pp. 33-204.
[12] R. G. Kavasseri, “Analysis of Subharmonic Oscillations
in a Ferroresonant Circuit,” International Jonal of
Electrical Power and Energy Systems, Vol. 28No. 3,
2005, pp. 207-214. doi:10.1016/j.ijepes.2005.11.010
ur
,
Meeting, Knoxville, 13-17 July 2003.
[4] Ph. Ferracci, “Ferroresonance,” Cahier Technique, Group
Schneider, 1998.
[13] K. S. Preetham, R. Saravanaselvan and R. Ramanujam,
“Investigation of Subharmonic Ferroresonant Oscillations
in Power Systems,” Electric Power Systems Research,

F. B. AMAR ET AL.477
Vol. 76, No. 9-10, 2006, pp. 873-879.
doi:10.1016/j.epsr.2005.11.005
[14] R. G. Kavasseri, “Analysis of Subharmonic Oscillations
in a Ferroresonant Circuit,” International Journal of
Electrical Power and Energy Systems, Vol. 28, No. 3,
2005, pp. 207-214. doi:10.1016/j.ijepes.2005.11.010
[15] M. V. Escudero, I. Dudurych and M. A. Redfern, “Char-
acterization of Ferroresonant Modes in HV Substation
with CB Grading Capacitors,” Electric Power Systems
Research, Vol. 77, No. 11, 2007, pp. 1506-1513.
doi:10.1016/j.epsr.2006.08.033
[16] S. Mitrea and A. Adascalitei, “On the Prediction of Fer-
roresonance in Distribution Networks,” Electric Power
Systems Research, Vol. 23, No. 2, 1992, pp. 155-160.
doi:10.1016/0378-7796(92)90063-7
[17] M. M. Saied, H. M. Abdallah and A. S. Abdallah,
“Damping Effect of Load on the Ferroresonance Phe-
nomenon in Power Networks,” Electric Power Systems
Research, Vol. 7, 1984, pp. 271-277.
doi:10.1016/0378-7796(84)90011-7