Energy and Power En gi neering, 2011, 3, 422-435
doi:10.4236/epe.2011.34053 Published Online September 2011 (http://www.SciRP.org/journal/epe)
A Novel Fuzzy—Adaptive Hysteresis Controller Based
Three Phase Four Wire -Four Leg Shunt Active Filter for
Harmonic and Reactive Power Compensation
Rathika Ponpandi1, Devaraj Durairaj2
1Electronics and Communication Engineering, Cape Institute of Technology, Levengipuram,
Tamilnadu, India
2Research and Development, Kalasalingam University, Krishnankoil, Tamilnadu, India
Received August 4, 2011; revised September 5, 2011; accepted September 19, 2011
Abstract
This paper presents a fuzzy logic based three phase four wire four-leg shunt active power filter to suppress
harmonic currents. Modified instantaneous p-q theory is adopted for calculating the compensating current.
Fuzzy-adaptive hysteresis band technique is applied for the current control to derive the switching signals for
the voltage source inverter. A fuzzy logic controller is developed to control the voltage of the DC capacitor.
Computer simulations are carried out on a sample power system to demonstrate the suitability of the pro-
posed control strategy, for harmonic reduction under three different conditions namely, ideal, unbalance,
unbalance and distorted source voltage conditions. The proposed control strategy is found to be effective to
reduce the harmonics and compensate reactive power and neutral current and balance load currents under
ideal and non-ideal source voltage conditions.
Keywords: Harmonics, Shunt Active Power Filter (APF), Harmonics, Hysteresis Band, Fuzzy Logic Control,
P-Q Theory
1. Introduction
Active filters are widely employed in distribution system
to reduce the harmonics [1]. Various topologies of active
filters have been proposed for harmonic mitigation. The
shunt active power filter based on Voltage Source In-
verter (VSI) structure is an attractive solution to har-
monic current problems. The shunt active filter is a Pulse
Width Modulated (PWM) voltage source inverter that is
connected in parallel with the load. Active filter injects
harmonic current into the AC system with the same am-
plitude but with opposite phase as that of the load. The
principal components of the APF are the Voltage Source
Inverter (VSI), DC energy storage device, coupling in-
ductance and the associated control circuits. The per-
formance of an active filter depends mainly on the tech-
nique used to compute the reference current and the con-
trol strategy followed to inject the compensation current
into the line.
There are two major approaches that have been pro-
posed in the literature for harmonic detection, namely,
frequency domain and time domain methods [2]. The
time domain methods require less computation and are
widely followed for computing the reference current.
The two mostly used time domain methods are synchro-
nous reference (d-q-0) theory [3] and instantaneous
real-reactive power (p-q) theory [4,5]. Though p-q theory
has good transient response time and steady state accu-
racy [6], it is found to be not suitable for estimating ref-
erence current under non-ideal source voltage conditions.
Hence modified Instantaneous p-q theory [7,8] is fol-
lowed in this work for harmonic detection.
There are several control strategies proposed in the lit-
erature for current control namely, PI control [2], predic-
tive current control [9], Sliding Mode Control (SMC) [10]
and hysteresis control [11]. Among the various current
control techniques, hysteresis control is the most com-
monly used method because of its simplicity in imple-
mentation. But, with fixed hysteresis band, the slope of
the reference current is unpredictable [12], which leads
to increase in switching frequency. Dell Aquila [13] have
proposed a hysteresis current controller with fixed
switching frequency which results in low current track-
ing error [14]. But this method gives high value of THD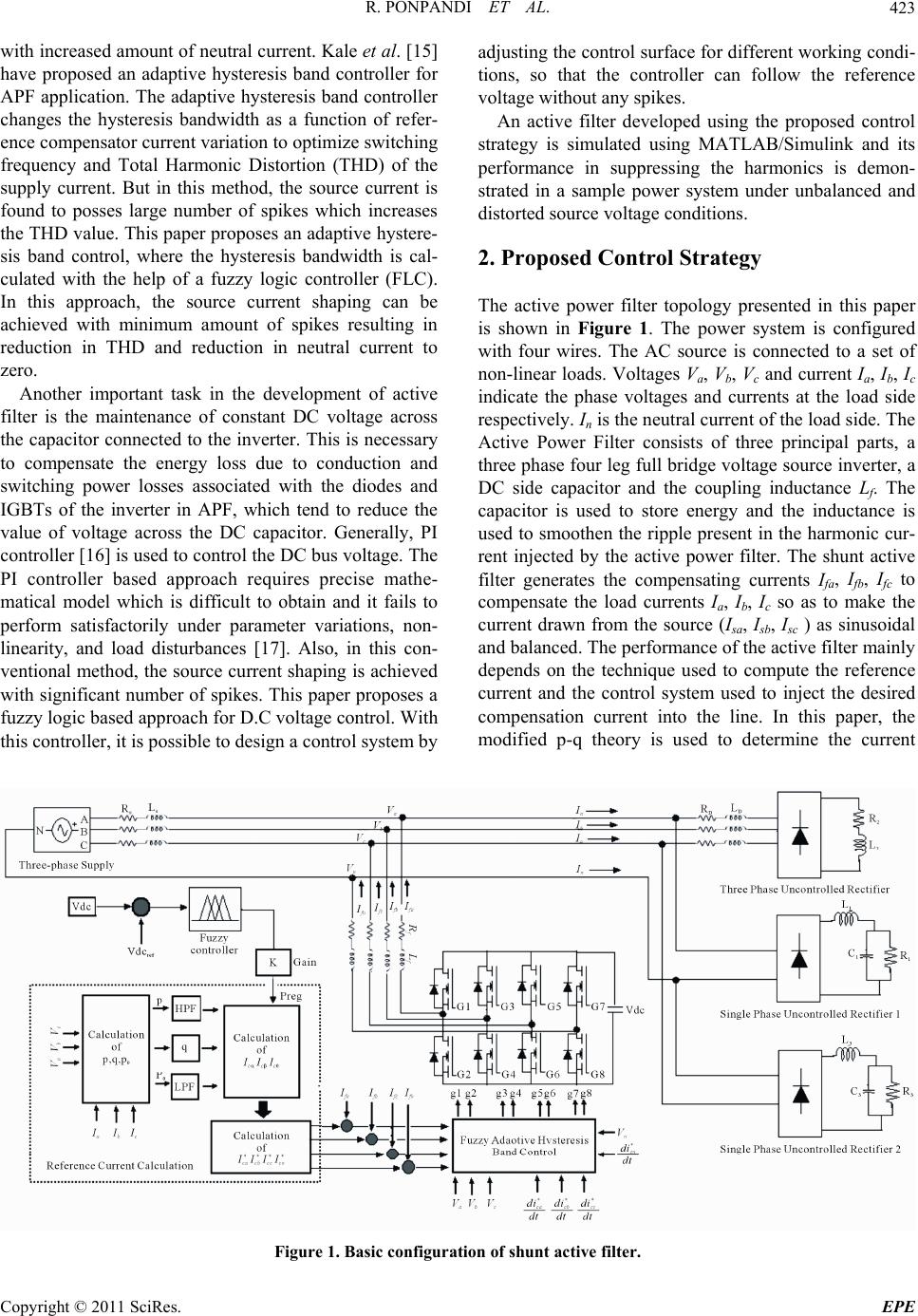

R. PONPANDI ET AL.423
with increased amount of neutral current. Kale et al. [15]
have proposed an adaptive hysteresis band controller for
APF application. The adaptive hysteresis band controller
changes the hysteresis bandwidth as a function of refer-
ence compensator current variation to optimize switching
frequency and Total Harmonic Distortion (THD) of the
supply current. But in this method, the source current is
found to posses large number of spikes which increases
the THD value. This paper proposes an adaptive hystere-
sis band control, where the hysteresis bandwidth is cal-
culated with the help of a fuzzy logic controller (FLC).
In this approach, the source current shaping can be
achieved with minimum amount of spikes resulting in
reduction in THD and reduction in neutral current to
zero.
Another important task in the development of active
filter is the maintenance of constant DC voltage across
the capacitor connected to the inverter. This is necessary
to compensate the energy loss due to conduction and
switching power losses associated with the diodes and
IGBTs of the inverter in APF, which tend to reduce the
value of voltage across the DC capacitor. Generally, PI
controller [16] is used to control the DC bus voltage. The
PI controller based approach requires precise mathe-
matical model which is difficult to obtain and it fails to
perform satisfactorily under parameter variations, non-
linearity, and load disturbances [17]. Also, in this con-
ventional method, the source current shaping is achieved
with significant number of spikes. This paper proposes a
fuzzy logic based approach for D.C voltage control. With
this controller, it is possible to design a control system by
adjusting the control surface for different working condi-
tions, so that the controller can follow the reference
voltage without any spikes.
An active filter developed using the proposed control
strategy is simulated using MATLAB/Simulink and its
performance in suppressing the harmonics is demon-
strated in a sample power system under unbalanced and
distorted source voltage conditions.
2. Proposed Control Strategy
The active power filter topology presented in this paper
is shown in Figure 1. The power system is configured
with four wires. The AC source is connected to a set of
non-linear loads. Voltages Va, Vb, Vc and current Ia, Ib, Ic
indicate the phase voltages and currents at the load side
respectively. In is the neutral current of the load side. The
Active Power Filter consists of three principal parts, a
three phase four leg full bridge voltage source inverter, a
DC side capacitor and the coupling inductance Lf. The
capacitor is used to store energy and the inductance is
used to smoothen the ripple present in the harmonic cur-
rent injected by the active power filter. The shunt active
filter generates the compensating currents Ifa, Ifb, Ifc to
compensate the load currents Ia, Ib, Ic so as to make the
current drawn from the source (Isa, Isb, Isc ) as sinusoidal
and balanced. The performance of the active filter mainly
depends on the technique used to compute the reference
current and the control system used to inject the desired
compensation current into the line. In this paper, the
modified p-q theory is used to determine the current
Figure 1. Basic configuration of shunt active filter.

R. PONPANDI ET AL. 424
references (Ica*, Icb*, Icc*). In Figure 1, the blocks indi-
cated inside the dotted line corresponds to the reference
er. The source ref-
current calculation. A fuzzy logic controller with error
(between the capacitor voltage and reference voltage)
and change in error as input and real power requirement
as output is developed to control Vdc.
A fuzzy adaptive HBCC is used for generating the re-
quired switching signals for the invert
erence current
*
d
d
f
a
i
t and the supply voltage


s
vt are
given as input and te hysteresis bandwidth is tutput hhe o
of the fuzzy controller. The details of reference current
ference Current
Onportant tasks involved in the devel-
opment of an active filter is the formulation of harmonic
-wire system are first transformed into a
th
computation, fuzzy-logic based D.C voltage control and
fuzzy adaptive hysteresis band control are presented in
the subsequent sections.
3. Algorithm for Re
Calculation
e of the most im
detection method. In this work, the modified instantane-
ous active and reactive power theory (p-q theory) [6] is
employed to calculate instantaneously the reference cur-
rents. The modified p-q algorithm is a combination of
p-q algorithm and a positive sequence voltage detector
algorithm.
In this method the voltages and currents from the three
phase four
ree-axis representation α-β-0, using the following
equations:
0
V


 12 1212
211
212
3
03232
a
b
c
V
VV
VV








 

 


 
(1)
012 1212
211212
3
03232
a
b
c
I
I
I
I
I
I



 

 


 

 


 





(2)
The power components p and q are related to the α-β
voltages and currents, and can be written together as
given below,
I
VV
p
VV
I
q
 
 


 
 



 (3)
The instantaneous zero sequence pow
)
where p is the instantaneous real
stantaneous imaginary power and
zero sequence power has in turn a mean value or dc
component (
er is given by,
000
pVI (4
power and q is the in-
p is the instantane-
0
ous zero-sequence power. The instantaneous real and
0
,pp) and an oscillating value or ac com-
me
ce active power. The reference source current
in
ponent (0 ,pp

).
The objective of the p-q theory is to make the source
to deliver the constant active power demanded by the
load. At the s time the source should not deliver any
zero sequ
a
en
the α-β-0 frame is therefore,
*
0
*
c
c
iVV
pp
VV q
i



 

 


 


nt must be compensated,
the refeompensation current in the
is I0

(5)
Since the zero-sequence curre
rence c
itself:
zero coordinate
00c
iI

(6)
In order to obtain the reference compensation currents
in the a-b-c co
n expres
ordinates, the inverse of the transformation
given ision (2) is taken as given below,
**
0
**
**
12 10
12 1232
12 1232
ca c
cb c
ii
ii
ii


cc c 













 

(7)


The censation current for neutral is giveompn by


***
cnca cb cc
iiii  (8)
that
th the
source is not sinusoidal, this
a curreharmonic components [5]. In such a case,
th
nce of other loads on the shunt filter
pe
ing sig-
current
co three phases are designed to operate
indepetly. Each current controller determines the
In the p-q theory presented above, it is assumed
e source voltage is sinusoidal and balanced. If
voltage
nt with
nden
algorithm generates
e Phase Locked Loop (PLL) can be used to eliminate
the harmonic components in the voltage at the point of
common coupling.
The block diagram representation of the PLL circuit is
given in Figure 2. PLL is used to detect the fundamental
positive-sequence component of the voltage at the PCC
and hence the influe
rformance can be eliminated. This method is called as
modified instantaneous p-q theory which is suitable for
balanced, unbalanced and distorted source voltage condi-
tions. This modified p-q theory is followed in this work.
4. Fuzzy Adaptive Hysteresis Current
Controller
Hysteresis current controller derives the switch
nals of the inverter power switches (IGBTs). The
ntrollers of the
switching signals to its inverter bridge. The switching
logic for phase A is formulated as follows

R. PONPANDI ET AL.425
V
na
V
nb
V
nc
sin(ωt)
PI-Controller
sin(ωt-2 π/3)
1/s
sin(ωt-π/2)
sin(ωt-π/2-2 π/3)
sin(ωt-π/2+2 π/3)
X
X
V
ab
V
cb
ω
ωt
Σ
Figure 2. Phase locked loop circuit.
If upper switch is O
itc

a similar manne
derived.
ctor up and down so that it
fo

*
fa fa
iiHB
h is ON.
FF and lower
sw
If upper switch is ON and lower
switch is OFF.

*
fa fa
iiHB
In r, the switching logic for devices in
phase B and C are
The switches are controlled asynchronously to ramp
the current through the indu
llows the reference. The current ramping up and down
between the two limits is illustrated in Figure 3. When
the current through the inductor exceeds the upper hys-
teresis limit a negative voltage is applied by the inverter
to the inductor. This causes the current in the inductor to
decrease. Once the current reaches the lower hysteresis
limit a positive voltage is applied by the inverter to the
inductor and this causes the current to increase and the
cycle repeats.
The bandwidth of the hysteresis current controller is
given by [10],

2*
9d
1,
6d
ffa s1,2,3
j
mf dc f
Li
vt j
fLV Lt





(9)
dc
V
HB 
where m
f
is the modulation frequency, *
f
a
i is the
source reference current,
*
d
d
f
a
i
t represents its slope,
f
L is the decoupling inductance of the active power
is
me
dra
bhree
ity of
filter, is the DC bus voltage and

s
vt the sup-
dc
V
ply voltage.
The fixed hysteresis bandthod explained has the
wbacks of variable switching frequency, heavy inter-
ferenceetween the phases in case of tphase active
filter with isolated neutral and irregularthe modula-
tion pulse position [15]. These problems result in high
current ripples, acoustic noise and difficulty in designing
input filter. To overcome these difficulties, this paper
presents an adaptive hysteresis band current control
technique in which the hysteresis bandwidth is deter-
mined by the fuzzy logic controller.
Fuzzy control is based on the principles of fuzzy logic
[18]. It is a non-linear control method, which attempts to
apply the expert knowledge of an experienced user to the
design of a controller. Fuzzy modeling provides the abil-
ity to linguistically specify approximate relationships
between the input and desired output. The relationships
are represented by a set of fuzzy If-then rules in which
the antecedent is an approximate representation of the
state of the system and the consequent provides a range
of potential responses.
In this work, the fuzzy logic controller is used to de-
termine the hysteresis band width according to the sup-
ply voltage and the rate of change of filter current.
From Equation (7), it is noted that the hysteresis band-
width is a function of
*
d
d
f
a
i
t and


s
vt. Hence, these vari-
ables are taken as input to the fuzzy controller, an d the
hy
variables namely, NL (Negative Large), NM (Negative
steresis band width (HB) is the output. Five linguistic
Figure 3. Waveform of hysteresis current control operation
waveform.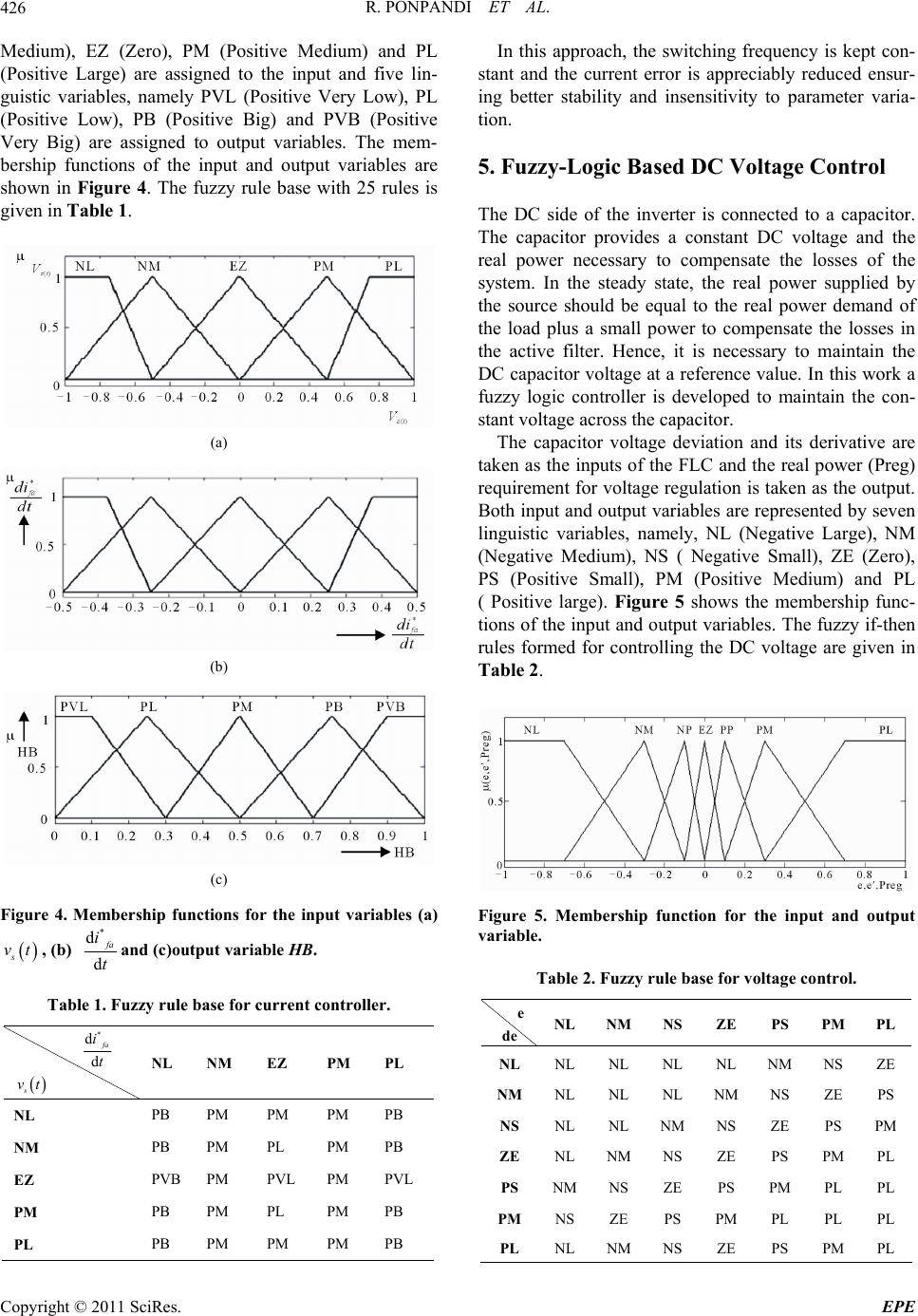

R. PONPANDI ET AL. 426
Medium), EZ (Zero), PM (Positive Medium) and PL
ssignthe (Positive Large) are aed to input and five lin-
guistic variables, namely PVL (Positive Very Low), PL
(Positive Low), PB (Positive Big) and PVB (Positive
Very Big) are assigned to output variables. The mem-
bership functions of the input and output variables are
shown in Figure 4. The fuzzy rule base with 25 rules is
given in Table 1.
(a)
(b)
(c)
Figure 4. Membership functions for the input variables (a)


s
vt, (b)
*
d
d
f
a
i
tand (c)output variable HB.
Table 1. Fuzzy rule baor current controller. se f
*
dfa i

NL NM EZ
dtPM PL

s
vt
NL PB PM PM PM PB
NM PB PM PL PM PB
EZ
PM PB PM PL PM PB
PVB PM PVLPM PVL
PL PB PM PM PM PB
In this approach swng uen keon-
stant and the currentd r-
inetter stabilityn paetea-
ti
5. Fuzzy-Logic Based DC Voltage Control
ower necessary to compensate the losses of the
by
f
, theitchifreqcy ispt c
error is
and i
appreciably re
sensitiv
duce
ram
ensu
r varig bity to
on.
The DC side of the inverter is connected to a capacitor.
The capacitor provides a constant DC voltage and the
real p
system. In the steady state, the real power supplied
the source should be equal to the real power demand o
the load plus a small power to compensate the losses in
the active filter. Hence, it is necessary to maintain the
DC capacitor voltage at a reference value. In this work a
fuzzy logic controller is developed to maintain the con-
stant voltage across the capacitor.
The capacitor voltage deviation and its derivative are
taken as the inputs of the FLC and the real power (Preg)
requirement for voltage regulation is taken as the output.
Both input and output variables are represented by seven
linguistic variables, namely, NL (Negative Large), NM
(Negative Medium), NS ( Negative Small), ZE (Zero),
PS (Positive Small), PM (Positive Medium) and PL
( Positive large). Figure 5 shows the membership func-
tions of the input and output variables. The fuzzy if-then
rules formed for controlling the DC voltage are given in
Table 2.
Figure 5. Membership function for the input and output
variable.
Table 2. Fuzzy rule base for voltage control.
eNL NMNS ZE PS PMPL
de
NL NL NL NL NL NM NS ZE
NM PS
NS NL NL NMNS ZE PS PM
PL NL NM NS ZE PS PM PL
NL NL NL NM NS ZE
ZE NL NM NS ZE PS PM PL
PS NMNS ZE PS PM PL PL
PM NS ZE PS PM PL PL PL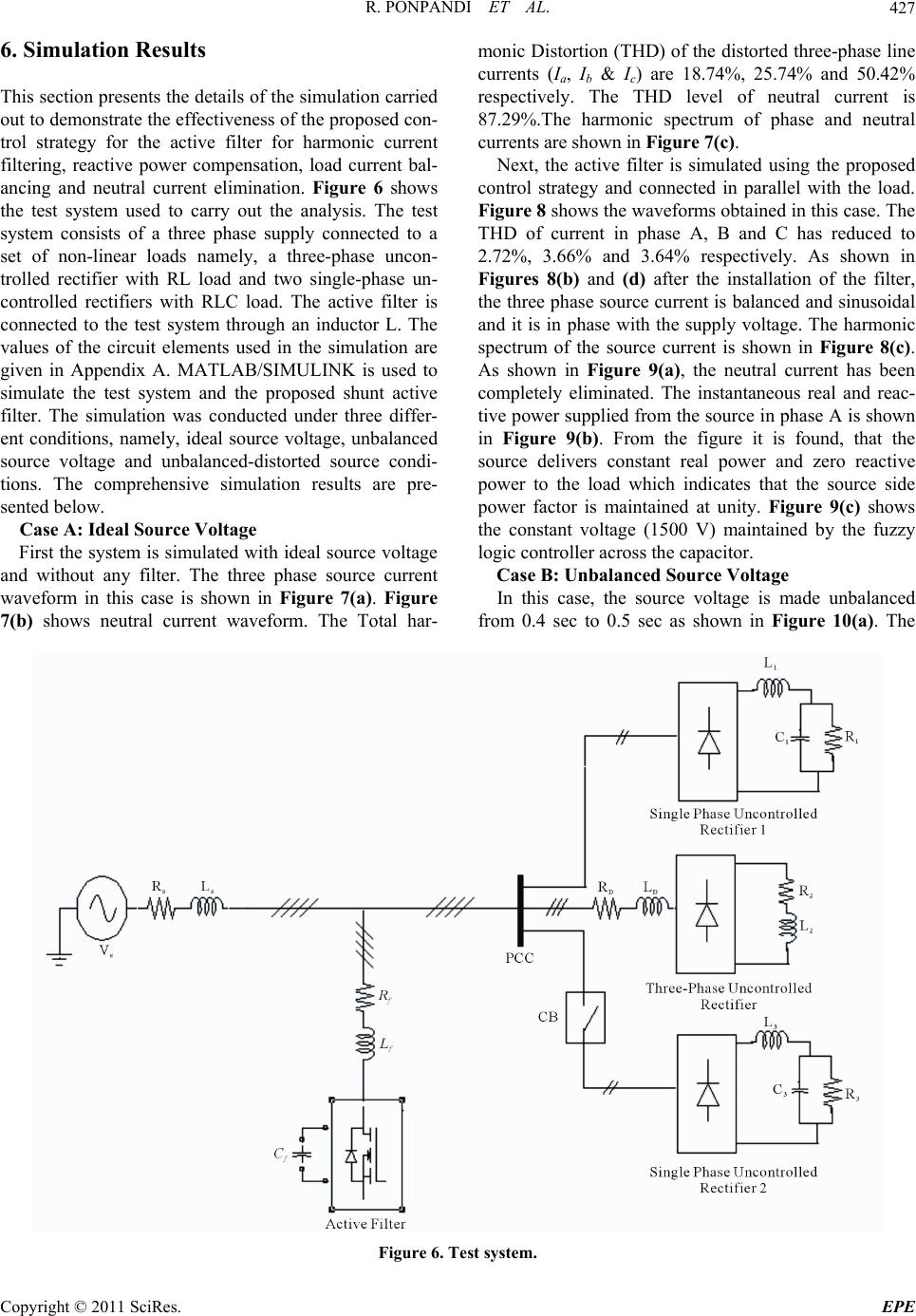

R. PONPANDI ET AL. 427
6.uon su
Thctire thtail the simul carried
oudemtrae etivs o prsed-
troatefor ac fforrm ct
filtering, reactive r compoad current-
an anuturreli ss
t the analysis. The test
upply connected to a
set of non-linear loads namely, a three-phase uncon-
ed in this case. The
TH
Figure 10(a). The
Simlati Relts
is seon psentse des ofation
t to onste thffecenesf theopo con
l strgy the
powe
tiveilter
ensation, l
haonicurren
bal
cingd neral cent mination. Figure 6how
monic Distortion (THD) of the distorted three-phase line
currents (Ia, Ib & Ic) are 18.74%, 25.74% and 50.42%
respectively. The THD level of neutral current is
87.29%.The harmonic spectrum of phase and neutral
currents are shown in Figure 7(c).
Next, the active filter is simulated using the proposed
control strategy and connected in parallel with the load.
Figure 8 shows the waveforms obtainthe test system used to carry ou
system consists of a three phase sD of current in phase A, B and C has reduced to
2.72%, 3.66% and 3.64% respectively. As shown in
Figures 8(b) and (d) after the installation of the filter,
the three phase source current is balanced and sinusoidal
and it is in phase with the supply voltage. The harmonic
spectrum of the source current is shown in Figure 8(c).
As shown in Figure 9(a), the neutral current has been
completely eliminated. The instantaneous real and reac-
tive power supplied from the source in phase A is shown
in Figure 9(b). From the figure it is found, that the
source delivers constant real power and zero reactive
power to the load which indicates that the source side
power factor is maintained at unity. Figure 9(c) shows
the constant voltage (1500 V) maintained by the fuzzy
logic controller across the capacitor.
Case B: Unbalanced Sou rce Voltage
In this case, the source voltage is made unbalanced
from 0.4 sec to 0.5 sec as shown in
trolled rectifier with RL load and two single-phase un-
controlled rectifiers with RLC load. The active filter is
connected to the test system through an inductor L. The
values of the circuit elements used in the simulation are
given in Appendix A. MATLAB/SIMULINK is used to
simulate the test system and the proposed shunt active
filter. The simulation was conducted under three differ-
ent conditions, namely, ideal source voltage, unbalanced
source voltage and unbalanced-distorted source condi-
tions. The comprehensive simulation results are pre-
sented below.
Case A: Ideal Source Voltage
First the system is simulated with ideal source voltage
and without any filter. The three phase source current
waveform in this case is shown in Figure 7(a). Figure
7(b) shows neutral current waveform. The Total har-
Figure 6. Test system.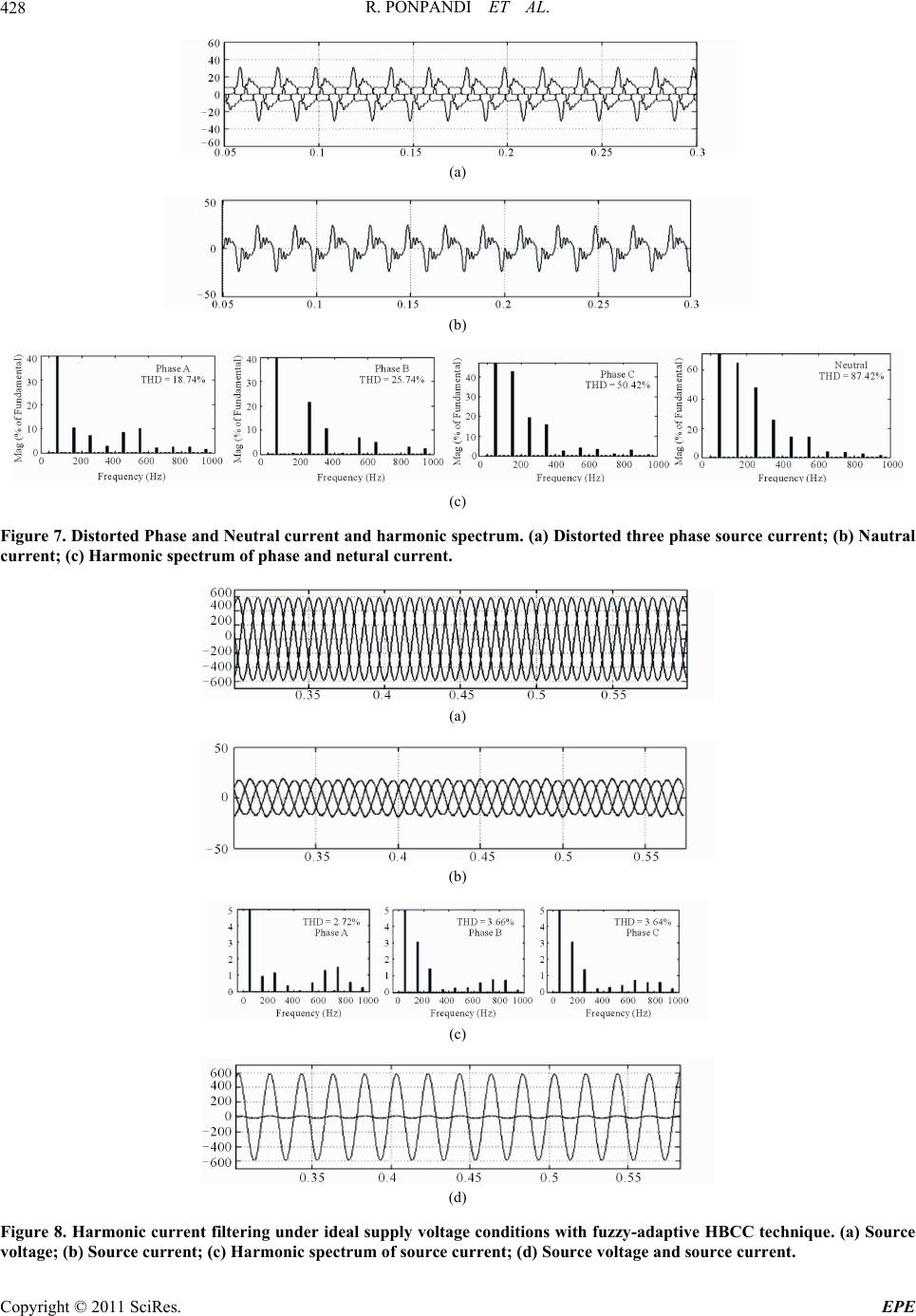

R. PONPANDI ET AL. 428
(a)
(b)
(c)
Figure 7. Distorted Phase and Neutral current and harmonic spectrum. (a) Distorted three phase source current; (b) Nautral
current; (c) Harmonic spectrum of phase and netural current.
(a)
(b)
(c)
(d)
Figure 8. Harmonic cur rent filtering under ideal supply voltage conditions with fuzzy-adaptive HBCC technique. (a) Source
voltage; (b) Source current; (c) Harmonic spectrum of source current; (d) Source voltage and source current.

R. PONPANDI ET AL.429
(a)
(b)
(c)
Figure 9. Reactive and ne utral current compensation under id eal supply voltage conditions with fuzzy-adaptive HBCC tech-
nique. (a) Nautral current; (b) Instantaneous real and reactive power; (c) Voltage across the capacitor.
(a)
(b)
Figure 10. Unbalanced source voltage and load current. (a) Unbalanced source voltage; (b) Unbalance load current.

R. PONPANDI ET AL. 430
unbalance is due to the voltage deviation in phase A. The
unbalanced load current is shown in Figure 10(b). In the
absence of the active filter, the THD level of the three
phase currents and neutral current between the time pe-
riod 0.4 sec to 0.5 sec are 20.91%, 25.74%, 50.92% and
92.06% respectively. The source current waveform and
its harmonic spectrum after installing the active filter
with modified p-q theory and the proposed control strat-
egy are given in Figure 11. In this case, the THD level
C respectively. For comparison, the filter was simulated
with general p-q theory for reference current calculation
and the compensated current is shown in Figure 12.
Since the compensation current references have nega-
tive-sequence component, the three phase compensated
source current is not sinusoidal with general p-q theory.
Also in this case, the THD value of source current after
compensation exceeds the IEEE standard limit as shown
in Table 3. This shows that the general p-q theory is not has reduced to 2.9%, 3.7% and 3.66% in phase A, B and suitable for compensation under unbalanced source
(a)
(b)
(c)
(d)
Figure 11. Harmonic current filtering under unbalanced supply voltage conditions with fuzzy-adaptive hbcc technique. (a)
Unbalanced source voltage; (b) Source current; (c) Harmonic spectrum of source current (THD for 0.4 to 0.5 sec); (d) Neu-
tral curren t .

R. PONPANDI ET AL.431
(a)
(b)
Figure 12. Harmonic current filtering using general p-q theory. (a) Load current; (b) Harmonic spectrum of load current
(THD for 0.4 sec to 0.5 sec).
Table 3. Detailed summary of source current and their THD under unbalanced source voltage.
Total Harmonic Distortion (THD) (%)
Without Filter General p-q theory Modified p-q theory
Three Phase
Balanced Voltage
(t > 0.5 sec) Unbalanced Voltage
(0.4 sec < t > 0.5) Balanced Voltage (t > 0.5 sec) Unbalanced Voltage (0.4 sec < t > 0.5) Balanced Voltage (t > 0.5 sec) Unbalanced Voltage (0.4 sec < t > 0.5)
Phase A 18.74 20.91 3.07 13.65 2.72 2.9
Phase B 25.74 25.74 4.5 11.49 3.66 3.7
Phase C 50.42 50.92 3.8 15.86 3.64 3.66
three phase source voltages are unbalanced
and distorted, source voltage contains negative sequence
component and harmonic voltage components. The dis-
torted and unbalanced source voltage, source current and
its harmonic spectrum and neural line current before the
installation of the active filter are shown in Figures
13(a)- (d). Next, the active filter is simulated with modi-
fied p-q theory for reference current calculation and with
proposed control strategy and connected in parallel with
the load. The simulation results are shown in Figure 14.
From the figure it is evident that three phase source cur-
rents are balanced and sinusoidal after the installation of
and the source side power factor is maintained at unity.
The summary of source currents and their THD level in
each phase before and after filtering are given in Table 4.
For comparison, the filter was simulated with fixed
HBCC technique and the source current waveform along
with its harmonic spectrum is shown in Figure 15. Per-
formance comparison of the filter with fixed hysteresis
band and fuzzy adaptive control strategies is given in
Table 5. From the table it is observed that the proposed
current control technique performs better than the fixed
hysteresis current control technique in reducing the har-
monics.
voltage conditions.
Case C: Unbalanced-Distorted Source Voltage
When the
the filter. Further, it is found that the source delivers
constant real power and zero reactive power to the load

R. PONPANDI ET AL. 432
7. Conclusions
This paper has presented a fuzzy logic based approach
for developing the active filter for three-phase four-wire
distribution system. Modified p-q theory was employed
for effectively computing the reference current under
non-ideal source voltage conditions. The active filter was
simulated using MATLAB/Simulink and the perform-
ance was analyzed in a sample power system with a
source and set of non-linear loads. The simulation results
show that the proposed technique is effective in current
harmonic filtering, reactive power compensation, neutral
current elimination under unbalanced load and non-ideal
source voltage conditions. Further the proposed tech-
(a)
(b)
(c)
tage condition. (a) Unbalanced and distor ted source voltage ;
d) Harmo
(d)
vol
t; (nic spectrum of source current.
Figure 13. Waveforms under unbalanced and distorted source
(b) Unbalance and distorted source voltage; (c) Neutral curren

R. PONPANDI ET AL.433
(a)
(b)
(c)
Figure 14. Harmonic current filtering under unbalanced and distorted supply voltage conditions. (a) Source current; (b
Harmonic spectrum of source current; (c) Neurral current.
)
(a)
(b)
Figure 15. Harmonic current filtering under ideal supply voltage conditions with fixed HBCC technique. (a) Source current;
(b) Harmonic spectrum of source current.

R. PONPANDI ET AL. 434
Table 4. Summary of source current THD.
THD (%)
Three Phases Without Filter With Filter
Phase A 26.35 3.38
Phase B 25.6 4.5
Phase C 61.2 4.6
Neutral 98.2 -
Table 5. Summary of source current THD for various con-
trol strategies.
THD (%)
Voltage
Control Current Control Phase A Phase B Phase C
Without Filter 18.74 25.74 50.42
Fuzzy Fixed Hysteresis 3.4 4.3 4.5
Fuzzy Fuzzy-Adaptive
Hysteresis 2.72 3.6 3.6
nique has quick response time and it keeps the switching
frequency nearly constant with good quality of filtering.
8. References
[1] B. Singh, K. Al Haddad and A. Chandra, “A Review of
Active Filters for Power Quality Improvement,” IEEE
Trans on Industrial Electronics, Vol. 46, No. 5, October
1999, pp. 960-970. doi:10.1109/41.793345
[2] L. Asiminoaei, Fr. Blaabjerg and S. Hansen, “Evaluation
of Harmonic Detection Methods for Active Power Filter
Applications,” Applied Power Electronics Conference,
Vol. 1, March 2005, pp. 635-641.
[3] K. G. Firouzjah, A. Sheikholeslami, M. R. Karami-Mol-
laei and F. Heydari, “A Predictive Current Control
method for Shunt Active Filter with Windowing Based
Wavelet Transform in Harmonic Detection,” Simulation
Modelling Practice and Theory, Vol. 17, No. 1, 2009, pp.
883-896. doi:10.1016/j.simpat.2009.02.008
[4] L. S Czarnecki, “On Some Misinterpretations of the In-
stantaneous Reactive Power p-q Theory,” IEEE Transac-
tion on Power Electronics, Vol. 19, No. 3, 2003, pp.
828-836.
[5] J. Afonso, C. Couto and J. Martins, “Ative Filters with
Control Based on the p-q Theory,” IEEE Industrial Elec-
tronics Society Newsletter, Vol. 47, No. 3, 2000, pp. 5-10.
[6] Z. Salam, T. P. Cheng and A. Jusoh, “Harmonics Mitiga-
tion Using Active Power Filter: A Technological Re-
view,” Elekrika, Vol. 8, No. 2, 2006, pp. 17-26.
[7] H. Akagi, E. H. Watanabe and M. Aredes, “The P-Q The-
ory for Active Fiter Control: Some Problems and Solu-
tions,” Revista Controle & Automacao, Vol. 15, No. 1,
2004, pp. 945-970.
[8] H. Abaali, M. T. Lamchich and M. Raoufi, “The Three
Phase Shunt Active Fiters for the Harmonics Compensa-
tion under Distorted and Unbalanced Mains Voltage
Conditions,” IEEE International Conference on Indus-
trial Technology (ICIT), Vol. 1, 2004, pp. 558-563.
[9] K. G. Firouzjaz, A. Sheikholeslami, M. R. Karami and F.
Heydari, “Predictive Current Control Method for Shunt
Active Filter with Windowing Based Wavelet Transform
in Harmonic Detection,” Simulation Modelling Practice
and Theory, Vol. 17, No. 1, 2009, pp. 883-896.
doi:10.1016/j.simpat.2009.02.008
[10] M. S. A. Al-Haddad, F. Fnaiech and L. A. Dessaint,
“Sliding Mode Control of 3-Phase 3-Wire Phase Shunt
Active Filter in the dq Frame,” IEEE Proceedings, Vol. 2,
2001, pp. 765-769.
[11] J. Rodriguez, J. Ponti, C. Silva, S. Kouro, A. Liendo and
J. Rebolleo, “Hysteresis Current Control and DTC: An
Assessment,” International Journal of Electronics, Vol.
91, No. 11, 2004, pp. 639-651.
doi:10.1080/00207210412331332871
[12] M. Kale and E. Ozdemir, “An Adaptive Hysteresis Band
Current Controller for Shunt Active Power Filter,” Elec-
trical Power and Energy Systems, Vol. 73, No. 2, 2005, pp.
113-119.
[13] A. D. Aquila and A. Lecci, “A Current Control for
Three-Phase Four Wire Shunt Active Filters,” Au ,
Vol. 44, No. 3-4, 2003, pp. 129-135.
Filters,” IEEE Transactions on Power Electronics, Vol.
12, No. 5, 1997, pp. 876-884. doi:10.1109/63.623006
tomatika
[14] L. Malesani, P. mattavelli and P. Tomasin, “High-Per-
formance Hysteresis Modulation Technique for Active
[15] M. Kale and E. Ozdemir, “An Adaptive Hysteresis Band
Current Controller for Shunt Active Power Filter,” Elec-
trical Power and Energy Systems, Vol. 73, No. 2, 2005, pp.
113-119.
[16] S. Buso, L. Malesani and P. Mattavelli, “Comparison of
Current Control Techniques for Active Power Filter Ap-
plications,” IEEE Transactions on Industrial Electronics,
Vol. 45, No. 5, 1998, pp. 722-729.
doi:10.1109/41.720328
[17] S. K. Jain, P. Agrawal and H. O. Gupta, “Fuzzy Logic
Controlled Shunt Active Power Filter for Power Quality
Improvement,” IEE Proceedings in Electrical Power Ap-
plications, Vol. 149, No. 5, September 2002, pp. 317-
328.
[18] C. Sharmeela, M. R. Mohan, G. Uma and J. Baskaran,
“Fuzzy Logic Controller Based Three-Phase Shunt Ac-
tive Filter for Line Harmonics Reduction,” Journal of
Comuter Science, Vol. 3, No. 2, 2007, pp. 76-80.

R. PONPANDI ET AL. 435
ppen
System Param
Supply phase to phase vo
Adix A
eters
ltage, frequency 415 V (rms), 50 Hz
Suppameters ly line ParRs = 1 Ω, Ls = 1 mH
Load
Filter coupling Inductance
DC Voltage Control:
Voltage
s
Sampli
Parameters
R1 = 50 Ω, L1 = 1 mH, C1 = 47 μF
R2 = 70 Ω, L2 = 37 mH
R3 = 60 Ω, L3 = 1 mH, C3 = 470 μF
RD = 0.1 Ω, LD = 3 mH
Lf = 3 mH, Rf = 0.5 Ω
1 mF
Inverter DC bus capacitor
Reference
Hysteresi
1500 V
0.5 A
2e–6 sec
Band Limit
ng Time