Journal of Signal and Information Processing, 2011, 2, 245-251
doi:10.4236/jsip.2011.23034 Published Online August 2011 (http://www.SciRP.org/journal/jsip)
Stability Conditions of Fuzzy Filter Type III
José de Jesús Medel Juárez1, Juan Carlos García Infante2, Juan Carlos Sánchez García2
1Centre of Computing Research, National Polytechnic Institute, Vallejo, México; 2Professional School of Mechanical and Elect r ical
Engineering, National Polytechnic Institute, Coyoacan, México.
Received October 12th, 2010; revised February 10th, 2011; accepted February 17th, 2011.
ABSTRACT
A digital fuzzy logic filter of type III interacts with a real model signal reference to obtain the best answer in the sen se
of minimum mean square error of the output. The key part of the filter is a fuzzy mechanism that adaptively selects and
emits answer according to the changes of the external reference signal. Based on input signal level, this fuzzy filter se-
lects the best parameter values from a set of membership in the kno wledg e base (KB), and the filter weights ar e upd ated
according to the reference signal in a natural form. With this fuzzy structure the filter reduces error. The simulation
result shows the stability of the filter. The states of the filtering process require that all of its answers are bounded by
the error criteria probab ilistically.
Keywords: Digital Filtering, Fuzzy Systems, Estimation, Stability
1. Introduction
One of the best tools used to approximate an external
process, is a recursive digital filter that adjusts dynami-
cally its parameters and weights to give the best answers
with respect to the mean square error criterion [1]. A
digital filter is a logic algorithm programmed into com-
puter software or electronic to eliminate the noise of a
system, taking specific data, identifying system or pre-
dicting a system [1,2].
The main problem in conventional filtering operation
is that it can’t classify and infer its operation levels with
respect to a changing reference system; interpreting its
external environment changes in order to select its an-
swers with the smallest error and considering different
operation levels in dynamical sense, following the natu-
ral evolution of the reference system that interacts with
the filter. In addition, a conventional filter has not a lin-
guistic description to display its answer conditions in
human readable formats, which have problems to de-
velop capacities with high dynamical changing processes
[3].
The systems related to artificial intelligent mecha-
nisms should use fuzzy tools (as fuzzy neural net and
evolutive systems) to get its own perception giving the
best decision answers, using this to solve complex prob-
lems, actualizing and adapting its perceptions and an-
swers in accordance with a reference dynamical system
[4].
The fuzzy intelligent tool as learning techniques in a
digital filtering is an option to obtain different decision
answer levels to get the optimal answers, having an in-
teraction with an external reference dynamical system,
adapting its answers to the possible changes by selecting
the best values to get the necessary convergence condi-
tions, which should have the best operation each time [5].
The main goal of this kind of filter is to have different
level answers that describe the reference system opera-
tion as natural process, using a rule set. This requires a
feedback law in order to follow the basic properties of a
desired input signal, adjusting its parameters to give a
correct solution dynamically to minimize the error crite-
rion response and updates the filter parameters [6].
In the fuzzy filter properties, there is a problem trying
to describe the stability conditions of a fuzzy system.But
using the Kharitonov [7] theory with the Routh-Hurwitz
criterion in order to get the polynomials stability, it will
be easier and it could be integrated into the fuzzy stage to
demonstrate a system correct operation.Previous work
has shown into the simulation description of the filter
stability [8,9].
With this perspective, the paper integrates the FDF
(Fuzzy Digital Filter) concept, using statistical methods
to characterize theKalman filter internal structure to give
answers with respect to the operation levels in a natural
way making a specific decision to follow the natural ref-
erence model using fuzzy logic type III [10]. The paper
shows the stability analysis for the fuzzy filter structure

Stability Conditions of Fuzzy Filter Type III 246
to establish the bounds of the filter parameters using the
Kharitonov theory with the Ruth-Hurwitz criterion.
2. Fuzzy Intelligence
The fuzzy systems obtain their basic ideas since the first
advances of fuzzy logic by Zadeh since 1965, with re-
spect to the fuzzy sets; Fuzzy systems have an important
goal the use of approximation reasoning, establishing a
relation using the fuzzy mechanism interacting with the
external process. Accord ing with this a fuzzy system has
been applied since fifteen years ago to develop new in-
telligent technologies that consider a stage that interpret
different operational levels [11].
A fuzzy system has stable operations delimiting all its
variables and answers into the knowledge base (KB) by
the process conditions; a fuzzy system has a memory of
all the answer levels given by the process. The answer
level classification is using a set of membership func-
tions; each one has a specific value in accordance with
the operation level interpretation at the input. Using
fuzzy rules the logic conn ector if, interprets the inp ut, the
fuzzy mechanism deduce the output value and the logic
connector then, selects the correct membership function
into the KB to updates a process [12].
The fuzzy system first interprets its environment
changes at its input to get a specific operation lev el of the
reference system, having a characterization of the input
signal

y
k (desired signal) into levels. Then, the
fuzzy stage choose the corresponding if-then rule to get
the membership function value

ˆ ak in order to select
the best parameter into the knowledge base, upd ating the
process to a new required condition [13].
The fuzzy mechanism shown in Figure 1 describes the
reasoning of an external real process operation (reference
model) having a set of answerslimitedinto levels. Dy-
namically the fuzzy stage interprets its input data de-
scribing the external process into different levels. The
fuzzy stage has previously the set of all the possible val-
ues that can get from its input. Then having this mem-
bership grade to deduce the answer value to be selected,
automatically makes a selection of the membership value
into the knowledge base (this has all possible answers
values that it can give), and with this new parameter
value updates the process to a new required condition [14].
The characterization of a fuzzy system into levels could
describe different kinds of process states (as low, medium
or high) in accordance with the variable (temperature,
Figure 1. The fuzzy process.
velocity or pressure). The fuzzy mechanism dynamically
gets a corresponding answer to update a process respect
to the input changes. Using the fuzzy rules in order to
obtain the input level and get the corresponding answer
value


ˆ
y
k. This process considers stable conditions
because the characterization of a system uses as limit the
frequency distribution probabilistically using a set of
membership grades (with trian gle or Gaussian functions)
to obtain the operation levels [15].
The membership function in a fuzzy system is a value
to choose with the minimum error using the actual input
level from the reference process to update the process to
a new condition. The operation levels are prev iously into
the knowledge base of the fuzzy system as in artificial
intelligence using sup ervised learning [16]. The goal of a
this kind of systems is to classify an external reference
process into grades and get the best corresponding up-
dating answer dynamically with the best signal approxi-
mation and minimizing the errors [17]. The description
of the signal into a fuzzy structure is using ranks limited
by the reference system in order to characterize the signal
levels as:
First using the logic connector IF to get the member-
ship grade of the input


y
k, second using the logic
connector THEN to get the corresponding parameter
value


ˆ
ak , third the fuzzy mechanism updates the
process to a new condition, and gets the output value
described as


ˆ
y
k with the best appr oximation.
3. Fuzzy Digital Filtering
The fuzzy filter is an intelligent filter that has two stages
basically; the conventional adaptive filter structure con-
sidering all its conditions, and the fuzzy stage integrated
to the filter structure in order to ch aracterize its operation
to get a best signal approximation by levels. This stages
integration works together minimizing the error criterion
difference having a natural signal description in accor-
dance with the reference model changes.
On the other hand, a digital filter structure without this
fuzzy stage cannot have a characterization of an external
process to have a normal operation without get an answer
into levels, making difficult to select the best signal ap-
proximation with the minimum error. Having this is dif-
ficult to interpret the input signal of the external process
and to get the best parameter value in order to update the
process with the nearest value to have a better natural
signal descripti on [1 8] .
According with this a fuzzy d igital filter is an adaptive
filter adding a fuzzy stage that classifies the input signal


y
k, into fuzzy grades to select the best filter parame-
ter value


ˆ ak from the knowledge base in order to
update the filter weights dynamically trough time to get
the best signal approximation respect to the operation

Stability Conditions of Fuzzy Filter Type III 247
level. A fuzzy filter classifiessearches and associates
information giving the corresponding answer value ac-
cording to the desired signal from the reference process
at its input. This classifies a reference process in order to
get a dynamical filter answers. The goal is to give a de-
sired operation condition each time with stable operation
because this filter uses as limit answer value the mean
square error criterion (1) as adaptive filtering, but the
fuzzy stage minimize the error difference and gets the
best signal approximation. The membership functions
(parameters value set) are limited into the knowledge
base [19].
 
 
2
:T JkE ekek
(1)
The criterion

J
k to reduce the filter error de-
scribes the mean square of the error between the desired
signal

y
k and the filter output

y
k, allows finding
the corresponding membership function that is the best
signal approximation to minimize the filter criterion [20].
The Fuzzy filter with adaptive properties has an iterative
searching methodology using the backpropagation (BP)
learning algorithm, which updates its parameters per it-
eration dynamically by degrees classifying its member-
ship functions into the knowledge base in accordance to
the difference between the desired response


y
k and
the actual filter output


ˆ
y
k described as the error

ek. The Figure 2 shows the fuzzy filter structure:The
FDF interacts with an external reference model (real
process) changes and the filter will selects the best an-
swer to approximate the signal with minimum error.
Then, the fuzzy filter has next stages [21]: The fuzzy
filter initially has the classification of the reference proc-
ess model conditions as operation levels; having the
knowledge of all the possible levels.
 It interprets the desired signal

y
k operation levels
with the error value

ek in probabilistic form using
the inference mechanism (with the logic connector if).
 It selects a corresponding membership function

ˆ ak (parameter value) from the knowledge base
(using the logic connector then according to the error
level

ek.
 The parameter value


ˆ
ak selected, updates the
filter operation, adapting automatically its weigh val-
ues to give a correct answer

ˆ
y
k, minimizing the
least mean square criterion, with the best approxima-
tion value of the desired sig na l

y
k.
 The filter emits the best answer

ˆ
y
k, describing its
responses as linguistic operational lev els and continu-
ally repeats this cycle.
This computational model described as intelligent
process may interacts with natural processes as biologic
signals, using proce ss ing elements making connect i ons to
Input
Reference
model Inferences Undating
Filter
weights Filter
answer
Automatic
Parameter
Selecti
n
Desired
signal
KB
 

ˆ ak

ˆ yk

wk

yk
Figure 2. Fuzzy filter description.
constitute an automatic updating selection to follow the
best condition of a process.
The control area
N
T is a set of answers that the filter
has with respect to all set of desired signals that the ref-
erence system emit; the Control Area (2) is into mem-
bership intervals inside the knowledge base; in accor-
dance to a filtering criterion (mean squ are error). The set
of membership function (parameters value) represents all
the correct responses into the Knowledge Base (KB),
according to an objective law, predefined by this natural
reference process, the filter inference chooses the best
correct response from the knowledge base to each refer-
ence model change [22].






2
ˆ ,
N
Tykyk

 (2)
The desired signal


y
k at the filter input is chang-
ing its operation conditions continuously, described in
levels. The filter interprets the corresponding level inter-
val and selects the best parameter value


ˆ
ak (mem-
bership function) from the knowledge base. Updating the
filter operation to give a correct response


ˆ
y
k, the goal
of the filtering process as predictor is to follow the de-
sired signal


y
k to describe the reference process into
operation grades, and then the output filter


ˆ
y
k will
be approximately the same signal.
This filtering process determines the best value to up-
date the filter conditions and give a response with the
smallest error.
4. Stability Properties
The fuzzy filtering interacting with a real process has all
its answers bounded in order to give a correct parameter
selection [23]. But the main problem to solve is the de-
scription of the stability analysis for a filter operation
with fuzzy properties having a description of its answers
into intervals. In 1978 Kharitonov made a theory for ro-
bust systems using four polynomials [7].
In accordance with the four polynomials it is possible
to have a fuzzy stability description (into levels or rank s)
using the Routh-Hurwitz criteria for lineal systems as
fuzzy filters.
If a system has the following form:
 


1
GzYz Wz   (3)

Stability Conditions of Fuzzy Filter Type III 248
where the output equation described as:

1,
:i
i
im
Yz bz


 (4)
and its characteristic equation described as:

1,
j
j
jn
Wz az



 (5)
with ,mnN
Getting from each polynomial the parameter and es-
tablishing the uncertainty values as fuzzy systems
bounded into intervals. The parameters are:


,, ,lim,lim,
nn nnn nn
aaaaa aanN (6)
From the polynomial described above in Equation (5),
in agreement to fuzzy logic parameters and the Khari-
tonov theory, we get two polynomials limits:
 
Pair odd
WzWzW z
 
(7)
Separating the pair and odd form of Equation (5) we
get the next polynomials:


24
02 4
135
135
pair
odd
Wza azaz
Wzaz azaz


  



(8)
where n
aand n a are the limit intervals of each mem-
bership function. The nominal value of each interval
,
nn
aa (that is the maximum value of the membership
function) is the parameter n
a. Having the characteristic
equation description in robust sense as:

(1)
11
(2)
22 00
,,
,,
nn
nnn n
n
nn
Wzaazaaz
aa zaa




 

 
 

 


(9)
Now the composition of the Kharitonov’s polynomials
describing the fuzzy filter stability is:
 

 

 
12
1,30 12
13
345
345 1,4
12
01 2
14
345
345 2,3
12
01 2
23
W z WzWza azaz
azazazW z
WzWza azaz
azazazW z
WzWzaazaz



















 
345
345 2,4
12
01 2
24
345
345
azazazW z
WzWza azaz
az azaz










(10)
If all of the polynomials complain the Ruth-Hurwitz
criteria, the filtering process has stability properties.
5. Simulation
For the simulation of the fuzzy filter, we integrate the
Kalman filter structure with the fuzzy stage character-
izethe filter operation, showing graphically the fuzzy
filter operation. The Kalman filter in this case uses the
identification configuration, having a dynamical parame-
ter selection to approximate the desired signal optimally.
The simulation run 1000 iterations and used the set of
membership functions deduce all the filter changes lim-
ited by the Error Criterion (1).The reference model into
the simulation is an Auto Regressive Mobile Average
(ARMA) model, which interacts with the fuzzy filter in
order to get the best answers. This has a description in
discrete states space, expressed by the fifth order differ-
ence as:
 
5
0
1
i
x
kakixkiwk

 
 (11)
The fifth order corresponds to k = 5, and its output has
the next description:





 
,,,ykxkvkxk wkk 

 (12)
where: x(k – i) is the reference model internal states se-
quence, a(k – i) the parameters sequence, w(k) the refer-
ence model noise, y(k) the desired signal from the refer-
ence model to the filter input, and v(k) the output vector
noises.
Considering the output recursive form with respect to
Equations (11) and (12):

 
y
karkwk  (13)
where:
 



wkfvk i


,

1wk,

 
vk 


2
,
ww
N 


 ,


y
k,


wk
,




[1]
:10
k
aaka

 


 
[1 ]
:10
Tk
rk yky

 

 and Equation (13)
with upper (U) and lower (L) bo u nda ries.




  
,
U
L
ykark wk
ykark wk



 (14)
Respectively, where U a and
L
a are the boundaries
corresponding to each membership function. The nomi-
nal value set of this interval


,
L
U
aa (that is the maxi-
mum value of the membership function allowed) is the
parameters vector a.
Now considering in Equation (13) the Z-transform, the
characteristic equation is:


1
0
1T
k
Wzaz z
 







 (15)
In robust sens e: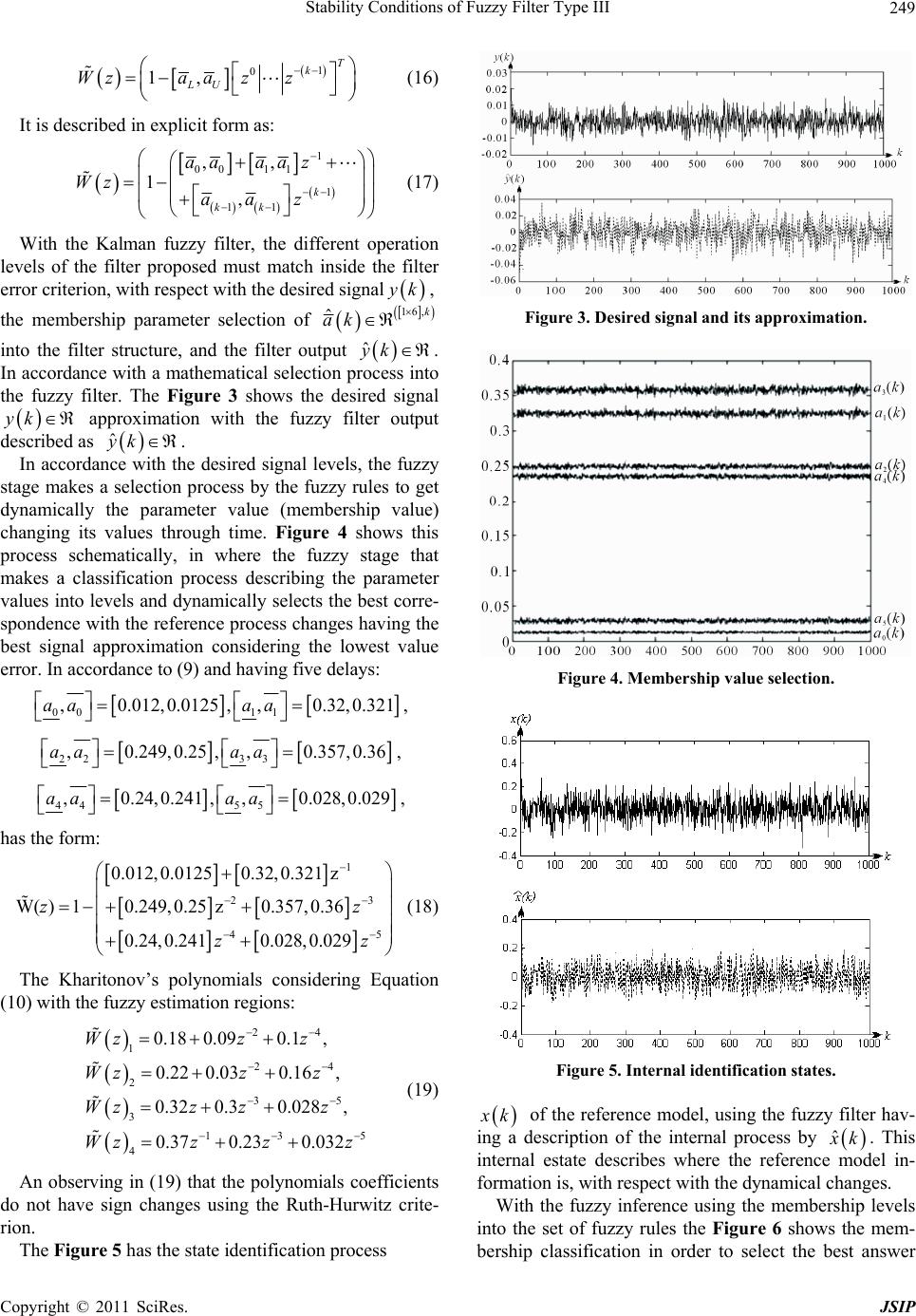

Stability Conditions of Fuzzy Filter Type III 249
 

1
0
1, T
k
LU
Wzaa zz









 (16)
It is described in explicit form as:

 
 
1
00 11
1
11
,,
1,k
kk
aa aaz
Wz aa z










 




 (17)
With the Kalman fuzzy filter, the different operation
levels of the filter proposed must match inside the filter
error criterion, with respect with the desired signal


y
k,
the membership parameter selection of

 
16,
ˆk
ak  
into the filter structure, and the filter output


ˆ
yk

.
In accordance with a mathematical selection process into
the fuzzy filter. The Figure 3 shows the desired signal

yk  approximation with the fuzzy filter output
described as

ˆ
yk .
In accordance with the desired signal levels, the fuzzy
stage makes a selection process by the fuzzy rules to get
dynamically the parameter value (membership value)
changing its values through time. Figure 4 shows this
process schematically, in where the fuzzy stage that
makes a classification process describing the parameter
values into levels and dynamically selects the best corre-
spondence with the reference process changes having the
best signal approximation considering the lowest value
error. In accordance to (9) and having five delays:

00 11
,0.012,0.0125 ,,0.32,0.321aa aa
 

  ,

22 33
,0.249,0.25 ,,0.357,0.36aa aa


  ,

44 55
,0.24,0.241 ,,0.028,0.029aa aa


  ,
has the form:





 
1
23
45
0.012,0.01250.32,0.321 z
W( )10.249,0.25 z0.357,0.36
0.24,0.241 0.028,0.029
zz
zz






  




 (18)
The Kharitonov’s polynomials considering Equation
(10) with the fuzzy estimation regions:




24
1
24
2
35
3
13 5
4
0.18 0.090.1,
0.22 0.030.16,
0.320.30.028 ,
0.37 0.23 0.032
Wzz z
Wzz z
Wzz zz
Wzzzz



 
 
 
 





(19)
An observing in (19) that the polynomials coefficients
do not have sign changes using the Ruth-Hurwitz crite-
rion.
The Figure 5 has the state identification process
Figure 3. Desired signal and its approximation.
Figure 4. Membership value selection.
Figure 5. Internal identification states.


x
k of the reference model, using the fuzzy filter hav-
ing a description of the internal process by


ˆ
x
k. This
internal estate describes where the reference model in-
formation is, with respect with the dynamical changes.
With the fuzzy inference using the membership levels
into the set of fuzzy rules the Figure 6 shows the mem-
bership classification in order to select the best answer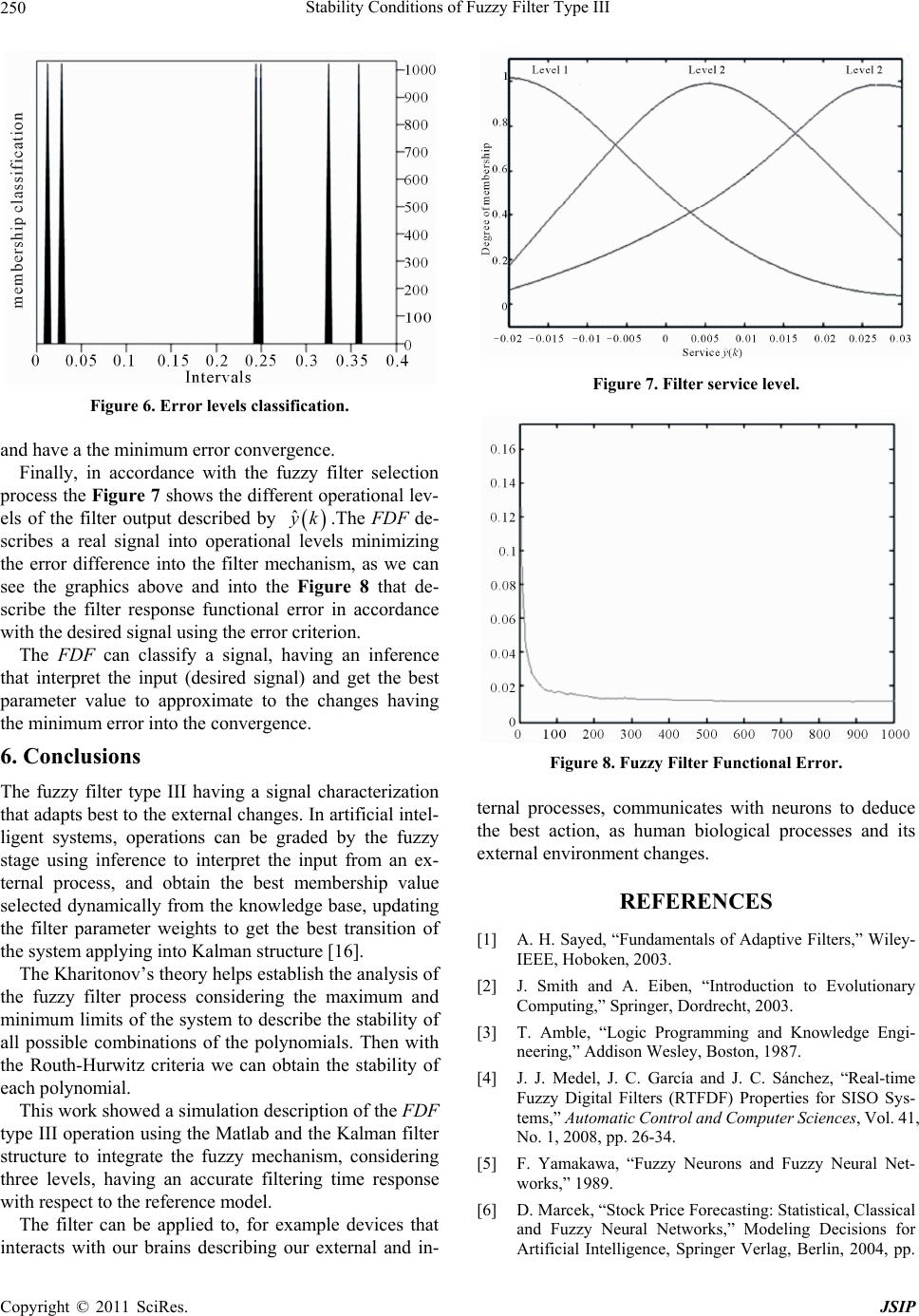

Stability Conditions of Fuzzy Filter Type III 250
Figure 6. Error levels classification.
and have a the minimum error convergence.
Finally, in accordance with the fuzzy filter selection
process the Figure 7 shows the different operational lev-
els of the filter output described by

ˆ
y
k.The FDF de-
scribes a real signal into operational levels minimizing
the error difference into the filter mechanism, as we can
see the graphics above and into the Figure 8 that de-
scribe the filter response functional error in accordance
with the desired signal using the error criterion.
The FDF can classify a signal, having an inference
that interpret the input (desired signal) and get the best
parameter value to approximate to the changes having
the minimum error into the convergence.
6. Conclusions
The fuzzy filter type III having a signal characterization
that adapts best to the external changes. In artificial intel-
ligent systems, operations can be graded by the fuzzy
stage using inference to interpret the input from an ex-
ternal process, and obtain the best membership value
selected dynamically from the knowledge base, updating
the filter parameter weights to get the best transition of
the system applying into Kalman structure [16].
The Kharitonov’s theory helps establish the analysis of
the fuzzy filter process considering the maximum and
minimum limits of the system to describe the stability of
all possible combinations of the polynomials. Then with
the Routh-Hurwitz criteria we can obtain the stability of
each polynomial.
This work showed a simulation description of the FDF
type III operation using the Matlab and the Kalman filter
structure to integrate the fuzzy mechanism, considering
three levels, having an accurate filtering time response
with respect to the reference model.
The filter can be applied to, for example devices that
interacts with our brains describing our external and in-
Figure 7. Filter service level.
Figure 8. Fuzzy Filter Functional Error.
ternal processes, communicates with neurons to deduce
the best action, as human biological processes and its
external environment changes.
REFERENCES
[1] A. H. Sayed, “Fundamentals of Adaptive Filters,” Wiley-
IEEE, Hoboken, 2003.
[2] J. Smith and A. Eiben, “Introduction to Evolutionary
Computing,” Springer, Dordrecht, 2003.
[3] T. Amble, “Logic Programming and Knowledge Engi-
neering,” Addison Wesley, Boston, 1987.
[4] J. J. Medel, J. C. García and J. C. Sánchez, “Real-time
Fuzzy Digital Filters (RTFDF) Properties for SISO Sys-
tems,” Automatic Control and Computer Sciences, Vol. 41 ,
No. 1, 2008, pp. 26-34.
[5] F. Yamakawa, “Fuzzy Neurons and Fuzzy Neural Net-
works,” 1989.
[6] D. Marcek, “Stock Price Forecasting: Statistical, Classical
and Fuzzy Neural Networks,” Modeling Decisions for
Artificial Intelligence, Springer Verlag, Berlin, 2004, pp.

Stability Conditions of Fuzzy Filter Type III 251
41-48.
[7] V. Kharitonov, “Robust stability analysis of time delay
systems: A survey,” Annual Reviews in Control, Vol. 23,
1999, pp 185-196. doi.10.1016/S1367-5788(99)90087-1
[8] L. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8,
No. 3, 1965, pp. 338-353.
doi:10.1016/S0019-9958(65)90241-XU
[9] C. L. Chen, G. Feng and X. P. Guan, “Delay Dependent
Stability Analysis and Controller Synthesis for Discrete
Time TS Fuzzy Systems with Time Delays,” IEEE
Transactions on Fuzzy Systems, Vol. 13, No. 5, 2005, pp.
630-643. doi:10.1109/TFUZZ.2005.856562U
[10] E. Onieva,V. Milanés, J. Pérez and T. Pedro, “Estimación
de un Control Lateral Difuso de Vehículos,” RIA II, Vol. 7,
No. 2, 2010, pp. 91-98. doi:10.4995/RIAI.2010.02.09U
[11] C. W. Tao and J. S. Taur, “Robust Fuzzy Control for a
Plant with Fuzzy Lineal Model,” IEEE Transactions on
Fuzzy Systems, Vol. 13, No. 1, 2005, pp. 30-41.
doi:10.1109/TFUZZ.2004.839653U
[12] E. Mamdani, “Applications of Fuzzy Algorithms for
Control of Simple Dynamic Plant,” Proceedings of the
IEEE, Vol. 121, No. 12, 1974, pp. 1585-1588.
[13] F. Gustafsson, “Adaptive Filtering and Change Detec-
tion,” John Wiley and Sons Ltd, Hoboken, 2000.
[14] K. M. Passino, “Fuzzy Control,” Addison Wesley, Boston,
1998.
[15] Ash, “Real Analysis and Probability,” Academic Press
USA, 1970.
[16] T. Tak agiand M. Sugeno, “Fuzzy Identification of Systems
and Its Applications to Modelling and Control,” IEEE
Transactions on Systems, Man, and Cybernetics, Vol. 15,
No. 1, 1986, pp. 116-132.
[17] L. Zadeh, “Maximizing Sets and Fuzzy Markoff Algo-
rithms,” IEEE Transactions on Systems, Man, and Cy-
bernetics-Part C: Applications and Reviews, Vol. 28, No.
1, 1998, pp. 9-15. doi:10.1109/5326.661086U
[18] J. García,J. Medel andL. Guevara, “Filtrado Difuso en
Tiempo Real,” Computación y Sistemas, Vol. 11, No. 4,
2008, pp. 390-401.
[19] J. García, J. Medel and J. Sánchez, “Evolutive Neural Net
Fuzzy Filtering: Basic Description,” Journal of Intelligent
Learning Systems and Applications, Vol. 2, No. 1, 2010,
pp. 12-18.
[20] S. Haykin, “Adaptive Filtering,” Prentice Hall, Upper-
Saddle River, 2001.
[21] M. Margaliot and G. Langholz, “New Approaches to
Fuzzy Modeling and Control Design and Analysis,” World
Scientific, 2000. doi:10.1142/9789812792716U
[22] B. Rajen and M. Gopal, “Neuro-Fuzzy Decision Trees,”
International Journal of Neural Filters, Vol. 16, No. 1,
2006, pp. 63-68. doi:10.1142/S0129065706000470U
[23] M. Shannon, “A Mathematical Theory of Communica-
tion,” Bell Systems Technical Journal, Vol. 27, 1948, pp.
379-423&623-656.