 Journal of Signal and Information Processing, 2011, 2, 238-244 doi:10.4236/jsip.2011.23033 Published Online August 2011 (http://www.SciRP.org/journal/jsip) Copyright © 2011 SciRes. JSIP Image Encryption Based on the General Approach for Multiple Chaotic Systems Qais H. Alsafasfeh, Aouda A. Arfoa Electrical Engineering Department, Tafila Technical University, Tafila, Jordan. Email: qsafasfeh@ttu.edu.jo, aouda@ttu.edu.jo Received April 10th, 2011; revised July 5th, 2011; accepted July 13th, 2011. ABSTRACT In the recent years, researchers developed image encryption methods based on chaotic systems. This paper proposed new image encryption technique based on new chaotic system by adding two chaotic systems: the Lorenz chaotic system and the Rössler chaotic system. The main advantage of this technique is stronger security, as is shown in the encryption tests. Keywords: Lorenz Equations, Rossler Syste m s, Image Encryption, Chaos 1. Introduction Recent researches of nonlinear dynamical systems have been increasingly based on Chaos [1]. Image encryption schemes have been increasingly studied to meet the de- mand for real-time secure image transmission over pri- vate or public networks. Conventional image encryption algorithm such as data encryption standard (DES), is not suitable for image encryption because of the special storage characteristics of an image [2] and weakness of low-level efficiency when the image is large [3].The chaos-based encryption has suggested a new and efficient way to deal with the intractable problem of fast and highly secure, image encryption. Chaotic systems have many important properties, such as the sensitive d ependence on initial conditions and sys- tem parameters, the density of the set of all periodic points and topological transitivity, etc. Most properties are related to some requirements such as mixing and dif- fusion in the sense of cryptography [4]. Matthews pro- posed a chaotic encryption algorithm in 1989 [5], since then, increasing researches of image encryption technol- ogy are based on chaotic systems [4,6-12]. These meth- ods have high-level efficiency but also weakness, such as small key space and weak security and complexity to overcome these drawbacks. This paper proposes a image encryption scheme based on combining two chaotic sys- tems (Lorenz and Rosslere) and compares the results with the other techniques. The paper is organized as fol- lows. Section 2 discusses the proposed scheme. Section 3 presents experimental results. Section 4 to Section 7 dis- cuss and examine the new scheme by applying statistical tests test also the security of the chaotic encryption is discussed. Conclusions ar e draw n in Section 8. 1.1. Lorenz Chaotic System The Lorenz equations are a fairly simple mod el in which to study chaos. xyx yrxyxz zxy z (1) The arbitrary parameters , r and b > 0 and for this example are = 10, r = 28, b = 8/3. This system of differential equations is then solved numerically using Matlab’s ode 45 Runge Kutta routine. The results are plotted in Figure 1 [12] . 1.2. Rossler Chaotic System A system of three differential equations has a simpler strange attractor than Lorenz’s. That the Rossler system has only one quadratic nonlinear xz numerical integra- tion shows this system has a strange attractor for a = b= 0.2, c = 5.7 as shown in Figure 2 [12] . xyz yxay zbzxc (2) 2. The Proposed Scheme First, most researchers used chaotic image encryption  Image Encryption Based on the General Approach for Multiple Chaotic Systems239 Figure 1. Chaotic system (time series and chaotic attractor for Lorenz system). Figure 2. Chaotic system (Chaotic attractor for rossler sys- tem). depending on only one chaotic system like Lorenz and Rossler systems. A chaotic was presented in [13], which is based on adding two chaotic systems (Lorenz and Rossler), a new chaotic system was generated as shown in Equation (3). () 20 5( xyxyz yrxyxzxay zxybzsxzc ) (3) Most of researchers agree on the following definition “chaos is aperiodic long term behavior in a deterministic system that exhibits dependence on initial condition” [12]. So to examine theses conditions we note in Figure 3 the new system has two attractors, thus satisfying the above definition. The security of Lorenz and Rossler encryption meth- ods depend on three parameters but in the proposed scheme in this paper the security level was increased to six paramete rs. Encryption Based Multiple Chaotic The goal of the step is to encrypt images by shuffling pixel values and then changing the grey scale values to create an encrypted image. The pixel values are rear- ranged using the XOR and then the grey scale values are changed using a multiple chaotic systems, and therefore after a set number of iterations (which depends on the size of the image), generated elements have been stored Figure 3. The phase plane for new system (Chaotic attrac- tor projected onto xy-plane). Copyright © 2011 SciRes. JSIP  Image Encryption Based on the General Approach for Multiple Chaotic Systems 240 within the chaotic matrix of size the same as the original image’s size. As with the other algorithms that made use of the XOR operation to encrypt, decryption is a simple matter of recreating the matrix of chaotic elements and XOR with the decrypted image matrix and therefore after a set number of iterations the original image will return. The actual procedure for encryption is shown in Fig- ure 4. Step 1. Set the key (initial condition and parameters in the acceptable intervals. 000 ,,,,,,, ,rabcyx z Step 2. Generate the first mask with the same size of image. Step 3. Perform the XOR between the chaotic mask and original image. Step 4. If the image is not encrypted generate the sec- ond mask with the same size of image. Step 5. Perform the XOR between the chaotic mask and image in Step 3. Step 6. If the image is not encrypted generate the third mask with the same size of image. Step 7. Perform the XOR between the chaotic mask and image in Step 5. Step 8. Pass the encrypted image Step 9. Pass the encryption key. Step 10. End. 3. Experimental Results Simulation results and performance analysis of the pro- posed image encryption scheme are provided in this Figure 4. Flow chart of encryption based multiple chaotic procedure. section. We take 256 × 256 size 8 bits Lena image an example Figure 5(a) its encrypted image with the en- cryption initial parameters are = (16, 45.6, 2, 0.2, 0.2, 5.7) but about initial condition we divided initial condition for each generated mask 000 ,,,,,,, ,rabcy x z 10 , 20 30 , x = (0.832345676543451, 0.523456765475432, 0.6345677654345643) as we can see, the encrypted im- age is rough-and-tu mble, unknowable and 100% obscur e of the image Figure 5(b) is the decrypted image by use the same encryption key. It can be seen that the de- crypted image is clear and correct without any distortion see Figure 5(c) to see no error between original image and decrypted image. In Figure 6 their encrypted image with sharp edge with the same encryption initial parameters and initial condi- tions. As we can see, the encrypted image is rough-and- tumble, unknowable and 100% obs cure of the image Fig- ure 6(c) is the decrypted image by use the same encryp- tion key. It can be seen that the decrypted image is clear and correct without any distortion see Figure 6(c) to see no error between original image and decrypted image. 4. Statistical Analysis Use Statistical analysis has been performed on the pro- posed image encryption algorithm, demonstrating its superior confusion and diffusion properties which strongly resist statistical attacks. This is shown by a test on the histograms of the unencrypted images and on the corre- lations of adjacen t pixels in the encrypted image. (a) (b) (c) (d) Figure 5. (a) Original image (b) encrypted image, (c) de- crypted image (d) error between original and encrypted image. Copyright © 2011 SciRes. JSIP 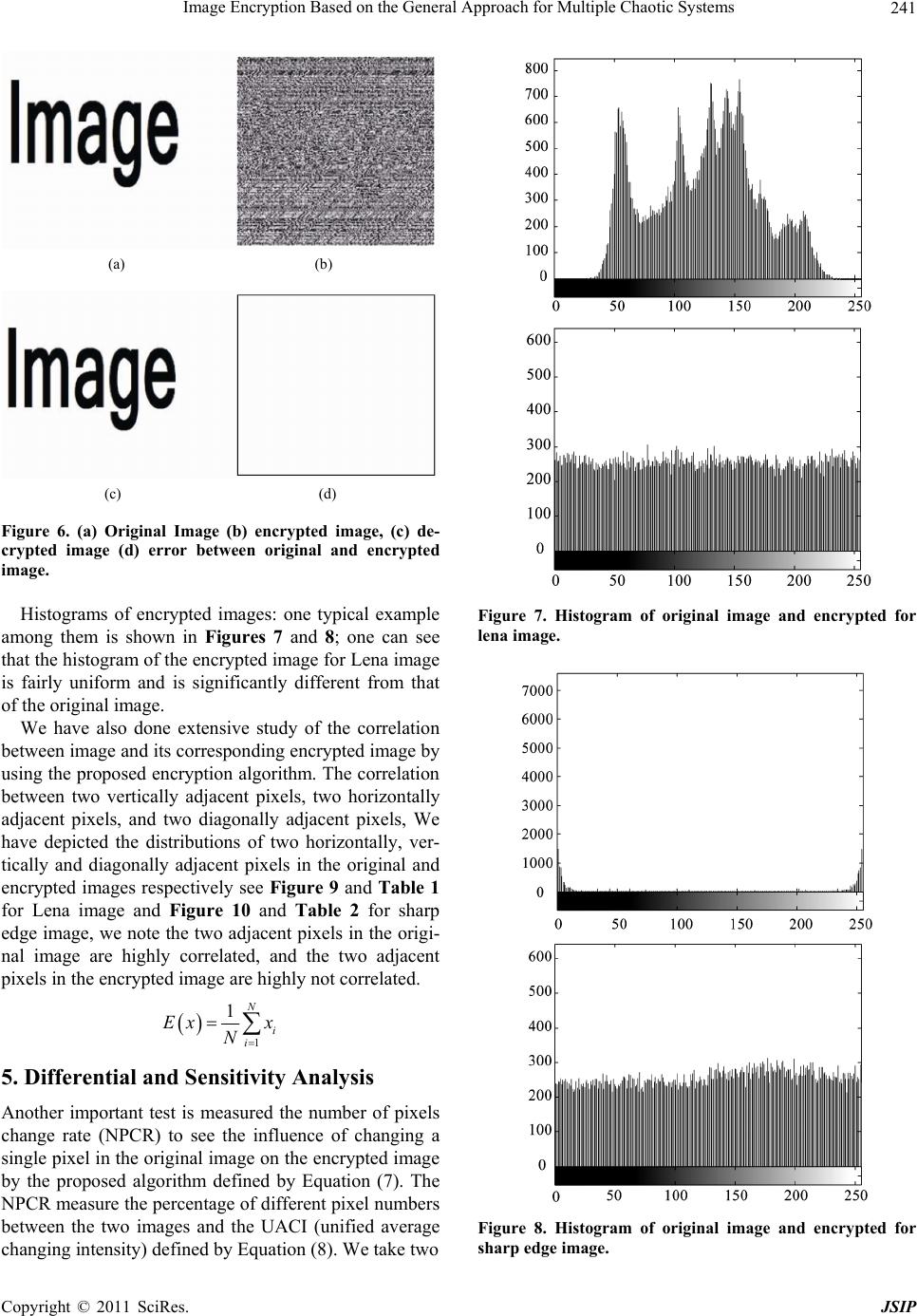 Image Encryption Based on the General Approach for Multiple Chaotic Systems241 (a) (b) (c) (d) Figure 6. (a) Original Image (b) encrypted image, (c) de- Histograms of encrypted images: one typical example am extensive study of the correlation be crypted image (d) error between original and encrypted image. ong them is shown in Figures 7 and 8; one can see that the histogram of the encrypted image for Lena image is fairly uniform and is significantly different from that of the original im a ge. We have also done tween image and its corresponding encrypted image by using the proposed en cryption algorithm. The correlation between two vertically adjacent pixels, two horizontally adjacent pixels, and two diagonally adjacent pixels, We have depicted the distributions of two horizontally, ver- tically and diagonally adjacent pixels in the original and encrypted images respectively see Figure 9 and Table 1 for Lena image and Figure 10 and Table 2 for sharp edge image, we note the two adjacent pixels in the origi- nal image are highly correlated, and the two adjacent pixels in the encrypted image are highly not correlated. 1 1N i i Ex x N 5. Differential and Sensitivity Analysis pixels Another important test is measured the number of change rate (NPCR) to see the influence of changing a single pixel in the or iginal image on the encryp ted image by the proposed algorithm defined by Equation (7). The NPCR measure the percentage of different pixel numbers between the two images and the UACI (unified average changing intensity) de fined by Equation (8). We take two Figure 7. Histogram of original image and encrypted for lena image. Figure 8. Histogram of original image and encrypted for sharp edge image. Copyright © 2011 SciRes. JSIP 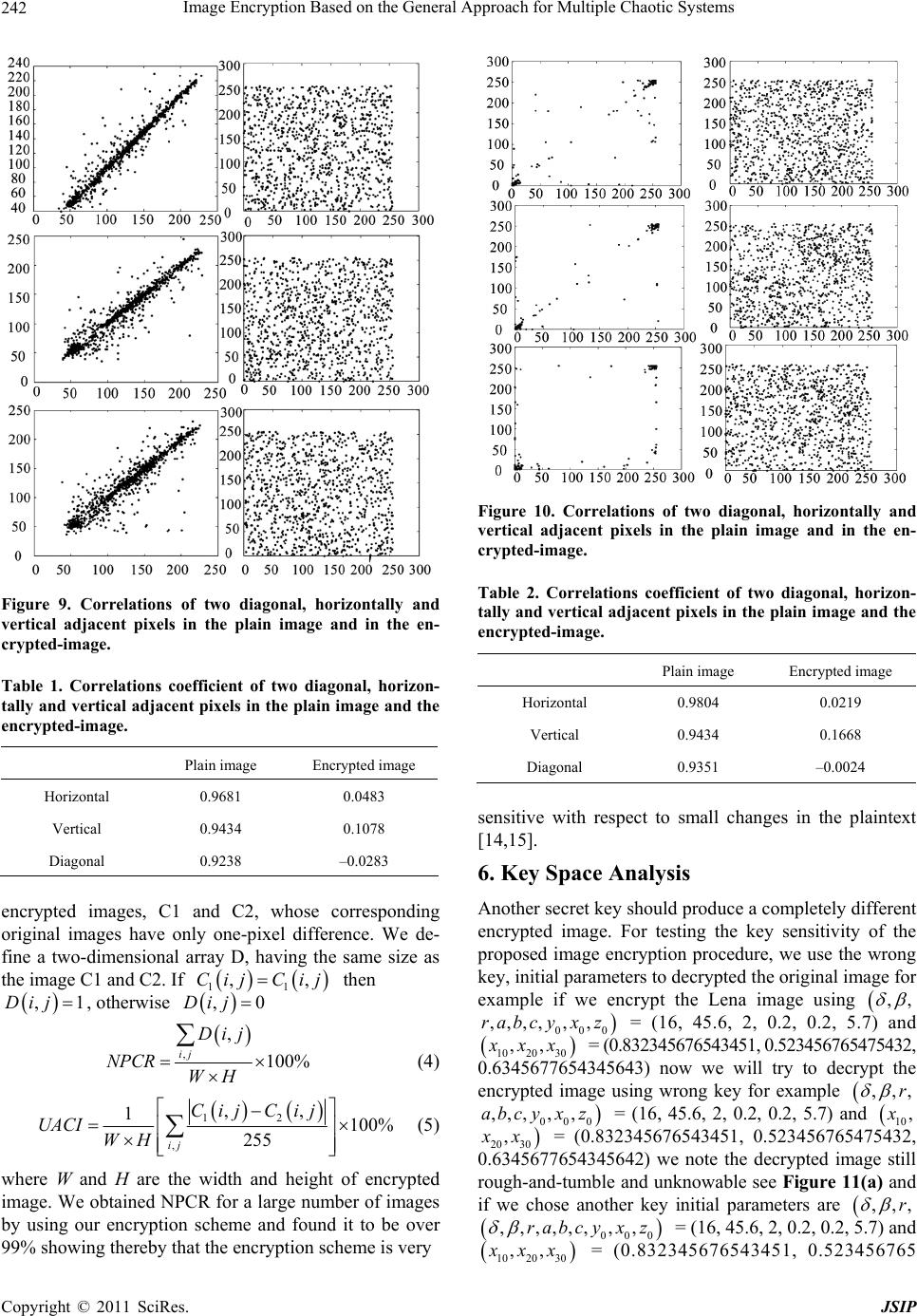 Image Encryption Based on the General Approach for Multiple Chaotic Systems 242 Figure 9. Correlations of two diagonal, horizontally and able 1. Correlations coefficient of two diagonal, horizon- Plain image Encrypted image vertical adjacent pixels in the plain image and in the en- crypted-image. T tally and vertical adjacent pixels in the plain image and the encrypted-image. Horizontal 0.9681 0.0483 Vertical 0.9434 0.1078 Diagonal 0.–0. 9238 0283 ncrypted images, C1 and C2, whose corresponding e original images have only one-pixel difference. We de- fine a two-dimensional array D, having the same size as the image C1 and C2. If 11 ,,CijCij then ,1Dij, otherwise D ,0ij , , 100% ij Dij NPCR WH (4) 12 , ,, 1100% 255 ij CijCij UACI WH (5) where W and H are the width and height of encrypted image. We obtained NPCR for a large number of images by using our encryption scheme and found it to be over 99% showing thereby that the encryption scheme is very Figure 10. Correlations of two diagonal, horizontally an able 2. Correlations coefficient of two diagonal, horizon- Pla in image Encrypted image d vertical adjacent pixels in the plain image and in the en- crypted-image. T tally and vertical adjacent pixels in the plain image and the encrypted-image. Horintal zo0.9804 0.0219 Vertical 0.9434 0.1668 Diagonal 0.9351 –0.0024 nsitive with respect to small changes in the plaintext Space Analysis duce a completely different se [14,15]. 6. Key Another secret key should pro encrypted image. For testing the key sensitivity of the proposed image encryption procedure, we use the wrong key, initial parameters to decrypted the original image for example if we encrypt the Lena image using ,, 000 ,,,,, ,rabcyx z = (16, 45.6, 2, 0.2, 0.2, 5.7 ) and 10 2030 ,, xx = (0 0.634567765 .832345676543451, 0.523456765475432, 4345643) now we will try to decrypt the encrypted image using wrong key for example ,,,r 000 ,,,,,abcy x z = (16, 45.6, 2, 0.2, 0.2, 5.7) and 10, 20 30 , x = (0.8 0.634567 32345676543451, 0.523456765475432, 7654345642) we note the decrypted image still rough-and-tumble and unknowable see Figure 11(a) and if we chose another key initial parameters are ,,,r 000 ,,,,,,, ,rabcyx z = (16, 45.6, 2, 0.2, 0.2, 5. 7) and 10 2030 ,, xx = (0.832345676543451, 0.523456765 Copyright © 2011 SciRes. JSIP  Image Encryption Based on the General Approach for Multiple Chaotic Systems Copyright © 2011 SciRes. JSIP 243 osed method and recent methods. ` Lorenz [8] Rossler [9]Logistic Map [10] New Logistic Map [7]The 3D cat map [11]One D based [8] Encryption Based Table 3. Comparison between prop Multiple chaotic Key Space 1. 158 2 16 10 2 × 24 10 45 10 36 2 53 22 75 10 Time 10.84 s 0.5 0.4 12.27 s 2 s Obscur100% <100% <100% 100% 0.33 s s e 100% 100% 100% 754329, 0.6345677654345643) the result is tumble and space should be la ty consideration, running speed of 4 unknowable as sho wn in Figure 11(b). For a secure image encrypted, the key rge enough to make the brute force attack infeasible [16]. The key of the new algorithm consists of three floating-point numbers. We note if we encrypt using 15 digits and just change the last digit the decrypted still unknown that mean we use the first 15 digits of a floating-point number, then there are 15 + 15 + 15 = 75 uncertain digits. So the possible key number is 45 10 . Moreover the parameters ,,,,,rabc are also as the secret key. An imagith such a long key space is sufficient for reliable practical use. 7. Time Analysis used e encrypted w Apart from the securi the algorithm is also an important aspect for a good en- cryption algorithm. We have measured the encryption/ decryption rate of on 256 grey-s cale images of size 256 × 256 by using the proposed image encryption scheme. The time analysis has been done on Pentium-4 with 512 MB RAM computer. The average encryption/decryption time (a) (b) Figure 11. Decrypted using wrong key for lena image. is 2 s which is less than those of the previous algo rithms. a new nonlinear chaotic algorithm, REFERENCES [1] Z. Guan, F. Hhaos-Based Image 5.08.006 Comparison between proposed method and the previous methods as shown in Table 3. 8. Conclusions This paper presents anew way of image encryption scheme have been pro- posed which uses two chaotic systems. To overcome the drawbacks of small key space and weak obscure in the current chaotic encryption methods, its structural pa- rameters and initial value are used as encryption key in chaotic. Experimental analysis demonstrates that the im- age encryption algo rithm has the advantages of large key space and high-level security, high obscure level and high speed. Finally, experimental and analytic results show that our scheme is efficient. uang and W. Guan, “C Encryption Algorithm,” Physics Letters A, Vol. 346, No. 1-3, 2005, pp. 153-157. doi:10.1016/j.physleta.200 gchien, H. W. Shieh, [2] H. H. Nien, C. K. Huang, S. K. Chan C. T. Chen and Y. Y. Tuan, “Digital Color Image Encoding and Decoding Using a Novel Chaotic R andom Generator,” Chaos Solitons and Fractals, Vol. 32, No. 3, 2005, pp. 1070-1080. doi:10.1016/j.chaos.2005.11.057 [3] Q. Alsafasfeh and A. Alshabatat, “Image Encryption hang, S. Liang and D. Li, “A New Chaotic Based on Synchronized Communication Chaotic Circuit,” Journal of Applied Sciences Re search, Vol. 7, No. 4, 2011, pp. 392-399. [4] H. Gao, Y. Z Algorithm for Image Encryption,” Chaos Solitons and Fractals, Vol. 29, No. 2, 2006, pp. 393-399. doi:10.1016/j.chaos.2005.08.110 [5] C. Fu, Z. Zhang and Y. Cao, “An Improved Image En- ng, “An Image Encryption cryption Algorithm Based on Chaotic Maps,” Third In- ternational Conference on Natural Computation, Vol. 3, Washington, 2007, pp. 24-27. [6] L. Zhang, X. Liao and X. Wa Approach Based on Chaotic Maps,” Chaos Solitons and Fractals, Vol. 24, No. 3, 2005, pp. 759-765. doi:10.1016/j.chaos.2004.09.035 [7] S. Bu and B. Wang, “Improving the Security of Chaotic Encryption by Using a Simple Modulating Method,”  Image Encryption Based on the General Approach for Multiple Chaotic Systems 244 Chaos Solitons and Fractals, Vol. 19, No. 4, 2003, pp. 919-924. doi:10.1016/S0960-0779(03)00260-1 [8] X. Wu, H. Hu and B. Zhang, “Analyzing and Improving a Chaotic Encryption Meth od,” Chaos Solit ons and Fracta ls, Vol. 22, No. 2, 2004, pp. 367-373. doi:10.1016/j.chaos.2004.02.009 [9] G. Chen, Y. Mao and C. K. Chui, “A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps,” Chaos Solitons and Fractals, Vol. 21, No. 3, 2003, pp. 749-761. doi:10.1016/j.chaos.2003.12.022 [10] F. Chiaralu ce , L. Ci ccar elli, E. G am bi, P . Pi erleo ni and M . Reginelli, “A New Chaotic Algorithm for Video Encryp- tion,” IEEE Transactions on Consumer Electronics, Vol. 48, No. 4, 2002, pp. 838-844. doi:10.1109/TCE.2003.1196410 st Image Encry Y. Zou and B. Zhang, “An “A New Chaotic Attractor [11] K. Wong, B. Kwok and W. Law, “A Faption Scheme Based on Chaotic S tandard Map,” City University of Hong Kong, Hong Kong. [12] L. Wang, Q. Ye, Y. Xiao, Image Encryption Scheme Based on Cross Chaotic Map,” Congress on Image and Signal Processing, Sanya, 27-30 May 2008, pp. 27-26. [13] Q. Alsafasfeh and M. Alarni, from Lorenz and Rossler Systems and Its Electronic Ex- perimental Implementa tion,” Circuits and System s, V ol. 2 , No. 2, 2011, pp. 101-105. doi:10.4236/cs.2011.22015 [14] T. Ga and Z. Chen, “Image Encryption Based on a New Total Shuffling Algorithm,” Chaos Solitons & Fractals, Vol. 38, No. 1, 2008, pp. 213-220. doi:10.1016/j.chaos.2006.11.009 [15] N. K. Pareek , V. Patidar and K. K . Sud, “Image Encryption Using Chaotic Logistic Map,” Image and Vision Computing, Vol. 24, No. 9, 2006, pp. 926-934. doi:10.1016/j.imavis.2006.02.021 [16] V. Patidar, N. K. Pareek and K. K. Sud, “A New Substi- tution-Diffusion Based Image Encrypete Using Chaotic Standard and Logistic Maps,” Communications in Non- Linear Science and Numerical Simulation, Vol. 14, No. 7, 2009, pp. 3056-3075. doi:10.1016/j.cnsns.2008.11.005 Copyright © 2011 SciRes. JSIP
|