Journal of Applied Mathematics and Physics
Vol.05 No.01(2017), Article ID:73269,9 pages
10.4236/jamp.2017.51003
Effect of Inlet Velocity on the Crude Oil Coking and Gas Phase Formation in a Straight Pipe
Dhamani Fouzia, Tae Seeon Park*
School of Mechanical Engineering, Kyungpook National University, Deagu, Republic South Korea




Received: October 26, 2016; Accepted: December 28, 2016; Published: January 4, 2017
ABSTRACT
A comparative numerical study is conducted to evaluate the effect of inlet velocity on the gas-liquid-solid phase change, the separation of phases and the coke formation. The numerical procedure is constructed within the Eulerian framework in which the liquid phase is treated as a continuous phase while gas and solid are both considered as dispersed phases. The simplified reaction net of crude oil is used in order to predict the thermal cracking of the crude oil. The temperature distribution, flow field, liquid?gas phase separation, and coke formation are predicted and discussed for different inlet velocities. The information predicted by the CFD model can be utilized in the optimal design of industrial fired furnaces.
Keywords:
Crude Oil Fouling, Petroleum Thermal Cracking, Preheater Coking

1. Introduction
Oil companies worldwide are forced by the strict environmental policies to increase their focus on the efficient utilization of energy. In this perspective, the efficiency of the thermal transfer to heat crude oil in heat exchanger equipment is very important, but it is often altered by coke deposition inside the process pipes. This coke layer causes progressively high tube metal temperatures (TMTs), in turn, promoting coke formation. As the TMTs get close to the tube metallurgical temperature limit, the furnace must be shut down to remove coke which leads to increased production and maintenance costs, and requires better understanding and control.
Crude oil fouling is a very complex phenomenon that occurs due to the simultaneous activities of several chemical and physical mechanisms. Fouling may be triggered by a variety of reaction pathways depending on crude composition and process condition, so the understanding of the heat transfer and thermal reaction phenomena is helpful for the fine-tuning and optimization of modern furnace design. Since the oil is composed of a complex mixture of hydrocarbons, many of which unknown, it is difficult to predict the real reactions that occur for each real chemical species. Away to circumvent this problem is by considering that the feed molecules can have its behavior represented by a small number of representative molecules, called pseudo-components.
Kijseoglu and Phillips [1] presented three kinetic models with a group of pseudo-components for catalytic hydrocracking of Athabasca bitumen. The reaction rate constants were represented by an Arrhenius type expression.
Soza et al. [2] developed a numerical model for single-phase flow inside cylindrical ducts applied to petrochemical fired heaters. They studied the operational conditions which might minimize coke formation due to the thermal cracking of the feed. Li et al. [3] and Fontoura [4] attempted to model the thermal cracking and phase change.
In this paper, a comparative multi-phase CFD model is developed for predicting the phase change and reactions for different inlet velocities to show the effect of increasing velocity on the phase separation and coke formation inside the straight pipe. Eulerian framework is used in which the liquid phase is treated as a continuous phase while gas and solid are both considered as dispersed phases. The flow and thermal field coupled with the coke formation are discussed.
2. Mathematical Model Development
2.1. Thermal Cracking Kinetic Model
Based on the previous study [1], the complete kinetic model adopted is the following Figure 1.
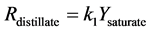
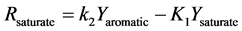

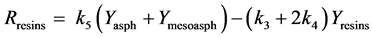
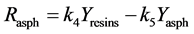
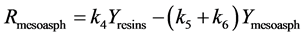
Figure 1. Kinetic net of the thermal cracking and phase change of petroleum.
Here Ri.
Here Yi and k1?6 are the source term, mass fraction and reaction rate constants of pseudo-component I respectively.
The interconversion reactions of mesoasphaltenes and asphaltenes with resins are considered to have the same reaction rate constant as k4 and k5 [3]. All the reaction rate constants are given by Arrhenius equations as:
 (1)
(1)
A is the pre-exponential factor and B is the activation energy. Details regarding the reaction parameter can be found in the previous work [3]. The reactions for phase change (Reaction 1) and coke formation (Reaction 6) involves interphase transfer, so they are introduced as source terms of continuity equations. Other reactions only occur within the liquid phase, and so are introduced as source terms of mass fraction transfer equations; the first term is not taken in consideration in the steady flow;
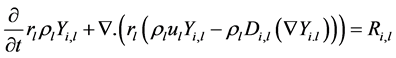 (2)
(2)
Di,l represents the kinematic diffusivity of pseudo-component i in the liquid phase and can be approximated by the kinematic viscosity in turbulent flow [5], (Sc = 1)
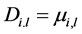
2.2. Turbulence Modeling
Turbulence field is solved using phase dependent turbulence models in which a single turbulence model is used the continuous phase and zero equations models for the dispersed because other models are not considered to be appropriate.
The standard κ-ε turbulence model is employed to model the turbulence field in the continuous phase; the values of κ and ε come directly from the differential transport equations for the turbulence kinetic energy and turbulence dissipation rate:
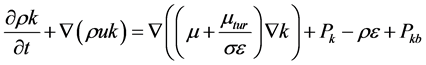 (3)
(3)
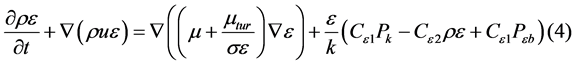 (4)
(4)
where Cε1, Cε2, σκ, and σε are constants, Pκb and Pεb represent the influence of the buoyancy force, and Pκ is the turbulence production due to viscous forces [5].
3. Computational Domain and Boundaries Conditions
As shown in Figure 2, horizontal cylindrical geometry of 18 m in length and 0.152 m in diameter is constructed to represent a segment of fired furnace tube. The grids near the tube wall are refined in order to consolidate the calculation in the boundary layer region. The computation domain has 1.5 × 106 cells. Mesh
Figure 2. Geometry model and mesh generation.
independence studies are performed to establish the effect of mesh size on the calculated results.
In order to evaluate the effect of oil velocity on phase change and coke formation, five different inlet velocities are imposed. A comparative simulations are conducted with Arabian light crude oil as domain fluid, inlet mass fractions can be found in the previous work [1]. The oil temperature is 673 K at the beginning of the tube and there is only liquid phase present and same for all cases.
The outlet boundary is specified as average static pressure of atmospheric pressure with pressure profile blend of 0.5 over whole outlet.
Constant temperature is imposed at the tube wall, Twall 873 K. A no-slip wall boundary condition is specified for the liquid phase and a free slip wall boundary condition for the vapor and solid phases (Figure 3).
4. Results and Discussion
4.1. Temperature Field
It can be observed from the liquid temperature profiles in Figure 4 that the higher temperatures of the liquid are present near the walls due to the heat received and a gradual increase of bulk oil temperature in the flow direction is evident, with the same tube wall temperature, and as the velocity increase, the liquid phase temperature decrease and this is can be explained by the short time residence inside the pipe.
4.2. Separation and Gas Formation
As shown in Figure 5(a), the gas being formed and rising quickly to the upper part of the tube, this accumulation of gas phase in the upper domain is a consequence of gravity effect, indicating the phase separation thus the implemented free-surface model succeeds in modeling the phase separation and capturing the gas?liquid interphase.
The gas superficial velocity profiles at the vertical direction are presented in Figure 5(b), we can see that the gas superficial Velocity reach the maximum value near the tube outlet and show an asymmetric behavior which can be explained by the fact that the gas phase is accumulating in the upper domain and this is already observed in Figure 5(a), where the gas superficial velocity stream
Figure 3. Boundary conditions of the computational domain.
Figure 4. Liquid phase temperature profile for different inlet velocities.


Figure 5. Gas superficial velocity profile for different inlet velocities.
lines are changing direct ion to reach the upper domain. We noticed that this behavior disappear as inlet velocity increase and straight streamline appear instead. From The gas superficial velocity profile, it is observed that as velocity increase, the superficial gas velocity decrease in magnitude, however this difference is not observed when the velocities are close, thus the effect of liquid inlet velocity on the gas superficial velocity appear only for a considerable difference.
The gas velocity is smaller in magnitude compared with those of the continuous phase.
Figure 6, show the effect of inlet velocity on the gas volume fraction, As the inlet velocity increase the gas volume fraction decrease, and this is can explained by the short time resident inside the pipe, the liquid is not heated enough and the gas formation temperature is not reached.
The gas volume gradient at tube outlet is also presented in Figure 7, a strong gradient in the upper domain is observed as discussed in the previous section, as the inlet velocity increase the gas volume gradient is decreasing and distribute symmetrically near the outlet wall. The symmetric distribution means that the buoyancy effect is not active because of the small difference between phase densities, and the gas particles is not heated enough to flow and reach the upper domain.
As shown in Figure 8, as the gas phase appears in the tube, the streamlines near the centerline of the tube waves in radial direction, and a rotational flow is also predicted, this can be caused by the effect of the strong pressure gradient induced by the gas formation; this wavy motion is not observed for all cases, as velocity getting higher, this streamline behavior disappear. It can be observed that liquid velocity near the centerline exceeds the inlet velocity, pressure increase induced by gas phase is expected to speed up the liquid flow. In addition, liquid velocity near the centerline of the tube is far above that near the tube wall as a result of boundary layer distribution.
4.3. Coke Formation
The coke amount accumulates as the oil flows forward. It is observed that the coke show same behavior as gas and accumulate in the upper domain Figure 9(a), as we know coke is the result of crude oil thermal cracking process there-
Figure 6. Gas volume fraction profile for different inlet velocities.


Figure 7. Gas volume fraction gradient profile at outlet.
Figure 8. Streamline profiles of liquid crude oil at Tb = 673 K and inlet velocity of 2 m/s.


Figure 9. Coke formation on the wall at liquid crude oil temperature Tb = 673 [K] and inlet velocity of 2 m/s.
fore it increase with temperature and in that region where the coke accumulate we already observed a higher gas phase holdup which enhanced the convective heat transfer therefore more heat is transferred from the tube wall to the liquid phase and cause high coke formation. For a high inlet velocity, the coke amount decrease as shown in Figure 9(b).
As expected, an increase in velocity has effect on the coke deposition of increasing the wall shear stress leading to a removal process; however in our study the coke amount is decreasing for the same reason as gas decrease.
5. Conclusion
In this work, a comparative study is conducted to predict the effect of inlet velocity on the phase change and coke formation inside the tubes. The calculations are performed by means of CFD. The thermal cracking kinetic model is validated against the work of Souza et al. for a single phase and the work of Li et al. for a multiphase flow. The phase change and the coke formation are predicted for a different inlet velocities. Asymmetric behavior of the two-phase flow field is observed due to gravity effect. The effect of velocity on coke formation is predicted and well discussed, less coke formation rate for higher velocity and same effect is observed for gas volume fraction. The information predicted by the CFD model can be utilized in the optimal design of industrial fired furnaces.
Cite this paper
Fouzia, D. and Park, T.S. (2017) Effect of Inlet Velocity on the Crude Oil Coking and Gas Phase Formation in a Straight Pipe. Journal of Applied Mathematics and Physics, 5, 17-25. http://dx.doi.org/10.4236/jamp.2017.51003
References
- 1. Kijseoglu, R. and Phillips, C.R. (n.d.). Hydrocracking of Athabasca Bitumen Kinetics of Formation of Gases.
- 2. Souza, B.A., Matos, E.M., Guirardello, R. and Nunhez, J.R. (2006) Predicting Coke Formation Due to Thermal Cracking inside Tubes of Petro-chemical Fired Heaters Using a Fast CFD Formulation. Journal of Petroleum Science and Engineering. https://doi.org/10.1016/j.petrol.2005.11.013
- 3. Li, X.-G., Zhang, L.-H., Zhang, R.-Y., Sun, Y.-L., Jiang, B., Luo, M.-F. and Li, X.-G. (2015) CFD Modeling of Phase Change and Coke Formation in Petroleum Refining Heaters. Fuel Processing Technology, 134, 18-25. https://doi.org/10.1016/j.fuproc.2015.03.005
- 4. Fontoura, D.V.R., Matos, E.M. and Nunhez, J.R. (2013) A Three-Dimensional Two- Phase Flow Model with Phase Change inside a Tube of Petrochemical Pre-Heaters. Fuel. https://doi.org/10.1016/j.fuel.2012.09.065
- 5. ANSYS CFX-Solver Theory Guide. (n.d.). http://www.ansys.com







