ABSTRACT

Mathematical solutions predict abstract conditions that indicate limits or bounds for physical processes. Generally, experimental verifications and phy- sical observations on physical processes validate the mathematical predictions. Sometimes these predictions lead to new theories and concepts that form basis of better understanding of the natural processes. Gravitational interactions between bodies are natural physical processes. A smaller body moves under the influence of gravity, due the gravitational effect of another large body. Newton’s classical gravitational theory addresses the interactions at low velocities. Einstein’s general relativity provides firm basis for gravitational interactions. Observations over past 100 years prove the mathematical precision and predictions of general relativity. Einstein’s special relativity forms the foundation of quantum physics. In this paper, the author applies concepts of special relativity to classical two body Newtonian gravitational problem. The study predicts a new mathematically viable condition that when a body moves at a specific velocity derived in this paper, the total energy of the moving body is zero. The specific velocity is a constant. At velocities far less than specific velocity, the total energy is negative and is equal to classical value of half the potential energy. At velocities, greater the specific velocity the total energy is positive. The specific velocity condition also enables determination of specific mass of gravitating body, as well as the specific distance of the moving body from gravitating body, at which the total energy of moving body is zero.

Keywords:

Classical Gravitation, Special Relativity, Total Energy, Gravitational Energy, Specific Velocity

1. Introduction

Mathematics is the language of Nature. To understand physical processes mathematics is essential. Mathematics enables derivation of theoretical conditions like limits or bounds for physical processes creating breakthroughs in human knowledge [1]. Many mathematically viable limits appear to be abstract. Experimental verification of such limits leads to new concepts and theories. There are many examples where mathematics played crucial role. Newton’s gravitational law, Coulomb’s law, Maxwell’s equations, Planck’s radiation theory, Lorentz’s transformation equations, Einstein’s theory of special relativity, Einstein’s theory of general relativity, de Broglie’s matter wave concept, Schrödinger’s wave equation, Dirac’s operators are a few examples in physics that changed human perception of natural physical processes. [2]. In the context of gravity, Chandrasekhar’s limit [3] and Zwicky’s prediction of dark matter [4] are two such examples apart from the many validated predictions of general relativity [5]. Special relativity [5] has played a crucial role in development of quantum theory of matter and radiation. Although general relativity fully addresses the ubiquitous gravity, adoption of concepts of special relativity to classical gravitational results is not a mathematically invalid proposition. In this paper, the author adopts this approach at an elementary level and finds that a new mathematically valid theoretical prediction evolves in the case of two-body gravitational interaction.

2. Application of Concepts of Special Relativity to Results of Classical Theory of Gravity

Let us consider the case of gravitational interaction between two bodies in which the smaller body moves towards the larger gravitating body. Let the rest mass of smaller body be and its velocity be. Let the rest mass of the gravitating body be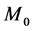. Let the distance between the two bodies be. Newton’s gravitational law [2] gives the velocity of smaller body from the relation,

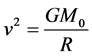(1)

where is the universal gravitational constant.

Let us define,

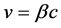(2)

where is the speed of light in vacuum and is the ratio of the velocity to the speed of light, such that.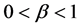

From special relativity [5], we have

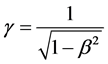(3)

where 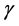is the Lorentz factor.

By squaring on both sides of Equation (3) and rewriting, we get

(4)

By substituting for 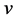from Equation (2) in Equation (1), we get

(5)

By substituting for 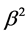from Equation (4) in Equation (5) and rewriting, we get

(6)

We know that LHS of Equation (6) is the factor for kinetic energy in special relativity, given by

(7)

where is the kinetic energy of moving body.

Substituting for from Equation (7) in Equation (6), we get a new mathematical expression for kinetic energy as

(8)

where is the potential energy of the moving body given by [2],

(9)

Equation (8) gives mathematically valid relation between the kinetic energy and potential energy of the moving body. To validate the correctness of this new relation, let us consider the case when the velocity is far less than the speed of light, i.e.. In this low velocity range, the Lorentz factor from Equation (3) is. For the value, Equation (8) should give kinetic energy-po- tential energy relation that satisfies classical gravitational theory for low velocities and the substitution gives the relation

(10)

Equation (10) meets the classical condition.

Let us examine the total energy of the moving body. The total energy is the sum of potential and kinetic energy.

(11)

where is the total energy.

By substituting for from Equation (8) in Equation (11), we get the expression for total energy in terms of, as

(12)

Let us consider the situation leading to zero total energy of the moving body. From Equation (12), we note that for to be zero, either must be zero or the expression in the bracket must be zero. In the case of two-body system considered, cannot be zero. Hence, the expression in bracket must be zero. Thus, we get the condition required in the form of an equation in terms of as follows.

(13)

By rewriting Equation (13), we get the following quadratic equation in terms of.

(14)

By solving Equation (14), we get the solution for giving the specific Lorentz factor

(15)

By substituting the value for from Equation (15) in Equation (3), and solving for, we get the specific as

(16)

By substituting the value for from in Equation (16) and Equation (2), and solving for , we get the specific velocity as

(17)

3. Results and Discussion

Equation (17) is the outcome of the present study. It states that the specific velocity is a constant in any gravitational interaction when the total energy of moving body is zero. It is independent of the properties of gravitating body as well as the moving body. It is a pure mathematical condition obtained through the derivation.

We can observe from Equation (12), that until the moving body reaches the specific velocity, its total energy is negative, at specific velocity, its total energy is zero and for velocity more than the specific velocity, its total energy is positive. This result is evident from the following discussion.

From Equation (12), we get the ratio of total energy to gravitational potential energy as.

From this expression, we obtain values of for different values of determined from Equation (3) for different values of. Table 1 gives these calculated values of for different values.

As is always negative as per Equation (9), a positive value for ratio of in Table 1 indicates negative total energy and vice versa.

Figure 1 shows the variation of ratio of total energy to potential energy with the ratio of velocity of the moving body to speed of light for the values listed in Table 1.

We may make the following observations from Figure 1 and Table 1.

a) When is near zero, the ratio of total energy to potential energy is equal to 0.50. The corresponding total energy is

b) When is 0.78615, the ratio of total energy to potential energy is equal to zero. The corresponding total energy is

c) When is more than 0.80, the ratio of total energy to potential energy is equal to −0.04. The corresponding total energy is

d) When is 0.90, the ratio of total energy to potential energy is equal to −0.60. The corresponding total energy is

e) When is 0.99, the ratio of total energy to potential energy is equal to −5.21. The corresponding total energy is

The values in Table 1 and trend in Figure 1 indicate that the total energy will be positive and increases to very large values as the velocity of the moving body approaches the speed of light.

Equation (17) further enables us to get the specific distance, , at which total energy is zero for a given gravitating mass. By substituting for the value for specific velocity from Equation (17), in Equation (5) we get,

(18)

Similarly, we get the specific gravitating mass, , at which the total energy is zero for a given distance. By substituting the value for specific velocity from Equation (17) in Equation (5), we get,

(19)

4. Conclusion

The present study of two-body classical Newtonian gravity with the help of special relativity, gives a condition that predicts a constant specific velocity equal to for the moving body. At the specific velocity, the total energy of the moving body is zero. When the body moves at velocity less than specific velocity, the total energy is negative. At very low velocities, the total energy is negative and is half the potential energy of the body as in classical theory of gravity. At velocities more than the specific velocity, the total energy is positive and can reach very high values when the velocity approaches the speed of light. The condition also enables determination of specific mass of the gravitating body, as well as specific distance of moving body from gravitating body, at which the total energy of moving body is zero.

Acknowledgements

The author gratefully acknowledges the permission granted by the management of M/s BGR Energy Systems Limited, Chennai, India to publish this work.

Cite this paper

Murthy, T.V.B.S.S. (2017) Derivation of Specific Velocity of Body Moving under Gravity with Zero To- tal Energy. Journal of Applied Mathematics and Physics, 5, 1-6. http://dx.doi.org/10.4236/jamp.2017.51001

References