Modern Economy, 2011, 2, 691-700
doi:10.4236/me.2011.24077 Published Online September 2011 (http://www.SciRP.org/journal/me)
Too Risk-Averse for Prospect T h e o ry?
Marc Oliver Rieger1, Thuy Bui2
1University of Trier, Trier, Germany
2Project Finance Department, Vingroup, Ha Noi, Vietnam
Received May 4, 2011; revised June 25, 2011; accepted July 12, 2011
Abstract
We observe that the standard variant of Prospect Theory cannot describe very risk-averse choices in simple
lotteries. This makes it difficult to accommodate it with experimental data. Using an exponential value func-
tion can solve this problem and allows to cover the whole spectrum of risk-averse behavior. Further evidence
in favor of the exponential value function comes from the evaluation of data from a large scale survey on
preferences over lotteries where the exponential value function produces the best fits. The results enhance
the understanding on what types of lotteries pose potential problems for the classical value function.
Keywords: Cumulative Prospect Theory, Decisions under risk, Risk-Aversion, Probability Weighting, Value
Function
1. Introduction
Imagine you are faced with the following gamble: with a
probability of 90% you win 100 Euro, otherwise you win
only 10 Euro. Which safe amount of money would be
equally as good for you as participating in the gamble?
Obviously, depending on your risk attitudes you could
choose any amount between 10 and 100 Euro. If you are
risk-averse, you will choose an amount between 10 and
91 Euro (the latter being the expected value of the
lottery).
Let us say, a person states 25 Euro as the according
amount. We want to be able to model the preferences of
this person in the framework of Prospect Theory (PT),
the most commonly used descriptive model for choices
under risk. Can we do this?
It would be natural to answer yes: we just have to
adapt the risk-aversion parameter in the model appro-
priately. In this article, however, we will show that the
answer is no! We cannot model the preference in the
standard framework of PT. The person is too risk-averse
to be described by this theory.
We will generalize this surprising result and prove it in
Section 3.1. Moreover, we will demonstrate that this
effect also causes problems when measuring PT-para-
meters in experiments. In Section 3.2 we see how the
problem can be solved by using an exponential value
function, and in Section 3.3 we study quadratic value
functions. In section 4 we discuss empirical evidence
which confirms the advantages of exponential value
functions. Before that, we start with a short review of PT
(Section 2).
2. Prospect Theory
Prospect Theory (PT) has been introduced by [1] as a
descriptive model for decision making under risk, adding
certain behavioral effects to the classical Expected Uti-
lity Theory:
 Decisions are framed as gains and losses. The utility
function is replaced by a value function v which has
two parts, a concave part in the gain domain and a
convex part in the loss domain, capturing risk-averse
behavior in gains and risk-seeking behavior in losses.
 Probabilities are weighted by an S-shaped probability
weighting function w, overweighting small and un-
derweighting large probabilities.
In this article we will—for simplicity only—consider
two- outcome lotteries in gains, a case where the version
of PT we use in this article coincides with PT’s modern
variant Cumulative Prospect Theory [2].
The value of a lottery with outcomes A and B (
A
<B),
with probability1p

and , is then given by p



  
1,
P
T=w pv A+wpvB (1)
where we denote the probability weighting function by
and the value function by . The value function in
PT is usually chosen as
w v

M. O. RIEGER ET AL. 692
0

, 0
() , 0
xx
vx
xx








(2)
where (the value measured by [2]) is called
the “loss-aversion” coefficient, and describe
the risk-attitudes for gains and losses. It should be
mentioned that coefficients of α, which are fre-
quently used in expected utility theory, cannot be used in
prospect theory, since the function would diverge to
2.25λ
,αβ
0<


at zero and hence could not be extended to negative
outcomes (losses).
The standard weighting function is
 

1
:=
1
γ
γ
γ
γ
p
wp
p+ p
(3)
with the parameter describing the amount of over-
and underweighting.
γ
Although PT as a whole is nowadays the most successful
theory to describe decisions under risk, the specific
choice of the functions and has been criticized for
various reasons:
v w
 First, it is important to keep in mind that a certain
proportion of subjects (around 20%) shows no sign of
probability weighting at all and could be better mo-
deled by expected utility theory [3].
 The standard probability weighting function w be-
comes non-monotone for small values of γ [4,5].1
 The classic value function v leads to non-existence
of equilibria in a financial market of PT-maximizers,
a problem that can be solved by using exponential
value functions [4].
 The interplay of value and weighting functions causes
problems akin to the St. Petersburg Paradox, which
can either be solved by using an exponential value
function or a modified probability weighting function
[5].
 Loss aversion cannot be defined when α
β

[9].
This problem can be solved by using an alternative
value function, e.g. an exponential value function.
In this article we provide more evidence in favor of an
exponential value function instead of the typical power
function (2): we show that the standard choice of a value
function severely limits the amount of risk-aversion that
can be explained with PT (see Proposition 1). As we
have already pointed out, people might show a degree of
risk-aversion that cannot be modeled within the standard
version of PT. This makes it difficult to fit the theory to
some of the experimental data (Section 3.1). The
quadratic utility function, which has played a prominent
role in finance, displays the same limitation (Section 3.3).
We demonstrate that an exponential value function does
not show this problem (Section 3.2). Finally we report
results from a large-scale survey that confirms some
fitting advantage of the exponential value function. May-
be more important is that the survey also demonstrates in
what cases an advantage of an exponential value function
is most visible and—particularly—where not (Section 4).
3. Limits to Risk-Av ersion in Prospect
Theory
3.1. Standard Value Function
Let us neglect for a moment the effects of probability
weighting. Then the parameter


01α, in the defi-
nition of the value function describes the risk-aversion of
a person: a small corresponds to a high risk aversion,
a large is a sign for low risk-aversion, corre-
sponds to risk-neutral behavior.
α
α1α=
If we undertake simultaneous probability weighting,
the interplay between the parameters becomes more in-
volved. Nevertheless, the rule remains so that decreasing
values of will increase the risk-aversion. More
precisely, for a given two-outcome lottery, the certainty
equivalence (CE) of the lottery will decrease, when we
decrease .
α
α
In the following we assume that a person, who decides
about the CE of a two-outcome lottery, will respect
“in-betweenness”, i.e. never choose a CE outside the
interval between A and B.2 When faced with a two-
outcome lottery with positive outcomes A and B (where
A
<B), a person’s CE is therefore bounded from below
by A. However, the CE could a priori be arbitrarily close
to A, if the person is strongly risk-averse.
Is it possible to model such behavior in the standard
form of PT? Surprisingly, the following proposition
gives a negative answer:
Proposition 1. In the standard form of PT, a two-
outcome lottery with positive outcomes A and B (where
A
<B

1wp
) has a CE that is always larger than

wp
A
B
, where p is the probability of the outcome B.
This bound is in particular strictly larger than A.
The proof of this proposition can be found in the
appendix.
Proposition 1 implies that even an extremely risk-
averse person with close to zero can never show a
CE close to A. In fact, the CE of this person must still be
considerably above A. As a numerical example we use
the lottery from the introduction where A = 10, B = 100
and p = 0.9 and assume that (which is
α

0.9 0.5w=
2Cumulative Prospect Theory (and therefore also the form of PT we use
in this article for two-outcome lotteries) satisfies this assumption inde-
p
endently from the choice of the value- and weighting function, thus
we will never get a CE outside the interval (A,B) [14].
1Alternative formulations for w that do not have this problem has been
suggested for CPT, e.g., in [6] and for PT, e.g., in [7] and [8].

M. O. RIEGER ET AL.693
probably a low estimate3). Then
 
132 wp wp
AB=AB
. A person with a CE below 32
is too risk-averse to be described by PT, whatever
“risk-aversion” we choose! Is this surprising im-
plication of the standard PT-model compatible with
experiments?
α
Firstly, we note that many experiments involve only
one positive outcome, i.e. A=0. In this case,
, thus the problem does not arise. There
are, however, also experimental data for
 
10 wp wp
AB

0
A
>. Such
lotteries can already be found in the article of [2].
It is, of course, possible to circumvent the problem by
shifting the reference point to the lower outcome, thus
effectively only considering gambles with A = 0 (with
respect to the reference point). With this trick any
amount of risk-averseness can be explained within the
framework of standard PT for two-outcome lotteries.
There are, however, two major concerns about this ad
hoc method: First, one might complain that this would
not be problem solving, but rather “sweeping the pro-
blem under the carpet” by arbitrarily changing the re-
ference point. Second, the question of what to do if there
is a third outcome arises, e.g. 0, with a very low pro-
bability. Then the trick is not applicable and we are left
in the same situation as before. In short, it is difficult or
impossible to define a consistent rule to choose the re-
ference point that circumvents the problem we have
encountered. Therefore, we decided to refrain from
changing the reference point.
But we still haven’t seen whether the theoretical
bound of risk-averseness is a practical problem. In other
words: are there people who are so risk-averse that their
behavior cannot be explained within the standard for-
mulation of PT?
To check this, we had a look at the lotteries with
0
A
> in the data of [2] and computed the lower bound
for the CE in their model with their parameters (in-
cluding their probability weighting parameter) for all
lotteries with outcomes . Then we compared
the results with the median answer of their respondents.
Moreover, we computed the percentage of respondents
who gave a CE below the theoretical threshold. In other
words: the percentage of participants for each question
who could not be described by the standard form of PT.
(The detailed results are given in the appendix, see Table
1).
0<A<B
For many answers (a total of 28%, but for some
questions up to 48%) the standard form of PT cannot
describe the high levels of risk-aversion measured in this
experiment. Only due to the asymmetry of the weighting
function (i.e.



11wp wp ) the standard form of
PT can at least describe the median level of risk-aversion:
if we omit the probability weighting and take a look at
the cases where (i.e. we assume a symmetric
), we get lower bounds for the CE which are above the
measured median CEs. In other words, asymmetric pro-
bability weighting is in fact needed to “repair” the pro-
blems induced by the value function.
0.5p=
B
w
We summarize this in the following remark:
Remark 1. Proposition 1 is also relevant regarding
probability weighting, since it induces an asymmetric
choice of . The variable assigns smaller weights
to the larger outcome and larger weights to the
smaller outcome
w w
A
, to bring the bound
 
1wp wp
A
B

closer to
A
. In other words, has to be consis-
tently smaller than and hence to be asymmetric.
Given our analysis above, it is not surprising that our
experiments have mostly shown that this asymmetry is in
fact needed, although conceptually, a symmetric function
may be more appealing.

wp
p
The effect shown in the data of Tversky and Kahne-
man, becomes even more visible when we consider lotte-
ries where the probability for the higher outcome is
very large, and at the same time
p
A
is relatively small.
We encountered this problem in data with
undergraduate students, which will be discussed in detail
in the next section. We used two lottery questions of this
type, where we asked for the willingness to pay, and the
majority of students reported a CE below the theoretical
threshold, even for small values of . (The weighting
function becomes non-monotone for too small values of
, hence it is not possible to set smaller than appro-
ximately 0.4.) We report the most important findings
from our preliminary data in the appendix, see Table 2.
5,185N=
γ
γ γ
These results underline once more the gravity of the
problem when measuring PT-values experimentally.
3.2. Exponential Value Functions
Obviously, it would be better to have an index for risk-
aversion that covers the full range of possible risk-averse
behavior, i.e. can be chosen so that in the above two-
outcome lottery every CE larger than
A
can be
reached.
In this section we show that this is possible if we only
change the value function and use -instead of the
standard version- an exponential function, as suggested
by e.g. [4] and [9].
Let us define

1
:=vx e, 0,
e, 0,
x
x
x
x









 (4)
3If we use (3) with γ = 0.4, we obtain w(0.9) ≈ 0.45. This is already
close to the lowest possible value for γ [11], and much smaller than
typical measurements. where


0α,

 and

0β,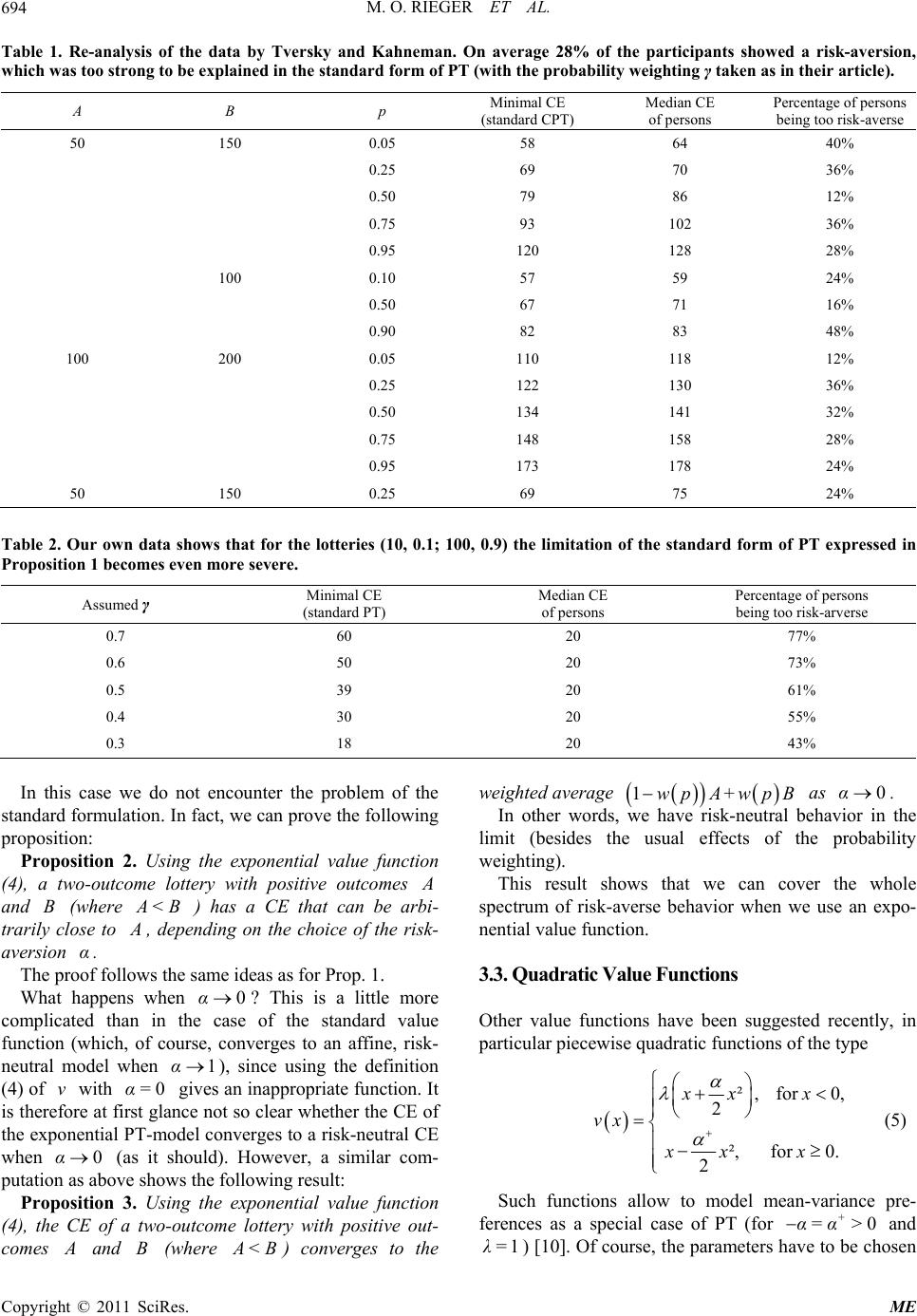

.

M. O. RIEGER ET AL. 694
Table 1. Re-analysis of the data by Tversky and Kahneman. On average 28% of the participants showed a risk-aversion,
which was too strong to be explained in the standard form of PT (with the probability weighting γ taken as in their article).
A B p Minimal CE
(standard CPT)
Median CE
of persons
Percentage of persons
being too risk-averse
50 150 0.05 58 64 40%
0.25 69 70 36%
0.50 79 86 12%
0.75 93 102 36%
0.95 120 128 28%
100 0.10 57 59 24%
0.50 67 71 16%
0.90 82 83 48%
100 200 0.05 110 118 12%
0.25 122 130 36%
0.50 134 141 32%
0.75 148 158 28%
0.95 173 178 24%
50 150 0.25 69 75 24%
Table 2. Our own data shows that for the lotteries (10, 0.1; 100, 0.9) the limitation of the standard form of PT expressed in
Proposition 1 becomes even more severe.
Assumed γ Minimal CE
(standard PT)
Median CE
of persons
Percentage of persons
being too risk-arverse
0.7 60 20 77%
0.6 50 20 73%
0.5 39 20 61%
0.4 30 20 55%
0.3 18 20 43%
In this case we do not encounter the problem of the
standard formulation. In fact, we can prove the following
proposition:
Proposition 2. Using the exponential value function
(4), a two-outcome lottery with positive outcomes
A
and (where B
A
<B ) has a CE that can be arbi-
trarily close to
A
, depending on the choice of the risk-
aversion . α
The proof follows the same ideas as for Prop. 1.
What happens when ? This is a little more
complicated than in the case of the standard value
function (which, of course, converges to an affine, risk-
neutral model when ), since using the definition
(4) of with gives an inappropriate function. It
is therefore at first glance not so clear whether the CE of
the exponential PT-model converges to a risk-neutral CE
when (as it should). However, a similar com-
putation as above shows the following result:
0α
1α
v
α
0α=
0 
Proposition 3. Using the exponential value function
(4), the CE of a two-outcome lottery with positive out-
comes
A
and (where B
A
<B) converges to the
weighted average



 
1wp A+wpB

as . 0α
In other words, we have risk-neutral behavior in the
limit (besides the usual effects of the probability
weighting).
This result shows that we can cover the whole
spectrum of risk-averse behavior when we use an expo-
nential value function.
3.3. Quadratic Value Functions
Other value functions have been suggested recently, in
particular piecewise quadratic functions of the type
², for 0,
0.
+0α>
2
², for
2
xx x
vx
xx x













(5)
Such functions allow to model mean-variance pre-
ferences as a special case of PT (for and
) [10]. Of course, the parameters have to be chosen
α=
1λ=

M. O. RIEGER ET AL.695
so that the highest and lowest outcome of all lotteries are
still in the area where is non-decreasing.4 v
One can now ask whether with such value functions,
arbitrarily strong risk-aversion can be modeled. The an-
swer is again negative. More precisely we have the
following result:
Proposition 4. Using the quadratic value function (5),
the CE of a two-outcome lottery with positive outcomes
A
and (where
B
A
<B
w
) converges to the weighted
average as and to
  
wp pB1A+ +0α

A+ˆ α

BzB as  , where ˆ

is the largest
value of so that is still non-decreasing on
+
αv


0,B .
The proof follows similar ideas as the proofs in the
last section, but this time we use the fact that the
admissible parameter range for is limited for a
given lottery, since otherwise might be decreasing on
the larger outcome of the lottery.
+
α
v
Using the numerical example from the introduction,
we see that the constraint on the admissible risk-
averseness when using a quadratic value function can
even be stronger than in the standard form of PT: for
10
A
=, and we obtain 100B= 0.5z=
ˆ10.0α=B= 1
and
ˆ
36CE

lim


(comparing to
0
lim 32CE
  with the value function (2) of Tversky and
Kahneman).
4. Empirical Evidence
Even though we have seen theoretical arguments for why
the exponential value function should in principle fit
better than the other two functions discussed in Section 3,
only empirical evidence can support our arguments.
There are very few studies comparing the performance of
value functions in PT. Existing empirical evidence still
shows the ambiguity on determining whether the power
function or the exponential function performs better [11].
found that the power function gives better fits whereas
the exponential function performs weakest among the
power, exponential and log quadratic value functions
while using Tversky and Kahneman’s weighting function.
Likewise, the power function and exponential function
were tested as a part of several parametric forms of
cumulative prospect theory (CPT) in [12]. The better fit
of the power function than the exponential function was
pointed out [13]. Fitted CPT using seven deferent value
functions including the three functions mentioned in this
study with seven weighting functions. He also found that
the power value function had better performance than the
exponential function and noticed the weak performance
of the quadratic value function. On the other hand [14],
reported a superior performance of the exponential func-
tion as compared to the power function in CPT using the
standard weighting function.
While the majority of previous studies seem to favor
the power value function, the objective of this section is
to evaluate empirically, which of these specific forms
gives the best explanatory power for new experimental
data and, based on our previous theoretical analysis, to
understand which types of lotteries are better modeled by
a power value function and which by an exponential
value function.
We use data from the international survey on risk atti-
tudes INTRA for our tests [15]. The survey was con-
ducted in 45 countries and regions around the world with
5,912 bachelor students, mostly studying economics,
finance or business. The participants were given ques-
tionnaires that include three time-preference questions,
one ambiguity aversion question, ten lottery questions,
nineteen questions about happiness, personal information,
nationality and cultural origin.
To our knowledge, this is the largest international
survey on risk preferences. Other previous studies have
featured more questions, but relatively few participants.
The advantage of our data is that we can compare the
number of subjects for which a certain model works best.
For the purpose of this study, we concentrate on the
ten lottery questions. See Table 3 for the design of the
lotteries. The survey was translated into local languages.
The monetary payoffs in every question were converted
to the local currency, taking into account each countries’
Purchasing Power Parity and the monthly income/
expenses of local students. The students were informed
before taking the survey that there are no correct or
incorrect answers. There were no monetary incentives
but the survey was conducted in the classroom, leading
to serious participation of most subjects. Pre-tests with
monetary incentives showed no significant difference, as
it is usually the case for lottery questions in gains. We
refer to [15] for further details on the survey.
Among the ten lottery questions were six solely in
gains, one of them had two positive non-zero outcomes.
While most lotteries were on amounts of around $100,
there was one large-stake lottery (winning $10,000 with
prob. 60%).
The first measured parameter was the amount of risk
averseness in gains, estimated from the six lotteries with
outcomes only in gains.
The second measured parameter (the amount of risk
seeking in losses) was estimated from the two lotteries
with results in the loss region. The students were
instructed to imagine that they had to play these lotteries,
unless they paid a certain amount of money beforehand.
This amount of money is the negative value of willing-
ness to pay or so called willingness to accept. These are
4Alternatively, one can “cut” the function outside this area so that it
simply becomes constant for large values.

M. O. RIEGER ET AL. 696
Table 3. Design for the ten lotteries in INTRA.
Lottery Outcome A($) Prob(A) Outcome B($) Prob(B) Average Value($)
1* 10 0.1 100 0.9 91
2 0 0.4 100 0.6 60
3 0 0.1 100 0.9 90
4** 0 0.4 10,000 0.6 6000
5 0 0.9 100 0.1 10
6 0 0.4 400 0.6 240
7 –80 0.6 0 0.4 –48
8 –100 0.6 0 0.4 –60
9 –25 0.5 - 0.5 -
10 –100 0.5 - 0.5 -
*type A-lottery (two positive outcomes); **type B-lottery (large stake).
lottery 6 and lottery 7 in Table 3.
The third measured parameter was the loss-aversion
parameter, based on the two last lotteries by the
following question:
In the following lotteries you have a 50% chance to
win or lose money. The potential loss is given. Please
state the minimum amount $X for which you would be
willing to accept the lottery.
We excluded those individuals who had not completed
all the lotteries, leaving 5,185 subjects for our analysis.
We used the grid search method to estimate all the
parameters for the weighting function and value
functions by minimizing the sum of normalized errors,
where the parameter values of α,
β
varied from 0 to 1
for the standard value function, from 0 to 0.1 for the
exponential function and from 0 to .005 for the quadratic
value function5, and varied from 0 to 1. Parameters
were predicted on an individual level to each of three
models to access the functional performance individually.
The error function was defined as the sum of the absolute
differences between the CE and the maximum outcomes
of the lotteries. The normalized errors are the proportion
of those differences and the lottery’s maximum outcome
for each lottery.
γ
To study the specific effect of lotteries with two
positive outcomes (type A) and of large-stake lotteries
(type B), we computed the best fitting models for three
scenarios: No lotteries of type A and B. / No lottery of
type B. / All lotteries.
According to our theoretical results, type A lotteries
should favor exponential value functions as might type B
lotteries. The results are shown in Figure 1.
We can see that when removing the type A lottery
(with two positive outcomes) and the type B lottery (with
large outcome) the power value function works better
than the exponential function. However, the exponential
value function outperforms the power value function
when plugging in the lottery with two positive outcomes,
or both the lottery with two positive outcomes and the
lottery with the large outcome.
A paired t-test of the average ranks to collate the
performance of power and exponential value functions is
highly significant at


5184 11.13t= with 6,
which shows that in this case the exponential function is
better. The frequency, in which the quadratic value
function works best, is very low (about 1%).
0.0001p<
The important lesson to learn from this result is that
the optimal choice of the value function strongly depends
on the lotteries in the experiment!
5. Conclusions
We have seen that the standard form of PT faces severe
problems when people show strong risk-aversion, since
the smallest possible CE according to this theory is still
substantially above the lowest lottery outcome, when
considering lotteries with two positive outcomes. This
makes it impossible to describe very risk-averse behavior
correctly. Experimental data shows that such degree of
risk-aversion is quite frequent and not a marginal pheno-
menon. The problem is mitigated by the asymmetry of
the weighting function and one can conjecture that it is
the main reason for why this asymmetry is needed. The
difficulties disappear completely when replacing the
standard power value function by an exponential func-
tion. This description allows to cover all degrees of risk-
aversion which do not violate “in-betweenness”. Another
advantage of experimental value functions can be found
for large-stake gambles, as our empirical results show.
As in many experiments, both types of lotteries (with
5The value has to be bounded from below to avoid non-monotonic
value functions on the relevant range of outcomes.
6All models are ranked individually using the errors calculated as ex-
p
lanatory performance 1 as best performance, 3 as worst performance.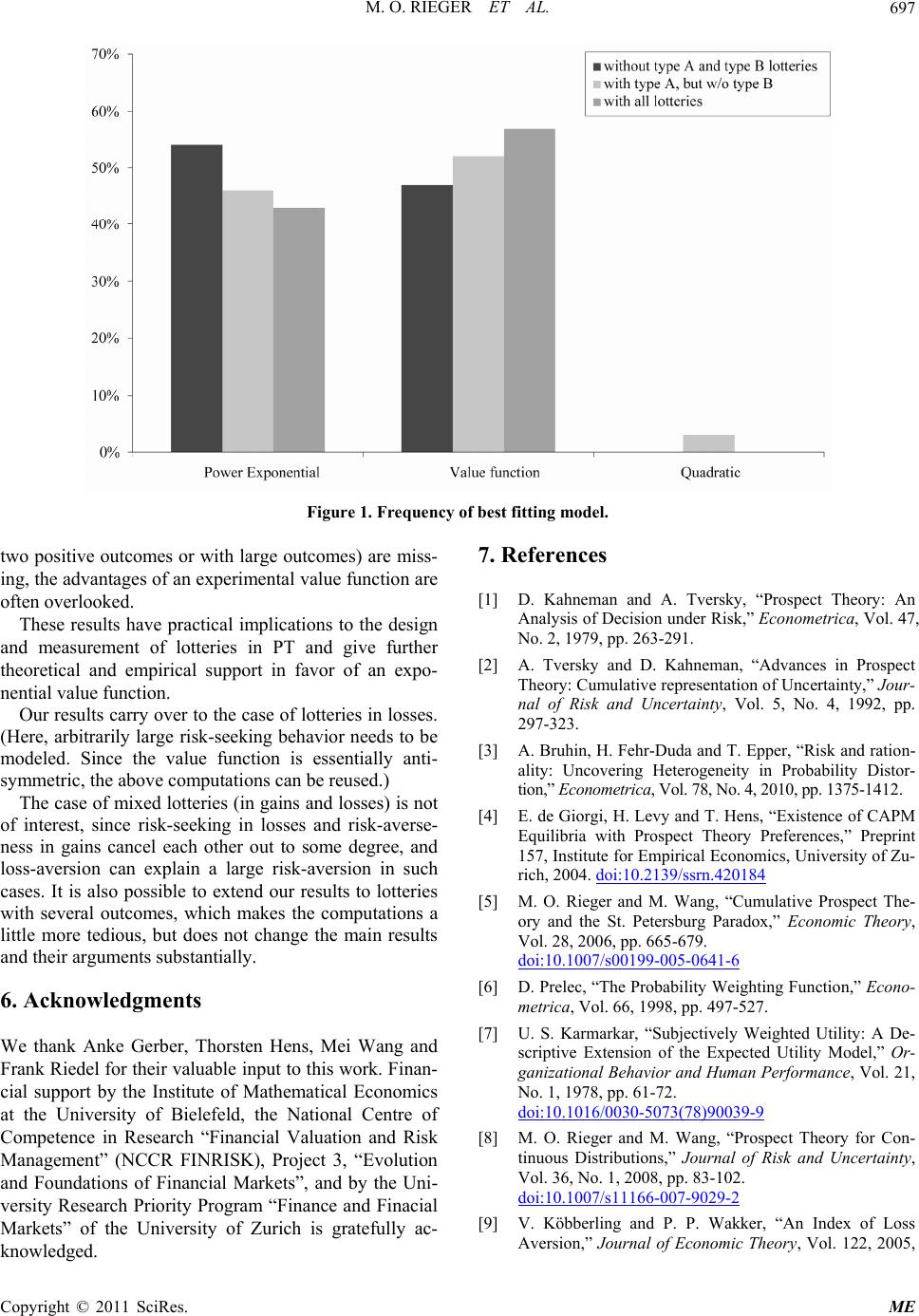

M. O. RIEGER ET AL. 697
Figure 1. Frequency of best fitting mode l.
two positive outcomes or with large outcomes) are miss-
ing, the advantages of an experimental value function are
often overlooked.
These results have practical implications to the design
and measurement of lotteries in PT and give further
theoretical and empirical support in favor of an expo-
nential value function.
Our results carry over to the case of lotteries in losses.
(Here, arbitrarily large risk-seeking behavior needs to be
modeled. Since the value function is essentially anti-
symmetric, the above computations can be reused.)
The case of mixed lotteries (in gains and losses) is not
of interest, since risk-seeking in losses and risk-averse-
ness in gains cancel each other out to some degree, and
loss-aversion can explain a large risk-aversion in such
cases. It is also possible to extend our results to lotteries
with several outcomes, which makes the computations a
little more tedious, but does not change the main results
and their arguments substantially.
6. Acknowledgments
We thank Anke Gerber, Thorsten Hens, Mei Wang and
Frank Riedel for their valuable input to this work. Finan-
cial support by the Institute of Mathematical Economics
at the University of Bielefeld, the National Centre of
Competence in Research “Financial Valuation and Risk
Management” (NCCR FINRISK), Project 3, “Evolution
and Foundations of Financial Markets”, and by the Uni-
versity Research Priority Program “Finance and Finacial
Markets” of the University of Zurich is gratefully ac-
knowledged.
7. References
[1] D. Kahneman and A. Tversky, “Prospect Theory: An
Analysis of Decision under Risk,” Econometrica, Vol. 47,
No. 2, 1979, pp. 263-291.
[2] A. Tversky and D. Kahneman, “Advances in Prospect
Theory: Cumulative representation of Uncertainty,” Jour-
nal of Risk and Uncertainty, Vol. 5, No. 4, 1992, pp.
297-323.
[3] A. Bruhin, H. Fehr-Duda and T. Epper, “Risk and ration-
ality: Uncovering Heterogeneity in Probability Distor-
tion,” Econometrica, Vol. 78, No. 4, 2010, pp. 1375-1412.
[4] E. de Giorgi, H. Levy and T. Hens, “Existence of CAPM
Equilibria with Prospect Theory Preferences,” Preprint
157, Institute for Empirical Economics, University of Zu-
rich, 2004. doi:10.2139/ssrn.420184
[5] M. O. Rieger and M. Wang, “Cumulative Prospect The-
ory and the St. Petersburg Paradox,” Economic Theory,
Vol. 28, 2006, pp. 665-679.
doi:10.1007/s00199-005-0641-6
[6] D. Prelec, “The Probability Weighting Function,” Econo-
metrica, Vol. 66, 1998, pp. 497-527.
[7] U. S. Karmarkar, “Subjectively Weighted Utility: A De-
scriptive Extension of the Expected Utility Model,” Or-
ganizational Behavior and Human Performance, Vol. 21,
No. 1, 1978, pp. 61-72.
doi:10.1016/0030-5073(78)90039-9
[8] M. O. Rieger and M. Wang, “Prospect Theory for Con-
tinuous Distributions,” Journal of Risk and Uncertainty,
Vol. 36, No. 1, 2008, pp. 83-102.
doi:10.1007/s11166-007-9029-2
[9] V. Köbberling and P. P. Wakker, “An Index of Loss
Aversion,” Journal of Economic Theory, Vol. 122, 2005,

M. O. RIEGER ET AL. 698
pp. 119-131.
[10] V. Zakalmouline and S. Koekebakker, “A Generalization
of the Mean-Variance Analysis,” SSRN Working Paper,
2008.
[11] C. Camerer and T.-H. Ho, “Violations of the betweenness
Axiom and Nonlinearity in Probability,” Journal of Risk
and Uncertainty, Vol. 8, No. 2, 1994, pp. 167-196.
[12] M. Birnbaum and A. Chavez, “Tests of Theories of Deci-
sion Making: Violations of Branch Independence and
Distribution Independence,” Organizational Behavior
and Human Decision Processes, Vol. 71, No. 2, 1997,
pp. 161-194.
[13] H. Stott, “Cumulative Prospect Theory’S Functional Me-
nagerie,” Journal of Risk and Uncertainty, Vol. 32, No. 2,
2006, pp. 101-130. doi:10.1007/s11166-006-8289-6
[14] S. Blondel, “Testing Theories of Choice under Risk: Es-
timation of Individual Functionals,” Journal of Risk and
Uncertainty, Vol. 24, No. 3, 2002, pp. 251-265.
doi:10.1023/A:1015687502895
[15] M. Wang, M. O. Rieger and T. Hens, “Prospect Theory
around the World,” SSRN Working Paper, 2011.
[16] A. Mas-Colell, M. D. Whinston and J. R. Green, “Micro-
economic Theory,” Oxford University Press, Oxford,
1995.

M. O. RIEGER ET AL.699
Appendix
Proof of Proposition 1
Let the probability for the outcome be given by
and denote . Then the CE of the lottery is in
general given by
B p

:=zwp




11CE=vzvA+ zvB 

,
where denotes the inverse map of , i.e.
.
1
v
 
x
v

1
vv =x

In the standard form of PT, this becomes


1
1a
αα
CE =zA+ zB.
Although conceptually unrelated, this expression is
mathematically equivalent to the CES (constant elasticity
of substitution) utility function of two goods as given by


1
1211 22
ρ
ρρ
ux,x =αx+αx (with constants , 2).
The limit of the CES utility preferences for is
the preference described by the Cobb-Douglas utility
function
1
α
ρ
α
0

12
12
uxxx


 [16, page97]. This result
implies Proposition 1. Alternatively, a direct proof can
be given by computing the limit of the certainty
equivalent for via a Taylor expansion. □ 0α
Proof of Proposition 2
To prove this result, we first note that the new risk-
aversion parameter α scales differently than before:
high risk-aversion corresponds to a large value of ,
low risk-aversion corresponds to an close to zero. In
fact, the CE decreases monotonically in which we
can prove as follows: compute the CE of the lottery, set,
as before,
α
α
α


:=zwp
α
, multiply (for computational con-
venience) by and take the derivative with respect to
to obtain α








dd
ln 1ee
dd
1e e
1
=ln1ee1e e)
AB
AB
AB
AB
CEz z
Az Bz
zz zz












 
 .
Using the strict concavity of the logarithm and bring-
ing both resulting terms on the some denominator, we
arrive at
 









2222
2
eeeee
d.
d1e e1e e
αAαBαBαAαAαB
αAαBαAαB
Azz+Bz zAzzBz zAB
CEz z
z+z z+z

 
 
  
 

e


Since and , this expression is
negative, and thus the CE is monotonically decreasing in
. We compute its limit as using the refor-
mulation

01z,B>A
αα 












 
1ln 1ee
1
lne1e
1
lneln1e
1
=ln1e1.
αAαB
αBA
αA
αBA αA
αBA
CEz+ z
α
z+z
α
+z+z
α
A+z
α



 


 
 

Since and
0α>
A
<B
1z<
, we have ,
and therefore we obtain the following two inequalities,
where we recall that and thus ln :


e0
αBA , 


1z>
1




ln 1ln 1e10.
αBA
z< +z<


Inserting these inequalities into (6), we obtain bounds
for the CE, namely:

1ln 1.
A
<CE<A z
α

As , the right hand side converges to α
A
, and
thus and Proposition 2 is proved. □
limCE =A
 
Proof of Proposition 3
We start from the CE and frstly expand the exponential
function and then the logarithm:



 





 
2
2
1ln1
1ln 11
11
1.
αAαB
CEze+ ze
α
=+zAzBα+O α
α
zA zBα+Oα
α
=zA+zB+Oα



 

The limit concludes the proof of Proposition
3. □
0α
Original Survey Questions
The lottery questions in the INTRA survey were formu-
lated as follows:
Imagine you are offered the Lotteries below. Please
indicate the maximum amount you are willing to pay for
the lottery.

M. O. RIEGER ET AL. 700
Lottery 1
10% chance Win 4 £
90% chance Win 40 £
I am willing to pay at most £____ to play the lottery.
The lotteries themselves can be found in Table 3.