ABSTRACT

Hereby it studied the fundamental theory created by the London brothers for interpretation of the magnetic field reduction in superconductors. As demonstrated, this theory is not correct. The author of this work has developed the new theory of superconductivity. The equation describing the electron distribution function under the effect of magnetic field explains existence of the Meissner-Ochsenfeld effect. It is shown that the critical field equation matches the width of a potential well in the kinetic energy dependence of mean electron energy. As a result, the supercurrent density formula has been derived. Existence of magnetic fields is explained by two steady-state Maxwell equations. There are magnetic fields that are found to be created in individually shaped metals. Penetration of the external magnetic field in a superconductor has been explained.

Subject Areas:

Theoretical Physics

Keywords:

Electron Distribution Function, Anisotropy, Superconductivity, Energy Gap, Magnetic Field in Superconductor

1. Introduction

Kamerlingh Onnes discovered the phenomenon of superconductivity at Leiden Laboratory, Holland, in 1991 [1] . While investigating temperature dependence of Hg resistance, he could find that when the material is cooled down to about 4 K temperature the resistance drops abruptly to zero. The very phenomenon was called superconductivity. Shortly thereafter, other elements exhibiting similar properties were discovered. The superconductor resistance measurement pattern is demonstrated in Figure 1.

A superconductor is immersed in liquid helium. Initially, weak current is supplied from a battery. Then, temperature is reduced. When temperature falls below the defined value, the superconductor circuit is shorted. The superconductor circuit current sustains its steady state as long as it can. A magnetic needle provided as a detector finds some persistent current in the superconductor, thus indicating to the magnetic field produced in the solenoid. The pattern of temperature T dependence of specific resistance ρ in a superconductor is shown in Figure 2. Temperature T_c is named for critical temperature. This means that we cannot measure resistance of the superconductor. The matter is that the superconductor has the property that makes impossible to measure any specific resistance.

Shortly thereafter, it was discovered that such superconductivity disappears when a test piece is placed in a relatively weak magnetic field. This phenomenon was discovered by Meissner and Ochsenfeld [2] . Value H_m of the magnetic field strength in which superconductivity is disrupted is called a critical field. The temperature dependence of the critical field is described by the following empirical formula:

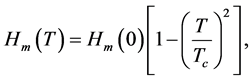(1.1)

where 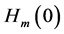is a critical field produced at absolute zero of temperature T = 0. Dependence (1.1) is shown in Figure 3. Plane (H, T) represents a phase diagram of the superconductive state. Substance in the superconductive state S is shown below the curve (1.1) and this substance in the normal state N?above the curve. The superconductor that demonstrates such states is named for the type-I superconductor.

Brothers Fritz and Heinz London developed the first macroscopic theory of superconductivity in 1935 [3] . They mathematically formulated the theory based on principal experimental factors:

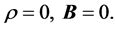(1.2)

Here B is magnetic induction inside a superconductor. Such facts have been accepted a priori. But why does the specific resistance go to zero? There might be other superconducting factors that make it impossible to measure ρ. Why does it occur that the magnetic induction inside a superconductor gets equal to zero? The facts accepted a priori should be proved.

Let’s take B for magnetic induction of the external field. The London brothers have derived the following external magnetic field equation:

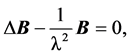(1.3)

where

(1.4)

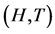Value 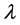is called London length of the magnetic field to be penetrated in a superconductor.

Let us assume the superconductor occupies half-space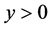, and region 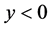is filled with the vacuum where magnetic field B_o runs along the interfacial area (see Figure 4). In this case, the Equation (1.3) is formulated as:

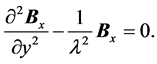(1.5)

The solution of the Equation (1.5) is formulated as follows:

(1.6)

It should be noted that this function does not agree with the Meissner-Ochsenfeld effect. When magnetic field strength at the surface of the conductor exceeds critical value 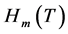the superconductivity disappears. But the function (1.6) does not depend on the critical field at all. In addition to, the superconductivity is taken for the equilibrium state of a substance?i.e. all values are not to depend on time t. But all these dependences are derived in the London brothers’ equation. The supercurrent can flow over the entire surface of the superconductor. This current can create self-magnetic field 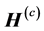in the substance. The London brother’s theory does not take into consideration such self-magnetic field.

There are two magnetic fields in the superconductor. One magnetic field is created by the supercurrent and another external field is induced from other sources. The compass needle shown in Figure 1 responds to the supercurrent-induced field. Let’s denote such strength of field by parameter 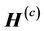and name this field for the super conductor self-generated magnetic field. We shall denote strength of other magnetic fields by parameter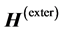. This is an external magnetic field. Let the strength of the external magnetic field on the surface of the superconductor is equal to. The Meissner-Ochsenfeld effect may be expressed by the following inequality. Superconductivity is generated in metal when its temperature T drops down below the critical temperature T_c:

(1.7)

wherein the strength of the external magnetic field at the surface of the superconductor is less than that of the critical field:

(1.8)

In other cases the superconductor will represent ordinary metal properties.

2. New Theory of Superconductivity

The new density-matrix based superconductivity theory has been developed and described in the works [4] - [12] . The formula that explains two electron metal interaction energy ε_kk' with wave vectors k and k’ has been derived in the work [6] .

(2.1)

where I and J are energy dimension constants, is a Kronecker symbol. Value I specifies the electron repulsion energy with wave vectors k and −k and value J is the electron attraction energy with equal wave vectors. Using the variational principle it is possible to derive the equation for the wave vector electron distribution function w_k:

(2.2)

where function satisfies the normalizing condition

(2.3)

Here G is a number of valence states specified in one crystal lattice point, N is a number of electrons within the lattice.

The equations (2.2) may be easily solved by means of a computational modeling method. At temperatures, the kinetic energy ε dependence of function is specified as the single-valued one. But when the plot of function to be specified within a certain range of values of kinetic energy ε is represented by the multi-valued function. Consequently, the critical temperature value will be expressed as follows:

(2.4)

The plot of the distribution function w(ε, τ) that complies with temperature T = 0 and parameters is demonstrated in Figure 5. Wherein:

(2.5)

Let us denote the values of multiple-valued function by two single-valued functions, in particular, and These functions can be expressed as:

There can be the anisotropic solution made when functions and are unequal. At higher temperatures the anisotropic solution is decreased and thereafter disappears when the temperature goes to the critical value. The superconductive state of metal can be obtained by means of the anisotropic electron distribution function.

Actually, electrons exhibit their lowest energy macro-state. At T = 0, the energy will be minimized to the state expressed by the following formula:

(2.6)

This function obtains anisotropy at. This function is graphically demon-strated in Figure 6.

The mean electron energy is:

. (2.7)

The kinetic energy ε dependence of the mean electron energy can be expressed by the following formulas:

(2.8)

(2.9)

Here, is an electron kinetic energy interval with the anisotropic distribution function. The function produced beyond the above interval is isotropic and brought to. This dependence is graphically demonstrated in Figure 7 for various temperatures τ.

The plots demonstrated have the following specific features. At temperature a “well” is formed at each curve of dependence that meets the values of kinetic energy satisfying the following inequalities:

(2.10)

Value is the least one of electron kinetic energy ε applicable for determination of functions and. Value satisfies the condition that is shown below:

(2.11)

according to which the “well” edges graphically specified by dependence are positioned at the same level. Some kind of an opening occurs at the right-hand edge of

the function. This means that there is a “gap” in the range of values of the electron energy. Gap width ∆ grows up from zero to J value while temperature is reduced from T_c to zero. The well width

(2.12)

also grows up from zero to I value while temperature is decreased down to T = 0.

3. Superconductor-Derived Magnetic Field

Let us assume that a superconductor is in the magnetic field which strength will be denoted by the H value. The electron energy values have been found in the works [9] [11] [12] , in particular:

(3.1)

where

(3.2)

(3.3)

is a Bohr magneton, is a spin wave function.

On minimizing thermodynamic potential Ω with account for the energy values (3.1), we can obtain the nonlinear equation to be applied for determining wave vector electron distribution function within the magnetic field:

(3.4)

If

(3.5)

than the Equation (3.4) will have the previous solution:

(3.6)

Let’s assume that. As provided by the Equation (3.5), we shall obtain the expression. This means that the plot of the electron wave vector distribution function is shifted to the right by value Λ as compared with that when no magnetic field isapplied.

It is necessary to find the lowest electron energy (3.1) for obtaining the real-valued distribution function. Now, let us study the case when a magnetic field destroys superconductivity at T = 0.

Let

. (3.7)

The lowest energy (3.1) may be found when function w_k is expressed as follows:

(3.8)

As it is shown above, function w_k is to be isotropic?i.e. the superconductive state disappears. The distribution function plot is shifted to the right by value I while the magnetic field destroys the superconductive state that consequently disappears (see Figure 8).

4. Meissner-Ochsenfeld Effect

Let’s assumed that value Λ is equal to I. In this case, the distribution function is shifted to the right. We shall find the critical magnetic field strength at T = 0 using the Formulas (3.2) and (3.7).

(4.1)

If the temperature grows up above zero, the critical magnetic field strength, according to the Formula (3.2), will be represented by the expression:

(4.2)

where is the width of the potential well (2.12) in the kinetic energy dependence of the mean electron energy. Using the above formulas we can obtain the relation:

(4.3)

The relation is approximately equal to 1:

Now, we shall compare the plot of the critical field (see Figure 3) with the theoretical points set out on the curve of the kinetic energy dependence of the mean electron energy (see Figure 7). The matching point pattern is shown in Figure 9.

5. Supercurrent

If no magnetic field is applied, the width of the well is to be equal to. With the magnetic field of H strength applied to the surface of the superconductor, the electron distribution function is shifted to the right by value Λ. In this case, the pattern of the energy well remains unchanged but it is shifted to the right. Let us assume that according to (3.2) the electron energy will accept the least value while a portion of the well is shifted by the value obtained from the expression. Consequently, the superconducting width of the well will be:

(5.1)

We shall now substitute value of the Equation (5.1) using the Formula (4.2). As a result, we are to obtain:

(5.2)

When strength H of the magnetic field gets its critical value, the superconducting with of the well will be brought to zero.

Now, we shall use the formula derived in the works [11] [12] for the current density in superconductors:

(5.3)

where, is the energy Fermy. When the magnetic field strength exceeds its critical value, superconductivity disappears and thereafter the substance conductivity only may be applied for determination of the current density vector.

6. Magnetic Field within the Planar Structure

Basically, equilibrium values of the magnetic field may be obtained from steady state Maxwell’s equations:

(6.1)

(6.2)

For finding the solution to this problem, it is necessary to know the current density.

Let us study the magnetic field applied to the planar surface of the superconductor when the H-vector induces the effect acting paralleled to this surface. The x axis is placed along the conductor and parallel to the H-vector, the y axis is arranged perpendicularly to the surface and the z axis faces us (see Figure 10).

In this case, the Equation (6.1) is expressed as follows:

(6.3)

Since the supercurrent is created by a negative component of vector, with the equation value (5.3) substituted we shall obtain:

(6.4)

where

(6.5)

The superposition principle-based H-vector is equal to the sum of the external field and magnetic field as being induced by supercurrent flows:

(6.6)

The projection of the complete field will be represented by the following expression:

(6.7)

With the above equation substituted into the Formula (6.4), the following expression is formulated:

(6.8)

Let’s assume that any supercurrent to be produced in a substance is flowing along the z axis and the external magnetic field is not applied:

Such current may flow along the surface of the superconductor for an unlimited duration. The supercurrent creates the self-magnetic field that will satisfy the equation:

(6.9)

The supercurrent-induced field strength applied to the superconductor surface will be equal to zero:

(6.10)

The strength that satisfies such condition will be expressed by the formula:

(6.11)

The plot of this function is demonstrated in Figure 11.

Now, we shall create the x-directed external magnetic field with its strength denoted by the parameter. This function will satisfy the equation derived from the expression (6.8):

(6.12)

Let us assume that the magnetic field satisfies the original condition:

(6.13)

The solution of this equation will be formulated as follows:

(6.14)

Hence, we have obtained some kind of decay of the superconductor inwardly directed external magnetic field strength. But the character of decay does not match the function predicted by the London equation:

(6.15)

The plot of the function (6.14) is shown in Figure 12.

The complete field (6.7) will take up the following form:

(6.16)

Now, we shall find the supercurrent density by the Formula (5.3) as a function of the y coordinate. For this purpose, we shall substitute the Formula (6.16) into the Equation (5.3). As a result, we shall obtain:

(6.17)

where

(6.18)

As it is seen from the above formula, the current density exponentially decays in the direction off the superconductor surface. When the strength of the external field goes to that of the critical field, the strength of the complete field (6.16) will be expressed by equation. In this case, the supercurrent density (6.17) will be equal to zero and the superconductivity disappears.

Let us study the case when the external field strength is applied in the opposite direction:

(6.19)

This will result in failed application the Meissner-Ochsenfeld effect. For correcting such condition it should be noted that the external field actually changes direction of supercurrent flow. Hence, it should be noted that the direction of the superconductor self-magnetic field H-vector matches that of the external magnetic field strength. As

provided by the above calculations, the external magnetic field decays inside a conductor when being exposed to the supercurrent-induced magnetic field.

We have discussed the absolutely correct solutions of the Maxwell’s and current density equations in this Section. Some approximate expressions for supercurrent and magnetic fields will be discussed below.

7. Penetration of Magnetic Field in Flat Disc of Superconductor

Let the superconductor be a flat disk. An external magnetic field is perpendicular to the plane of the disk (see Figure 13). Self-magnetic field will be directed in the same direction as the external field. If the temperature is less than critical:, then the metal will be superconductive. But this external field strength should be less than the critical field:.

The superconducting current density will flow over the disk surface (see Figure 14). We write the approximate expression for the unit j of the superconducting current density by analogy with Formula (6.17):

(7.1)

where r is the radial coordinate, R is the radius of the superconducting disk. The moduli of tension of self-magnetic field produced by superconducting current and the external magnetic field inside the drive will be approximately equal, if these formulas are constructed like Formulas (6.11) and (6.14):

(7.2)

(7.3)

If you turn off the external magnetic field, a superconducting current will flow through the disk, the magnitude of which is equal to

(7.4)

and the magnitude of the tension of the self-magnetic field remains the same. Figure 15 shows field lines.

8. Magnetic Field inside a Superconducting Sphere

Let’s discuss the behavior of the H magnetic field inside and outside a spherically shaped superconductor. The conductor with no superconducting properties induced at temperature is shown in Figure 16. External magnetic field penetrates inwards the conductor in such a ways as described by the solution of the Maxwell equation.

When temperature drops down below the critical value: superconductive function is induced in the conductor. This is the condition when the magnetic field is forced out of the conductor. This condition is demonstrated in Figure 17. Such pattern is produced under the Meissner-Ochsenfeld effect and exists until the strength of the external field modulus applicable to the superconductor surface remains less than that

of the critical field:. Should the external field strength go to its critical value, the superconductivity disappears and the function is brought to the pattern shown in Figure 16.

Let’s implement spherical coordinates and inside the sphere where is a distance from the sphere center to any arbitrary point of a space; is a longitude angle. The modulus of vector to be produced by superconductive current is equal to:

(8.1)

where R is a sphere radius. For the purpose of current density, conditions and

are to be followed to apply the superconductive function. As soon as or, the current density (8.1) goes down to zero and the superconductive function disappears. Supercurrent flows along the spherical surface (see Figure 17).

External magnetic field is not capable to penetrate deep inwards the superconductor and its modulus is equal to

(8.2)

The above formula demonstrates the influence of the external field on the supercurrent density. As soon as, the current density (8.1) goes down to zero. As a result, the superconductive function disappears. Now, we can use magnetic field induced by the supercurrent inside the conductor. Its modulus is equal to:

(8.3)

These fields are shown in Figure 17.

Now, we switch off the external magnetic field. In this case, its modulus applicable to the conductor surface is to be equal to zero. When temperature goes down below the critical value, the superconductive function does not disappear. The supercurrent being expressed by the following equation

(8.4)

will be much the same as before. The pattern of self-magnetic field lines only will obtain a few changes (see Figure 18).

9. Supercurrent Flowing through a Coil

Let us discuss about a superconducting wire coil. Current flows through such conductor passing each circular loop. Much the same current flows over a thin-coat disk surface (see Figure 15). For making a circular coil a core of the disk may be cut out (see Figure 19). Both the self-magnetic field (7.2) and current density (7.4) shall save their characteristics:

(9.1)

and coil plain:

(9.2)

10. Supercurrent Flowing through a Solenoid

Now, let’s discuss about a superconducting solenoid. Current may flow passing through a circular loop similar to that described in the previous section. But the solenoid will have exceeded self-magnetic field. If there are N coils in the solenoid, then the strength of the magnetic field within its core will go to―i.e. the strength will grow up proportionally (see Figure 20).

11. Conclusions

Hence, we can explain the cause of behavior by reference to external magnetic field that is forced out of a superconductor. In case of absence of any superconductivity, external magnetic field in metal passes through the material. With superconductivity being induced in metal (i.e. newly generated supercurrent in material), current flowing along the surface is featured with its specific density. Currents flow over closed curves and create self-magnetic field. Self-magnetic field is added to external magnetic field due to the superposition principle.

If to compare moduli of such fields, we can seen that the external magnetic field modulus is characterized by H_o and self-magnetic field?by. According to the Meissner-Ochsenfeld effect, superconductivity can exist when. This is the reason why an external magnetic field is forced out of a superconductor. External magnetic field is forced out under the effect of self-magnetic field due to supercurrent that exists in the material.

Cite this paper

Bondarev, B.V. (2016) New Theory of Superconductivity. Does the London Equation Have the Proper Solution? No, It Does Not. Self-Generated and External Magnetic Fields in Super- conductors. Open Access Library Journal, 3: e3148. http://dx.doi.org/10.4236/oalib.1103148

References