ABSTRACT

An identification problem is considered as inaccurate measurements of dynamics on a time interval are given. The model has the form of ordinary differential equations which are linear with respect to unknown parameters. A new approach is presented to solve the identification problem in the framework of the optimal control theory. A numerical algorithm based on the dynamic programming method is suggested to identify the unknown parameters. Results of simulations are exposed.

Keywords:

Nonlinear System, Optimal Control, Identification, Discrepancy, Dynamic Programming

1. Introduction

Mathematical models described by ordinary differential equations are considered. The equations are linear with respect to unknown constant parameters. Inaccurate measurements of the basic trajectory of the model are given with known restrictions on admissible small errors.

The history of study of identification problems is rich and wide. See, for example, [1] [2]. Nevertheless, the problems stay to be actual.

In the paper a new approach is suggested to solve them. The identification problems are reduced to auxiliary optimal control problems where unknown parameters take the place of controls. The integral discrepancy cost functionals with a small regularization parameter are implemented. It is obtained that applications of dynamic programming to the optimal control problems provide approximations of the solution of the identification problem.

See [3] [4] to compare different close approaches to the considered problems.

2. Statement

We consider a mathematical model of the form

(1)

where 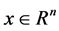is the state vector, , 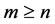is the vector of unknown para- meters satisfying the restrictions

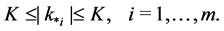(2)

Let the symbol 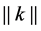denote the Euclidean norm of the vector.

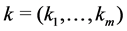It is assumed that a measurement of a realized (basic) solution of Equation (1) is known, and

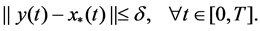(3)

We consider the problem assuming that the elements 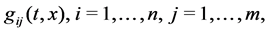of the matrix 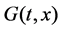are twice continuously differentiable functions in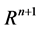. The coordinates 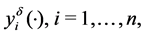of the measurement 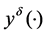are twice continuously differentiable functions in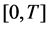, too. The coordinates of the vector- function are continuous functions on the interval.

We assume also that the following conditions are satisfied

There exists such constants and that for all the inequalities

(4)

are true.

There exist such constant (from) and such compact set that for any the following conditions are held

;

.

Here.

The identification problem is to create parameters such, that

(5)

where is the solution of Equation (1), as

3. Solution

3.1. An Auxiliary Optimal Control Problem

Let us introduce the following auxiliarly optimal control problem for the system

(6)

where is a control papameter satisfying the restrictions

(7)

for a large constant.

Admissible controls are all measurable functions. For any initial state, the goal of the optimal control problem is to reach the state and minimize the integtal discrepancy cost functional

(8)

Here is the given measurment; is a small regularization parameter, is the trajectoty of the system (6), (7) generated under an admissible control out the initial point. The sign minus in the integrand allows to get solutions which are stable to perturbations of the input data.

N o t e 1. A solution of the optimal control problem (6), (7), (8) allows us to construct the averaging value

(9)

which can be considered as an approximstion of the solution of the identification problem (1), (2).

3.2. Necessary Optimality Conditions: The Hamiltonian

Recall necessary optimality conditions to problem (6), (7), (8) in terms of the hami- ltonian system [5] [6].

It is known that the Hamiltonian to problem (6), (7), (8) has the form

where is an ajoint variable, the symbol denotes the transpose operation.

It is not difficult to get

where

Here the vector-column has the form

(10)

3.3. The Hamiltonian System

Necessary optimality conditions can be expressed in the hamiltonian form. An optimal trajectory generating by an optimal admissible control in problem (6), (7), (8) have to satisfy the hamiltonian system of differential inclusions

(11)

and the boundary conditions

(12)

where symbols denote Clarke’s subdifferentials [7] and,.

Parameters belong to the intervals where values and are choosen from the conditions

(13)

We introduce the last important assumption.

There exists a constant such that restrictions on controls in problem (6), (7), (8) satisfy the relations

(14)

where are from (10).

N o t e 2. Using definition (10) one can check that constant K, satisfying assumtion, can be taken as

,

where

Here are components of matrix and are components of matrix.

If and the Hamiltonian has the simple form

and the differential inclusions (11) transform into the ODEs.

(15)

Let us introduce the discrepancies, and obtain from (15) the following equations

(16)

and the boundary conditions

(17)

where saisfy (13).

3.4. Main Result: Dynamic Programming

Using skims of proof for similar results in papers [8] [9] [10] we have provided the following assertion.

Theorem 1 Let assumptions be satisfied and the concordance of para- meters: takes place, then solutions of problem (11), (12), (13) are extendable and unique on for any saisfying (13) and

(18)

It follows from theorem 1, that the average values (9) obtained with the help of dynamic programmig satisfy the desired relation

(19)

4. Numerical Example

A series of numerical experiments, realizing suggested method, has been carried out. As an example a simple mechanical model has been taken into consideration.

This simplified model describes a vertical rocket launch after engines depletion. The dynamics are described as

(20)

where is a vertical coordinate of the rocket, is an unknown windage coefficient and =9.8 is a free fall acceleration.

A function is known and satisfies assumption. This function was obtained by random perturbing of the basic solution for =0.3.

The suggested method is applied to solve the identification problem for = 0.3.

We introduce new variables and transform Equation (20) into

(21)

where and is a fictitious control, which was introduced in order to get matrix in (1) satisfying dimentions restriction.

We put.

The corresponding hamiltonian system (16) for problem (21),(8) has the form

(22)

with initial conditions

(23)

The solutions were obtained numerically. On the Figure 1 and Figure 2 the graphs

of functions are exposed. The graphs illustrate convergence of the suggested method. The calculated corresponding average values (9) are exposed as well.

Acknowledgements

This work was supported by the Russian Foundation for Basic Research (projects no. 14-01-00168 and 14-01-00486) and by the Ural Branch of the Russian Academy of Sciences (project No. 15-16-1-11).

Cite this paper

Subbotina, N.N. and Krupennikov, E.A. (2016) Dynamic Program- ming to Identification Problems. World Jour- nal of Engineering and Technology, 4, 228-234. http://dx.doi.org/10.4236/wjet.2016.43D028

References