ABSTRACT

We present an improved hybrid genetic algorithm to solve the two-dimensional Euclidean traveling salesman problem (TSP), in which the crossover operator is enhanced with a local search. The proposed algorithm is expected to obtain higher quality solutions within a reasonable computational time for TSP by perfectly integrating GA and the local search. The elitist choice strategy, the local search crossover operator and the double-bridge random mutation are highlighted, to enhance the convergence and the possibility of escaping from the local optima. The experimental results illustrate that the novel hybrid genetic algorithm outperforms other genetic algorithms by providing higher accuracy and satisfactory efficiency in real optimization processing.

Keywords:

Genetic Algorithm, Hybrid Local Search, TSP

1. Introduction

Travelling Salesman problem (TSP) [1] is a well-known nondeterministic polynomial time (NP-Hard) problem and a typical example in combinatorial optimization researched in both operations research and theoretical computer science. TSP can be described as: Given a finite set of cities and a cost matrix, in which 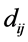denotes the cost (e.g., distance, money, time) of traveling from city 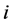to city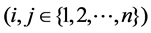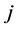, TSP aims to find the optimal tour 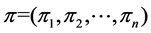that visits each city exactly once and eventually return to the starting city. The objective function of this linear programming problem in TSP is minimizing the sum value of the cost in

the valid tour:.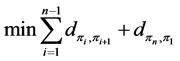

TSP and its variants transpire in a large variety of real-world applications such as vehicle routing, scheduling problems, integrated circuits designs, graph theory, gene ordering, and so on. Up to now, many literatures have reported that lots of techniques applied to those problems suffer from exponentially growing complexity for finding out an optimal solution. Various heuristic approaches have been conducted to obtain the global optimum or reasonable suboptimal solutions in solving TSP, such as Genetic Algorithm (GA) [2] [3], Simulated Annealing (SA) [4], Ant Colony Optimization (ACO) [5], Particle Swarm Optimization (PSO) [6], Tabu Search (TS) [7], Neural Network (NN) [8], and so on. Among all the evolutional algorithms, GA has paid more attention for its effectiveness compared to other algorithms in solving discrete combinatorial optimization problems. Furthermore, there are many researches [9] [10] [11] [12] on combining of GA with other evolutional algorithms to improve accuracy and efficiency in solving TSP.

In this paper, a novel hybrid GA (HGA), which incorporates the local search method into GA, is proposed to be as an effective heuristic approach for the two-dimensional Euclidean TSP. The proposed algorithm has the trade-off of preserving population diversity and preventing the premature convergence in the evolutionary processing. Some mechanisms are specifically designed and constructed to improve the quality of the final solutions with reasonable time-consuming for TSP, such as the elitist choice strategy, the local search crossover operator and the double-bridge random mutation. The proposed HGA is verified with some standard data benchmarks from TSPLIB [13]. In this work, we make the following contributions: 1) We introduce hybrid version of both algorithms with GA and the local search method as a promising method for TSP; 2) We conduct the experimental research to validate the effectiveness and efficiency of the HGA by a comprehensive comparison over other evolutionary algorithms.

The rest of this paper is organized as follows. Section 2 briefly introduces the traditional GA for TSP. Section 3 presents the description of the proposed HGA. Section 4 demonstrates the experimental results. Finally, Section 5 summarizes the paper and derives conclusions with the scope of future extension of this work.

2. Background

GA is an optimization model inspired by Darwinian evolution and was first proposed by John Holland in 1975 [2]. The traditional GA is an adaptive search technique to find the global optimum or quasi-optimum for optimization problems. The main operations using GA to solve TSP can be described as follows. Generally GA starts from a population of encoded feasible solutions, followed by evaluating the fitness function of individuals in the population. GA produces the next generation from the previous generation with three operations to exploit the search space, namely selection, crossover, and mutation operators. Selection operation typically chooses competitive individuals from the mating pool according to the survival strategy, such as roulette wheel selection, tournament selection, etc. Crossover and mutation operations primarily provide good searching diversification in the solution space.

The basic steps of GA are presented:

In solving the small-scale TSP, the traditional GA can provide the satisfactory optimal solution with an acceptable time-consuming. However, when the number of city nodes increases, the traditional GA is greatly challenged with respect to efficiency because of the stagnation behavior and premature convergence. Therefore, designing the effective operators in GA is considered to be a promising way to solve the medium-scale or large-scale TSP.

3. The Proposed Algorithm

In this paper, a novel heuristic HGA, which is a mechanism of combining GA with the local search strategy, is proposed to efficiently solve TSP. The proposed HGA incorporates the local search strategy into GA by the novel updating strategy which is the combination of the elitist choice strategy, the local search crossover operator and the double-bridge random mutation. It takes full advantage of exploration ability of GA and exploitation capability of the local search method to improve the quality of the optimum or sub-optimum solutions with reasonable time-consuming.

3.1. Initialization

In permutation encoding of TSP, the individual chromosome representing a feasible solution is encoded as a 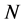dimensional integer vector 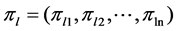(where 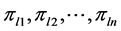represent 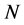consecutive city nodes in a complete valid tour with 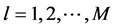(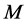is the population size)).An initial population of high quality can accelerate the population evolutionary processing of HGA to reach a satisfactory global optimum or suboptimal solutions. The generating process of the initial population in HAG is as follows: The 80% individuals of the initial population are randomly generated by random number generator and the other 20% individuals are created by the heuristics method based on the greedy strategy. The generating method of the initial population not only maintains the population diversity but also speed up convergence on the final solution by providing promising initial solutions.

3.2. Selection Operator

The mechanism of combing roulette wheel selection and elitist choice strategy is used as selection operator in HGA. These survival chromosomes with the best fitness value will have higher probabilities to be selected from the matting pool of the previous generation. In this paper, the fitness function is used as Equation 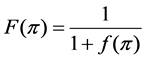(1).

(1)

3.3. Local Search Crossover Operator

Crossover operator is a vital factor which determines the characteristic optimization of HGA. Local search crossover operator, which preserves part of the good edge knowledge of the selected parent chromosomes obtained with the previous population, improves effectiveness and efficiency of HGA by exploring the more promising different regions of the solution space for TSP. The mechanism of the local search crossover operator is described in the following:

1) Randomly select two parent individuals (saying 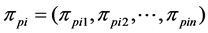and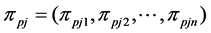) from the matting pool of the previous generation according to crossover probability.

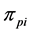
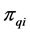
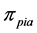
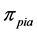
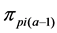
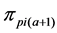
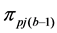
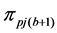
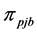
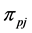
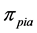
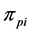
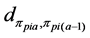
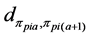
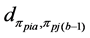
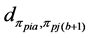
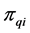
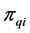
2) From the first parent individual, one gene node is selected randomly as the starting node of the offspring chromosome. For example, the node is selected as the start point of the new individual, then all the one-step neighborhood gene nodes of in both the two parents individuals are determined and they are, , , (the value of the node in is equal to that of the node in). Comparing the travelling distances between the current node and those one-step neighborhood gene nodes (, , ,) respectively, the nearest node to the current node in the neighborhood is selected and inserted into the sequence of. New added edge heuristically inherit minimum distance sub-path around the neighborhood of the current node from two parent individuals. Meanwhile, the added node is set as the current node in. For further expanding the searching range, the above neighborhood can be set as two-step or much more steps while the calculation and the computational time will be increasing.

3) Repeating the process of inserting the minimum distance edge around the neighborhood of the current node until the neighbor nodes of the current node has already been added the sequence of. Then, the nearest node to the current node will be sought in these remaining nodes that have not been added the sequence of.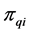

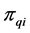
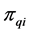
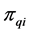
4) Repeating the above processing of the local search crossover operator until all of the nodes have been added into the sequence of. Thereby, one complete valid offspring chromosome is produced.

5) Another offspring chromosome 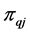is produced by using the same way. Finally, we produce two feasible offspring chromosomes from two parent individuals by local search crossover operator.

In every generation followed by the heuristic tour improvement, more refined individuals are exploited to moderately improve the population quality in approximating the global optimum or sub-optimum solutions as the execution progress.

3.4. Double-Bridge Random Mutation Operator

Double-bridge [14] random mutation operator is used to maintain the diversity of the population in HGA. It perturbs the original individual and increases the probability of generating better offspring through randomly modifying the gene values. Double- bridge random mutation operator plays an important role of avoiding the evolutionary process to trap into the local optimum and exploring an increasingly larger region of the solution space.

The HGA adequately utilizes the global exploring ability of GA and the efficiency of the local search method to obtain the satisfactory final solutions with acceptable time- consuming.

4. Experiments and Results

In these experiments, the computing platform is MATLAB R2012a on 2.30GHz CPU Intel Corei5-6300HQ and 4.00 GB RAM. For the comprehensive analysis of the feasibility and validity of the HGA, we carry out experiments on the two-dimensional symmetric Euclidean TSP instances from the best-known TSPLIB benchmark. Each instance is executed 20 times to obtain an average behavior for the method. 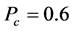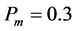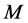The parameters of HGA are set as following: crossover probability; mutation probability. The population size is roughly equal to the number of cities. Those experimental results are shown in Table 1.

In Table 1, the performance indices in these experiments are described as follows:

1) Instance (Optimal): The name of instances and the corresponding length of optimal tour in parentheses. The name of each TSP instance has a suffix number that represents the number of city nodes of the instance.

2) Best: The best tour length with the 20 independent executions.

3) Ave.: The total average tour length of 20 trials.

4) Gap (%): The relative error of the length of the best tour to that of the optimal tour, which is formulated as Equation (2):

(2)

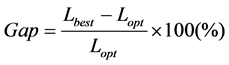
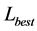
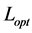
where is the best tour length among all the 20 trials and is the best-known optimal tour length of each instance so far.

5) Gen.: The average numbers of the iteration.

6) Time (s): the average computational time in seconds.

By observing the figures in Table 1, the results show that HGA could mostly works very well on the medium-scale TSP instances with up to 575 nodes. These average solutions are also stable and able to reach close to the optimum of each instance. The relative errors between the best tour lengths and TSPLIB optimum tour lengths: For Berlin52, Tsp225 and KroA150, HGA obtained better solutions can reach to the optimum solutions with high ratios of0.03, 1.15 and 1.98 respectively. Although the computational time depends on the different data characteristic of each instance, the time-con- suming increases with the increase of the case size to solve TSP in rationale and the bigger the size of a case, the greater the computing time. As the number of cities increases such as Tsp225, Lin318, Pr439 and Rat575, the average computational time increases with exponential order such as 552, 1214, 2264 and 4120. This reason is appropriate that the computational complexity will increase as well in executing local search crossover operator. All aspects of the statistical analysis represent the performances of the HGA including the final solution quality and the computational time. In general, Experimental results demonstrate that HGA can perform effectively and efficiently on the medium-scale TSP instance.

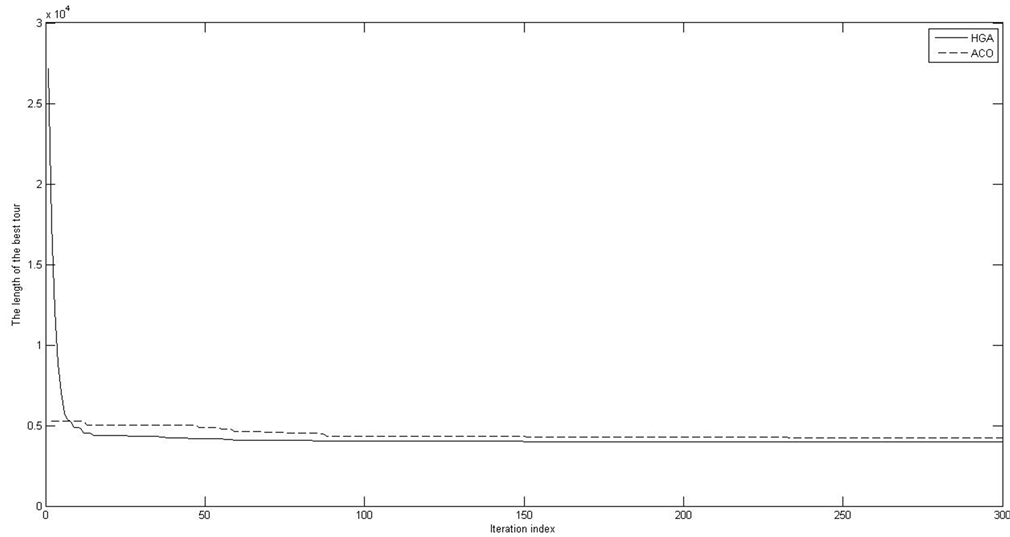
For the comparative experiment, there is an instance Tsp225 of the specific evolutionary processing obtained by HGA and the traditional ACO as shown in Figure 1. The diagram plots the lengths of the best tour obtained by those methods as a function of the iteration index.

For the fairness of the comparative results, the final best solution of each algorithm is allowed to evolve sufficiently. As it can be seen, the macroscopic behavior of those algorithms is presented by subsequently convergence rate and solution quality. For example, HGA converges at less than 150 iterations while the traditional ACO execute about 235iterations to achieve the same or worse results. Meanwhile, HGA can continue to converge to a better solution due to the local search ability of the competitive updating strategy. In addition, HGA performs 202 iterations on average and returns the final best solution with the relative error of only 1.15% from the optimal, while the traditional ACO executes about 247 iterations on average but returns the final best solutions with the relative error of 8.27% that is more than 7 times higher. The average tour length of HGA is 3991 while that of the traditional ACO is 4240 in the Tsp225 instance.

Therefore, HGA performs more effectively and efficiently than the traditional ACO in terms of the convergence rate and the solution quality.

For further to validate the effectiveness of HGA for TSP, we perform the comparative experiments to assess the contributions of HGA and other different algorithms. Table 2 shows the comparative results of HGA and those of the GA introduced in the article [9].

The results in Table 2 indicate that the average best tour lengths and the final tour lengths found by HGA are better than those obtained the GA [9] on the majority of instances. Meanwhile, the relative error of the best solution found by HGA is very higher than that of the GA [9] on most of instances. HGA has better solution quality than the GA [9] but suffers from a slightly slow speed. With the increase in the case size of TSP, we test HGA and the GA introduced in the article [10] on these TSP benchmarks with up to 442 cities. Table 3 also shows the comparative experimental results of HGA and the GA [10].

The results in Table 3 show that these improvements in the solution quality are statistically significant. The average solutions, the final solutions and the relative errors found by HGA are better than those obtained the GA [10] on these instances. Therefore, HGA outperforms those Genetic Algorithms in terms of the solution quality. HGA is a heuristic hybrid evolutionary algorithm with efficiency and effectiveness for solving TSP.

5. Conclusion

In this paper, a novel heuristic HGA integrating GA and the local search method in a

good symbiotic behavior is proposed and illustrated for the two-dimensional symmetric Euclidean TSP. The proposed HGA provides much better reasonable structure design to compensate for the balance between global and local search contributes to efficiently improve the evolutionary process in terms of the convergence rate and the solution quality. Experimental results demonstrate that HGA is a robust hybrid evolutionary algorithm to search the global optimum or sub-optimum solutions within reasonable computational time. Meanwhile, HGA works very well on the medium-scale TSP instances and outperforms the other GAs in the 4 section. As future research work, there is a lot of scope for development in HGA with large-scale TSP and their applications. We also plan to investigate extensions of the HGA for other complex optimization problems.

Acknowledgements

This work is jointly supported by the National Natural Science Foundation of China with grants No. 61473298 and No. 61473299.

Cite this paper

Lin, B., Sun, X.Y. and Salous, S. (2016) Solving Travelling Salesman Problem with an Improved Hybrid Genetic Algorithm. Journal of Computer and Communications, 4, 98-106. http://dx.doi.org/10.4236/jcc.2016.415009

References