ABSTRACT

In recent years, a growing number of math contents are available on the Web. When conventional search engines deal with mathematical expressions, the two-dimen- sional structure of mathematical expressions is lost, which results in a low performance of math retrieval. While the retrieval technology specifically designed for mathematical expressions is not mature currently. Aiming at these problems, an improved mathematical expression indexing and matching method was proposed through employing full text index method to deal with the two-dimensional structure of mathematical expressions. Firstly, through the fully consideration of LaTeX formulae’ characteristics, a feature representation method of mathematical expressions and a clustering method of feature keywords were put forward. Then, an improved inter-relevant successive trees index model was applied to the construction of the mathematical expression index, in which the cluster algorithm of mathematical expression features was employed to solve the problem of the quantity growth of the trees in processing large amount of formulae. Finally, the matching algorithms of mathematical expressions were given which provide four query modes called exact matching, compatible matching, sub-expression matching and fuzzy matching. In browser/server mode, 110027 formulae were used as experimental samples. The index file size was 29.02 Mb. The average time of retrieval was 1.092 seconds. The experimental result shows the effectiveness of the method.

Keywords:

Mathematical Expression Retrieval, Improved Math Index, Inter-Relevant Successive Tree, Clustering, Matching

1. Introduction

With the rapid increase of the amount of science and technology documents which contain many mathematical formulae with various expressing formats such as LaTeX and MathML in computers and network, finding and obtaining the required information according to the formulae in these documents becomes an urgent task in the fields of information retrieval and searching engine. However, the complex two-dimensional structure of mathematical expressions is often not properly handled in ordinary full-text search engine, which makes it necessary to research and develop special indexing and matching method for mathematical expressions.

At present, there are two kinds of strategies for realizing mathematical retrieval. The first category is to expand the existing text search engine system through transforming two-dimensional formulae into linear strings, such as LeActiveMath [1] [2], MathDex [3], EgoMath [4], DLMFSearch [5] and MIaS [6].

LeActiveMath [1] [2] is a system that enables people to use the searching tool to realize exploratory learning of mathematical knowledge. The system was based on the Lucene engine, and used OMDoc coding. The mathematical expressions are converted into symbolic stream, and the mathematical content is retrieved by matching the phrase in the symbolic flow. Because the query formula can appear in any layer of the matched formulae, the phrase match goes deep into each layer. The system also put forward a ranking mechanism to sort the search results, which makes the search results even better satisfy the needs of learners. EgoMath [4] for Wikipedia researched mathematical retrieval method. Many mathematical symbols in Wikipedia are expressed in TeX format, so EgoMath first considered the processing of mathematical formulae’ text to get a number of phrases. Then, by means of similarity description of the phrases, the standardization of formulae could be realized. The similarity description is similar to multiplication distributive law. Finding equal or similar descriptions in index can achieve similar retrieval. The method used in this system increases the semantic information and reduce the ambiguity of the formulae.

The second category for realizing math retrieval is to design retrieval model for mathematical expressions specially, such as MathWebSearch [7] and WikiMirs [8]. MathWebSearch [7] could solve the problem of formulae retrieval from the semantic aspect of formulae. Based on the structure and semantics of the expressions, the index was constructed by using the substitution tree. Instead of the real terms, the substitution tree stored the substitutions. In the retrieval stage, the two-dimensional structure and the text form of the expression are searched respectively, and the intersection of the two retrieval results is obtained. Finally, the system shows the result of sorted intersection. The system considered the structure and semantic of expressions comprehensively, and analyzed the elements in the expressions sufficiently. WikiMirs [8] was also for Wikipedia to research mathematical retrieval method. It consists of four major components, preprocessor, tokenizer, indexer, and ranker. The preprocessor is to extract the LaTeX tag from the XML file, and then the formula is standardized; the presentation tree parser in tokenizer aims at parsing LaTeX labels into an internal presentation tree. Based on the normalized presentation tree, terms are extracted using a hierarchical generalization technique; the inverted index is used to store the key information; through calculating the similarity score of the keywords in the query expression and index file and the matching degree of key words in different levels sufficiently, the system shows the ranking result. In this system, the mathematical expression of the LaTeX form was transformed by the tree to construct the index, and the similar search of formulae was realized.

In addition, there are other individuals or institutions to study the retrieval method of mathematical expressions. Kristianto et al. [9] used the mathematical expressions in the form of Presentation MathML to construct the index for the related description of each formula. There are two kinds of text information in the mathematical retrieval system, which are textual content and textual description. The textual description was extracted with machine learning methods SVM automatically. The dependency graph enriches the textual description of the target expression, and improves the accuracy of the retrieval result. Aiming at the similarity retrieval of mathematical expressions in web pages and PDF documents, Lin et al. [10] constructed the index and retrieval model of mathematical expressions. Mathematical expressions are represented by semi- operator tree, which combines layout presentation tree and semantic operator tree, and according to the tree, semantic rich technology is proposed. Extract key words from semi-operator tree, and then construct index for generalized keywords. In the index structure stage, there are two index files called the index file of terms and formulae and the index file of terms and documents. By calculating the similarity between the formula and the document, the correlation degree between the retrieval result and the query expression is increased. Schellenberg et al. [11] constructed index of LaTeX formulae by improving substitution tree, and introduced the concept of insertion bias, which could correct search results according to the baseline size of an expression. In the retrieval stage, according to the layout of the symbols to find the correlation expressions, the system can achieve sub-expression query, which can enrich the search results. Zhou et al. [12] built a hierarchical index model for LaTeX formulae called Treap data structure layer and inverted index layer. Through the design and implementation of the retrieval algorithm which is adapted to the index, it can realize the two matching modes of the exact match and the structure match, which has a good adaptability to the two-dimensional structure of the mathematical expression. Aiming at the problem of mathematical expressions retrieval based on layout, Stalnaker et al. [13] extracted symbol pairs from the symbol layout tree to construct inverted index. The system still needs to be improved. Aiming at complex structure and rich semantics of formulae, Xu et al [14] came up with semantic indexing method by improving the N-gram method which is suitable for mathematical expressions. In combination with the computer algebra system, the method realizes the equivalent search. Akiko et al. [15] used the mathematical expressions of the presentation and content MathML form. The feature description is the combination of the noun phrase in the formulae and the expression in the same sentence, and it is used to train these features with SVM. Used a variety of methods to build index, it can achieve the exact matching and similarity matching.

In a word, the method of extending the function of the existing text search engine for math retrieval need to convert formulae into character strings, which cannot provide a complete searching function for formulae. Another strategy of realizing math retrieval that designs the special index and corresponding matching algorithm is still not mature. This paper proposes an improved mathematical expressions index method based on the inter-relevant successive tree [16] [17] [18] and corresponding searching algorithm which integrated the above two strategies through employing full text index method to deal with the two-dimensional structure of mathematical expressions. The characteristics of the method is utilizing the extracted formulae features to form the relationships as predecessor and successor, for constructing math index in the mode of inter-relevant successive tree.

2. The Improved Math Index

The inter-relevant successive tree (ISTR) [16] [17] [18] is a full-text index model which can effectively connect the predecessor and successor nodes for expressing the relationships of characters in text. It has the characteristics of high speed of index creating and matching with high space efficiency. There are two layers in the tree called the root node layer and the leaf node layer. The leaf nodes which express the current character in a tree are linked to the root node of next tree corresponding to next character position, which forms the full text index.

In [19], we proposed a formulae indexing and retrieving method based on ISTR. In the method, the hash values of feature keywords served as the node values in the tree. Root nodes also stored other information about the keywords. In the retrieval stage, matching algorithms with exact matching, compatible matching, sub-expression matching and fuzzy matching modes were realized. It achieved relatively ideal results in experiments. In order to overcome the problem exist in the model that the retrieval efficiency is influenced by the large quantity of the trees when indexing great amount of mathematical expressions, an improved method is proposed in this paper by processing the feature keywords especially.

The improved ISTR increases a clustering layer on the original two layers structure to form a mathematical index structure with three layers. These three layers are clustering layer, branch layer and successor layer.

The first layer is the clustering layer which clusters the root nodes of the original ISTR into several classes to avoid the problem that the increasing number of trees in the index structure may cause the large expansion of the index scale. The nodes in the layer are called the cluster nodes.

The second layer is the branch layer which contains the root node in the original ISTR. The nodes in the layer are called the branch nodes.

The third layer is the successor layer which consists of the leaf nodes in the original ISTR which is called the successor nodes now.

The improved index tree structure is shown in Figure 1. The shadow part of the figure indicates the improved new structure, similarly in the following figure.

As can be seen in the Figure 1, each branch of the tree has a number, and the nodes in the tree are orderly arranged. The numbers of the branches in the first layer indicate the positions of the branch nodes in the cluster nodes, which are called the branch node number. The numbers in the second layer branches indicate the positions of the successor nodes in the branch nodes, which are called the successor node number. The successor node not only records its branch node number, but also records the number of the nodes in the cluster node, which lays the foundation for realizing math retrieval.

3. Clustering of Mathematical Expressions Feature

3.1. Feature Extraction of Mathematical Expressions

Suppose that the mathematical expressions are described in LaTeX format. Take the FDS (Formula Description Structure) defined in [20] [21] as the basis of the retrieval feature of mathematical expressions.

Definition 1. EF is a 5-tuple (Key, Oper, Level, Flag, Prestr) which is used as the retrieval feature of formulae. The components of it are defined as follows.

Ÿ Key is the identifier of the item of mathematical expression. The last one of key is “#” which indicates the end of the expression.

Ÿ Oper stores the item corresponding to the key. The Oper value is “Null” when the key has no operator.

Ÿ Level is the layer number of the item in the formulae. The value of layer on the reference layer is 0. The farther the layer from the baseline, the large the Level value has.

Ÿ Flag stores the relationship between current item and its control item which has the higher level in the formulae. Its value is 1 - 8 means the relationships between two items to be above, superscript, right, subscript, below, contains, left-superscript and left-subscript respectively. The value 0 means the symbol is located in the reference layer.

Ÿ Prestr indicates the keyword of the control item of current item. When the Flag value is 0, Prestr is “Null” .

Algorithm 1 shows the procedure for obtaining the EF of an expression.

Algorithm 1. Extraction of the EF of formula.

1. Sort the items of formula according to their Level value in ascending order.

2. Sort the items in the same level on the basis of Flag in ascending order.

3. Merge the symbols which have the same values of Level, Flag, Prestr, and extract the operators in these items.

For example, the LaTeX expression of “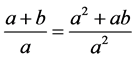” is “\[\frac{{a+b}}{a} = \frac{{{a^2}+ab}}{{{a^2}}}\]”. The EF of it is shown in Table 1. Among them, “\one\frac” and “\two\frac” are the serial number of the same character “\frac” in the expression.

3.2. Feature Clustering of Mathematical Expressions

ISTR is an index model for one dimensional Chinese characters and strings. When the indexing object is Chinese characters, a single Chinese character is served as a node in the tree that can express words or sentences, etc. When the indexing object is strings, a single character is used as a node in the tree. All of the above two kinds of circumstances can be represented a large amount of text information with a small number of trees. However, mathematical expressions are arranged in two-dimensional structures. The combination of their operators and operands is myriads of changes. If the ISTR is used to construct math index directly, the number of trees would be very large which will influence the efficiency of math retrieval. So, it is necessary to cluster the feature keywords of mathematical expressions before constructing the index to reduce the number of trees. The clustering rules are as follows.

Rule 1: For key₁ and key₂, if and only if the oper₁ = oper₂, key₁ and key₂ are aggregated in the same class. In the improved ISTR, each tree represents a class, and key₁ and key₂ are inserted into the same tree when building index.

Take the feature in Table 1 as an example. The value of Key (except “#”) is represented by k₁, k₂... k₇. The value of Oper “(\frac, = \frac)” is described as O₁, “(+)” is described as O₂ and “(Null)” is described as O₃.The clustering results are shown in Figure 2.

4. Construction of Mathematical Index

4.1. Expressing Rules of Formulae in ISTR

The nodes’ positions and tags’ order of operators and operands of formulae in the improved ISTR are as follows.

Rule 1: The operators and operands located at the same level with the same flag and identifier are stored in the same node.

Rule 2: If the operators and operands are at different levels, mark the lower level firstly, and then mark the higher level. The operators and operands are stored in different nodes.

Rule 3: The controlled items (operands) of a controlling item (operator) are at the same level with different flags are stored in different nodes. The operands’ tag order is above, superscript, right, subscript, below, contains, left-superscript and left-subscript successively. When there is no symbol at a flag, it is not marked.

Rule 4: If the operators or operands are located at the same level with the same flag but different identifier, mark them according to the order of their LaTeX description, and their located nodes are also changed.

The above rules can be used not only independently but also synthetically. We make a detailed description of these rules with the example of mathematical expressions.

Left-right structure: the expression is “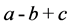”. Its LaTeX description is “\[a − b + c\]”. The position of nodes and the tag sequence are shown in Figure 3.

Up-down structure: the expression is “”. Its LaTeX description is “\[\frac{x}{y}\]”. The position of nodes and the tag sequence are shown in Figure 4.

Containment structure: the expression is “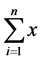” and its LaTeX description is “\[\sum\limits{i=1}^nx \]”. The position of nodes and the tag sequence are shown in Figure 5.

Corner structure: the expression is “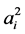” and its LaTeX description is “\[a_i^2\]”. The position of nodes and the tag sequence are shown in Figure 6.

When a variety of these operators appear on the same level of an expression, whether or not the same, the tag sequence will be strictly in accordance with the above rules. Only when the symbols of a flag are completed stored can the next item with different flag be processed.

4.2. Index Information in ISTR

For realizing mathematical expression retrieval with a high performance, we modified the ISTR based math index in [19] through adding a clustering layer to improve the searching efficiency. The index structure is shown in Figure 7.

The distribution of each element of formulae features EF in the improved ISTR is as follows: the first layer of clustering is based on Oper feature. The formulae with the same operator are clustered into the same class. The class of this layer is connected to the branch node in the next layer which has the same value of key in the Oper feature. In the second layer, not only the value of Key feature but also the values of flag and prestr of the key are stored. The third layer only stores the value of Key feature.

4.3. Index Construction Algorithm

Definition 2: Suppose key_i and key_j to be any two keywords which are adjacent each other in a mathematical expression. key_i is called the predecessor of key_j, and key_j is called the successor of key_i. The successor of the last keyword is “#” denoting the end of keywords. key_ikey_j is called double key.

The successor nodes store the number information of double key in the next tree. The algorithm for constructing the mathematical expression index is as follows.

Algorithm 2: Improved math index construction

Input: A LaTeX formula

Output: The improved ISTR index

Step 1: Read EF of mathematical expression and count the frequency of two adjacent keywords.

Step 2: According to the Oper in EF, find the cluster node in current index. If Oper exists in current index, go to step 4. Otherwise, go to step 3.

Step 3: Create new cluster node, that is creating a new tree.

Step 4: Analyze the tree which employ Oper as root node. If it contains the predecessor information of double key in its branch nodes, go to step 6; Otherwise, go to step 5.

Step 5: Create a new branch, and ascertain branch node number.

Step 6: Traverse successor nodes of predecessor as branch node to search the successor of double key. If the successor exists in successor nodes, ascertain successor node number, and go to step 8. Otherwise go to step 7.

Step 7: Insert a new leaf node, and ascertain successor node number.

Step 8: According to the branch node number and successor node number, insert the successor node information.

Step 9: End.

4.4. Case Analysis

The features of the “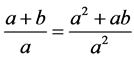” are listed in Table 1, and its ISTR structures are as follows Figure 8.

When the information of current formula already exists in the index structure, a new node is no longer generated.

ISTR structures of “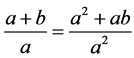”, “”, “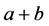” 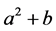are shown in Figure 9.

In index structure, the nodes in the tree also store the other feature information of the formulae. The index structure of several formulae is shown in Figure 10.

5. The Algorithm of Mathematical Expression Retrieval

In the improved ISTR which added the clustering layer, the number of search trees is reduced, and the retrieval time is shortened, so the retrieval efficiency is improved.

In the exact retrieval mode, when there is only one keyword in query expression feature, we only need to determine whether the branch node contains the keyword. If it is true, output the document information which matched Flag and Prestr features. When the number of keywords in query expression feature is two and more than two, its algorithm is as follows.

Algorithm 3: Accurate retrieval algorithm

1: Input: Query math expression

2: Output: Math matching result

3: Define List Q_EF(term_key, term_oper, term_flag, term_prestr) is query math expression feature

Tree_node(cluster_node, branch_node, successor_node, T_flag, T_prestr, document information) is the node of a tree in the database

4: for each term_iterm_j in Q_EF

5: if then

6: if then

7: if then

8: Select document information that conform to

9: end if

10: end if

11: end if

12: end for

In addition to the accurate retrieval, there are three kinds of matching models, which are compatible matching, sub-expression matching and fuzzy matching. Compatible retrieval is based on the algorithm 3 to cancel the restrictions of the first keyword’ Flag and Prestr values, and the corresponding document information is the result of the compatibility matching. Sub-expression matching is to extract the sub-structure features of the query expression based on extracting the features of the query expression, and to accurate matching for sub-structure features that do not contain serial number. Fuzzy matching is a consistent search for the sub-structure of the query expression.

6. Experiments Results

The experiment is carried on a server with CPU of 2.50 GHz, RAM of 8 GB, Windows sever 2012, SQLServer 2012 and a PC as a browser with CPU of 2.50 GHz, and 8 GB RAM. The experiment is carried on 110027 formulae from Wikipedia. In the data sets, the number distribution of formulae containing the different number of keywords is shown in Figure 11.

6.1. Clustering Result

With the growth of the number of indexed formulae, the number of feature keywords and cluster nodes is shown in Figure 12.The number of cluster nodes in the index structure is the number of improved trees and the number of keywords is the number of original trees. As can be seen from Figure 12, the number of keywords is three times the number of cluster nodes, which indicates that the improved ISTR controls the infinite growth of the number of trees, and plays a role in clustering.

6.2. Space Efficiency

The sizes of index files are shown in Table 2. With the growth of the number of indexed formulae, the size of the index files grows. Because of the clustering function of the cluster layer, the same nodes are stored only once. So the growth rate of the index file and the file size are acceptable. Table 3 lists the sizes of the index files in [10].

6.3. Time Efficiency

320 formulae were randomly selected to retrieve the efficiency of the experiment, and

the results are shown in Table 4.The retrieval efficiency data of [10] are shown in Table 5. With the growth of the number of indexed formulae, retrieval time of the method increases. Because the number of the formulae grows, the number of nodes in the tree continues to grow, and the judgment time of the nodes is lengthened, which influences the retrieval time. The experimental data show that the time efficiency of the proposed method is within the acceptable range.

6.4. Contrast Experiment with the Original Index Structure

The contrast experiment between the improved math index and the original one in two aspects of space and time are shown in Figure 13 and Figure 14 respectively. From the sight of space, the improved index model added clustering layer in the original tree structure, so the store information is much more than the original index model, and the index files are also larger than the original index files. From the view of time, because of the added clustering layer, speed up the search speed of the tree. The retrieval efficiency of the algorithm is higher than that of the original index model. From Figure 13 and Figure 14, the original index model improvement has obtained the certain effect in this paper.

7. Conclusions

In this paper, on the basis of the discussion on various kinds of methods of indexing construction, an improved indexing and matching method based on the inter-relevant successive tree was proposed. Facing the fact that the different keywords may contain the same operator, a layer of cluster nodes was added to the inter-relevant successive tree. This not only avoids the infinite increase of the number of trees in the index structure, but also reduces the search time and improves the retrieval efficiency. The effectiveness of the method was verified by experiments. However, there are some shortages in the method. Due to the limitation of the experimental data, the estimation

of the data diversity is insufficient. Moreover, the characteristic of special formulae needs to be further strengthened.

The future work is to add to the sorting module of the results. It can improve the rationality of the order of search results, and then improve the practical application of the system.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 61375075), the Natural Science Foundation of Hebei Province (Grant No. F2012201020; F2013201134) and the Project of Human Resources and Social Security of Hebei Province (Grant No.JRS-2016-1090).

Cite this paper

Liu, H.C., Tian, X.D., Tian, B.J., Yang, F. and Li, X.F. (2016) An Improved Indexing and Matching Method for Mathematical Expressions Based on Inter-Relevant Successive Tree. Journal of Computer and Communications, 4, 63- 78. http://dx.doi.org/10.4236/jcc.2016.415006

References