Open Access Library Journal
Vol.03 No.11(2016), Article ID:72091,13 pages
10.4236/oalib.1103068
Properties of Fuzzy Length on Fuzzy Set
Jehad R. Kider, Jaafar Imran Mousa
Department of Mathematics and Computer Applications, School of Applies Sciences, University of Technology, Bagdad, Iraq

Copyright © 2016 by authors and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 15, 2016; Accepted: November 13, 2016; Published: November 17, 2016
ABSTRACT
The definition of fuzzy length space on fuzzy set in this research was introduced after the studies and discussion of many properties of this space were proved, and then an example to illustrate this notion was given. Also the definition of fuzzy convergence, fuzzy bounded fuzzy set, and fuzzy dense fuzzy set space was introduced, and then the definition of fuzzy continuous operator was introduced.
Subject Areas:
Fuzzy Mathematics
Keywords:
Fuzzy Length Space on Fuzzy Set, Fuzzy Convergence, Fuzzy Cauchy Sequence of Fuzzy Point, Fuzzy Bounded Fuzzy Set and Fuzzy Continuous Operator

1. Introduction
Zadeh in 1965 [1] introduced the theory of fuzzy sets. Many authors have introduced the notion of fuzzy norm in different ways [2] - [9] . Cheng and Mordeson in 1994 [10] defined fuzzy norm on a linear space whose associated fuzzy metric is of Kramosil and Mickalek type [11] as follows:
The order pair 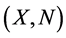 is said to be a fuzzy normed space if X is a linear space and N is a fuzzy set on
is said to be a fuzzy normed space if X is a linear space and N is a fuzzy set on  satisfying the following conditions for every
satisfying the following conditions for every  and
and .
.
(i)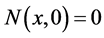 , for all
, for all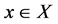 .
.
(ii) For all ,
, 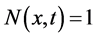 if and only if
if and only if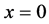 .
.
(iii)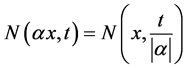 , for all
, for all 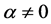 and for all
and for all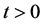 .
.
(iv) For all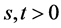 ,
,  where
where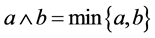 .
.
(v)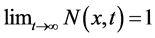 .
.
The definition of continuous t-norm was introduced by George and Veeramani in [12] . Bag and Samanta in [2] modified the definition of Cheng and Mordeson of fuzzy norm as follows:
The triple 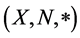 is said to be a fuzzy normed space if X is a linear space,
is said to be a fuzzy normed space if X is a linear space, 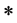 is a continuous t-norm and N is a fuzzy set on
is a continuous t-norm and N is a fuzzy set on ![]() satisfying the following conditions for every
satisfying the following conditions for every ![]() and
and![]() .
.
(i)![]() , for all
, for all![]() .
.
(ii) For all![]() ,
, ![]() if and only if
if and only if![]() .
.
(iii) ![]() for all
for all![]() .
.
(iv) For all![]() ,
,![]() .
.
(v) For![]() ,
, ![]() is continuous.
is continuous.
(vi)![]() .
.
The definition of fuzzy length space is introduced in this research as a modification of the notion of fuzzy normed space due to Bag and Samanta. In Section 1, we recall basic concepts of fuzzy set and the definition of continuous t-norm. Then in Section 2 we define the fuzzy length space on fuzzy set after we give an example; then we prove that every ordinary norm induces a fuzzy length, and also the definition of fuzzy open fuzzy ball, fuzzy convergent sequence, fuzzy open fuzzy set, fuzzy Cauchy sequence, and fuzzy bounded fuzzy set is introduced. In Section 3, we prove other properties of fuzzy length space. Finally in Section 4, we define a fuzzy continuous operator between two fuzzy length spaces. Also we prove several properties for fuzzy continuous operator.
2. Basic Concept about Fuzzy Set
Definition 2.1:
Let X be a classical set of object, called the universal set, whose generic elements are denoted by x. The membership in a classical subject A of X is often viewed as a characteritic function ![]() from X onto {0, 1} such that
from X onto {0, 1} such that ![]() if
if ![]() and
and ![]() if
if![]() , {0, 1} is called a valuation set. If a valuation set is allowed to be real interval [0, 1] then A is called a fuzzy set which is denoted in this case by
, {0, 1} is called a valuation set. If a valuation set is allowed to be real interval [0, 1] then A is called a fuzzy set which is denoted in this case by ![]() and
and ![]() is the grade of membership of x in
is the grade of membership of x in![]() . Also, it is remarkable that the closer the value of
. Also, it is remarkable that the closer the value of ![]() to 1, the more belong to
to 1, the more belong to![]() . Clearly,
. Clearly, ![]() is a subset of X that has no sharp boundary. The fuzzy set
is a subset of X that has no sharp boundary. The fuzzy set ![]() is completely characterized by the set of pairs:
is completely characterized by the set of pairs:
![]() [1] .
[1] .
Definition 2.2:
Suppose that ![]() and
and ![]() are two fuzzy sets in Y. Then
are two fuzzy sets in Y. Then
(i)![]() .
.
(ii)![]() .
.
(iii)![]() .
.
(iv)![]() .
.
(v) ![]() [4] .
[4] .
Definition 2.3:
Suppose that ![]() and
and ![]() be two fuzzy sets in
be two fuzzy sets in ![]() and
and ![]() respectively then
respectively then ![]() is a fuzzy set whose membership is defined by:
is a fuzzy set whose membership is defined by:
![]() [8] .
[8] .
Definition 2.4:
A fuzzy point p in Y is a fuzzy set with single element and is denoted by ![]() or
or![]() . Two fuzzy points
. Two fuzzy points ![]() and
and ![]() are said to be different if and only if
are said to be different if and only if ![]() [11] .
[11] .
Definition 2.5:
Suppose that ![]() is a fuzzy point and
is a fuzzy point and ![]() is a fuzzy set in Y. then
is a fuzzy set in Y. then ![]() is said to belongs to
is said to belongs to ![]() which is written by
which is written by ![]() [2] .
[2] .
Definition 2.6:
Suppose that h is a function from the set ![]() into the set
into the set![]() . Let
. Let ![]() be a fuzzy set in W then
be a fuzzy set in W then ![]() is a fuzzy set in V its membership is:
is a fuzzy set in V its membership is:
![]() for all d in V. Also when
for all d in V. Also when ![]() is a fuzzy set in V then
is a fuzzy set in V then ![]() is a fuzzy set in W its membership is given by:
is a fuzzy set in W its membership is given by: ![]() when
when ![]() and
and ![]() otherwise [5] .
otherwise [5] .
Proposition 2.7:
Suppose that ![]() is a function. Then the image of the fuzzy point
is a function. Then the image of the fuzzy point ![]() in V, is the fuzzy point
in V, is the fuzzy point ![]() in W with
in W with ![]() [11] .
[11] .
Definition 2.8:
A binary operation ![]() is said to be t-norm (or continuous triangular norm) if
is said to be t-norm (or continuous triangular norm) if ![]() the conditions are satisfied:
the conditions are satisfied:
(i)![]() .
.
(ii)![]() .
.
(iii)![]() .
.
(iv) If ![]() and
and ![]() then
then ![]() [12] .
[12] .
Examples 2.9:
When ![]() and
and ![]()
![]() then
then ![]() is a continuous t- norm [10] .
is a continuous t- norm [10] .
Remark 2.10:
![]() , there is t such that
, there is t such that ![]() and for every r, there is e such that
and for every r, there is e such that![]() , where p, q, t, r and e belongs to [0, 1] [12] .
, where p, q, t, r and e belongs to [0, 1] [12] .
Definition 2.11:
Let ![]() be a fuzzy set in Z and let τ be a collection of all subset fuzzy set in
be a fuzzy set in Z and let τ be a collection of all subset fuzzy set in![]() . then
. then ![]() is called a fuzzy topological space on the fuzzy set
is called a fuzzy topological space on the fuzzy set ![]() if (i)
if (i)![]() .
.
(ii) ![]() for any
for any![]() ,
,![]() .
.
(ii)![]() , for
, for ![]() [10] .
[10] .
Proposition 2.12:
Let ![]() be an arbitrary operator and
be an arbitrary operator and ![]() and
and![]() . Then
. Then ![]() if and only if
if and only if ![]() [9] .
[9] .
3. On Fuzzy Length Space
First we introduce the main definition in this paper.
Definition 3.1:
Let X be a linear space over field ![]() and let
and let ![]() be a fuzzy set in X. let
be a fuzzy set in X. let ![]() be a t- norm and
be a t- norm and ![]() be a fuzzy set from
be a fuzzy set from ![]() to [0,1] such that:
to [0,1] such that:
(FL1) ![]() for all
for all![]() .
.
(FL2) ![]() if and only if
if and only if![]() .
.
(FL3) ![]() where
where![]() .
.
(FL4)![]() .
.
(FL5) ![]() is a continuous fuzzy set for all
is a continuous fuzzy set for all ![]() and
and![]() .
.
Then the triple ![]() is called a fuzzy length space on the fuzzy
is called a fuzzy length space on the fuzzy![]() .
.
Definition 3.2:
Suppose that ![]() is a fuzzy length space on the fuzzy set
is a fuzzy length space on the fuzzy set ![]() then
then ![]() is con-
is con-
tinuous fuzzy set if whenever ![]() in
in ![]() then
then ![]() that is
that is![]() .
.
Proposition 3.3:
Let ![]() be a normed space, suppose that
be a normed space, suppose that ![]() be a fuzzy set in Y. Put
be a fuzzy set in Y. Put![]() . Then
. Then![]() , is a fuzzy normed space.
, is a fuzzy normed space.
Proof:
Let ![]() and
and ![]() then
then
1) ![]() for all
for all![]() .
.
2)![]() .
.
3)![]() .
.
4)![]() .
.
Hence![]() , is a fuzzy normed space.
, is a fuzzy normed space.
Example 3.4:
Suppose that ![]() is a normed space and assume that
is a normed space and assume that ![]() is a fuzzy set in Y. Put
is a fuzzy set in Y. Put
![]() for all
for all![]() . Define
. Define![]() .
.
Then ![]() is a fuzzy length space on the fuzzy set
is a fuzzy length space on the fuzzy set![]() , is called the fuzzy length induced by
, is called the fuzzy length induced by![]() .
.
Proof:
To prove ![]() is a fuzzy length space on the fuzzy set
is a fuzzy length space on the fuzzy set ![]() we must prove the five conditions of Definition 3.1:
we must prove the five conditions of Definition 3.1:
(FL1) Since ![]() for all
for all ![]() so
so ![]() for all
for all![]() , where
, where![]() .
.
(FL2) It is clear that ![]() for each
for each ![]() if and only if
if and only if![]() .
.
(FL3) If ![]() then for each
then for each![]() ,
, ![]() for each
for each![]() .
.
(FL4) ![]() for each
for each![]() , where
, where![]() .
.
(FL5) ![]() is continuous since
is continuous since ![]() is a continuous function.
is a continuous function.
Hence ![]() is a fuzzy length space on the fuzzy
is a fuzzy length space on the fuzzy![]() .
.
Definition 3.5:
Let ![]() be a fuzzy set in X, and assume that
be a fuzzy set in X, and assume that ![]() is a fuzzy length space on the
is a fuzzy length space on the
fuzzy![]() . Let
. Let![]() . So
. So ![]() is said to be
is said to be
a fuzzy open fuzzy ball of center ![]() and radius r.
and radius r.
We omitted the proof of the next result since it is clear.
Proposition 3.6:
In the fuzzy length space ![]() on the fuzzy
on the fuzzy![]() , Let
, Let ![]() and
and ![]() with
with ![]() and
and![]() . Then either
. Then either ![]() or
or ![]() .
.
Definition 3.7:
The sequence ![]() in a fuzzy length space
in a fuzzy length space ![]() on the fuzzy
on the fuzzy ![]() is fuzzy converges to a fuzzy point
is fuzzy converges to a fuzzy point ![]() if for a given
if for a given![]() ,
, ![]() , then there exists a positive number K such that
, then there exists a positive number K such that ![]()
Definition 3.8:
The sequence ![]() in a fuzzy length space
in a fuzzy length space ![]() on the fuzzy
on the fuzzy ![]() is fuzzy converges to a fuzzy point
is fuzzy converges to a fuzzy point ![]() if
if ![]()
Theorem 3.9:
The two Definitions 3.8 and 3.7 are equivalent.
Proof:
Let the sequence ![]() is fuzzy converges to a fuzzy point
is fuzzy converges to a fuzzy point![]() , then for a given
, then for a given ![]() then there is a number K with
then there is a number K with ![]() for all
for all![]() , and hence
, and hence![]() . Therefore
. Therefore ![]() when
when![]() .
.
To prove the converse, let ![]() when
when![]() .
.
Hence when![]() , there is K such that
, there is K such that ![]()
![]() .
.
So![]() . Therefore
. Therefore ![]() by Definition 3.7. ∎
by Definition 3.7. ∎
Lemma 3.10:
Suppose that ![]() is a fuzzy length space on the fuzzy
is a fuzzy length space on the fuzzy![]() . Then
. Then ![]() for any
for any![]() .
.
Proof:
Let![]() , then
, then ![]() where
where ![]()
![]()
Lemma 3.11:
If ![]() is a fuzzy length space. Then,
is a fuzzy length space. Then,
(a) The operator ![]() is continuous.
is continuous.
(b) The operator ![]() is continuous.
is continuous.
Proof:
If ![]() and
and ![]() as
as ![]() then
then
![]()
Hence the operator addition is continuous function.
Now if![]() , and
, and ![]() and
and ![]() then
then
![]()
And this proves (b).
Definition 3.12:
Suppose that ![]() is a fuzzy length space and
is a fuzzy length space and ![]() then
then ![]() is called fuzzy open if for every
is called fuzzy open if for every ![]() there is
there is![]() . A subset
. A subset ![]() is called fuzzy closed if
is called fuzzy closed if ![]() is fuzzy open.
is fuzzy open.
The proof of the following theorem is easy and so is omitted.
Theorem 3.13:
Any ![]() in a fuzzy length space
in a fuzzy length space ![]() is a fuzzy open.
is a fuzzy open.
Definition 3.14:
Suppose that ![]() is a fuzzy length space, and assume that
is a fuzzy length space, and assume that![]() . Then the fuzzy closure of
. Then the fuzzy closure of ![]() is denoted by
is denoted by ![]() or
or ![]() and is defined by
and is defined by ![]() is the smallest fuzzy closed fuzzy set that contains
is the smallest fuzzy closed fuzzy set that contains![]() .
.
Definition 3.15:
Suppose that ![]() is a fuzzy length space, and assume that
is a fuzzy length space, and assume that![]() . Then
. Then ![]() is said to be fuzzy dense in
is said to be fuzzy dense in ![]() if
if ![]() or
or![]() .
.
Lemma 3.16:
Suppose that ![]() is a fuzzy length space, and assume that
is a fuzzy length space, and assume that![]() , Then
, Then ![]() if and only if we can find
if and only if we can find ![]() in
in ![]() such that
such that![]() .
.
Proof:
Let![]() , if
, if ![]() then we take the sequence of fuzzy points of the type
then we take the sequence of fuzzy points of the type![]() . If
. If![]() , we construct the sequence of fuzzy points
, we construct the sequence of fuzzy points ![]() as follows:
as follows:![]() for each
for each![]() .
.
The fuzzy ball ![]() contains
contains ![]() and
and ![]() since
since ![]()
Conversely assume that ![]() and
and ![]() then
then ![]() or the fuzzy open fuzzy ball of
or the fuzzy open fuzzy ball of ![]() contains
contains ![]() with
with![]() , so
, so ![]() is a fuzzy limit fuzzy point of
is a fuzzy limit fuzzy point of![]() . Hence
. Hence![]() .
.
4. Other Properties of Fuzzy Length on Fuzzy Set
Theorem 4.1:
Suppose that ![]() is a fuzzy length space and let that
is a fuzzy length space and let that![]() , then
, then ![]() is fuzzy dense in
is fuzzy dense in ![]() if and only if for any
if and only if for any ![]() we can find
we can find ![]() with
with ![]() for some
for some![]() .
.
Proof:
Let ![]() be a fuzzy dense in
be a fuzzy dense in![]() , and
, and ![]() so
so ![]() then using 3.16 we can find
then using 3.16 we can find ![]() with
with ![]() for all
for all![]() . Take
. Take![]() ,
,![]() .
.
To prove the converse, we must prove that![]() . Let
. Let ![]() then there is
then there is ![]() such that
such that![]() , where
, where![]() . Now take
. Now take ![]() such that
such that ![]() for each
for each![]() . Hence we have a sequence of fuzzy points
. Hence we have a sequence of fuzzy points![]() such that
such that ![]() for all
for all ![]() that is
that is ![]() so
so ![]() +
+
Definition 4.2:
Suppose that ![]() is a fuzzy length space. A sequence of fuzzy points
is a fuzzy length space. A sequence of fuzzy points ![]() is said to be a fuzzy Cauchy if for any given
is said to be a fuzzy Cauchy if for any given![]() , there is a positive number K such that
, there is a positive number K such that ![]() for all
for all![]() .
.
Theorem 4.3:
If ![]() is a sequence in a fuzzy length space
is a sequence in a fuzzy length space ![]() with
with ![]() then
then ![]() is fuzzy Cauchy.
is fuzzy Cauchy.
Proof:
If ![]() is a sequence in a fuzzy length space
is a sequence in a fuzzy length space ![]() with
with![]() . So
. So
for any ![]() there is an integer K such that
there is an integer K such that ![]() for all
for all
![]() . Now by Remark 2.10 there is
. Now by Remark 2.10 there is ![]() such that
such that![]() . Now for each
. Now for each![]() , we have
, we have
![]()
Hence ![]() is fuzzy Cauchy. ∎
is fuzzy Cauchy. ∎
Definition 4.4:
Suppose that ![]() is a sequence in a fuzzy length space
is a sequence in a fuzzy length space ![]() let (
let (![]() ) be a sequence of positive numbers such that
) be a sequence of positive numbers such that![]() , then the sequence
, then the sequence ![]() of fuzzy points is said to be a subsequence of
of fuzzy points is said to be a subsequence of![]() .
.
Theorem 4.5:
Suppose that ![]() is a sequence in a fuzzy length space
is a sequence in a fuzzy length space![]() , if it is fuzzy converges to
, if it is fuzzy converges to ![]() then every subsequence
then every subsequence ![]() of
of ![]() is fuzzy converges to
is fuzzy converges to![]() .
.
Proof:
Let ![]() be a sequence of fuzzy points in
be a sequence of fuzzy points in ![]() fuzzy converges to
fuzzy converges to ![]() then
then![]() . But
. But ![]() is fuzzy Cauchy by Theorem (4.3) hence,
is fuzzy Cauchy by Theorem (4.3) hence, ![]() as
as ![]() and
and![]() . Now
. Now
![]() .
.
Taking the limit to both sides as ![]() we get
we get
![]()
Hence, ![]() fuzzy converges to
fuzzy converges to![]() , since
, since ![]() was an arbitrary subsequence of
was an arbitrary subsequence of![]() . Therefore all subsequence
. Therefore all subsequence ![]() of
of ![]() is fuzzy converges to
is fuzzy converges to![]() .
.
Proposition 4.6:
Let ![]() be a fuzzy Cauchy sequence in a fuzzy length space
be a fuzzy Cauchy sequence in a fuzzy length space ![]() con-
con-
tains a ![]() such that
such that![]() , then
, then ![]() fuzzy converges to
fuzzy converges to
![]() .
.
Proof:
Assume that ![]() is a fuzzy Cauchy sequence in
is a fuzzy Cauchy sequence in![]() . So for all
. So for all![]() ,
, ![]() there is an integer K such that
there is an integer K such that ![]() whenever
whenever
![]() . Let
. Let ![]() be a subsequence of
be a subsequence of ![]() and
and![]() . It follows that
. It follows that ![]() whenever
whenever![]() . Since (
. Since (![]() ) is increasing sequence of positive integers. Now
) is increasing sequence of positive integers. Now
![]()
Letting![]() , we have
, we have![]() .
.
Hence, the sequence ![]() it fuzzy converges to
it fuzzy converges to![]() .
.
Definition 4.7:
Suppose that ![]() is a fuzzy length space and
is a fuzzy length space and![]() . Then
. Then ![]() is said to be fuzzy bounded if we can find q,
is said to be fuzzy bounded if we can find q, ![]() 1 such that,
1 such that,![]() .
.
Lemma 4.8:
Assume that ![]() is a fuzzy length space. If a sequence
is a fuzzy length space. If a sequence ![]() with
with ![]() then it is fuzzy bounded and its fuzzy limit is unique.
then it is fuzzy bounded and its fuzzy limit is unique.
Proof:
Let![]() , that is for a given r > 0 then we can find K with
, that is for a given r > 0 then we can find K with ![]() for all
for all![]() .
.
Put![]() .
.
Using Remark 2.10 we can find ![]() with
with![]() . Now for
. Now for ![]()
![]()
Hence ![]() is fuzzy bounded in
is fuzzy bounded in![]() .
.
Suppose that ![]() and
and![]() . Therefore
. Therefore ![]() and
and![]() . Now
. Now ![]() . By taking the limit to both sides, as
. By taking the limit to both sides, as![]() ,
,![]() . So
. So![]() , hence
, hence![]() .
.
Definition 4.9:
Suppose that ![]() is a fuzzy length space on the fuzzy set
is a fuzzy length space on the fuzzy set![]() . Then
. Then ![]() is said to be a fuzzy closed fuzzy ball with center
is said to be a fuzzy closed fuzzy ball with center ![]() and radius q,
and radius q,![]() .
.
The proof of the following lemma is clear and hence is omitted.
Lemma 4.10:
Any ![]() in a fuzzy length space
in a fuzzy length space ![]() is a fuzzy closed fuzzy set.
is a fuzzy closed fuzzy set.
Theorem 4.11:
A fuzzy length space ![]() is a fuzzy topological space.
is a fuzzy topological space.
Proof:
Suppose that ![]() is a fuzzy length space. Put
is a fuzzy length space. Put ![]() if and only if there is
if and only if there is ![]() such that
such that![]() . We prove that
. We prove that ![]() is a fuzzy topology on
is a fuzzy topology on![]() .
.
(i) Clear that ![]() and
and![]() .
.
(ii) let ![]() and put
and put![]() . We will show that
. We will show that![]() , let
, let ![]() then
then ![]() for each
for each![]() . Hence there is
. Hence there is ![]() such that
such that![]() . Put
. Put ![]() so
so ![]() for all
for all![]() , this implies that
, this implies that ![]() for all
for all![]() . Therefore,
. Therefore, ![]() , thus
, thus![]() .
.
(iii) Let![]() . put
. put![]() . We will show that
. We will show that![]() . Let
. Let![]() , then
, then ![]() for some
for some![]() , since
, since ![]() then there exists
then there exists ![]() such that
such that![]() , Hence
, Hence![]() . This prove that
. This prove that![]() . Hence,
. Hence, ![]() is a fuzzy topological space.
is a fuzzy topological space. ![]() is called the fuzzy topology induced by
is called the fuzzy topology induced by![]() .
.
Definition 4.12:
A fuzzy length space ![]() is said to be a fuzzy Hausdorff space if for any
is said to be a fuzzy Hausdorff space if for any ![]() such that
such that ![]() we can find
we can find ![]() and
and ![]() for some
for some ![]() and
and ![]() such that
such that![]() .
.
Theorem 4.13:
Every fuzzy length space ![]() is a fuzzy Hausdorff space.
is a fuzzy Hausdorff space.
Proof:
Assume that ![]() is a fuzzy length space and let
is a fuzzy length space and let ![]() with
with![]() .
.
Put![]() , for some
, for some![]() . Then for each s,
. Then for each s, ![]() , we can find q such that
, we can find q such that ![]() by Remark 2.10. Now consider the two fuzzy open fuzzy balls
by Remark 2.10. Now consider the two fuzzy open fuzzy balls ![]() and
and![]() . Then
. Then ![]() Since if there exists
Since if there exists![]() . Then
. Then
![]()
is a contradiction, hence ![]() is a fuzzy Hausdorff space.
is a fuzzy Hausdorff space.
5. Fuzzy Continuous Operators on Fuzzy Length Spaces
In this section, we will suppose ![]() is fuzzy set of X and
is fuzzy set of X and ![]() be fuzzy set of Y where X and Y are vector space.
be fuzzy set of Y where X and Y are vector space.
Definition 5.1:
Let ![]() and
and ![]() be two fuzzy length space on fuzzy set
be two fuzzy length space on fuzzy set ![]() and
and ![]() respectively, let
respectively, let ![]() then The operator
then The operator ![]() is said to be fuzzy continuous at
is said to be fuzzy continuous at![]() , if for every
, if for every ![]() there exist
there exist ![]() such that
such that ![]() whenever
whenever ![]() satisfying
satisfying![]() . If T is fuzzy continuous at every fuzzy point of
. If T is fuzzy continuous at every fuzzy point of![]() , then T it is said to be fuzzy continuous on
, then T it is said to be fuzzy continuous on![]() .
.
Theorem 5.2:
Let ![]() and
and ![]() be two fuzzy length space, let
be two fuzzy length space, let![]() . The operator
. The operator ![]() is fuzzy continuous at
is fuzzy continuous at ![]() if and only if whenever a sequence of fuzzy points
if and only if whenever a sequence of fuzzy points ![]() in
in ![]() fuzzy converge to
fuzzy converge to![]() , then the sequence of fuzzy points
, then the sequence of fuzzy points ![]() fuzzy converges to
fuzzy converges to![]() .
.
Proof:
Suppose that the operator ![]() is fuzzy continuous at
is fuzzy continuous at ![]() and let
and let ![]() be a sequence in
be a sequence in ![]() fuzzy converge to
fuzzy converge to![]() . Let
. Let ![]() be given. By fuzzy continuity of T at
be given. By fuzzy continuity of T at![]() , then there exists
, then there exists ![]() such that whenever
such that whenever ![]() and
and![]() , implies
, implies![]() . Since
. Since ![]()
then we can find K with ![]() such that
such that![]() . Therefore when
. Therefore when
![]() implies
implies![]() . Thus
. Thus![]() .
.
Conversely, assume that every sequence ![]() in
in ![]() fuzzy converging to
fuzzy converging to ![]() has the property that
has the property that![]() . Suppose that T is not fuzzy continuous at
. Suppose that T is not fuzzy continuous at![]() . Then there is
. Then there is ![]() and for which no
and for which no![]() ,
, ![]() can satisfy the require-
can satisfy the require-
ment that ![]() and
and ![]() implies
implies![]() . This means that for every
. This means that for every ![]() there exists
there exists ![]() such that
such that ![]() but
but![]() . For every
. For every![]() , there exist
, there exist ![]() such that
such that![]() , but
, but
![]() . The sequence
. The sequence ![]() fuzzy converges to
fuzzy converges to ![]() but the sequence
but the sequence ![]() does not fuzzy converge to (
does not fuzzy converge to (![]() ). This contradicts the assumption that every sequence
). This contradicts the assumption that every sequence ![]() in
in ![]() fuzzy converging to
fuzzy converging to ![]() has the property that
has the property that![]() . Therefore the assumption that T is not fuzzy continuous at
. Therefore the assumption that T is not fuzzy continuous at ![]() must be false.
must be false.
Definition 5.3:
Let ![]() and
and ![]() be two fuzzy length spaces let
be two fuzzy length spaces let ![]() and let
and let ![]() the fuzzy point
the fuzzy point ![]() is a fuzzy limit of
is a fuzzy limit of ![]() written by
written by ![]() whenever
whenever ![]() if for every
if for every ![]() there is
there is ![]() such that
such that ![]() when
when ![]() and
and![]() .
.
Proposition 5.4:
Let ![]() and
and ![]() be two fuzzy length spaces, let
be two fuzzy length spaces, let ![]() and
and![]() . Suppose that
. Suppose that ![]() is fuzzy limit fuzzy point of
is fuzzy limit fuzzy point of![]() . Then
. Then ![]() if and only if for every sequence
if and only if for every sequence ![]() in
in ![]() such that
such that ![]() and
and![]() .
.
Proof: the argument is similar that of Theorem (5.3) and therefore is not included.
Proposition 5.5:
An operator T of the fuzzy length space ![]() into a fuzzy length space
into a fuzzy length space ![]() is fuzzy continuous at the fuzzy point
is fuzzy continuous at the fuzzy point ![]() if and only if for every
if and only if for every ![]() there exist
there exist ![]() such that
such that![]() .
.
Proof: the operator ![]() is fuzzy continuous at
is fuzzy continuous at ![]() if and only if for every
if and only if for every ![]() there exist
there exist ![]() such that
such that ![]() for all
for all ![]() satisfying
satisfying ![]() i.e.
i.e. ![]() implies
implies ![]() or
or ![]() this is equivalent to the condition
this is equivalent to the condition
![]() .
.
Theorem 5.6:
An operator ![]() is fuzzy continuous if and only if
is fuzzy continuous if and only if ![]() is fuzzy open in
is fuzzy open in ![]() for all fuzzy open
for all fuzzy open ![]() of
of ![]() where
where ![]() and
and ![]() are fuzzy length space.
are fuzzy length space.
Proof:
Suppose that T is fuzzy continuous operator and let ![]() be fuzzy open in
be fuzzy open in ![]() we show that
we show that ![]() is fuzzy open in
is fuzzy open in![]() . Since
. Since ![]() and
and ![]() are fuzzy open, we may suppose that
are fuzzy open, we may suppose that ![]() and
and![]() .
.
Let ![]() then
then![]() . Since
. Since ![]() is fuzzy open, then there is
is fuzzy open, then there is ![]() such that
such that![]() , since T is fuzzy continuous at
, since T is fuzzy continuous at ![]() by proposition 4.5 for this
by proposition 4.5 for this ![]() there exist
there exist ![]() such that
such that![]() .
.
Thus, every fuzzy point ![]() of
of ![]() is an interior fuzzy point and so
is an interior fuzzy point and so ![]() if a fuzzy open in
if a fuzzy open in![]() .
.
Conversely, suppose that ![]() is fuzzy open in
is fuzzy open in ![]() for any fuzzy open
for any fuzzy open ![]() of
of![]() . Let
. Let ![]() for each
for each![]() , the fuzzy ball
, the fuzzy ball ![]() is fuzzy open in
is fuzzy open in ![]()
since ![]() it follows that there exist
it follows that there exist ![]() such that
such that ![]() by proposition 5.5, it follows that T is fuzzy continuous.
by proposition 5.5, it follows that T is fuzzy continuous.
Theorem 5.7:
An operator ![]() is fuzzy continuous on
is fuzzy continuous on ![]() if and only if
if and only if ![]() is fuzzy closed in
is fuzzy closed in ![]() for all fuzzy closed
for all fuzzy closed ![]() of
of![]() .
.
Proof:
Let ![]() be a fuzzy closed subset of
be a fuzzy closed subset of ![]() then
then ![]() is fuzzy open in
is fuzzy open in ![]() so that
so that ![]() is fuzzy open in
is fuzzy open in ![]() by theorem 4.6 but
by theorem 4.6 but ![]() so
so ![]() is fuzzy closed in
is fuzzy closed in![]() .
.
Conversely, suppose that ![]() is fuzzy closed in
is fuzzy closed in ![]() for all fuzzy closed subset
for all fuzzy closed subset ![]() of
of![]() . But the empty fuzzy set and the whole space
. But the empty fuzzy set and the whole space ![]() are fuzzy closed fuzzy set. Then
are fuzzy closed fuzzy set. Then ![]() is fuzzy open in
is fuzzy open in ![]() and
and ![]() is fuzzy in
is fuzzy in![]() . Since every fuzzy open subset of
. Since every fuzzy open subset of ![]() is of the type
is of the type![]() , where
, where ![]() is suitable fuzzy closed fuzzy set, it follows by using theorem 5.6, that T is fuzzy continuous.
is suitable fuzzy closed fuzzy set, it follows by using theorem 5.6, that T is fuzzy continuous.
Theorem 5.8:
Let ![]() and
and ![]() and
and ![]() be three fuzzy length spaces let
be three fuzzy length spaces let ![]() and
and ![]() be fuzzy continuous operator. Then the composition
be fuzzy continuous operator. Then the composition ![]() is a fuzzy continuous operator from
is a fuzzy continuous operator from ![]() into
into![]() .
.
Proof:
Let ![]() be fuzzy open subset of
be fuzzy open subset of![]() . By theorem (5.6),
. By theorem (5.6), ![]() is a fuzzy open subset of
is a fuzzy open subset of ![]() and another application of the same theorem shows that
and another application of the same theorem shows that ![]() is a fuzzy open subset of
is a fuzzy open subset of![]() , since
, since ![]() it follows from the same theorem again that (
it follows from the same theorem again that (![]() ) is a fuzzy continuous.
) is a fuzzy continuous.
Theorem 5.9:
Let ![]() and
and ![]() be two fuzzy length spaces let
be two fuzzy length spaces let![]() , then the following statements are equivalent.
, then the following statements are equivalent.
(i) T is fuzzy continuous on![]() .
.
(ii) ![]() For all subset
For all subset ![]() of
of![]() .
.
(iii) ![]() For all subset
For all subset ![]() of
of![]() .
.
Proof: (i) ⇒ (ii)
Let ![]() be a subset of
be a subset of![]() , since
, since ![]() is a fuzzy closed subset of
is a fuzzy closed subset of![]() ,
, ![]() is fuzzy closed in
is fuzzy closed in![]() . Moreover
. Moreover ![]() and so
and so![]() .
.
[Recall that ![]() is the smallest fuzzy closed fuzzy set containing
is the smallest fuzzy closed fuzzy set containing![]() ].
].
Proof: (ii) ⇒ (iii)
Let ![]() be a subset of
be a subset of![]() , then if
, then if![]() , we have
, we have ![]() and
and ![]() thus
thus![]() .
.
Proof: (iii) ⇒ (i)
Let ![]() be a fuzzy closed fuzzy set in
be a fuzzy closed fuzzy set in ![]() and fuzzy set
and fuzzy set![]() . By theorem (4.7), it is sufficient to show that
. By theorem (4.7), it is sufficient to show that ![]() is a fuzzy closed in
is a fuzzy closed in![]() , that is,
, that is, ![]() Now
Now ![]() so that
so that![]() .
.
6. Conclusion
In this research the fuzzy length space of fuzzy points was defined as a generalization of the definition of fuzzy norm on ordinary points. Based on the defined fuzzy length, most of the properties of the ordinary norm were proved.
Cite this paper
Kider, J.R. and Mousa, J.I. (2016) Properties of Fuzzy Length on Fuzzy Set. Open Access Library Journal, 3: e3068. http://dx.doi.org/10.4236/oalib.1103068
References
- 1. Zadeh, L. (1965) Fuzzy Sets. Information and Control, 8, 338-452.
https:/doi.org/10.1016/S0019-9958(65)90241-X
- 2. Bag, T. and Samanta, S. (2003) Finite Dimensional Fuzzy Linear Spaces. Fuzzy Mathematics, 11, 678-705.
- 3. Bag, T. and Samanta, S. (2006) Fixed Point Theorems on Fuzzy Normed Spaces. Information Sciences, 176, 2910-2931.
https:/doi.org/10.1016/j.ins.2005.07.013
- 4. Wang, C.X. and Ming, M. (1993) Continuity and Boundness Mappings between Fuzzy Normed Spaces. Fuzzy Mathematics, 1, 13-24.
- 5. Felbin, C. (1992) Finite Dimensional Fuzzy Normed Linear Spaces. Fuzzy Sets and Systems, 48, 239-248.
https:/doi.org/10.1016/0165-0114(92)90338-5
- 6. Golet, I. (2010) On Generalized Fuzzy Normed Spaces and Coincidence Theorems. Fuzzy Sets and Systems, 161, 1138-1144.
https:/doi.org/10.1016/j.fss.2009.10.004
- 7. Kider, J. (2012) New Fuzzy Normed Spaces. Baghdad Science Journal, 9, 559-564.
- 8. Kider, J.R. (2013) Completeness of the Cartesian Product of Two Complete Fuzzy Normed Spaces. Engineering and Technology Journal, 31, 310-315.
- 9. Kider, J.K. and Hussain, Z.A. (2014) Continuous and Uniform Continuous Mapping on Standard Fuzzy Metric Spaces. Engineering and Technology Journal, 32, 1111-1119.
- 10. Cheng, S. and Mordeson, J. (1994) Fuzzy Linear Operators and Fuzzy Normed Linear Spaces. Bulletin of Calcutta Mathematical Society, 86, 429-436.
- 11. Kramosil, O. and Michalek, J. (1975) Fuzzy Metrics and Statistical Metric Spaces. Kybernetika, 11, 326-334.
- 12. George, A. and Veeramani, P. (1994) On Some Results in Fuzzy Metric Spaces. Fuzzy Sets and Systems, 64, 395-399.
https:/doi.org/10.1016/0165-0114(94)90162-7





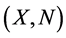 is said to be a fuzzy normed space if X is a linear space and N is a fuzzy set on
is said to be a fuzzy normed space if X is a linear space and N is a fuzzy set on  satisfying the following conditions for every
satisfying the following conditions for every  and
and .
.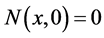 , for all
, for all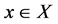 .
. ,
,  if and only if
if and only if .
. , for all
, for all  and for all
and for all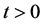 .
.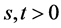 ,
,  where
where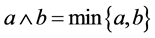 .
.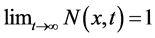 .
.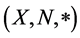 is said to be a fuzzy normed space if X is a linear space,
is said to be a fuzzy normed space if X is a linear space, 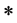 is a continuous t-norm and N is a fuzzy set on
is a continuous t-norm and N is a fuzzy set on 





















































































































































































































































































































































































































































































































































































































































































































