ABSTRACT

Experimental results of linear and curved conducting thin wires’ disintegration under high power but low energy electrical discharges are reported. Microscopic origin of the anomalous energy release is traced into the lattice interaction with the strong transient radiation field causing the appearance of a strong Stark effect out of the polarization of the metallic surface. The possible role of the wire curvature is also explored with the resonant transmission line numerical method for the Schrödinger equation.

Subject Areas:

Electric Engineering

Keywords:

Battery Explosions, Curved Wire Disintegration, Schrödinger Dynamics

1. Introduction

The recently reported dramatic events on the case of the Samsung Note 7 product failure call for attention in a variety of phenomena that may become ubiquitous in the future in the case of highly compacted portable electronics requiring high energy density sources. Such failures cause a dear financial burden and a severe disruption in further technological development thus calling attention to the exact mechanisms responsible and the prevention and security measures to be taken.

In the particular case of the battery explosion effect, one notices the prehistory of this tracing a timeline of at least a decade. It is reported that by 2006, one in 200.000 Li-ion batteries breakdown caused a similar recall of almost six million parts by the Sony manufacturer [1] . Standard explanations offered regard certain statistically expected defects in the complex industrial assembly procedures that are unable to eliminate all metallic dust which can subsequently cause a short circuit event at some unforeseen time. It was assumed that such particles may accumulate due to self-charging causing overheating.

Recently, the phenomenon of thermal runaway and subsequent explosion in Li-ion batteries was investigated via NMR techniques at Cambridge and results revealed a different, more complex picture due to the formation of dendrites from Li metal fibers [2] [3] . This is supposedly associated with rapid charging or violations in the voltage- current allowed charger characteristics leading to extreme chemical reactions inside the batteries. Another recent attempt in replicating this effect was reported [4] where X-rays were used to record the effect while thermalization was artificially produced via particle bombardment. While real conditions may differ significantly and often batteries explode even hours after charging, it remains to examine the exact role of dendritic formation and its possible relation with the phenomena analyzed in the next section.

In the next sections, we report an alternative explanation based on both the dendrite formation as well as the case of curved wiring during packaging as in the case of the Samsung product due to severe size limitations out of the need to have a non-removable battery inside each device. Our hypothesis is backed with experimental evidence based on previous work by the authors on a similar case of long, thin conductor explosions caused high power and high voltage rapid discharges leading to current bursts. In a previous sequence of papers, we reported on a theoretical model [5] and a number of experiments [6] [7] with a very low internal resistance generator of high power electrical pulses but low energy spectral content causing fragmentation of long thin, copper wires. In what follows, we use the analogy between curved dendrites and long thin wires as a basis for our further consideration.

Wire explosions were first systematically studied in the 60s with the appearance of a study from a fuse engineer [8] showing photographic evidence of fragments from said forces during extreme circuit breaking instead of the expected melting. Later on, people in the industry used very high energy pulses to cause the obliteration and plasmification of copper wires for a variety of purposes. Taylor [9] performed certain experiments and observed the plasma formation around exploding copper wires and tried to explain the type of current flow including the plasma conductivity. Wienterberg [10] was the first to propose an unorthodox interpretation of the energy release in terms of an excited quantum vacuum. The last serious attempt to an orthodox interpretation comes for Molokov [11] [12] [13] who used a macroscopic approximation based on thermoelasticity and refused the validity of pinch effects. While these have been shown to result in strong oscillations and longitudinal forces in open unconnected wires, they still cannot explain the case of wires with clamped ends as is the case of all closed circuits.

In the present review, we attempt to generalize the questions posed at the original papers in the case of arbitrarily curved long wires. In section 2, we report on additional experimental evidence of complete explosive disintegration of long thin copper wires emitting bright white light with low energy input thus exhibiting some anomalous energy release. In section 3, we propose a theoretical model for observed anomalous energy release due to a strong Stark effect and we compare with recent similar results from Coulomb explosions. We also examine the role of curvature that appeared to make a difference in the energy release during the experiments and numerically show the lowering of the energy eigenvalues of a simplified electron gas model via direct numeric calculation in an appendix. In sections 4 and 5, analysis of the transient free electron concentration on thin curved wires is presented.

2. Evidence of Anomalous Energy Release in Disintegrating Conductors

The pulse generator used was the same as in [7] based on a capacitor bank of 4 capacitors in total each of 3 μF of total capacity up to 12 μF. A special thyristor and a digital programmable controller was used to deliver a sequence of pulses of at least 1 kV peak power with a time constant not exceeding 1.2 μs and with a very low internal resistance of the order of some mΩs. This causes a current inrush of the order of tens of kA for several long thin copper wires.

At lengths in the range of 20 to 30 cm, we observed a persistent phenomenon of bright white light emission and subsequent disintegration where all fragments also kept emitting white light during their trajectories away from the electrodes as shown by photographic evidence. This was recorded with a 35 fps camera and the results are presented in Figure 1(a) and Figure 1(b). In Figure 2(a) we also saw the captured ending phase which is followed by a reddish ball suggesting plasma formation. This was again verified with the use of a plastic tube surrounding the wire as shown in Figure 2(b). Notably, the last fragments are much less than the original wire mass while it proved extremely difficult to collect any remnants of the initial copper mass with current equipment. Additionally, we have observational evidence for cases of curved wires giving much stronger explosions than straight ones which we will attempt to justify in the theoretical analysis of the following sections.

In future experiments we intend to capture the complete sequence of events during disintegration with the use of a 500 to 1000 fps high speed camera. Results will be reported in a subsequent publication. We also note in passing that certain deterioration in the intensity of the explosions was observed most probably due to subsequent deterioration of the quality in the Thyristor’s operational condition. This is solely due to the physico-chemical properties of solid state devices that cannot always withstand the high switching demands and may develop hot spots. Higher quality electronics will have to be used in future tests to ameliorate all side effects.

It should be noticed that in all such experiments the electric field developed on the wire’s surface is quite high. This is associated with the very high rise time and it depends

on the power dissipated on the wire which is of the order of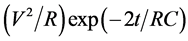. For values of 1 kV voltage, R ~ 0.1Ω and 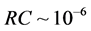used in the particular installation we may currently reach power levels of at least 10 MW albeit very rapidly decreasing and reaching zero in no more than 10 msecs. The associated strong electric fields are known to be also associated with certain nonlinear effects regarding the material polarizability and other properties that require further theoretical analysis. In the next section 3 we provide some strong theoretical arguments in favor of a microscopic explanation of the anomalous behavior.

3. Probability of Electromagnetically Excited Transmutation Events in Thin Conducting Wires

While others have already studied extensively various aspects of the conductor’s thermalization and thermo-plastic effects, we are still lacking a true microscopic and quantum mechanical treatment of the behavior of the material in terms of the lattice structure and its free electron wave function.

Any linear or curved thin conducting wire can be defined by a length variable s(r, θ, z) in a three dimensional space, where 0 ≤ s ≤ L and can be considered as one dimensional quantum wire trap for its own free electrons. The eigenfunctions of its free electrons will be zeros at its terminal points s = 0 and s = L. In case of a linear thin wire with zero curvature one can approximate the wire as an infinite potential well. 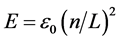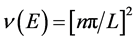From standard textbooks, it is known that the z eigenfunctions will be a set of sinusoidal standing waves with respective energy eigenvalues given as where with a total of possible values. In case of thin curved wires the interference of the geometric potential appearing in their Schrödinger equations according to [14] , necessarily alters the form of the eigenfunctions that are not in general sinusoidal as will be shown in the next section.

In any case inside the thin quantum wire trap the enclosed free electrons will form transient standing waves whenever a transient external voltage excitation is exerted by some external source. When the external voltage potential is terminated, the standing transient motion of free electrons will decay due to scattering effects of the free electrons with the metallic lattice, referred macroscopically as Ohmic losses. In any moment and at any point (s) of a thin wire near thermodynamic equilibrium, the expected value of the wire’s free electron concentration for metals will be given as a function of the associated Fermi energy via 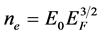where 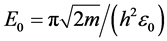for a total drift current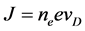. For Copper, with E_F = 7 eV we have n_e ~ 0.84 x 10²⁹ e/m³. We remind though that these are all approximations near thermal equilibrium and their validity could break down near an extreme situation as far from equilibrium as that in the case of abrupt, transient high power excitations.

Macroscopically the expected value, of a sea of free electrons, defines its electric charge linear density at the point s(r, θ, z). Variation of this density by an external abrupt voltage excitation will cause any linear or curved wire to act temporarily as an antenna with respective frequencies related to length and the speed of light of the standing electric waves given approximately by 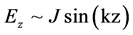with 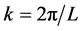for the fundamental harmonic. In case of relatively low energy voltage excitation we may consider the first eigenfunction harmonic as the most important.

This approach was used in our previous studies [1] [2] [3] for the case of fragmentation of thin linear wires, using standard macroscopic electromagnetic theory. In the case of curved wires where there is no general theoretical approach in electromagnetism for the excited standing electric waves under external transient voltage which calls for an alternative treatment using the simplifying approximation of a large potential well. Due to the transient standing waves on the thin wires, the free electrons are temporarily concentrated in certain points of maximum expectation values of their quantum eigenfunctions. These transient phenomena are vivid at least during the voltage excitation period.

In the case of our experiments with a capacitor bank of 12 μF overall capacitance, the ohmic resistance of the thin wire was approximately 80 mΩ. Thus the discharge time constant was approximately ~10⁻⁶ sec. The period of the lowest eigenfunction was calculated by the speed of light and the length of the thin wire in a range of 20 to 30 cm, thus giving a macroscopic period of the order of 10⁻⁹⁽GHz range), which is enough time for many cycles of standing waves of free electrons of the wire during the voltage discharge.

The transiently concentrated free electrons in a certain point can create huge local electric voltage potentials, acting on their nearby atoms trapped in the lattice. Such very strong potentials can be the cause of an extremely large Stark effect on nearby atoms. In such a case, there is a high probability for some the atomic nuclei to be temporarily stripped of all their electrons and in the absence of a shielding barrier the probability of them being affected by rapidly moving electrons in their vicinity also increases. A first numerical study of such a mechanism for straight wires only, has been reported elsewhere [15] .

We have also noticed similar strong disintegration phenomena taking place on experiments with metallic strips. Although the eigenfunctions of two dimensional metal traps in three dimensional spaces, of arbitrary boundaries are not known, we can assume that there will be several points of strong free electron concentration that are capable of creating strong Stark effects and the anticipated nuclear transmutations.

4. Analysis of Thin Curved Wires as Quantum Potential Wells

As also noticed in Section 2, one of the strangest effects observed concerns an intensification of explosive effects when curvature was present in the wires. It was difficult to systematically experiment on this issue further due to a subsequent decrease of the quality of the presently used solid state capacitors at the moment. In the present section, we are giving theoretical and numerical evidence on the possible significance of such curvature in combination with very high power electrical excitations.

Without any external electric field acting on the wire, free electrons will be affected by the wire’s curvature and some deviation from the original smooth envelope of their eigenfunctions should be expected. According to recent work [14] the Schrödinger equation for a curved one dimensional wire developed along its parametric curve s with is given by

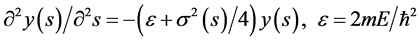(1)

In (1), the parametric representation of the one dimensional wire the standard curvature is given by the local radius R via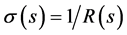. This, homogeneous, linear 2^nd order ODE can be solved with the aid of the Resonant Transmission Line (RTL) technique previously introduced by Papageorgiou as reviewed in [15] and used already in a variety of other 2^nd order ODEs and PDEs. A short presentation of the method is given in Appendix A.

Following the analysis there, equation (1) reduces to the case of a transmission line with which give the local propagation constant at each point as

(2)

We take every small part of the curved wire of length δs as equivalent to a T-qua- drupole of impedances Z_B and Z_P with reference to Figure 3, being given as

(3)

We also take the terminal impedances of the equivalent line at the boundaries s =0 and L to be infinite so as to make y(s) zero at these points.

We now consider a varying curvature which introduces an equivalent effective potential of geometric origin and we compute the resulting eigenvalues and eigenfunctions. To this purpose, we divide the wire in small parts of length δs along which we may take the curvature to be practically constant. Each such element is then equivalent to the T-quadrupole of Figure 7 parametrized as in (2) and (3). The whole wire is then equivalent to a lossless transmission line along s, made by the succession of T-quadrupoles terminated at infinite impedances. We now have the freedom to choose any arbitrary intermediate point and calculate the respective “left” and “right” impedances as functions of the energy ε. Eigenvalues will then correspond to the roots of the function.

The respective eigenfunctions are then directly obtained for each and any eigenvalue from the values of the respective currents of the T-quadrupoles through the application of a Transfer Matrix on a set of initial conditions as explained in App. A, in the form

(4)

In (4) we used the abbreviation. Initial values are taken as V₀ =1 and I₀ = 0. For infinitesimal displacements, (4) can always be approximated as

(5)

Some remarkable statistical properties of the resulting dynamical system in terms of its transfer matrix are mentioned in App. A. The trajectory obtained this way contains the representation of the eigenfunction from the current values at the

chosen points of the curved wire. We may then isolate any maximal points

representing points of maximal expected value for the electron concentration. We then naturally anticipate that under an external strong excitation there will be an increasing tendency of free electrons to be present at these points. This is further discussed in the last section.

Using the codes presented in App. B, we performed a numerical exploration of the effects of curvature in the one dimensional wire model. Since the first harmonic with the lower energy eigenvalue appears to be the most important for the energy transfer mechanism, as well as for the maximal concentration of the free electron density, we concentrate on this case. Higher states with higher energies are considered more difficult to excite given the low energy content of our exerted electrical pulses. For the first harmonic we expect to have two zeros at the terminal points (0, L) and a single maximum in the middle, with curvature or not. We chose to examine a case of length L = 1, subdivided in three areas as

(6)

The middle part corresponds to a hemicycle with radius while φ in (6) stands for the arc angle. Results of our simulations are shown in Figure 4 and Figure 5 where the first harmonic is plotted as a function of the characteristic ratio λ = L₁/L. In the first plot, we chose a fixed value of λ = 0.28 while in the second the eigenvalues are shown as a function of the φ angle for the same ratio. The resulting distorted eigenfunction are shown in Figure 6 and Figure 7 respectively.

5. Discussion and Conclusions

In the present report, we analyzed the case of abrupt energy release during disintegration phenomena taking place in long thin conducting paths with curvature. We hypothesize that similar mechanisms may be responsible for the explosive battery effects apart from overheating due to the analogy between dendrites formed inside Li-ion batteries and curved wires.

By the previous analysis, it becomes evident that the curvature effect results in a kind of amplification of the free electron concentration. The resulting lowering of the energy eigenvalue is also suggestive of the fact that lower external energy source can now more easily excite this particular mode. However, we cannot actually know how large a part of the externally supplied energy will be effectively coupled to this particular degree of freedom on a realistic macroscopic long thin conductor given the extreme out-of-equi- librium conditions of the high power pulses used here.

The main assumption to be further tested with subsequent experimentation is that given the curvature induced lowering of the eigen-energy for the fundamental state and the concentration of the free electron density near the center, even low energy excitations with very high power can cause the appearance of huge electrical voltages of purely Coulombic nature near the points of maximal concentration due to the rapid removal of the previous electrostatic equilibrium and the extreme polarization induced. Similar effects should be anticipated in the case of thin long metallic stripes of any shape, at least in the case of a curvature present along one of the Euclidean axis only.

We anticipate that the same mechanism could be replicated in some controllable manner in the future to reproduce low energy nuclear reactions and transmutations where the strongly repelled electrons by the free concentrated electrons of the wire are colliding statistically with naked atomic nuclei of atoms of the metallic lattice. We notice here that similar fission phenomena are appearing in the so called Coulombic fission, where strong Coulombic electric fields are caused with various technological apparatus and are used for Stark effect exploitation, the more common of which are referred in existing literature as “Coulomb Explosions” [16] [17] .

In the event that any of the above phenomena like the ones reported here, could be proven useful for energy production, one would want to minimize the input energy expenditures and maximize any possible gains. From this simple argument, we are led to search in an area quite opposite to that utilized in other modern era devices like high energy lasers and accelerators.

Cite this paper

Papageorgiou, C.D. and Raptis, T.E. (2016) Battery Explosions and High Current Bursts during Short Circuit Events on Conducting Paths with Curvature. Open Access Library Journal, 3: e3162. http://dx.doi.org/10.4236/oalib.1103162

References

Appendix A

To establish a generic equivalence of the Schrödinger problem or the general Sturm- Liouville problem in one dimension this is valid not only for ODE problems but also for PDE in separable coordinate systems. To this aim, we consider the representation of a lossless transmission line defined along its geometric length x, with V(x) and I(x) its voltage and current values and X(x), Y(x) its “reactance” and “admittance” per length unit respectively. The general PDE representation of such a line is given as

(A1)

From (A1) one gets the equivalent generic Sturm-Liouville form as

(A2)

This the exact same form of the corresponding Schrödinger operator under the identification of the wavefunction y(x) with the current I(x) and the voltage V(x) with the

logarithmic derivative. Considering an infinitesimal length trans-

mission line dl where both admittance and reactance can be taken as constant, the description becomes identical with that of the so called T-quadrupole circuit shown in Figure 7. The respective impedances are then given as

(A3)

In (A3) we identify the local transmission factor as and the input impedance as. For, we can always approximate this with a proper choice of the step Δx as

(A4)

A succession of such T-quadrupoles can be used to approximate a transmission line with continuously varying parameters of reactance and admittance. In any real transmission line, both γ² as well as Y(x) are functions of the excitation frequency ω associated with the energy parameter E. The frequency values for which the whole line becomes tuned so as to achieve maximal power transmission, are the resonant values which stand for the line eigenvalues and the corresponding current values along the line are the line’s eigenfunctions.

From the well known properties of transmission lines, for any such resonant line, the total reactances calculated from the left and right terminals towards any intermediate point must equal each other with opposite signs. Hence, the resonant values of frequencies or energies can be found from the roots of the total function with L_1,2 the total lengths towards any central point as

(A5)

Given the terminal impedances, the left and right totals can be calculated for any E value.

Having found the eigenvalues from the roots of (A5), it is equally possible to extract the exact shape of the eigenfunctions from the current values as follows. From the general theory of the telegrapher’s equation we know that a solution via a transfer matrix can always be written in the form of a dynamical system, where, the voltage-current vector and T_n an array of the form

(A6)

For any initial condition x₀, one obtains any arbitrary point solution of the original dynamical system as. To understand this type of dynamics we can iso-

late the projections of the transfer matrix in its respective SU(2) basis components. One obtains then the representation where σ_i the respective Pauli matrices and, the coefficients as functions of successive lengths given by. This is recognized as a special case of the Euler-Rodriguez representation of 3D rotations with 2 × 2 matrices. In particular, the above dynamics stands for variable angle rotations on the complex impedance V?I plane.

Appendix B: MATLAB^® Codes for Images

Submit or recommend next manuscript to OALib Journal and we will provide best service for you:

Ÿ Publication frequency: Monthly

Ÿ 9 subject areas of science, technology and medicine

Ÿ Fair and rigorous peer-review system

Ÿ Fast publication process

Ÿ Article promotion in various social networking sites (LinkedIn, Facebook, Twitter, etc.)

Ÿ Maximum dissemination of your research work

Submit Your Paper Online: Click Here to Submit

Or Contact service@oalib.com