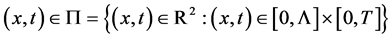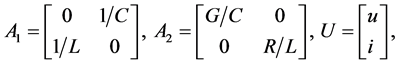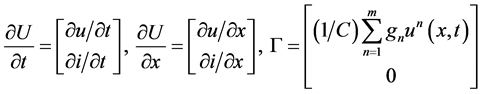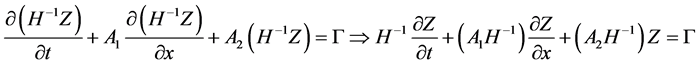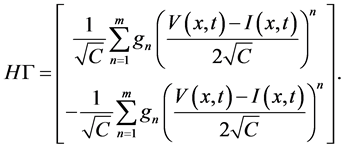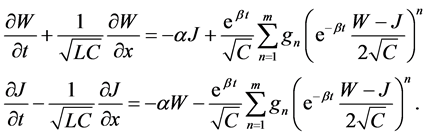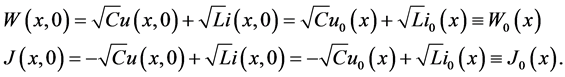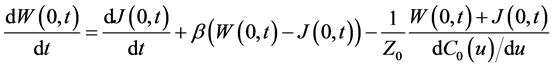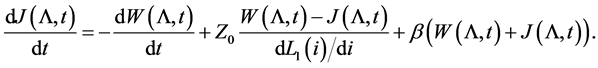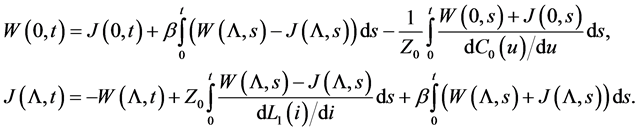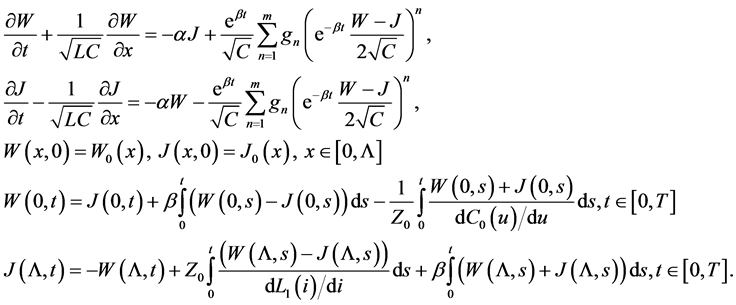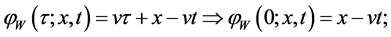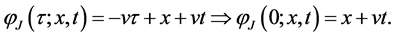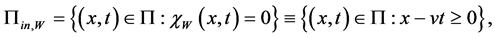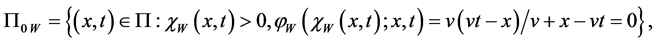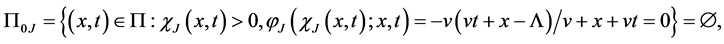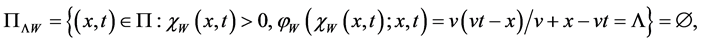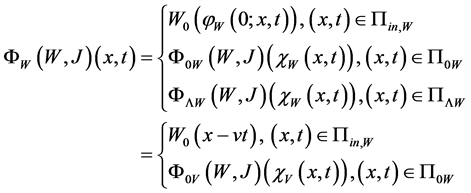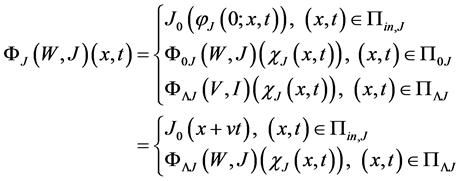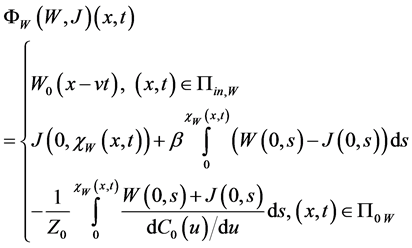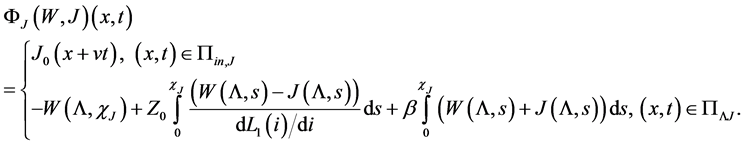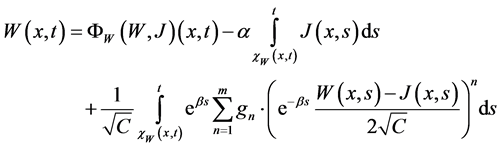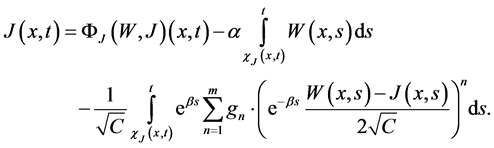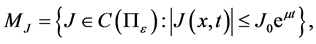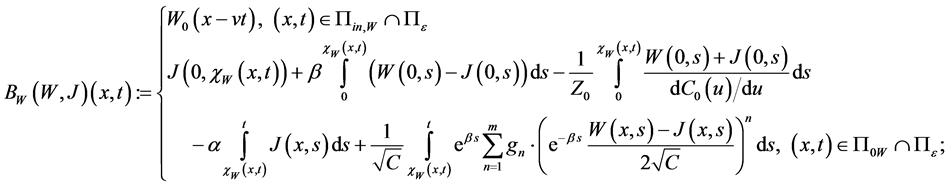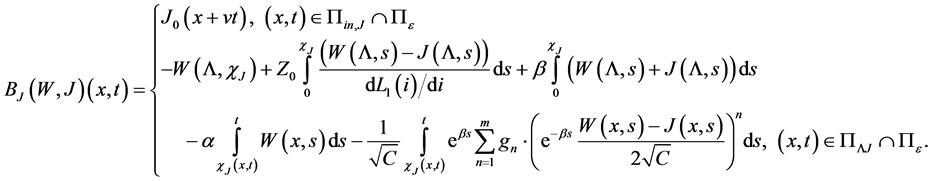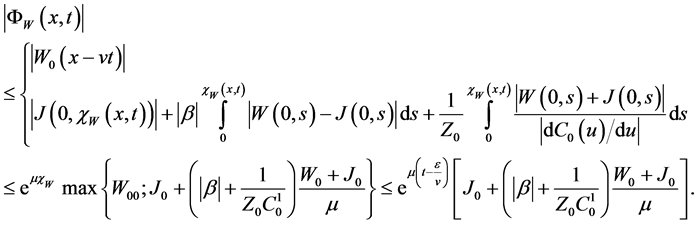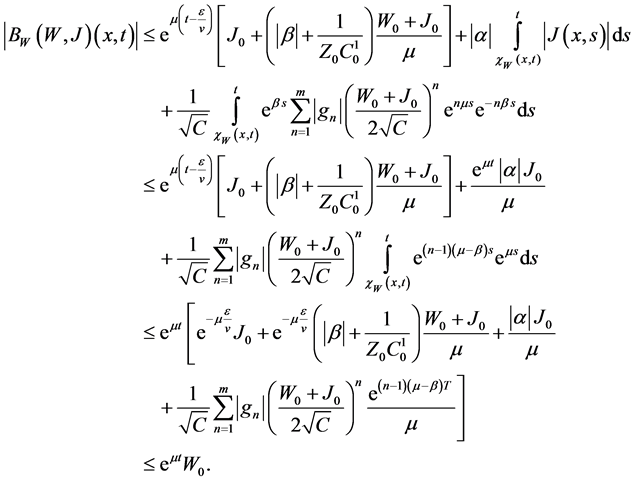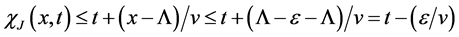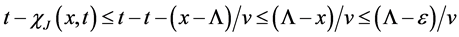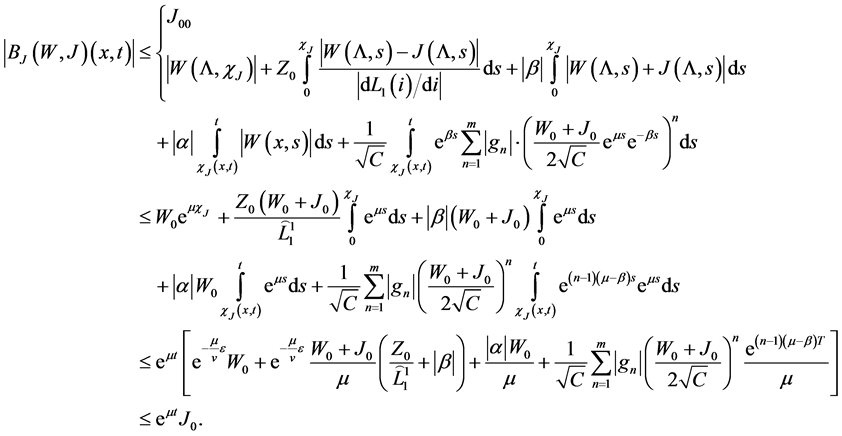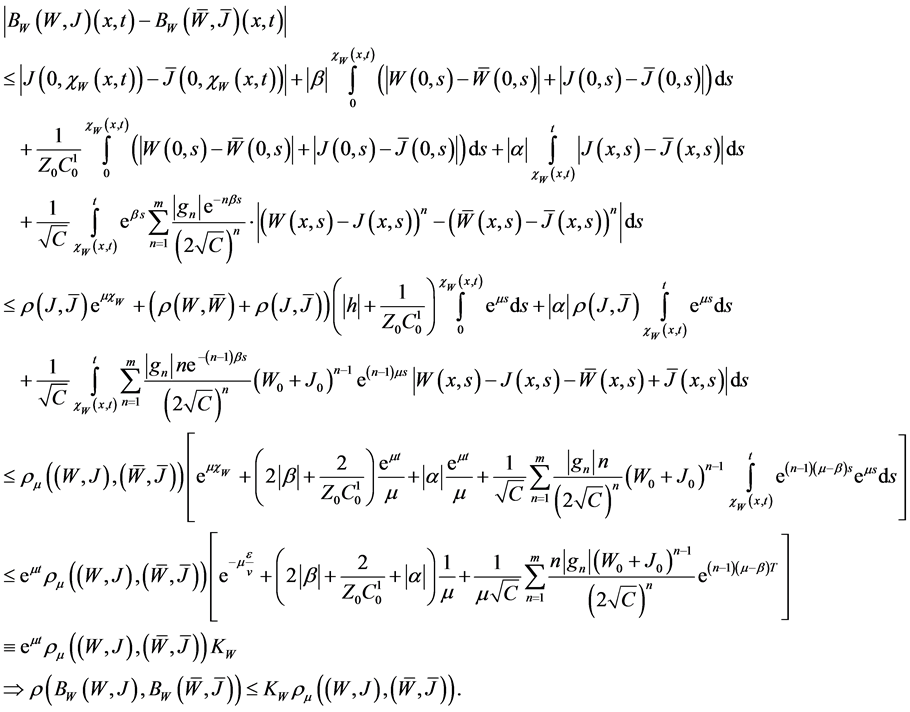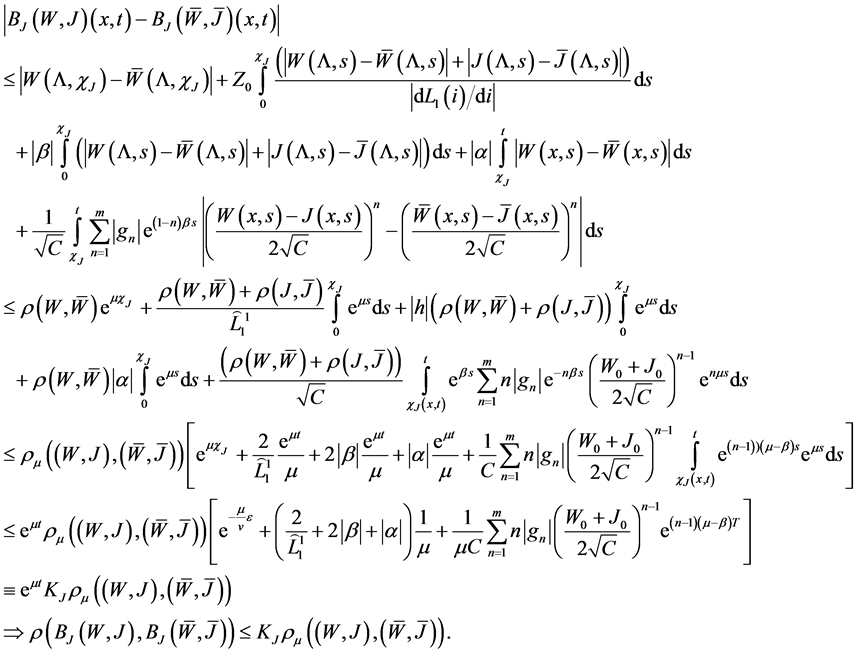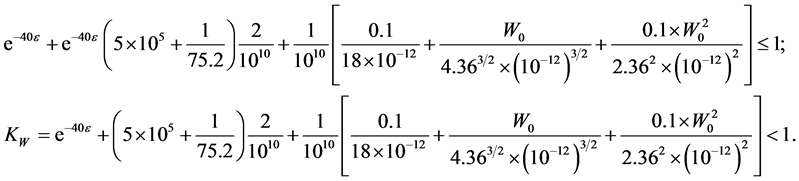Open Access Library Journal
Vol.03 No.11(2016), Article ID:71818,13 pages
10.4236/oalib.1103106
Oscillator with Distributed Nonlinear Structure on a Segment of Lossy Transmission Line
Vasil G. Angelov
Department of Mathematics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria

Copyright © 2016 by author and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 28, 2016; Accepted: November 3, 2016; Published: November 7, 2016
ABSTRACT
We consider a model of self-oscillator with distributed amplifying structure realized on a segment of lossy transmission line. The distributed structure of tunnel diode type generates nonlinearity of polynomial type in the hyperbolic transmission line system. The transmission line is terminated by nonlinear reactive elements at both ends. This means that using Kirchhoff’s law we obtain nonlinear boundary conditions. Then a mixed problem for lossy transmission line system is formulated. We give a new approach to present the mixed problem in a suitable operator form and using fixed point method we prove existence-uniqueness of a solution. To apply the theorem proved one has to check just several inequalities. We demonstrate conditions obtained on a numerical example.
Subject Areas:
Multimedia/Signal Processing
Keywords:
Oscillator Amplifier, Lossy Transmission Line, Nonlinear Distributed Structure, Fixed Point Method

1. Introduction
The present paper is devoted to investigation of self-oscillators with distributed amplifying structure of tunnel diode type realized on a segment of lossy transmission line. The transmission line is terminated by nonlinear reactive elements. Such problems and their applications (for instance to RF-circuits, PCB-s problems and so on) are usually considered by means of various methods (slowly varying in time and space amplitudes and phases, numerical methods and so on, cf. [1] - [14] ). We have developed (cf. [15] ) a general approach for investigation of lossy transmission lines terminated by nonlinear loads without Heaviside condition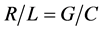 . From mathematical point of view in [15] , we consider just linear hyperbolic systems. In [16] and [17] , we have considered a Josephson superconductive transmission line system with sine type nonlinearities. Our main purpose here is to consider lossy transmission line with polynomial nonlinear distributed structure that leads to a nonlinear hyperbolic system. We extend Abolinya- Myshkis method (cf. reference of [16] ) to attack the nonlinear boundary value problem and propose a new general approach to reduce the mixed problem for such nonlinear systems to an operator form in suitable function spaces. The arising nonlinearity is of polynomial type in view of distributed tunnel diode element. The nonlinear characteristics of the reactive elements generate nonlinear boundary conditions. We prove the existence of an approximated solution of the mixed problem and show a way to reach this solution by successive approximations.
. From mathematical point of view in [15] , we consider just linear hyperbolic systems. In [16] and [17] , we have considered a Josephson superconductive transmission line system with sine type nonlinearities. Our main purpose here is to consider lossy transmission line with polynomial nonlinear distributed structure that leads to a nonlinear hyperbolic system. We extend Abolinya- Myshkis method (cf. reference of [16] ) to attack the nonlinear boundary value problem and propose a new general approach to reduce the mixed problem for such nonlinear systems to an operator form in suitable function spaces. The arising nonlinearity is of polynomial type in view of distributed tunnel diode element. The nonlinear characteristics of the reactive elements generate nonlinear boundary conditions. We prove the existence of an approximated solution of the mixed problem and show a way to reach this solution by successive approximations.
We proceed from the circuit shown on Figure 1, where 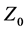 and
and 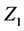 are nonlinear reactive elements. We consider that a particular case
are nonlinear reactive elements. We consider that a particular case  is a nonlinear capacitance, while
is a nonlinear capacitance, while 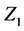 is a nonlinear inductance. In a similar way, it can be treated more complicated circuits (cf. [15] ).
is a nonlinear inductance. In a similar way, it can be treated more complicated circuits (cf. [15] ).
A lossy transmission line with distributed nonlinear resistive element can be prescribed by the following first order nonlinear hyperbolic system of partial differential equations (cf. [1] - [14] ):
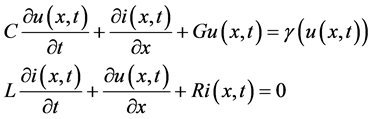 (1)
(1)
where 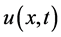 and
and 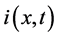 are the unknown voltage and current, while L, C, R and G are inductance, capacitance, resistance and conductance per unit length;
are the unknown voltage and current, while L, C, R and G are inductance, capacitance, resistance and conductance per unit length;  is itslength; and
is itslength; and 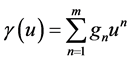 is a prescribed polynomial of arbitrary order with intervalof negative resistance (in the applications most often of third order). For the above
is a prescribed polynomial of arbitrary order with intervalof negative resistance (in the applications most often of third order). For the above
Figure 1. Lossy transmission line with distributed nonlinear resistive element with an interval of negative differential resistance in the characteristic.
system (1), one can formulate the following initial-boundary (or briefly mixed) problem: to find the unknown functions 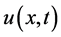 and
and 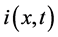 in
in  such that the following initial and boundary conditions are satisfied
such that the following initial and boundary conditions are satisfied
 (2)
(2)
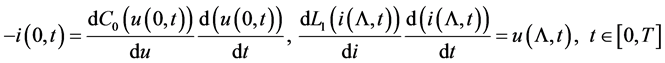 (3)
(3)
where 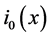 and
and 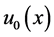
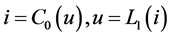
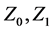
Rewrite the system (1) in the form
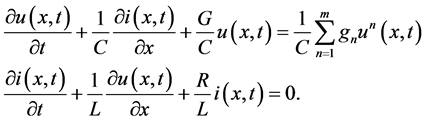
2. Transformation of the Partial Differential System
First we present the system (4) in matrix form:
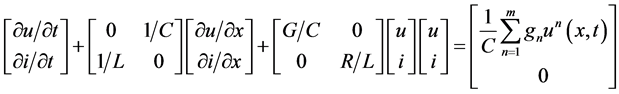
Introducing denotations
we have
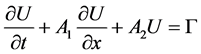
To transform the matrix 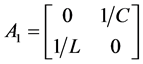


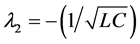

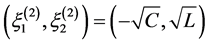
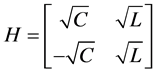
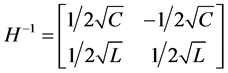
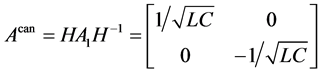
Introduce new variables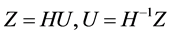
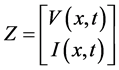
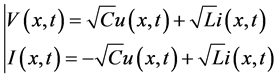
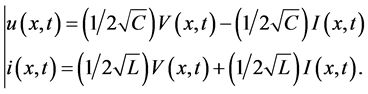
Substituting 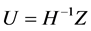
or
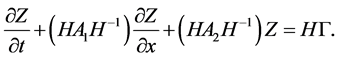
But
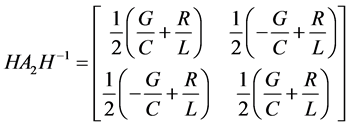
Then introducing denotations 
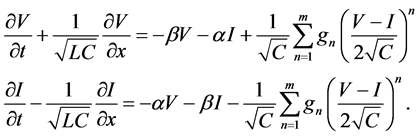
Introduce again new variables
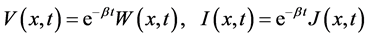
and then the system (8) reduces to
The new transformation formulas are
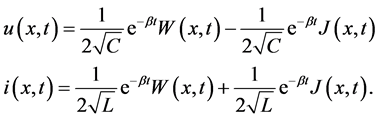
The new initial conditions we obtain from Equations (2), (6) and (9) for
The new boundary conditions we obtain from Equations (3):
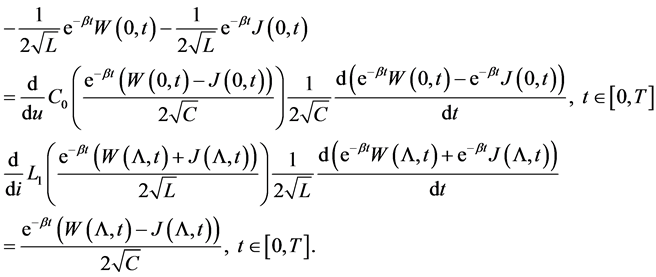
In order to solve the last equations with respect to the derivatives we consider the properties of nonlinear capacitive and inductive elements. For the capacitive element (cf. [15] ) we have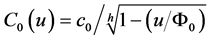
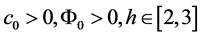
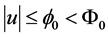
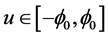
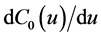
Indeed (cf. [15] ),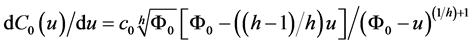
To obtain 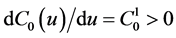
Assumption (C)
If we choose 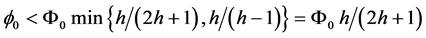
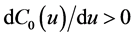
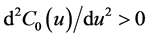
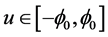
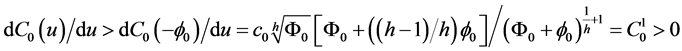
Besides
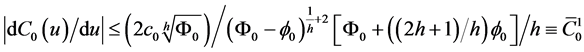
The inductive element has I-L characteristic of polynomial type.
To solve the second equation (11) with respect to 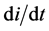
Assumptions (L)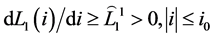
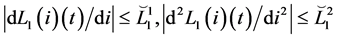
In view of 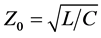
We present the above relations in an integral form under
Assumptions (CC)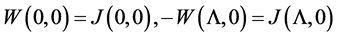
3. Operator Formulation of the Mixed Problem for the Transmission Line System
Now we are able to formulate the mixed problem with respect to the unknown functions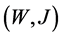
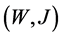
(12)
In what follows we give an operator representation of the above mixed problem (12).
Recall that 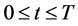

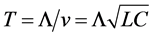
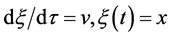
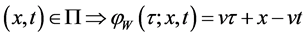
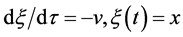
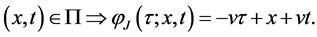
The functions 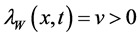
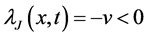
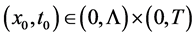
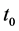
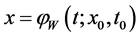
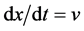
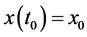
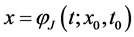
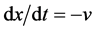
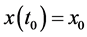
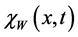
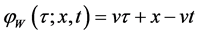
ly the solution 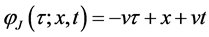
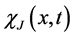
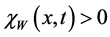
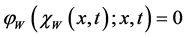
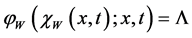
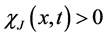
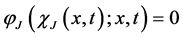
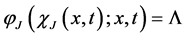
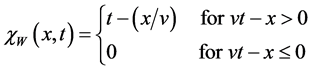
Remark 1. We notice that
Introduce the sets:
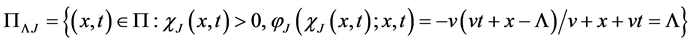
Prior to present problem (12) in operator form we introduce
and
or
So we assign to the above mixed problem the following system of operator equations (cf. [16] , [17] ):
4. Existence Theorem
In order to obtain a contractive operator we consider the mixed problem (12) on the subset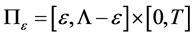
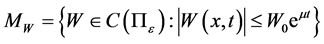
where 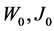
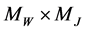
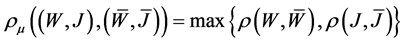
where
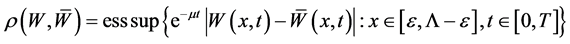
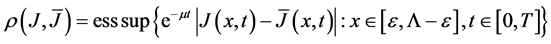
Now we define an operator 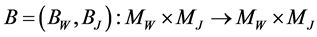
Remark 2. Assumption (C) and Assumptions (L) in view of Equations (10) imply
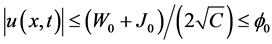
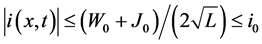
Theorem 1. Let the following conditions be fulfilled:
1) Assumption (C), Assumptions (L), Assumption (CC) and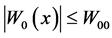
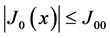

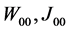
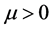
2)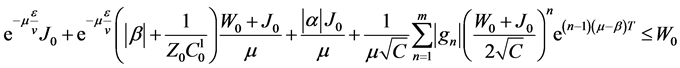
3)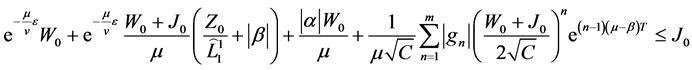
4)
5)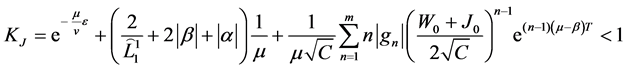
Then there exists a unique solution of the problem (12).
Proof: We establish that the operator B maps the set 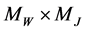
First we notice that 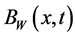
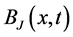
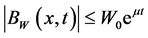
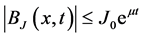
Indeed, for sufficiently small 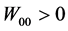
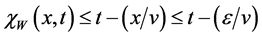
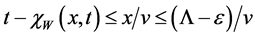
Then for the first component we have
In view of
and
for sufficiently small 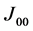
Now we show that B is a contractive operator.
Indeed, for the first component we obtain:
Similarly for the second component we obtain
Therefore
and the operator B has a unique fixed point which is a solution of the mixed problem above formulated in the set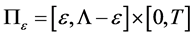
Theorem 1 is thus proved.
Remark 3. We point out that for every 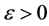
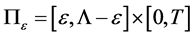
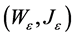
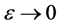
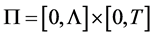
5. Conclusion Remarks
1) We note that the interval 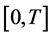
2) We show a simple verification of all inequalities of the main theorem for soft nonlinearity 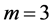
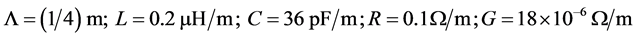
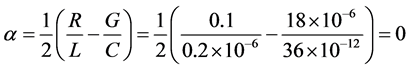
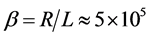
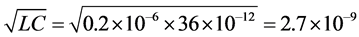
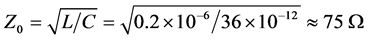
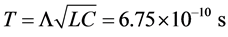
Let us choose a polynomial 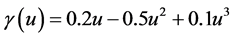
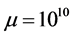
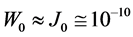
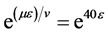
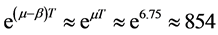
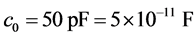
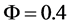
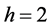
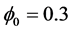
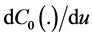
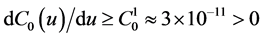
We choose 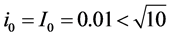
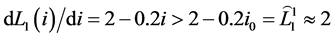
Then the inequalities from Remark 3 and two of inequalities from Theorem 1 become
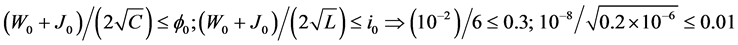
Cite this paper
Angelov, V.G. (2016) Oscillator with Distributed Nonlinear Structure on a Segment of Lossy Transmis- sion Line. Open Access Library Journal, 3: e3106. http://dx.doi.org/10.4236/oalib.1103106
References
- 1. Utkin, G.M. (1978) Auto-Oscillating Systems and Wave Amplifiers. Sovetskoe Radio, Moscow.
- 2. Holt, C. (1967) Introduction in Elec-tromagnetic Fields and Waves. John Wiley & Sons, New York.
- 3. Jordan, E.C. and Balmain, K.G. (1968) Electromagnetic Waves and Radiating Systems. Prentice-Hall, Inc., Englewood Cliffs.
- 4. Ishimaru, A. (1991) Electromagnetic Wave Propagation Radiation and Scattering. Prentice- Hall, Inc., New Jersey.
- 5. Pozar, D. (1998) Microwave Engineering. John Wiley & Sons, New York.
- 6. Paul, C.R. (1994) Analysis of Multi-Conductor Transmission Lines. Wiley-Inter Science Publication, John Wiley & Sons, New York.
- 7. Ramo, S., Whinnery, J.R. and van Duzer, T. (1994) Fields and Waves in Communication Electronics. John Wiley & Sons, Inc., New York.
- 8. Vizmuller, P. (1995) RF Design Guide Systems, Circuits and Equations. Artech House, Inc., Boston, London.
- 9. Magnusson, P.C., Alexander, G.C. and Tripathi, V.K. (1992) Transmission Lines and Wave Propagation. 3rd Edition, CRC Press, Boca Ra-ton.
- 10. Dunlop, J. and Smith, D.G. (1994) Telecommunications Engineering. Chapman & Hall, London.
http://dx.doi.org/10.1007/978-1-4899-2929-7 - 11. Maas, S.A. (2003) Nonlinear Microwave and RF Circuits. 2nd Edition, Artech House, Boston, London.
- 12. Misra, D.K. (2004) Radio-Frequency and Microwave Communication Circuits. Analysis and Design. 2nd Edition, University of Wisconsin-Milwaukee, John Wiley & Sons, Inc., Publication.
http://dx.doi.org/10.1002/0471653764 - 13. Miano, G. and Maffucci, A. (2001) Transmission Lines and Lumped Circuits. Academic Press, New York.
- 14. Scott, A. (1970) Active and Nonlinear Wave Propagation in Electronics. John Wiley & Sons, New York.
- 15. Angelov, V.G. (2014) A Method for Analysis of Transmission Lines Terminated by Nonlinear Loads. Nova Science, New York.
- 16. Angelov, V.G. (2015) Josephson Lossless Transmission Lines with Nonlinear R-Element. International Research Journal of Natural Sciences, 3, 59-79.
- 17. Angelov, V.G. (2016) Lossy Transmission Lines with Josephson Junction—Continuous Generalized Solutions. Communication in Applied Analysis, 20, 91-106.