Applied Mathematics, 2011, 2, 1129-1133
doi:10.4236/am.2011.29156 Published Online September 2011 (http://www.SciRP.org/journal/am)
Reflection of Plane Waves from
a Free S u r f a ce o f a n I ni t i a l l y Stresse d Transversely
Isotropic Dissipative Medium
Baljeet Singh1, Jyoti Arora2
1Department of Mat hem at i cs, Post Graduate Government College, Chandigarh, India
2B.S.A.I.T.M, Alampur, Faridabad, India
Received June 23, 2011; revised July 15, 2011; accepted July 23, 2011
Abstract
The governing equations of a transversely isotropic dissipative medium are solved analytically to obtain the
speeds of plane waves. The appropriate solutions satisfy the required boundary conditions at the stress-free
surface to obtain the expressions of the reflection coefficients of reflected quasi-P (qP) and quasi-SV (qSV)
waves in closed form for the incidence of qP and qSV waves. A particular model is chosen for numerical
computation of these reflection coefficients for a certain range of the angle of incidence. The numerical val-
ues of these reflection coefficients are shown graphically against the angle of incidence for different values
of initial stress parameter. The impact of initial stress parameter on the reflection coefficients is observed
significantly.
Keywords: Transversely Isotropic, Dissipative Medium, Initial Stress, Plane Waves, Reflection, Reflection
Coefficients
1. Introduction
We can not know the Earth completely by assuming
mere an elastic body. If we consider various additional
parameters, e.g. porosity, initial stress, viscosity, dissipa-
tion, temperature, voids, diffusion, etc., then we can un-
derstand better the interior of the Earth. Initial stresses in
a medium are caused by various reasons such as creep,
gravity, external forces, difference in temperatures, etc.
The reflection of plane waves at free surface, interface
and layers is important in estimating the correct arrival
times of plane waves from the source. Various research-
ers studied the reflection and transmission problems at
free surface, interfaces and in layered media [1-12]. The
study of reflection of plane waves in the presence of ini-
tial stresses as well as dissipation is interesting. With the
help of Biot [13] theory of incremental deformation,
Selim [14] studied the reflection of plane waves at a free
surface of an initially stressed dissipative medium. In the
present paper, we studied the problem on reflection of
plane waves at a stress-free surface of an initially stress-
ed transversely isotropic solid half-space with dissipation.
The reflection coefficients of reflected waves are com-
puted numerically to observe the effect of initial stress.
2
. Formulation of the Problem and Solution
Following Biot [13], the basic dynamical equations of
motion in x-z plane for an infinite, initially stressed me-
dium, in the absence of external body forces are,
2
13 11 2
2
31 332
s su
P,
xz zt
ss w
P,
xz xt


  
 
 
  
 
 
(1)
where  is the density, 1w u
2x z
 
 





is rotational
component, sij (i, j = 1, 3) are incremental stress compo-
nents, u and w arethe displacement components.
Following Biot [13], the stress-strainrelations are 
 
11 1113
13 3144333313
uw
sCP CP,
xz
uww u
ssC,sC C
zxzx

 

,

 
 
 


 
(2)
where Cij are the incremental elastic coefficients.

B. SINGH ET AL. 1130
,
,
For dissipative medium, elastic coefficients are re-
placed by the complex constants:
RI RI
111111 131313
RI RI
333333 444444
CCiC,CCiC
CCiC,CCiC
 
 (3)
where, i1,
are real. Following Fung [15], the stress and strain
components in dissipative medium are,
RI RIRIR
111113 13 33 33 44
C,C,C,C,C,C,C,
I
44
C
it it
ij ijii
sse,uue

,

(4)
where (i, j = 1, 3) and  being the angular frequency.
With the help of Equations (3) and (4), the Equation (2)
becomes,



RI RI
11 11 1113 13
RI
31 134444
RI RI
33333313 13
uw
sC iC PC iCP,
xz
uw
ss CiC,
zx
wu
sCiCCiC,
zx



 
 




 

(5)
With the help of Equation (5), the Equation (1) be-
comes,


222
u
RR
R R
1113 4444
22
222
2III I
1113 4444
22
uPwP
CP CCC
2xz 2 xz
uwu
uiCC CC0,
xz xz

 
 

 



 





(6)

22
RRR
331344
2
22
R
44 2
222
IIII
13 444433
22
wPu
CCC
2xz z
Pw
Cw
2x
uww
iC CCC0,
xz xz





 
 
 





 

 







,

n




(7)
The displacement vector is
given by,

(n) nn
u,O,wU
 
n
nn
i
n
Ae

Ud (8)
where (n) assigns an arbitrary direction of propagation of
waves, is the unit displacement vector

nn
13
d,dd
kct

 X
and is the phase factor, in


n
nnn.



 

nn
n
which 13
is the unit propagation vector,
cn is the velocity of propagation = (x, z), and kn is
corresponding wave number, which is related to the an-
gular frequency by
, X
nn
The displacement components un and wn are written
kc .
as
(9)
Making use of Equation (9) into the Equations (6) and
(7

nn
n1 3n
n nikxzc t
n1
n nn3
Ad ue,
Ad w




 



 
), we obtain a system of two homogeneous equations,
which as non-trivial solution if


2
22

nnn
ccIP  0,

 (10)
where,
2
12n 132
ID D,PDD D,









22
22
nn
RR
111 1443
nn
RR
11 1443
P
DCR C
2
iCC ,









RRnnII nn
21344 13134413
P
DCC iCC
2,





 





2
22 2
3
n
RnRn InI
44133 344133 3
D
P
CCiCC
2,







   


  



 

22
nn 22
nn
II4P II4P
c,c
22
 


The roots
co si-P (qP) waves and quasi-SV (qSV) rrespond to qua
waves respectively.
The above two roots give the square of velocities of
propagation as well as damping. Real parts of the right
hand sides correspond to phase velocities and the respec-
tive imginary parts correspond to damping velocities of
qP and qSV waves, respectively. It is observed that both
2
1
c and 2
2
c depend on initial stresses, damping and
ction propagation n dire of

. In the absence of initial
stresses and damping, the ve analysis corresponds to
the case of transversely isotropic elastic solid.
. Reflection of Plane Waves from Fr
abo
3ee
ean initially stressed dissipative half-space
Surface
consider W
occupying the region z > 0 (Figure 1). In this section, we
shall drive the closed form expressions for the reflection
coefficients for incident qP or qSV w ave s.
The displacement components of incident and re-
flected waves are as,


4
j


jj
4
ii
j1 j3
j1 j1
ux,z,tAde,wx,z,t Ade,
j





(11)
where,

B. SINGH ET AL.1131
Figure 1. Geometry of the problem.



(12)
Here, subscripts 1, 2, 3 and 4 correspond to incident
qP
nt and stress compo-
ne




1111 1
2222 2
3333 3
4444 4
kctsinexcosez,
kct sinexcosez,
kct sinexcosez,
kct sinexcosez,

 

  


 


 

wave, incident qSV wave, reflected qP wave and
reflected qSV wave, respecti vely.
In the x-z plane, the displaceme
nts due to the incident qP wave
(
 
11
11 ritten as
,
3

1
1
sin e,cose ) are w

1
1i
11
de,

 
1
11
i
13
uA
wAde


 
1
111
i
131411131
siAQkdcosedsinee





(13)
where,
.
In the x-z plane, the displacement and stress compo-
ne itten as
,
 

1
111
i
33113312 11
siAkQdcoseQdsinee


RI RR
11111213 13
RI RI
333 3344444
QCiC,QC iC,
QCiC,QC iC
 

nts due to the incident qSV wave
(
 
22
12 2
sin e,cose ) are wr

2
2i
de,

3

2
uA
 
2
21
22
i
23
wA de


 
2
222
i
132421232
siAQk[dcosedsine]e


 

2
222
i
33223 32212
siAkQdcoseQdsinee

 (14)
In the x-z plane, the displacement and stress com
ne ritten as
,
,
(15)
In the x-z plane, the displacement and stress compo-
nents due to the reflected qSV wave
4
are written as
,
po-
nts due to the reflected qP wave
(
 
33
13 3
sin e,cose ) are w

3
3i
de,

3

3
 
3
31
33
i
33
uA
wAde



 
3
333
i
133431333
siAQkdcosedsinee


 

 
3
333
i
33333 33213
siAkQdcoseQdsinee,


 

(
 
44
143
sin e,cose)
 
 
4
4
44i
41
44
i
43
uAde,
de



wA
 
4
444
i
134441434
siAQkdcosedsinee


 

 


4
444
i
33443 342 14
siAkQdcoseQdsinee

 , (16)
The boundary conditions requ ired to be satisfied at the
free surface z = 0,
,
 
nn
z33
fs eP0
fs 0,

x1 3 13
n

 
  (17)
The above boundary cond itions are written as
 
1234 123
13 13131313131313
1234
ssssP(e ee
 
4
e)0,
  
33 33 33 33
ssss 0,

 
 (18)
The Equations (11) to (16) will satisfy the boundary
conditions (18), if the following Snell, s law holds
3 12 4
sine sinesinesine
A11 + A22 + A33 + A4
37 + A48 = 0, (21)
where
1234
,
cccc
 (19)
and the following relations hold
4 = 0, (20)
A15 + A26 + A
 

 1113 1
kL dcosedsine,
 

 

 

 

 

 


11
1
22
22123 2
33
331 333
44
443414
11
51331211
22
6233221 2
33
73333213
4
842143
kLd cosed sine,
kLd cosed sine,
kLd sined cose,
kQdcose Qdsine,
kQdcose Qdsine,
kQdcose Qdsine,
kQdsine Qd

 
 
 
 
 
 
 


4
34
cose ,
(22)
and 4P LQ 2



B. SINGH ET AL. 1132
1) For incident qP wave (A2 = 0),
3 45183517 4
13847 13847
AA
,
AA
  

  
, (23)
2) For incident qSV waves (A1 = 0),
34628 362 4
238472 384
AA
,
AA
  

  
7
7
. (24)
For isotropic case, C11 =  + 2  + P, C13=  P = –S11,
then, the above theoretical derivations reduce to Selim
[14].
4. Numerical Example
For numerical purpose, a particular example of the mate-
rial is chosen with the followin g physical constants,
2
From Equations (23) and (24), the reflection
cients of reflected qP and qSV waves are computed for
th
own graphically in Figure 2 for incident qP wave
and in Figure 3 for incident qSV wave.
coefficient of reflected qP
ge of the angle of inci-
r P
= 1 and P = 2 also change at each angle of incidence as
shown by solid line with asters and solid lines with trian-
gles, respectively. The comparison of the variations of
reflection coefficients for P = 0, P = 1 and P = 2, show
the significant effect of initial stress on reflected qP wa
for incident qP wave. Similarly, reflected qSV is also
affected significantly due to the presence of initial stress
as show
R1
C02R10
11 33
102
13 44
I 102I102
11 33
I 102I102
13 44
2.62810N m,C1.56210N m,
0.38510N m,
C1.02510 Nm,C0.95010 N
C0.425 10Nm,C0.325 10Nm,



 
 
 
  
R102R
C0.50810N m,C

  
33
7.14 10 kg m.


 
m ,


coeffi-
e incident qP and qSV waves. The numerical values of
the reflection coefficients of reflected qP and qSV waves
are sh
For P = 0, the reflection
ave oscillates for the whole ranw
dence of qP wave as shown by solid line in Figure 2.
The variations of reflection coefficients of qP wave fo
s
ve
n in Figure 2.
For incident qSV wave, the reflection coefficient of
reflected qP wave first increases to its maximum value
and then decreases to its minimum value at angle e2 =
45˚ when P = 0. Thereafter, it oscillates as shown by
solid line in Figure 3. The variations of reflection coef-
ficients of qP wave for P = 1 and P = 2 are similar to that
for P = 0. The comparison of solid line, solid line with
asters and solid line with triangles shows the significant
effect of initial stress on reflected qP wave for incident
qSV wave. Similarly, reflected qSV is also affected sig-
nificantly due to the presence of initial stress as sh own in
Figure 3.
Figure 2. Variation of the reflection coefficients of qP an
qSV waves against the angle of incidence for incidence of
qP wave.
5. Conclusions
The reflection from the stress-free surface of a trans-
versely isotropic dissipative medium is considered. The
expressions for the reflection coefficients of reflected qP
and qSV waves are obtained in closed form for the inci-
dence of qP and qSV waves. For a particular material,
these coefficients are computed and depicted graphically
against the angle of incidence for different values of ini-
tial stress parameter. From the figures, it observed that 1)
the initial stresses affect significantly the reflection coef-
ficients of all reflected waves. 2) For incident qP wave,
the critical angle for reflected qSV wave is observed at e1
= 45˚ and for incident qSV wave, the critical angle f
d
or
reflected qP wave is observed also at e2 = 45˚. 3) The
effect of initial stresses on the reflection coefficients is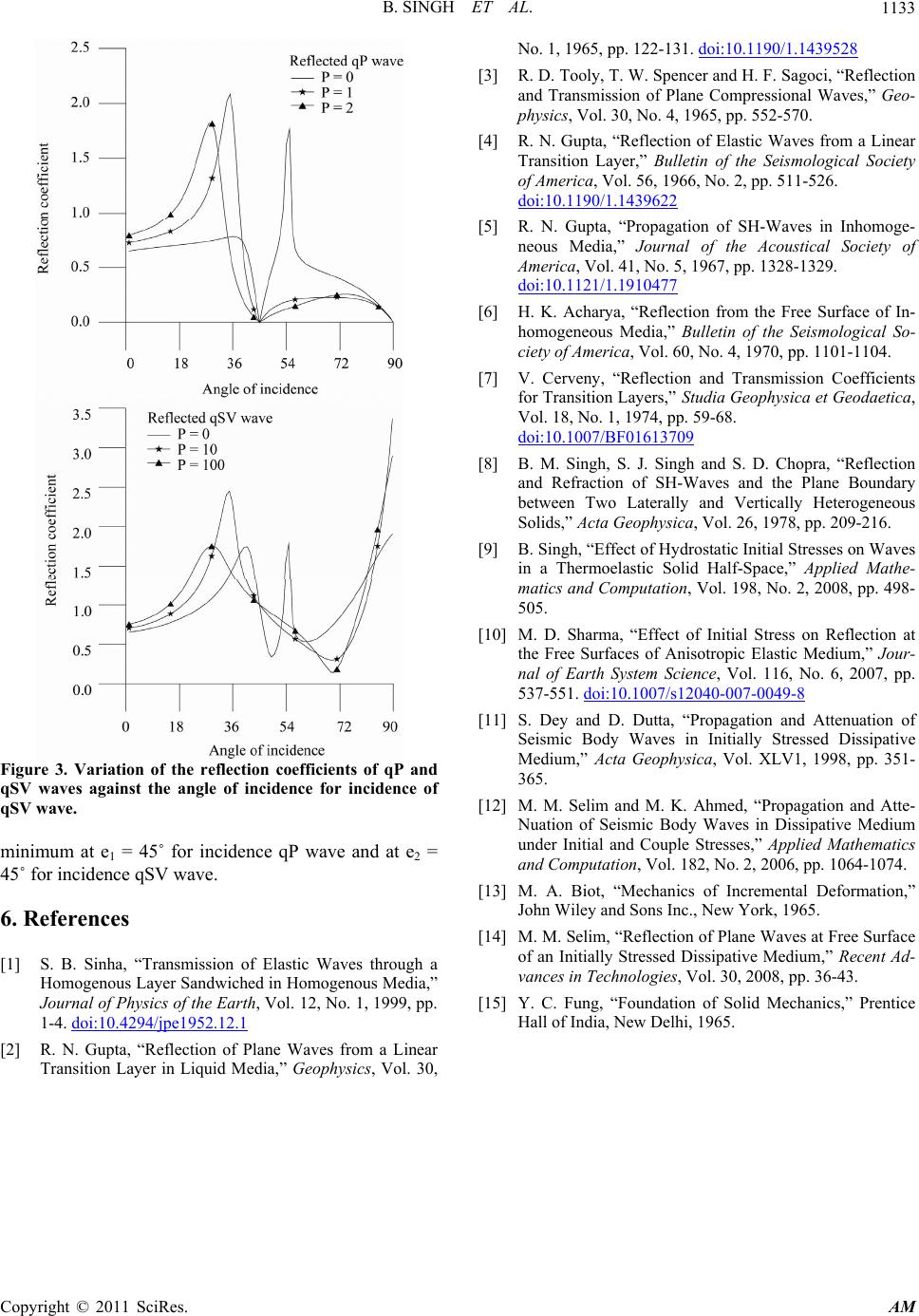

B. SINGH ET AL. 1133
Figure 3. Variation of the reflection coefficients of qP and
qSV waves against the angle of incidence for incidence of
qSV wave.
minimum at e1 = 45˚ for incidence qP wave and at e2 =
45˚ for incidence qSV wave.
6. References
[1] S. B. Sinha, “Transmission of Elastic Waves through a
Homogenous Layer Sandwiched in Homogenous Media,
Journal of Physics of the Earth, Vol. 12, No. 1, 1999, pp.
1-4. doi:10.4294/jpe1952.12.1
”
[2] R. N. Gupta, “Reflection of Plane Waves from a Linear
Transition Layer in Liquid Media,” Geophysics, Vol.
No. 1, 1965, pp. 122-131. doi:10.1190/1.1439528
Compressional Waves,” Geo-
physics, Vol. 30, No. 4, 1965, pp. 552-570.
Reflection of Elastic Waves from a Linear
Transition Layer,” Bulletin of the Seismological Society
[3] R. D. Tooly, T. W. Spencer and H. F. Sagoci, “Reflection
and Transmission of Plane
[4] R. N. Gupta, “
of America, Vol. 56, 1966, No. 2, pp. 511-526.
doi:10.1190/1.1439622
[5] R. N. Gupta, “Propagation of SH-Waves in Inhomoge-
neous Media,” Journal of the Acoustical Society of
America, Vol. 41, No. 5, 1967, pp. 1328-1329.
doi:10.1121/1.1910477
[6] H. K. Acharya, “Reflection from the Free Surface of In-
Coefficients
homogeneous Media,” Bulletin of the Seismological So-
ciety of America, Vol. 60, No. 4, 1970, pp. 1101-1104.
[7] V. Cerveny, “Reflection and Transmission
for Transition Layers,” Studia Geophysica et Geodaetica,
Vol. 18, No. 1, 1974, pp. 59-68.
doi:10.1007/BF01613709
[8] B. M. Singh, S. J. Singh and S. D. Chopra, “Reflection
atic Initial Stresses on Waves
7-0049-8
and Refraction of SH-Waves and the Plane Boundary
between Two Laterally and Vertically Heterogeneous
Solids,” Acta Geophysica, Vol. 26, 1978, pp. 209-216.
[9] B. Singh, “Effect of Hydrost
in a Thermoelastic Solid Half-Space,” Applied Mathe-
matics and Computation, Vol. 198, No. 2, 2008, pp. 498-
505.
[10] M. D. Sharma, “Effect of Initial Stress on Reflection at
the Free Surfaces of Anisotropic Elastic Medium,” Jour-
nal of Earth System Science, Vol. 116, No. 6, 2007, pp.
537-551. doi:10.1007/s12040-00
30,
,” Recent Ad-
[11] S. Dey and D. Dutta, “Propagation and Attenuation of
Seismic Body Waves in Initially Stressed Dissipative
Medium,” Acta Geophysica, Vol. XLV1, 1998, pp. 351-
365.
[12] M. M. Selim and M. K. Ahmed, “Propagation and Atte-
Nuation of Seismic Body Waves in Dissipative Medium
under Initial and Couple Stresses,” Applied Mathematics
and Computation, Vol. 182, No. 2, 2006, pp. 1064-1074.
[13] M. A. Biot, “Mechanics of Incremental Deformation,”
John Wiley and Sons Inc., New York, 1965.
[14] M. M. Selim, “Reflection of Plane Waves at Free Surface
of an Initially Stressed Dissipative Medium
vances in Technologie s, Vol. 30, 2008, pp. 36-43.
[15] Y. C. Fung, “Foundation of Solid Mechanics,” Prentice
Hall of India, New Delhi, 1965.