Applied Mathematics, 2011, 2, 1059-1067
doi:10.4236/am.2011.29147 Published Online September 2011 (http://www.SciRP.org/journal/am)
Numerical Solutions of a Class of Second Order Boundary
Value Problems on Using Bernoulli Polynomials
Md. Shafiqul Islam1*, Afroza Shirin2
1Department of Mathematics, Dhaka University, Dhaka, Bangladesh
2Department of Mathematics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
Received January 24, 2011; revised June 3, 2011; accepted June 10, 2011
Abstract
The aim of this paper is to find the numerical solutions of the second order linear and nonlinear differential
equations with Dirichlet, Neumann and Robin boundary conditions. We use the Bernoulli polynomials as
linear combination to the approximate solutions of 2nd order boundary value problems. Here the Bernoulli
polynomials over the interval [0, 1] are chosen as trial functions so that care has been taken to satisfy the cor-
responding homogeneous form of the Dirichlet boundary conditions in the Galerkin weighted residual
method. In addition to that the given differential equation over arbitrary finite domain [a, b] and the bound-
ary conditions are converted into its equivalent form over the interval [0, 1]. All the formulas are verified by
considering numerical examples. The approximate solutions are compared with the exact solutions, and also
with the solutions of the existing methods. A reliable good accuracy is obtained in all cases.
Keywords: Galerkin Method, Linear and Nonlinear BVP, Bernoulli Polynomials
1. Introduction
There are many linear and nonlinear problems in science
and engineering, namely second order differential equa-
tions with various types of boundary conditions, are
solved either analytically or numerically. In the literature
of numerical analysis solving a two point second order
boundary value problem (BVP) of differential equations,
many authors have attempted to obtain higher accuracy
rapidly by using a numerous methods. Among various
numerical techniques, finite difference method has been
widely used but it takes more computational costs to get
high accuracy. In this method, a large number of pa-
rameters are required and it can not be used to evaluate
the value of the desired points between two grid points.
For this, Galerkin weighted residual method is widely
used to find the approximate results to any point in the
domain of the problem.
Since piecewise polynomials can be differentiated and
integrated easily, and can be approximated any function
to any accuracy desired [1], spline functions have been
studied extensively in [2-9]. Solving BVP only with
Dirichlet boundary conditions has been attempted in [4]
while Bernstein polynomials [10,11] have been used to
solve the two point BVP very recently by the authors
Bhatti and Bracken [1] rigorously by the Galerkin
method. But it is limited only to second order BVP with
Dirichlet boundary conditions, and to first order nonlin-
ear differential equation. On the other hand, Ramadan et
al. [2] has studied linear BVP with Neumann boundary
conditions using quadratic and cubic polynomial splines,
and nonpolynomial splines. We have also found that the
linear BVP with Robin (mixed) boundary conditions
have been solved using finite difference method [12] and
Sinc-Collocation method [13], respectively. Thus except
[9], little attention has been given to solve the second
order nonlinear BVP with Dirichlet and Neumann as
well as Robin boundary conditions. Therefore, the pur-
pose of this paper is to present the Galerkin weighted
residual method to solve both linear and nonlinear sec-
ond order BVP with all types of boundary conditions as
well.
Besides spline functions and Bernstein polynomials,
there is another type of piecewise continuous polynomi-
als, namely Bernoulli polynomials, has been introduced
by Atkinson in [14]. But none has attempted, to the
knowledge of the present authors, using these polynomi-
als to solve the second order BVP. Thus we concentrate
in this paper rigorously to solve some linear and nonlin-
ear BVP with various types of boundary conditions nu-

MD. S. ISLAM ET AL. 1060
k
1
merically, though it is originated in [1].
However, in this paper, we first give an introduction of
Bernoulli polynomials, and then we formulate the Galer-
kin approximation method using Bernoulli polynomials.
We derive the individual formulas for each BVP con-
sisting of Dirichlet, Neumann and Robin boundary con-
ditions, respectively. Numerical examples, for both linear
and nonlinear boundary value problems, are considered
to verify the effectiveness of the derived formulas, and
are also compared with the exact solutions. All the com-
putations are performed by MATHEMATI CA.
2. Bernoulli Polynomials
The Bernoulli polynomials [14, p. 284] of degree
can be defined over the interval [0, 1] implicitly by
n

0
nnk
n
k
n
Brxb x
k





 (1a)
where, are Bernoulli numbers given by
k
b
01b and . (1b)

1
0
d
kk
bBrxxk 

Also Equation (1) can be written explicitly as


  

0
00
00
1
11
1
11,
1
mn
k
m
nk
mn
km
nk
Br x
n
Brxx k
k
n
nkm
k
n












 1
m

(2)
The first 11 Bernoulli polynomials are given bellow:

01Br x


34
5
5
55
63 2
xx x
Br xx 

1
Br xx


24
56
6
53
22
xx
Br xxx

2
2
Br xxx 

356
7
7
777
6622
xx x x
Br xx  

2
3
3
3
22
xx
Br xx 

24 6
78
8
27144
33 3
xx x
Br xxx

23
42Br xxxx 

58
37
9
321 9
26
10 52
xxx
Br xxxx9

 

28
46 9
10
315
57 5
22
xx
Br xxxxx 10
Since Bernoulli polynomials have special properties at
0x

and 1x

:


00Br ,
n

, and 1n


Br 10,
n

2n respectively, so that they can be used
as a set of basis functions to satisfy the corresponding
homogeneous form of the Dirichlet boundary conditions
to derive the matrix formulation of second order BVP
over the interval [0,1].
3. Formulation of Second Order BVP
We consider the general second order linear BVP [15]:
  
dd ,
dd
u
pxqxu rx
xx



 (3a) ,axb




01
',uau ac 
1

 , (3b)
 
01
'ubu bc  2 
where




,px qx and


rx are specified continuous
functions, and 0

, 1

, 0

, 1

, 1, 2 are specified
numbers. Since our aim is to use the Bernoulli polyno-
mials as trial functions which are derived over the inter-
val [0,1], so the BVP (3) is to be converted to an equiva-
lent problem on [0,1] by replacing
c c
x
by


xaba

, and thus we have:
 
dd ,0 1
dd

u
pxqxu rxx
xx


 

  (4a)
 
11
010
0'0,1'1uucuu
ba ba


2
c



 (4b)
where,
   
   
  
2
1,
,



pxp b axa
ba
qxqb axa
rxr b ax a





(4c)
Using Bernoulli polynomials, in Equation (2),
we assume an approximate solution in a form,

i
Br x
 
0
,

n
ii
i
uxaBr x

 (5) 1,n
Now the weighted residual equations corresponding to
the differential Equation (4a) given by
 
1
0
dd d0
dd
1,2, 3,,



j
u
pxqxu rxBr xx
xx
jn

 ,

 
 



 (6)
4
Since from (5), we have

MD. S. ISLAM ET AL.1061

0
00
d d,
dd
00and1


n
i
i
i
n
ii ii
ii
Br ua
xx
ua Brua Br






1
n
After minor simplification, from (6) we can obtain
 
 

 

1
00
0
1
0
1
1
2
1 0
1
1
d
dd
dd
11 1
00 0
11
d
00






























nj
i
ij
i
ij
ij
i
j
j
j
Br
Br
pxqxBr xBrxx
xx
bap BrBr
bap BrBra
cbap Br
rxBr xx
cbapBr
(7)
or, equivalently in matrix form,
,
0
,0,1,2,,
n
ij ij
i
DaF jn


 (8a)
where,

 

1
,
0
0
1
0
1
d
dd
dd
11 1
00 0
,0,1,2,,
j
i
iji j
ij
ij
Br
Br
DpxqxBrxBrx
xx
bapBrBr
bap BrBr
ij n

















x
(8b)
 

 

1
2
1 0
1
1
11
d
00
,
0,1, 2,,
j
jj
j
cbapBr
FrxBrxx
cbapBr
jn











(8c)
Solving the system (8a), we find the values of the pa-
rameters , and then substituting these
parameters in (5), we get the approximate solution of the

0,1,2,,
i
ai n

BVP (4). If we replace x by
x
a
ba


in



ux, then we get
the desired approximate solution of the BVP (3).
The absolute error, of this formulation is defined
by
E
 

Euxux.
Now we discuss the various types of BVP using dif-
ferent boundary conditions as follows:
Case 1: The matrix formulation with the Robin (mixed)
boundary conditions, (i.e., 00

,10,

00,


10


), are already defined in Equations (8).
Case 2: The matrix formulation of the differential
equation (3a) with the Dirichlet boundary conditions (i.e.,
00


, 10,


00,


10

), is given by
,
2
,
n
ij ij
i
DaF


2, 3,,jn (9a)
where,
  
1
,
0
d
dd,
dd
,2,3,,.


j
i
iji j
Br
Br
DpxqxBrxBrx
xx
ij n
x








 (9b)
 
  
1
0
1
0
0
0
d
d
dd,
dd
2,3, ,



jj
j
j
FrxBrxx
Br
pxqxxBrxx
xx
jn








 (9c)
Case 3: The approximate solution of the differential
equation (3a) consisting of Neumann boundary condi-
tions (i.e., 00a

, 10a

, 00,

10,

) can be ob-
tained by putting 00a

and 00,

 in the Equation
(8) as
,
0
,0,1,2,,
n
ij ij
i
DaFj n


 (10a)
where
  
1
,
0
d
dd,
dd
,0,1,2,,


j
i
iji j
Br
Br
Dpx qxBrxBrx
xx
ij n
x








 (10b)
 

1
2
1 0
1
1
11
d
00
,
0,1, 2,,




j
jj
j
cbapBr
FrxBrxx
cb apBr
jn








(10c)
Similar formulation for nonlinear BVP using the Ber-
noulli polynomials can be derived, which will be dis-
cussed through numerical examples in the next section.
4. Numerical Examples
In this section, we explain four linear and two nonlinear
boundary value problems which are available in the ex-
isting literatures, considering three types of boundary
conditions to verify the effectiveness of the present for-

MD. S. ISLAM ET AL. 1062
mulations described in the previous sections. The con-
vergence of each linear BVP is calculated by
 
1nn
Eu xux


,
where denotes the approximate solution by the
proposed method using n-th degree polynomial ap-
proximation. The convergence of nonlinear BVP is as-
sumed when the absolute error of two consecutive itera-
tions is recorded below the convergence criterion

n
ux

such that
1

NN
uu


where is the Newton’s iteration number and
N

varies from .
8
10 
Example 1. First we consider the BVP with Robin
boundary conditions [15]:
2
2
d2cos,π2π
d
uux x
x
  (11a)
 


π23π21,π4π4uu uu

, (11b)
and the exact solution is .

cosux x
The BVP (11) over [0,1] is equivalently to the BVP

2
22
1d ππ
2cos, 01
22
d
π2
uux
x




x (12a)
  
22
0301,141 4
ππ
uu uu

 
(12b)
Using the formula derived in equations (8) and using
different number of Bernoulli polynomials, the approxi-
mate solutions are summarized in Table 1. It is observed
that the accuracy is found nearly the order 69
10, 10


and on using 5, 7 and 9 Bernoulli polynomials,
respectively.
11
10
Example 2. We consider the BVP with Dirichlet
boundary conditions [1]:
2
2
2
de,0 10
d
x
uux x
x

 (13a)
 
00, 100uu (13b)
The exact solution is:
2
10
1e
2
cot10121cos e10
12ecos 2esin
22e
x
xx c
x
xx








x




The BVP (13) is equivalent to the BVP
2
210
2
1d 100e,01
100 d
x
uux x
x

  (14a)


01uu0, (14b)
Using the formula derived in Equations (9), the ap-
proximate solutions, shown in Table 2, are obtained using
8, 10 and 15 Bernoulli polynomials with accuracy up to 3,
4 and 6 significant digits, respectively. It is observed that
using 21 Bernstein polynomials, the accuracy is found
nearly the order of 5
10

in [1].
Example 3. In this case we consider the BVP with
Dirichlet boundary conditions [4]:
2
22
d21
,2 3
d
uu
x xx x

 (15a)


20, 3uu

0

 (15b)
The exact solution is:

2
13
519
38
uxxx6
x







The BVP (15) is equivalent to the BVP

2
22
d2 1
,
2
d2
uux
xx


 01 (16a) ,x


00, 1uu

0

 (16b)
Using the formula derived in Equations (9), the ap-
proximate solutions, shown in Table 3, are obtained on
using 5, 7 and 10 Bernoulli polynomials, and the accuracy
is observed nearly 7, 8 and 9 decimal places, respectively.
On the contrary, the error is obtained nearly 10 10

by
Arshad [10] with 132h

, where

hbaN , a and
b are the endpoints of the domain and N is the number of
subdivision of intervals [a,b].
Example 4. We consider the BVP with Neumann
boundary conditions [2]:
2
2
d1,01
d
uu
xx

 (17a)
 
1cos1 1cos1
0,1
sin1 sin1
uu


 (17b)
whose exact solution is,

1cos1
cossin 1
sin1
ux xx

 
.
Using the formula given in Equations (10), the ap-
proximate solutions, shown in Table 4, are obtained on
using 5, 7 and 10 Bernoulli polynomials with the re-
markable accuracy nearly the order of and
71
10, 10
0
14
10

. On the other hand, Ramadan et al. [6] has found
nearly the accuracy of order 10 , and
66
10

and 8 10

on using quadratic and cubic polynomial splines, and
nonpolynomial spline, respectively with 1128h

,
where


hbaN , a and b are the endpoints of the
domain and N is the number of subdivision of intervals
[a,b].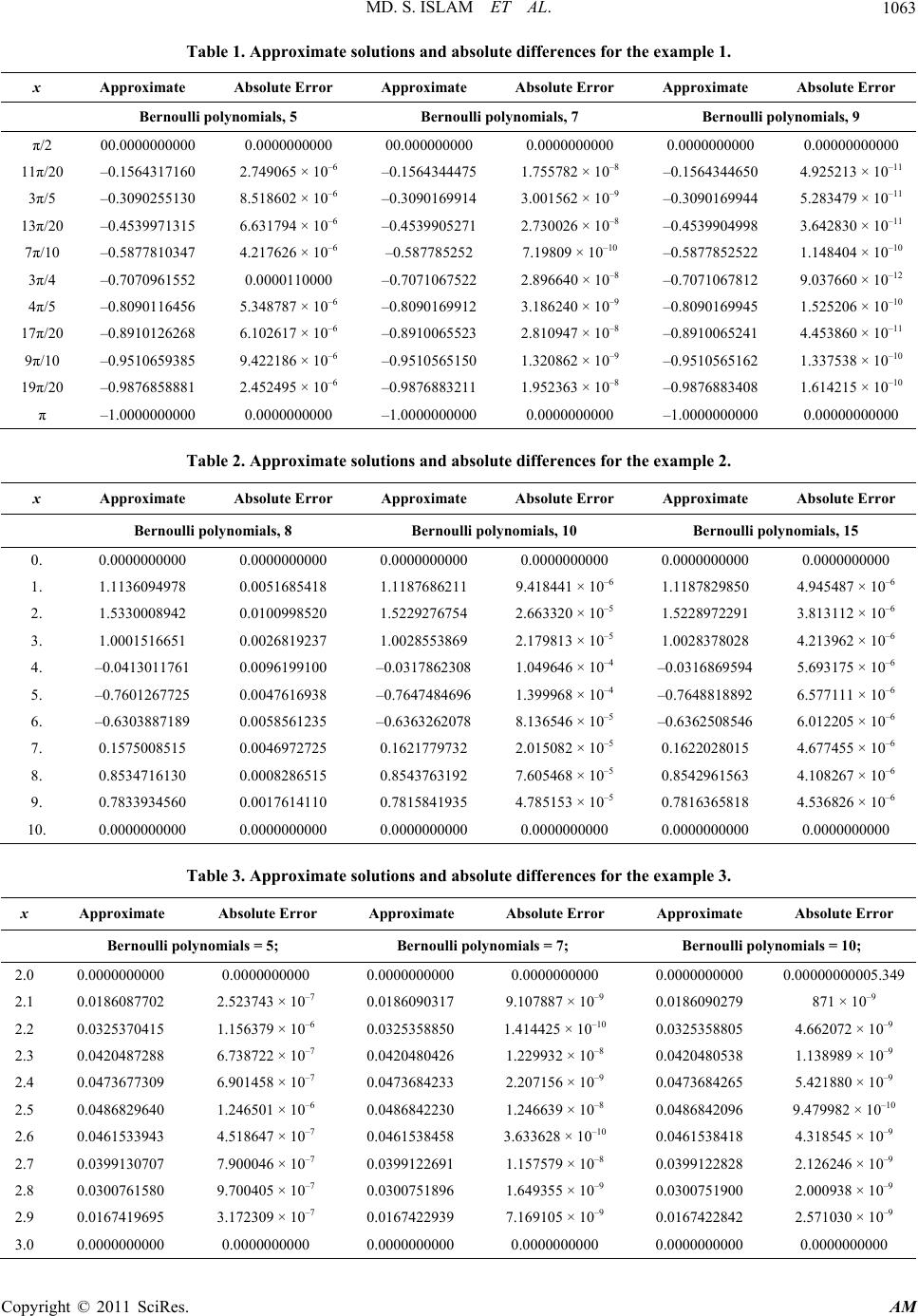

MD. S. ISLAM ET AL. 1063
Table 1. Approximate solutions and absolute differences for the example 1.
x Approximate Absolute Error Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials, 5 Bernoulli polynomials, 7 Bernoulli polynomials, 9
π/2 00.0000000000 0.0000000000 00.000000000 0.0000000000 0.0000000000 0.00000000000
11π/20 –0.1564317160 2.749065 × 10–6 –0.1564344475 1.755782 × 10–8 –0.1564344650 4.925213 × 10–11
3π/5 –0.3090255130 8.518602 × 10–6 –0.3090169914 3.001562 × 10–9 –0.3090169944 5.283479 × 10–11
13π/20 –0.4539971315 6.631794 × 10–6 –0.4539905271 2.730026 × 10–8 –0.4539904998 3.642830 × 10–11
7π/10 –0.5877810347 4.217626 × 10–6 –0.587785252 7.19809 × 10–10 –0.5877852522 1.148404 × 10–10
3π/4 –0.7070961552 0.0000110000 –0.7071067522 2.896640 × 10–8 –0.7071067812 9.037660 × 10–12
4π/5 –0.8090116456 5.348787 × 10–6 –0.8090169912 3.186240 × 10–9 –0.8090169945 1.525206 × 10–10
17π/20 –0.8910126268 6.102617 × 10–6 –0.8910065523 2.810947 × 10–8 –0.8910065241 4.453860 × 10–11
9π/10 –0.9510659385 9.422186 × 10–6 –0.9510565150 1.320862 × 10–9 –0.9510565162 1.337538 × 10–10
19π/20 –0.9876858881 2.452495 × 10–6 –0.9876883211 1.952363 × 10–8 –0.9876883408 1.614215 × 10–10
π –1.0000000000 0.0000000000 –1.0000000000 0.0000000000 –1.0000000000 0.00000000000
Table 2. Approximate solutions and absolute differences for the example 2.
x Approximate Absolute Error Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials, 8 Bernoulli polynomials, 10 Bernoulli polynomials, 15
0. 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
1. 1.1136094978 0.0051685418 1.1187686211 9.418441 × 10–6 1.1187829850 4.945487 × 10–6
2. 1.5330008942 0.0100998520 1.5229276754 2.663320 × 10–5 1.5228972291 3.813112 × 10–6
3. 1.0001516651 0.0026819237 1.0028553869 2.179813 × 10–5 1.0028378028 4.213962 × 10–6
4. –0.0413011761 0.0096199100 –0.0317862308 1.049646 × 10–4 –0.0316869594 5.693175 × 10–6
5. –0.7601267725 0.0047616938 –0.7647484696 1.399968 × 10–4 –0.7648818892 6.577111 × 10–6
6. –0.6303887189 0.0058561235 –0.6363262078 8.136546 × 10–5 –0.6362508546 6.012205 × 10–6
7. 0.1575008515 0.0046972725 0.1621779732 2.015082 × 10–5 0.1622028015 4.677455 × 10–6
8. 0.8534716130 0.0008286515 0.8543763192 7.605468 × 10–5 0.8542961563 4.108267 × 10–6
9. 0.7833934560 0.0017614110 0.7815841935 4.785153 × 10–5 0.7816365818 4.536826 × 10–6
10. 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
Table 3. Approximate solutions and absolute differences for the example 3.
x Approximate Absolute Error Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials = 5; Bernoulli polynomials = 7; Bernoulli polynomials = 10;
2.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.00000000005.349
2.1 0.0186087702 2.523743 × 10–7 0.0186090317 9.107887 × 10–9 0.0186090279 871 × 10–9
2.2 0.0325370415 1.156379 × 10–6 0.0325358850 1.414425 × 10–10 0.0325358805 4.662072 × 10–9
2.3 0.0420487288 6.738722 × 10–7 0.0420480426 1.229932 × 10–8 0.0420480538 1.138989 × 10–9
2.4 0.0473677309 6.901458 × 10–7 0.0473684233 2.207156 × 10–9 0.0473684265 5.421880 × 10–9
2.5 0.0486829640 1.246501 × 10–6 0.0486842230 1.246639 × 10–8 0.0486842096 9.479982 × 10–10
2.6 0.0461533943 4.518647 × 10–7 0.0461538458 3.633628 × 10–10 0.0461538418 4.318545 × 10–9
2.7 0.0399130707 7.900046 × 10–7 0.0399122691 1.157579 × 10–8 0.0399122828 2.126246 × 10–9
2.8 0.0300761580 9.700405 × 10–7 0.0300751896 1.649355 × 10–9 0.0300751900 2.000938 × 10–9
2.9 0.0167419695 3.172309 × 10–7 0.0167422939 7.169105 × 10–9 0.0167422842 2.571030 × 10–9
3.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000

MD. S. ISLAM ET AL. 1064
Table 4. Approximate solutions and absolute differences for the example 4.
x Approximate Absolute Error Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials = 5 Bernoulli polynomial = 7 Bernoulli polynomials = 10
0.0 0.0000000000 1.153937 × 10–10 0.0000000000 0.0000000000 0.0000000000 0.0000000000
0.1 0.0495431439 2.654280 × 10–7 0.0495434086 8.177960 × 10–10 0.0495434094 1.932482 × 10–14
0.2 0.0886011150 9.870426 × 10–7 0.0886001278 8.626597 × 10–11 0.0886001279 2.672862 × 10–14
0.3 0.1167806021 6.883117 × 10–7 0.1167799150 1.222063 × 10–9 0.1167799138 1.992850 × 10–14
0.4 0.1338006690 5.349698 × 10–7 0.1338012039 9.031828 × 10–11 0.1338012040 1.013079 × 10–14
0.5 0.1394927538 1.173569 × 10–6 0.1394939260 1.280755 × 10–9 0.1394939273 2.942091 × 10–14
0.6 0.1338006690 5.349698 × 10–7 0.1338012039 9.031831 × 10–11 0.1338012040 1.010303 × 10–14
0.7 0.1167806021 6.883117 × 10–7 0.1167799150 1.222063 × 10–9 0.1167799138 1.981748 × 10–14
0.8 0.0886011150 9.870426 × 10–7 0.0886001278 8.626594 × 10–11 0.0886001279 2.670086 × 10–14
0.9 0.0495431439 2.654280 × 10–7 0.0495434085 8.177957 × 10–10 0.0495434094 1.942890 × 10–14
1.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
We now also implement the procedure described in
section 3 to find the numerical solutions of two nonlinear
second order boundary value problems.
Example 5. We consider a nonlinear BVP with
Dirichlet boundary conditions [16]
2
3
2
d1d 1
4
8d 4
d
uu
ux
x
x




, (18a) 1x3

117u and

3433u (18b)
The exact solution of the problem is given by

216
ux x
x

To use Bernoulli polynomials, first we convert the
BVP (18) to an equivalent BVP on


0,1 by replacing
x
by 21
x
 such that

23
2
d1d
16 21
4d
d
uu
ux
x
x
, (19a) 0x1,

017u and

143u3. (19b)
Assume that the approximate solution of (19) using
Bernoulli polynomials is given by
 
0
2
,

n
ii
i
uxxaBr x 


 (20) 2,n
where

017 8 3
x
x   is specified by the Dirichlet
boundary conditions at and , and
for each
0x1x
3, ,in
 
01
ii
Br Br02, .
The weighted residual equations of (19a) correspond-
ing to the approximation (20), given by

123
2
0
d1d
1621()d0
4d d
2, 3,,.



k
uu
uxBrx
x x
kn








Exploiting integration by parts with minor simplifica-
tions, we obtain


1
0
0
20
2
1300
0
0
ddd d
1
dd 4dd
d
1d
4d
dd d
1
16 21d
dd 4d
2,3,,
n
iki
kik
i
nj
jik i
j
k
kk
BrBrBrBrBr Br
xxxx
Br
aBrBrxa
x
Br
x
BrBrx
xx x
kn







 















 








(22)
The above Equations (22) are equivalent to the matrix
form


DCAG (23)
where the elements of the matrix ,,
A
CD
and G are
and
,,
,,
iikik
ac dk
g
, respectively, given by
1
0
,0
0
ddd d
1
dd
dd 4dd
ik i
ikki k
BrBrBr BrBr Brx
xxxx





 

 




(24a)
1
,
20
d
1d
4d
nj
ikj ik
j
Br
caBrBr
x




x 
(24b)


1300
0
0
dd d
1
16 21d
dd 4d
k
kk
Br
k
g
xBrBr
xx x

 x


 





(24c)
x




(21)
The initial values of these coefficients i are ob-
tained by applying the Galerkin method to the BVP ne-
glecting the nonlinear term in (19a). That is, to find ini-
tial coefficients, we will solve the system
a
DA G (25a)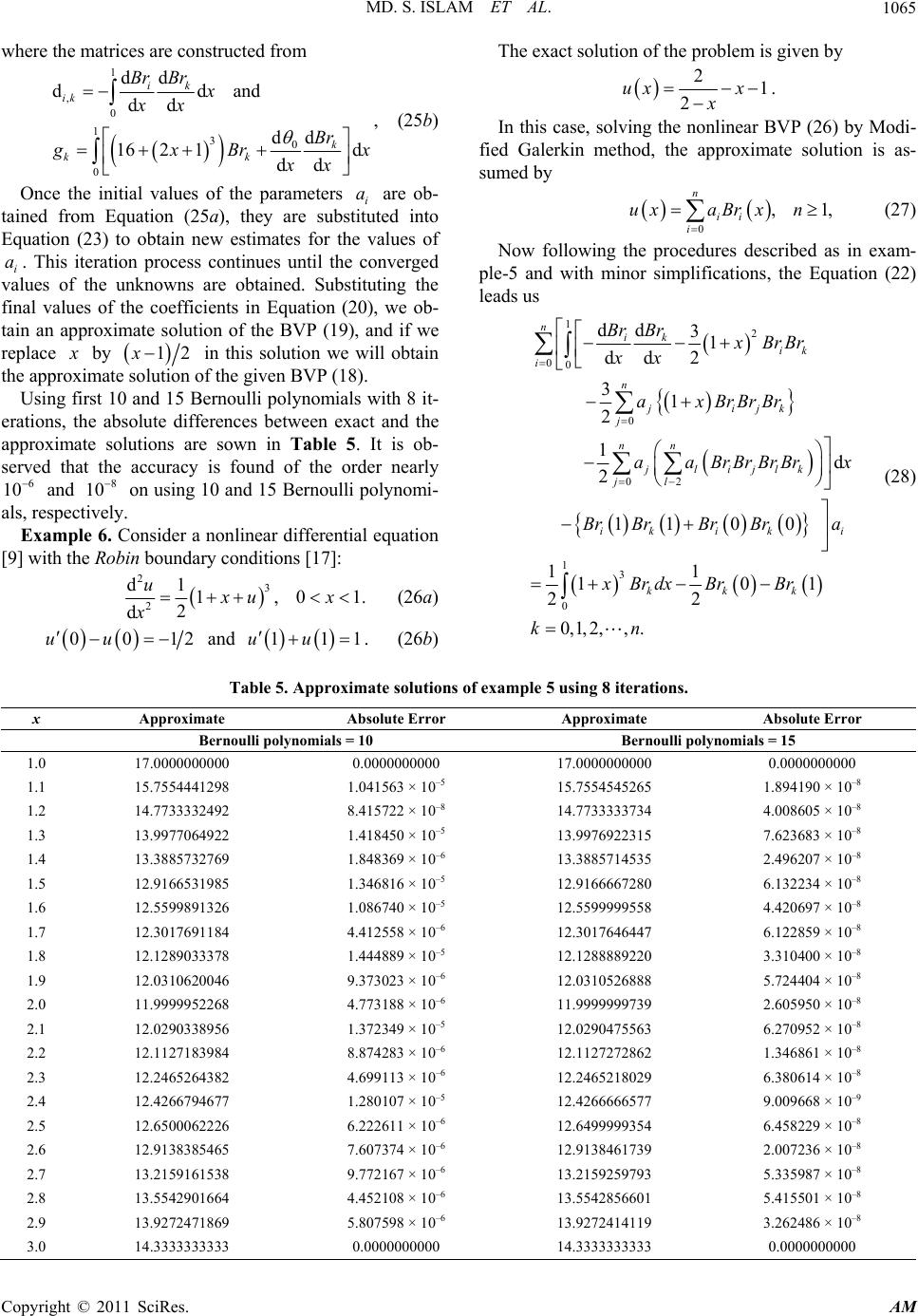

MD. S. ISLAM ET AL.1065
where the matrices are constructed from


1
,
0
130
0
dd
ddand
dd
dd
16 21d
dd
ik
ik
k
kk
Br Brx
xx
Br
g
xBr
xx



 



x


, (25b)
Once the initial values of the parameters i are ob-
tained from Equation (25a), they are substituted into
Equation (23) to obtain new estimates for the values of
i. This iteration process continues until the converged
values of the unknowns are obtained. Substituting the
final values of the coefficients in Equation (20), we ob-
tain an approximate solution of the BVP (19), and if we
replace
a
a
x
by

12x in this solution we will obtain
the approximate solution of the given BVP (18).
Using first 10 and 15 Bernoulli polynomials with 8 it-
erations, the absolute differences between exact and the
approximate solutions are sown in Table 5. It is ob-
served that the accuracy is found of the order nearly
and on using 10 and 15 Bernoulli polynomi-
als, respectively.
6
108 10
Example 6. Consider a nonlinear differential equation
[9] with the Robi n boundary conditions [17]:

23
2
d1
1,
2 d
u
x
u
x (26a) 0x1.
 
001uu 
The exact solution of the problem is given by

21
2
ux x
x


.
In this case, solving the nonlinear BVP (26) by Modi-
fied Galerkin method, the approximate solution is as-
sumed by
 
0
,
n
ii
i
uxaBr x

 (27) 1,n
Now following the procedures described as in exam-
ple-5 and with minor simplifications, the Equation (22)
leads us




  

 
12
00
0
02
13
0
dd 31
dd 2
31
2
1d
2
110 0
11
10
22
0,1, 2,,.















 








n
ik
ik
i
n
jijk
j
nn
jlijlk
jl
ikik
kkk
Br BrxBrBr
xx
axBr BrBr
aaBrBrBrBrx
Br BrBrBra
xBrdx BrBr
kn
1
i
(28)
21 and . (26b)
 
11uu 
Table 5. Approximate solutions of example 5 using 8 iterations.
x Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials = 10 Bernoulli polynomials = 15
1.0 17.0000000000 0.0000000000 17.0000000000 0.0000000000
1.1 15.7554441298 1.041563 × 10–5 15.7554545265 1.894190 × 10–8
1.2 14.7733332492 8.415722 × 10–8 14.7733333734 4.008605 × 10–8
1.3 13.9977064922 1.418450 × 10–5 13.9976922315 7.623683 × 10–8
1.4 13.3885732769 1.848369 × 10–6 13.3885714535 2.496207 × 10–8
1.5 12.9166531985 1.346816 × 10–5 12.9166667280 6.132234 × 10–8
1.6 12.5599891326 1.086740 × 10–5 12.5599999558 4.420697 × 10–8
1.7 12.3017691184 4.412558 × 10–6 12.3017646447 6.122859 × 10–8
1.8 12.1289033378 1.444889 × 10–5 12.1288889220 3.310400 × 10–8
1.9 12.0310620046 9.373023 × 10–6 12.0310526888 5.724404 × 10–8
2.0 11.9999952268 4.773188 × 10–6 11.9999999739 2.605950 × 10–8
2.1 12.0290338956 1.372349 × 10–5 12.0290475563 6.270952 × 10–8
2.2 12.1127183984 8.874283 × 10–6 12.1127272862 1.346861 × 10–8
2.3 12.2465264382 4.699113 × 10–6 12.2465218029 6.380614 × 10–8
2.4 12.4266794677 1.280107 × 10–5 12.4266666577 9.009668 × 10–9
2.5 12.6500062226 6.222611 × 10–6 12.6499999354 6.458229 × 10–8
2.6 12.9138385465 7.607374 × 10–6 12.9138461739 2.007236 × 10–8
2.7 13.2159161538 9.772167 × 10–6 13.2159259793 5.335987 × 10–8
2.8 13.5542901664 4.452108 × 10–6 13.5542856601 5.415501 × 10–8
2.9 13.9272471869 5.807598 × 10–6 13.9272414119 3.262486 × 10–8
3.0 14.3333333333 0.0000000000 14.3333333333 0.0000000000

MD. S. ISLAM ET AL. 1066
Table 6. Approximate solutions of examples using 8 iterations.
x Approximate Absolute Error Approximate Absolute Error
Bernoulli polynomials, 8 Bernoulli polynomials, 10
0.0 00.0000000000 0.0000000000 00.0000000000 0.0000000000
0.1 –0.0473680463 3.747086 × 10–7 –0.0473684172 3.803934 × 10–9
0.2 –0.0888891811 2.922364 × 10–7 –0.0888888959 6.992957 × 10–9
0.3 –0.1235296394 2.276838 × 10–7 –0.1235293980 1.372571 × 10–8
0.4 –0.1499995043 4.957444 × 10–7 –0.1500000116 1.157174 × 10–8
0.5 –0.1666665743 9.237249 × 10–8 –0.1666666693 2.681433 × 10–9
0.6 –0.1714291237 5.522990 × 10–7 –0.1714285563 1.508438 × 10–8
0.7 –0.1615383671 9.448797 × 10–8 –0.1615384751 1.360781 × 10–8
0.8 –0.1333328804 4.528913 × 10–7 –0.1333333287 4.621790 × 10–9
0.9 –0.0818186682 4.863450 × 10–7 –0.0818181840 2.134837 × 10–9
1.0 00.0000000000 0.0000000000 00.0000000000 0.0000000000
which can be written in a matrix form, similar to the sys-
tem (23),

DCBAG (29a)
where the elements of ,,,
A
BCD
k
and G are
and
,, ,
,,,
iikikik
ab cd
g
, respectively, given by

  
12
,
0
dd 3
d1d
dd2
1100
ik
iki K
ikik
Br Br
x
Br Brx
xx
Br BrBrBr





 (29b)
 
1
,
00
31d
2
n
ikjij k
j
caxBrBrBr


x (29c)

1
,
00
0
1d
2
nn
ikjlij lk
jl
baaBrBrBrBr







x



(29d)
 
13
0
11
1d 0
22
kkk
gxBrxBrB 
1
k
r (29e)
To find the initial coefficients, on neglecting the
nonlinear terms as we have done in example 5, we solve
the reduced system
,DA G (30a)
where the elements of and , respectively, are
now
,DA G

  
12
,
0
dd 3
d1
dd2
1100
ik
iki K
ikik
Br Brd
x
Br Brx
xx
Br BrBrBr





 

(30b)
  
13
0
11
10
22
kkk
gxBr dxBrBr 
1 k
(30c)
The results are summarized in the Table 6 that ob-
tained on using 8 and 10 Bernoulli polynomials with 8
iterations at various points of the domain of the problems.
It is observed that the approximate results converge
monotonically to the exact solutions.
5. Conclusions
We have discussed, in details, the formulation of one
dimensional linear and nonlinear second order boundary
value problems by Galerkin weighted residual method,
using Bernoulli polynomials which have been used as the
trial functions in the approximation. Some numerical
examples are tested. All the mathematical formulations
and numerical computations have been evaluated by
MATHEMATICA code. The computed solutions are com-
pared with the exact solutions, and we have found a good
agreement with the exact solution.
6. References
[1] M. I. Bhatti and P. Bracken, “Solutions of Differential
Equations in a Bernstein Polynomial Basis,” Journal of
Computational and Applied Mathematics, Vol. 205, No. 1,
2007, pp. 272-280. doi:10.1016/j.cam.2006.05.002.
[2] M. A. Ramadan, I. F. Lashien and W. K. Zahra, “Poly-
nomial and Nonpolynomial Spline Approaches to the
Numerical Solution of Second Order Boundary Value
Problem,” Applied Mathematics and Computation, Vol.
184, No. 2, 2007, pp. 476-484.
doi:10.1016/j.amc.2006.06.053.
[3] R.A. Usmani and M. Sakai, “A Connection between
Quartic Spline and Numerov Solution of a Boundary
Value Problem,” International Journal of Computer
Mathematics, Vol. 26, No. 3, 1989, pp. 263-273.
doi:10.1080/00207168908803700
[4] Arshad Khan, “Parametric Cubic Spline Solution of Two
Point Boundary Value Problems,” Applied Mathematics
and Computation, Vol. 154, No. 1, 2004, pp. 175-182.
doi:10.1016/S0096-3003(03)00701-X.

MD. S. ISLAM ET AL.1067
[5] E. A. Al-Said, “Cubic Spline Method for Solving Two
Point Boundary Value Problems,” Korean Journal of
Computational and Applied Mathematics, Vol. 5, 1998,
pp. 759-770.
[6] E. A. Al-Said, “Quadratic Spline Solution of Two Point
Boundary Value Problems,” Journal of Natural Geome-
try, Vol. 12, 1997, pp. 125-134.
[7] D. J. Fyfe, “The Use of Cubic Splines in the Solution of
Two Point Boundary Value Problems,” The Computer
Journal, Vol. 12, No. 2, 1969, pp. 188-192.
doi:10.1093/comjnl/12.2.188
[8] A. K. Khalifa and J. C. Eilbeck, “Collocation with Quad-
ratic and Cubic Splines,” The IMA Journal of Numerical
Analysis, Vol. 2, No. 1, 1982, pp. 111-121.
doi:10.1093/imanum/2.1.111
[9] G. Mullenheim, “Solving Two-Point Boundary Value
Problems with Spline Functions,” The IMA Journal of
Numerical Analysis, Vol. 12, No. 4, 1992, pp. 503-518.
doi:10.1093/imanum/12.4.503
[10] J. Reinkenhof, “Differentiation and Integration Using
Bernstein’s Polynomials,” International Journal for Nu-
merical Methods in Engineering, Vol. 11, No. 10, 1977,
pp. 1627-1630. doi:10.1002/nme.1620111012
[11] E. Kreyszig, “Bernstein Polynomials and Numerical In-
tegration,” International Journal for Numerical Methods
in Engineering, Vol. 14, No. 2, 1979, pp. 292-295.
doi:10.1002/nme.1620140213
[12] R. A. Usmani, “Bounds for the Solution of a Second Or-
der Differential Equation with Mixed Boundary Condi-
tions,” Journal of Engineering Mathematics, Vol. 9, No.
2, 1975, pp. 159-164. doi:10.1007/BF01535397
[13] B. Bialecki, “Sinc-Collocation Methods for Two Point
Boundary Value Problems,” The IMA Journal of Nu-
merical Analysis, Vol. 11, No. 3, 1991, pp. 357-375.
doi:10.1093/imanum/11.3.357
[14] K. E. Atkinson, “An Introduction to Numerical Analy-
sis,” 2nd Edition, John Wiley and Sons, New York, 1989,
pp- 284.
[15] P. E. Lewis and J. P. Ward, “The Finite Element Method,
Principles and Applications,” Addison-Wesley, Boston
1991.
[16] R. L. Burden and J. D. Faires, “Numerical Analysis,”
Brooks/Cole Publishing Co., Pacific Grove, 1992.
[17] M. K. Jain, “Numerical Solution of Differential Equa-
tions,” 2nd Edition, New Age International, New Delhi,
2000.