American Journal of Computational Mathematics, 2011, 1, 189-201
doi:10.4236/ajcm.2011.13022 Published Online September 2011 (http://www.SciRP.org/journal/ajcm)
Simulation of Human Phonation with Vocal Nodules
Shinji Deguchi1,2,*, Yuki Kawahara3
1Department of Biomedical Engineering, Tohoku University, Sendai, Japan
2Department of Bioengineering and Robotics, Tohoku University, Sendai, Japan
3Graduate School of Natural Science and Technology, Okayama University, Sendai, Japan
Received June 16, 2011; revised July 20, 2011; accepted August 2, 2011
Abstract
The geometric and biomechanical properties of the larynx strongly influence voice quality and efficiency. A
physical understanding of phonation natures in pathological conditions is important for predictions of how
voice disorders can be treated using therapy and rehabilitation. Here, we present a continuum-based numeri-
cal model of phonation that considers complex fluid-structure interactions occurring in the airway. This
model considers a three-dimensional geometry of vocal folds, muscle contractions, and viscoelastic proper-
ties to provide a realistic framework of phonation. The vocal fold motion is coupled to an unsteady com-
pressible respiratory flow, allowing numerical simulations of normal and diseased phonations to derive clear
relationships between actual laryngeal structures and model parameters such as muscle activity. As a pilot
analysis of diseased phonation, we model vocal nodules, the mass lesions that can appear bilaterally on both
sides of the vocal folds. Comparison of simulations with and without the nodules demonstrates how the le-
sions affect vocal fold motion, consequently restricting voice quality. Furthermore, we found that the mini-
mum lung pressure required for voice production increases as nodules move closer to the center of the vocal
fold. Thus, simulations using the developed model may provide essential insight into complex phonation
phenomena and further elucidate the etiologic mechanisms of voice disorders.
Keywords: Aerodynamics, Flow-Structure Interaction, Self-Excited Oscillation, Phonation, Vocal Fold,
Larynx, Vocal Tract, Speech Production, Voice Production, Vocal Nodules, Vocal Cord Polyp,
Voice Disorder
1. Introduction
Human phonation consists of the following mechanical
processes: 1) induction of self-excited vocal fold oscilla-
tions by respiratory airflow through flow-structure inter-
action, 2) acoustic resonance of sounds generated by the
oscillations in the airway, i.e., the passage from the lungs
to the mouth and nose, and 3) emission of the sounds to
the surrounding atmosphere as voice. Mathematical
modeling and computer simulation of phonation, thus a
complicated mechanical phenomenon, may be useful for
future clinical diagnosis and therapy of diseased or in-
jured vocal folds.
Various numerical models have been reported for
phonation simulation. One of the earliest was provided
by Ishizaka and Flanagan [1], in which the vocal folds
were approximated by two connected masses supported
by nonlinear springs and dampers. In addition to flow-
induced self-excitation of the vocal folds as a source of
voice sound, their model considered virtually all me-
chanical phenomena occurring during phonation, includ-
ing sound resonance in the vocal tract (i.e., the pharynx
and the oral and nasal cavities) and sound emission into
the atmosphere. However, structural and histological
details for the vocal folds were not incorporated in their
lumped two-mass model. To identify the etiology of voice
disorders based on such simulations, vocal fold models
are required to capture relevant anatomical and func-
tional characteristics [2]. Story and Titze [3] proposed an
alternative vocal fold model consisting of three masses,
i.e., a deep mass representing the body of the vocal fold
(modeling the thyroarytenoid (TA) muscle and the deep
layer of the lamina propria) and the other two masses
representing the cover of the vocal fold (modeling the
epithelium as well as the superficial and intermediate
layers of the lamina propria). Two-dimensional vocal fold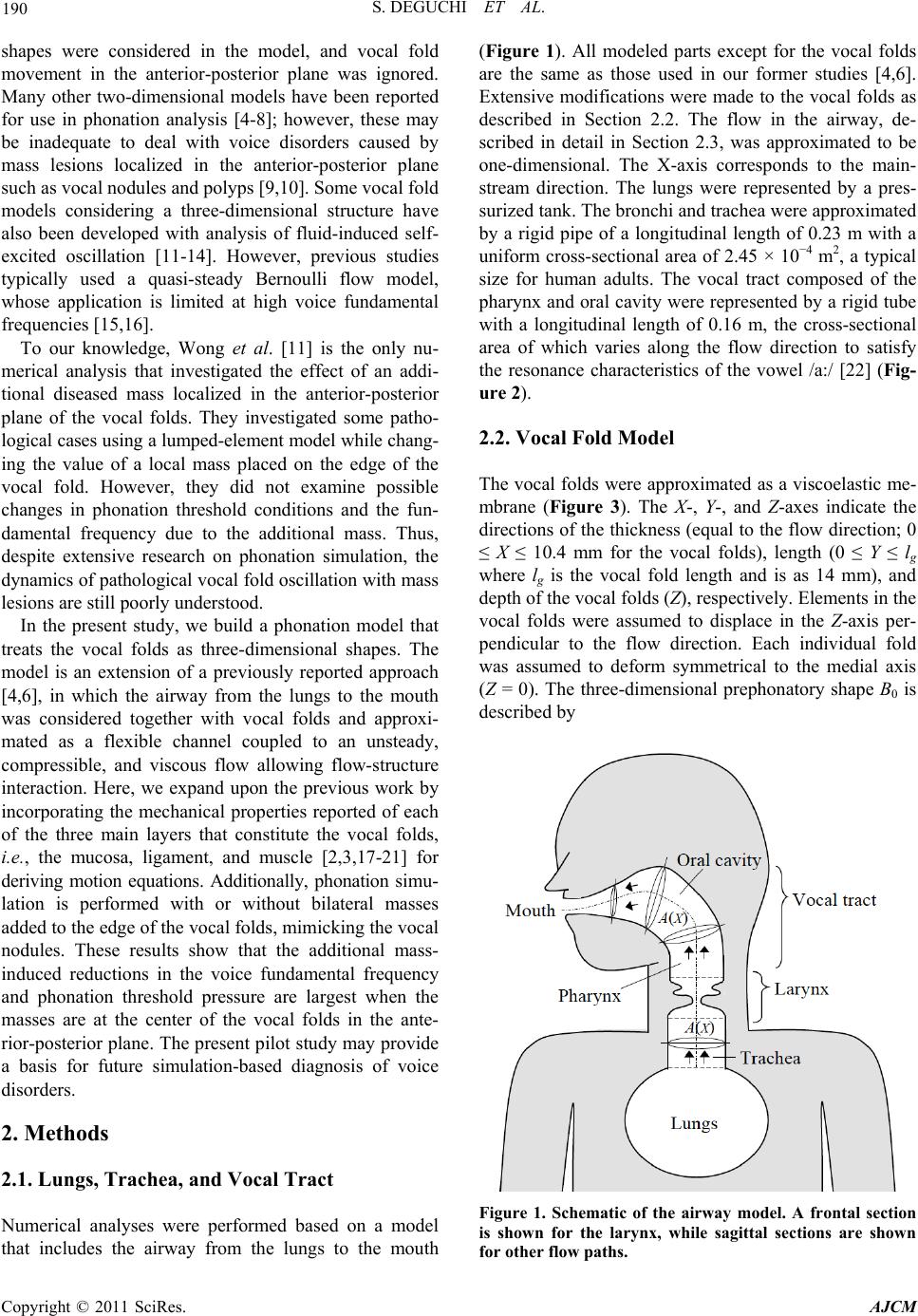

190 S. DEGUCHI ET AL.
shapes were considered in the model, and vocal fold
movement in the anterior-posterior plane was ignored.
Many other two-dimensional models have been reported
for use in phonation analysis [4-8]; however, these may
be inadequate to deal with voice disorders caused by
mass lesions localized in the anterior-posterior plane
such as vocal nodules and polyps [9,10]. Some vocal fold
models considering a three-dimensional structure have
also been developed with analysis of fluid-induced self-
excited oscillation [11-14]. However, previous studies
typically used a quasi-steady Bernoulli flow model,
whose application is limited at high voice fundamental
frequencies [15,16].
To our knowledge, Wong et al. [11] is the only nu-
merical analysis that investigated the effect of an addi-
tional diseased mass localized in the anterior-posterior
plane of the vocal folds. They investigated some patho-
logical cases using a lumped-element model while chang-
ing the value of a local mass placed on the edge of the
vocal fold. However, they did not examine possible
changes in phonation threshold conditions and the fun-
damental frequency due to the additional mass. Thus,
despite extensive research on phonation simulation, the
dynamics of pathological vocal fold oscillation with mass
lesions are still poorly understood.
In the present study, we build a phonation model that
treats the vocal folds as three-dimensional shapes. The
model is an extension of a previously reported approach
[4,6], in which the airway from the lungs to the mouth
was considered together with vocal folds and approxi-
mated as a flexible channel coupled to an unsteady,
compressible, and viscous flow allowing flow-structure
interaction. Here, we expand upon the previous work by
incorporating the mechanical properties reported of each
of the three main layers that constitute the vocal folds,
i.e., the mucosa, ligament, and muscle [2,3,17-21] for
deriving motion equations. Additionally, phonation simu-
lation is performed with or without bilateral masses
added to the edge of the vocal folds, mimicking the vocal
nodules. These results show that the additional mass-
induced reductions in the voice fundamental frequency
and phonation threshold pressure are largest when the
masses are at the center of the vocal folds in the ante-
rior-posterior plane. The present pilot study may provide
a basis for future simulation-based diagnosis of voice
disorders.
2. Methods
2.1. Lungs, Trachea, and Vocal Tract
Numerical analyses were performed based on a model
that includes the airway from the lungs to the mouth
(Figure 1). All modeled parts except for the vocal folds
are the same as those used in our former studies [4,6].
Extensive modifications were made to the vocal folds as
described in Section 2.2. The flow in the airway, de-
scribed in detail in Section 2.3, was approximated to be
one-dimensional. The X-axis corresponds to the main-
stream direction. The lungs were represented by a pres-
surized tank. The bronchi and trachea were approximated
by a rigid pipe of a longitudinal length of 0.23 m with a
uniform cross-sectional area of 2.45 × 10−4 m2, a typical
size for human adults. The vocal tract composed of the
pharynx and oral cavity were represented by a rigid tube
with a longitudinal length of 0.16 m, the cross-sectional
area of which varies along the flow direction to satisfy
the resonance characteristics of the vowel /a:/ [22] (Fig-
ure 2).
2.2. Vocal Fold Model
The vocal folds were approximated as a viscoelastic me-
mbrane (Figure 3). The X-, Y-, and Z-axes indicate the
directions of the thickness (equal to the flow direction; 0
≤ X ≤ 10.4 mm for the vocal folds), length (0 ≤ Y ≤ lg
where lg is the vocal fold length and is as 14 mm), and
depth of the vocal folds (Z), respectively. Elements in the
vocal folds were assumed to displace in the Z-axis per-
pendicular to the flow direction. Each individual fold
was assumed to deform symmetrical to the medial axis
(Z = 0). The three-dimensional prephonatory shape B0 is
described by
Figure 1. Schematic of the airway model. A frontal section
is shown for the larynx, while sagittal sections are shown
for other flow paths.

S. DEGUCHI ET AL.
191
Figure 2. Cross-sectional area distribution of the vocal tract
for the vowel /a:/. The horizontal axis is the distance from
the upstream end of the vocal tract to the end of the larynx
or false vocal folds (see Figure 3).



o
3
03
o
2
2
o
210.4tan 49
10.4
3210.4tan49
10.4
tan49mm,
en ex
en ex
en
BB
BX
BB
X
XB





(1)

1
ex vpg
BB Yl

, (2)
where Ben (fixed to be 8.2 mm) and Bex are the half-glot-
tal widths at the entrance (X = 0 mm) and exit (X = 10.4
mm), respectively, and Bvp is the half-glottal width at the
tip of the vocal process of the arytenoid cartilages (X =
10.4 mm; Y = 0 mm) (Figure 3). Even when Bvp is 0 mm,
it is assumed that the glottis has a small rear gap (poste-
rior glottis) between the separate arytenoid cartilages that
do not vibrate during phonation. The prephonatory shape
within the X-Z plane is described in detail in previous
studies [6].
Following the body-cover theory [17,19], the vocal
folds are assumed to consist of three layers, the mucosa,
ligament, and TA muscle. The mucosa, representing the
epithelium and superficial layer of the lamina propria,
covers the vocal folds. The vocal ligament, underlying
the mucosa and overlying the muscle, consists of inter-
mediate and deep layers of the lamina propria. It has an
anterior-posterior orientation between the anterior com-
missure (Y = lg) and vocal processes (Y = 0 cm). The TA
muscle is juxtaposed to the ligament. It is assumed that
no relative displacement occurs between the interfaces of
each layer. The equation of motion is derived consider-
ing the force balance for an infinitesimal element in the
vocal fold (Figure 3) given as


2
2
sin
sin ,
yy
xx
vcol
T
T
B
hFP XY
T





  (3)
2
sin1 ,
x
BB
XX






(4)
(a)
(b)
Figure 3. Schematic of the larynx model. (a) Initial geome-
try of vocal fold model in the coronal (X-Z) plane. (b) Upper
view (Y-Z plane) of the vocal folds. Open triangles represent
the tips of the vocal process of arytenoid muscle and ante-
rior commissure where no displacement is permitted during
oscillation. Asterisks represent the plane shown in (a).
2
sin1 ,
y
BB
YY






(5)
where v

is the mass per unit volume, h is the vocal
fold depth effective for vibration, B is the half-glottal
width, T is the time, Fcol is the collision force per unit
area, P is the static air pressure, Tx and Ty are tensions in
the vocal folds in the X- and Y-directions, respectively,
and
x

and
y

are deformed angles of infinitesimal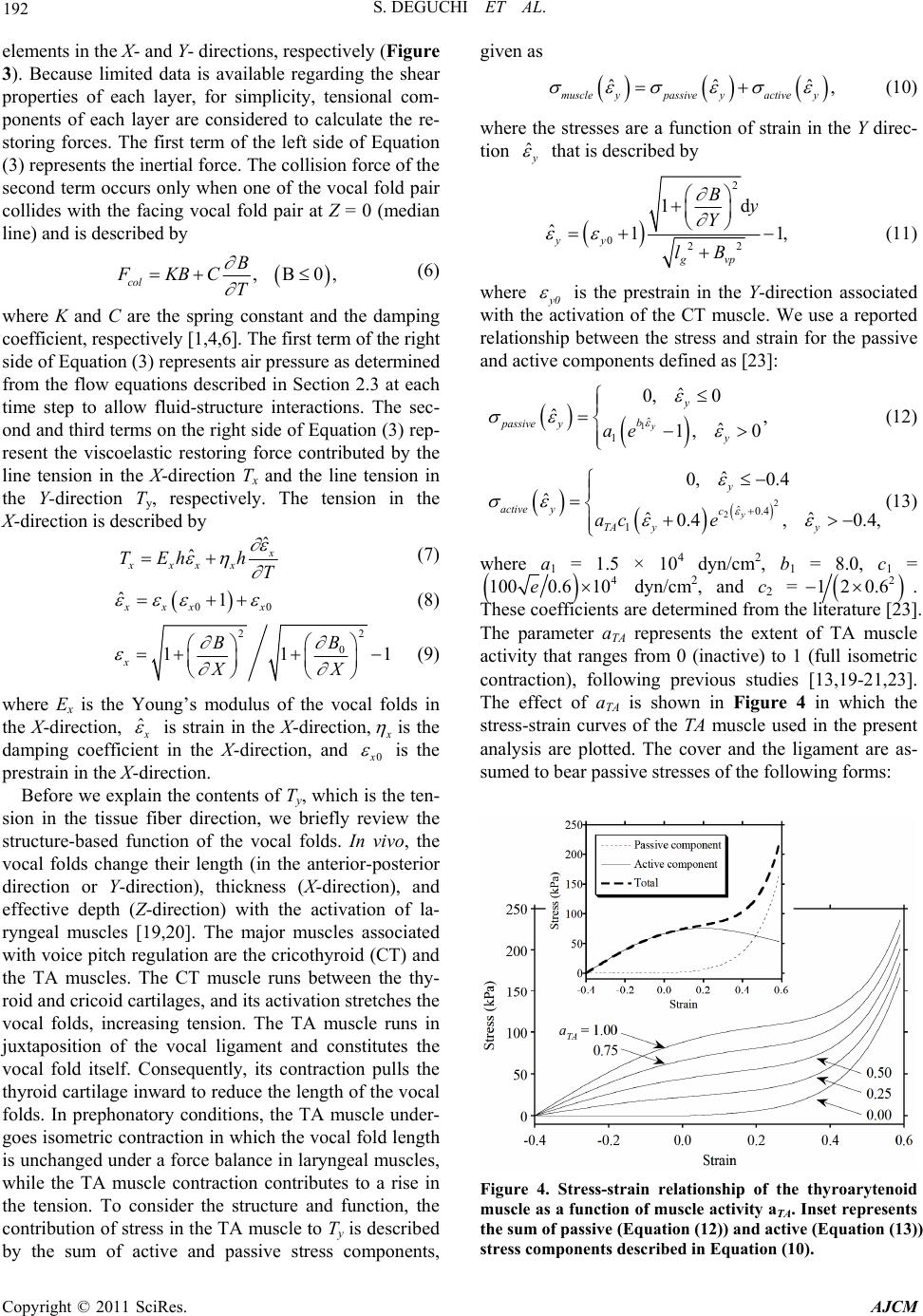

192 S. DEGUCHI ET AL.
elements in the X- and Y- directions, respectively (Figure
3). Because limited data is available regarding the shear
properties of each layer, for simplicity, tensional com-
ponents of each layer are considered to calculate the re-
storing forces. The first term of the left side of Equation
(3) represents the inertial force. The collision force of the
second term occurs only when one of the vocal fold pair
collides with the facing vocal fold pair at Z = 0 (median
line) and is described by

, B0,
col
B
FKBC
T



  (6)
where K and C are the spring constant and the damping
coefficient, respectively [1,4,6]. The first term of the right
side of Equation (3) represents air pressure as determined
from the flow equations described in Section 2.3 at each
time step to allow fluid-structure interactions. The sec-
ond and third terms on the right side of Equation (3) rep-
resent the viscoelastic restoring force contributed by the
line tension in the X-direction Tx and the line tension in
the Y-direction T
y, respectively. The tension in the
X-direction is described by
ˆ
ˆ
x
xxxx
TEh h
T




 (7)

0
ˆ10
x
xx x

   (8)
2 2
0
11
x
B B
XX
 

 
 
 
 
1
(9)
where Ex is the Young’s modulus of the vocal folds in
the X-direction, ˆ
x

is strain in the X-direction,
x

is the
damping coefficient in the X-direction, and 0
x

is the
prestrain in the X-direction.
Before we explain the contents of Ty, which is the ten-
sion in the tissue fiber direction, we briefly review the
structure-based function of the vocal folds. In vivo, the
vocal folds change their length (in the anterior-posterior
direction or Y-direction), thickness (X-direction), and
effective depth (Z-direction) with the activation of la-
ryngeal muscles [19,20]. The major muscles associated
with voice pitch regulation are the cricothyroid (CT) and
the TA muscles. The CT muscle runs between the thy-
roid and cricoid cartilages, and its activation stretches the
vocal folds, increasing tension. The TA muscle runs in
juxtaposition of the vocal ligament and constitutes the
vocal fold itself. Consequently, its contraction pulls the
thyroid cartilage inward to reduce the length of the vocal
folds. In prephonatory conditions, the TA muscle under-
goes isometric contraction in which the vocal fold length
is unchanged under a force balance in laryngeal muscles,
while the TA muscle contraction contributes to a rise in
the tension. To consider the structure and function, the
contribution of stress in the TA muscle to Ty is described
by the sum of active and passive stress components,
given as


ˆˆ ,
muscle ypassive yactive y

ˆ

   (10)
where the stresses are a function of strain in the Y direc-
tion ˆ
y

that is described by

2
022
1d
ˆ1
yy
gvp
By
Y
lB





 1
,


 (11)
where
y
0

is the prestrain in the Y-direction associated
with the activation of the CT muscle. We use a reported
relationship between the stress and strain for the passive
and active components defined as [23]:


1ˆ
1
ˆ
0, 0
ˆ,
ˆ
1, 0
y
y
b
passive y
y
ae


 








(12)
 

2
2ˆ0.4
1
ˆ 0, 0.4
ˆ
ˆˆ
0.4, 0.4,
y
y
active yc
TA yy
ac e


 







(13)
where a1 = 1.5 × 104 dyn/cm2, b1 = 8.0, c1 =


4
1000.6 10e dyn/cm2, and c2 =


2
120.6 .
These coefficients are determined from the literature [23].
The parameter aTA represents the extent of TA muscle
activity that ranges from 0 (inactive) to 1 (full isometric
contraction), following previous studies [13,19-21,23].
The effect of aTA is shown in Figure 4 in which the
stress-strain curves of the TA muscle used in the present
analysis are plotted. The cover and the ligament are as-
sumed to bear passive stresses of the following forms:
Figure 4. Stress-strain relationship of the thyroarytenoid
muscle as a function of muscle activity aTA. Inset represents
the sum of passive (Equation (12)) and active (Equation (13))
stress components described in Equation (10).

S. DEGUCHI ET AL.
193

 


2ˆ
2
ˆ 0, 0
ˆ
ˆ
1, 0,
y
y
cover yb
y
ae


 





(14)
 


3ˆ
3
ˆ
0, 0
ˆ
ˆ 1, 0,
y
y
ligament yb
y
ae


 





(15)
where a2 = 7.1 × 104 dyn/cm2, b2 = 4.2, a3 = 5.56 × 104
dyn/cm2, and b3 = 5.15. These stress–strain relationships
are also based on data shown in the previous literature
[23]. Consequently, the tension in the vocal folds ob-
tained from the stresses in the three layers is given as
 

ˆˆ
ˆ
ˆ
,
y
m muscleylligamenty
y
c coveryy
Th h
hh
T

 




 (16)
where hm, hl, and hc are the depths of the muscle, the
ligament, and the cover layers, respectively, and
y

is a
damping coefficient. The last term represents tissue
damping that is assumed to be proportional to the first
time derivative of
y

.
2.3. Flow Model
Airflow is described by the following equations of con-
tinuity and motion for a one-dimensional unsteady, com-
pressible, and viscous flow [4,6,15,16]:
2
a0,
PP AQ
AQ a
TX TX
 

 

 


(17)
2
a
11
0,
2
QQP
G
TA XAX
 

 

 
 
(18)
where A, Q, a

, a, and G are the cross-sectional areas of
the airway, volume flow, air density, sound speed, and
viscous terms, respectively. To evaluate pressure distri-
bution along the false glottis, airflow is assumed to
separate at the downstream end of the glottis, become a
parallel side jet, and reattach at the downstream end of
the false glottis [4,6,24] (Figure 3). The false glottis is
assumed not to deform. The flow streamline after separa-
tion is assumed to have a quartic curve shape based on
fluid mechanical experiments and analyses [24]. The
Hagen-Poiseuille velocity distribution with kinematic
viscosity

is assumed only for evaluation of the vis-
cous term G. Here, a rectangular geometry with a depth
of L (equal to the vocal fold length) is assumed for the
cross-section of the glottis. For the other airway, circular
cylindrical flow paths are assumed. Consequently,
3
32
Q
GLB   (19)
for the glottis (L = 14 + 3 = 17 mm; Figure 3(b)) and
2
8πQ G
A
  (20)
for the other flow paths.
2.4. Simulation
At the upstream end of the trachea, the total pressure is
assumed to be equal to the lung pressure. Phonation is
assumed to be initiated by increasing the lung pressure Pl
in the following manner [4,6]:


π
1cos
2, 0
,
ls
p
lp
ls p
PT
T
PT
PTT







 





T (21)
where Pls and Tp are the final value of Pl and the time
required to achieve Pls, respectively. The pressure at the
downstream end of the airway (i.e., the mouth) is given
by the following equation that represents a radiation load
on a circular piston in an infinite baffle [1]:
3
8.
3
A
U
PT




 (22)
It is assumed that no displacement of the vocal folds oc-
curs at the anterior commissure (Y = lg) and the arytenoid
muscle (Y = −3 mm to 0 mm) along the X-axis (Figure 3).
For phonation simulation with bilateral vocal nodules,
an additional mass of MVN = 0.15 g is added to each vo-
cal fold pair. Unless otherwise stated, the bilateral
masses are localized to a point at the supraglottis (X =
10.4 mm) close to the center of the vocal fold length (Y =
6.4 mm), i.e., the size of the vocal nodules is assumed to
be zero in this case. To evaluate the effect of the local-
ized mass, the mass is increased in value by a factor of
1.25 or 1.5. Alternatively, the additional masses placed at
the supraglottis were distributed at either 1) Y = 6.4 mm
and Y = 7.4 mm (assuming that nodule size = 1 mm) or 2)
Y = 5.4 mm, Y = 6.4 mm, and Y = 7.4 mm (assuming that
nodule size = 2 mm). It is likely that appearance of vocal
nodules results in a localized change in stiffness as well
as mass of the folds. In our preliminary analysis, we ob-
served that a localized change in stiffness in the vocal
fold model resulted in chaotic vocal fold motions and
sound waveforms, which was not observed with isolated
changes in mass. This behavior is consistent with our
previous analysis using a two-dimensional model [4,6],
in which a change in stiffness sometimes results in a
chaotic behavior. However, a thorough analysis is needed
to understand the range of observed chaotic behavior,
which will be a subject of future investigation. The pre-
sent analysis, as a pilot study, only investigates the effect

194 S. DEGUCHI ET AL.
of the addition of localized masses in the three-dimen-
sional geometry.
An implicit time-differencing scheme is applied [4] to
integrate the flow equations, Equations (17) and (18).
The flow equations are coupled to the motion equation,
Equation (3). The time increment is chosen to be 1.0 ×
10−5 s. Table 1 lists the values of other fixed parameters
used throughout the simulation.
3. Results
3.1. Wavelike Motion of the Vocal Fold Model
Similar to the Actual Behavior
Numerical simulation of normal human phonation with-
out nodules was performed to evaluate the validity of our
model. As the lung pressure increased according to Eq-
uation (1), a small-amplitude oscillatory motion arose in
the vocal folds via the fluid-structure interaction. The
small motion gradually grew larger and spread over the
entire vocal folds. At a steady state of established limit
cycles (Figure 5), the glottis opened at the upstream sub-
glottis first and then at the downstream supraglottis.
Similarly, closure first occurred upstream then down-
stream, consistent with the wavelike motion of actual
vocal folds or a rubber-sheet model [25]. Pronounced
collisions between the facing vocal folds occurred at the
supraglottal region. The observation of the downstream
end (Bex) from the top view (Y-Z plane) showed relative
motion between the anterior and posterior regions. Dur-
ing the process of initial oscillation development, ante-
rior and posterior parts of the vocal folds moved nearly
in the same phase (figure not shown). However, anterior
preceded the posterior in phase at later steady-state con-
ditions (Figure 6).
3.2. Effect of Adduction on Fundamental
Frequency
The observed phase lead probably resulted from the
slightly abducted glottal geometry of the posterior region,
causing it to undergo a relatively weak interaction with
the fluid. This resulted in a delayed reaction to flow
compared to the anterior narrow glottal width and strong
flow-structure interaction. Therefore, we investigated the
effect of laryngeal adduction by changing the posterior
glottis angle Φ as follows (Figure 3(b)):

13tan mm
vp
B 

(23)
The fundamental frequency of the steady-state oscilla-
tion increased as the vocal folds were more adducted
(decrease in Φ) at any TA muscle activity aTA (Figure
7(a)) and lung pressure (Figures 7(b) and (c)). Increase
in the fundamental frequency of the self-excited oscilla-
tions reflects closer interaction between the structure and
the fluid [16], consistent with the above interpretation.
3.3. Effect of Bilaterally Localized Masses on
Phonation
Next, we investigated how the presence of bilaterally
localized masses, which approximate the vocal nodules,
affected the fold motion. The oscillatory motion was de-
layed in phase locally around the place of nodules (Fig-
ure 8; arrowhead). Therefore, it appeared that the ante-
rior part, the nodule, and the posterior part moved like
three masses interconnected by springs. At the same time,
the anterior and posterior parts had a smooth second
mode deformation. Consequently, in the Y-Z plane, the
vocal folds behaved similar to both a three-mass model
and a four-mass model. Indeed, total pressure waveform
at the mouth, corresponding to the produced voice, had a
relatively high intensity at the third and fourth harmonics
(Figure 9). On the other hand, the sound waveform ob-
tained from the smooth normal vocal fold oscillation
without nodules predominantly peaked at lower fre-
quency second harmonics.
Table 1. Fixed model parameters.
SymbolMeaning Value
a Sound speed 3.5 × 102 m/sa
C Additional damping constant 103 Ns/m3b
Ex Young’s modulus (X-axis) 4.0 × 105 N/m2a
h Vocal fold thickness 2 mmd
hc Cover thickness 0.35 mme
hl Ligament thickness 0.8 mme
hm Muscle thickness 0.85 mme
K Additional spring constant 1.0 × 106 N/m3a,c
Tp Time constant in Equation (21) 1.0 × 10–2 sa
εx0 Prestrain (X-axis) 0.2f
εy0 Prestrain (Y-axis) 0.2f
ηx Damping coefficient (X-axis) 102 Ns/m2g
ηy Damping coefficient (Y-axis) 102 Ns/m2g
υ Viscosity 1.7 × 10–5 m2/sa
ρa Air density 1.1 kg/m3a
ρv Vocal fold density 1.03 × 103 kg/m3e
aIkeda et al., 2001. bEstimated from
 
2121 0.3hK hK   
vv
cIshizaka and Flanagan, 1972. dh = hc + hl + hm. eStory and Titze, 1995.
.a,c
fDeguchi and Kawahara, 2011. gEstimated from lgC.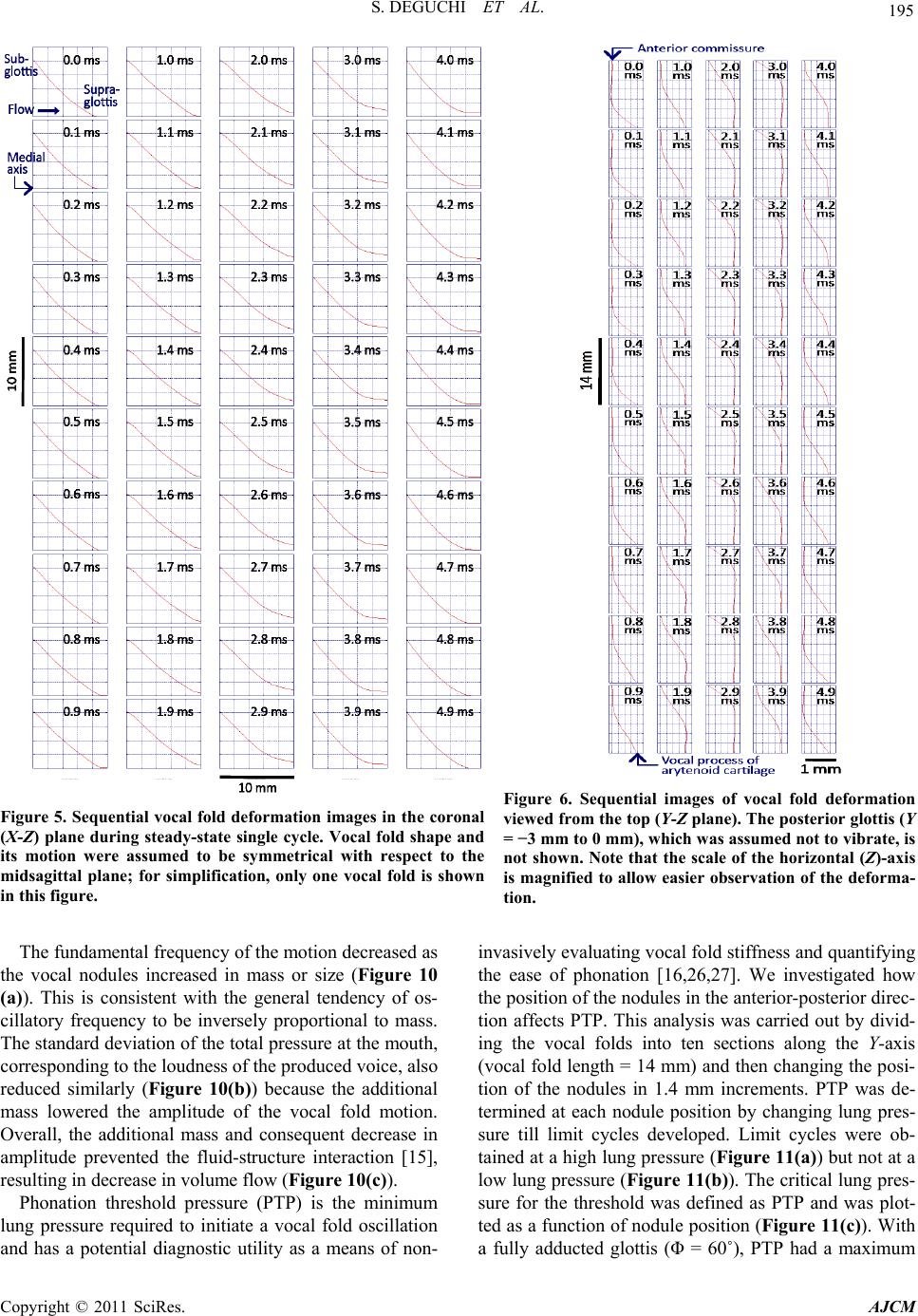

S. DEGUCHI ET AL.
195
Figure 6. Sequential images of vocal fold deformation
viewed from the top (Y-Z plane). The posterior glottis (Y
= −3 mm to 0 mm), which was assumed not to vibrate, is
not shown. Note that the scale of the horizontal (Z)-axis
is magnified to allow easier observation of the deforma-
tion.
Figure 5. Sequential vocal fold deformation images in the coronal
(X-Z) plane during steady-state single cycle. Vocal fold shape and
its motion were assumed to be symmetrical with respect to the
midsagittal plane; for simplification, only one vocal fold is shown
in this figure.
The fundamental frequency of the motion decreased as
the vocal nodules increased in mass or size (Figure 10
(a)). This is consistent with the general tendency of os-
cillatory frequency to be inversely proportional to mass.
The standard deviation of the total pressure at the mouth,
corresponding to the loudness of the produced voice, also
reduced similarly (Figure 10(b)) because the additional
mass lowered the amplitude of the vocal fold motion.
Overall, the additional mass and consequent decrease in
amplitude prevented the fluid-structure interaction [15],
resulting in decrease in volume flow (Figure 10(c)).
Phonation threshold pressure (PTP) is the minimum
lung pressure required to initiate a vocal fold oscillation
and has a potential diagnostic utility as a means of non-
invasively evaluating vocal fold stiffness and quantifying
the ease of phonation [16,26,27]. We investigated how
the position of the nodules in the anterior-posterior direc-
tion affects PTP. This analysis was carried out by divid-
ing the vocal folds into ten sections along the Y-axis
(vocal fold length = 14 mm) and then changing the posi-
tion of the nodules in 1.4 mm increments. PTP was de-
termined at each nodule position by changing lung pres-
sure till limit cycles developed. Limit cycles were ob-
tained at a high lung pressure (Figure 11(a)) but not at a
low lung pressure (Figure 11(b)). The critical lung pres-
sure for the threshold was defined as PTP and was plot-
ted as a function of nodule position (Figure 11(c)). With
a fully adducted glottis (Φ = 60˚), PTP had a maximum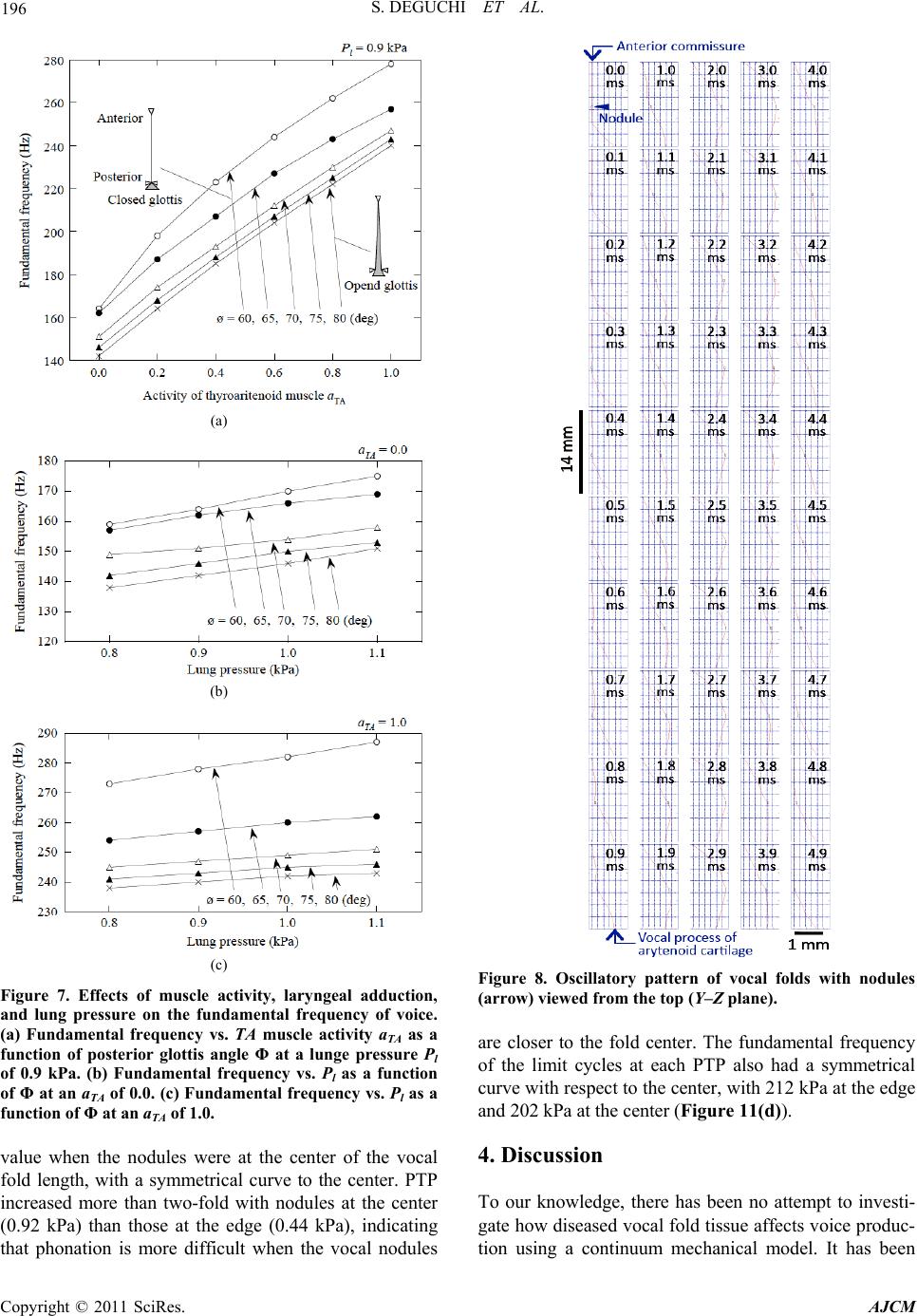

196 S. DEGUCHI ET AL.
(a)
(b)
(c)
Figure 7. Effects of muscle activity, laryngeal adduction,
and lung pressure on the fundamental frequency of voice.
(a) Fundamental frequency vs. TA muscle activity aTA as a
function of posterior glottis angle Φ at a lunge pressure Pl
of 0.9 kPa. (b) Fundamental frequency vs. Pl as a function
of Φ at an aTA of 0.0. (c) Fundamental frequency vs. Pl as a
function of Φ at an aTA of 1.0.
value when the nodules were at the center of the vocal
fold length, with a symmetrical curve to the center. PTP
increased more than two-fold with nodules at the center
(0.92 kPa) than those at the edge (0.44 kPa), indicating
that phonation is more difficult when the vocal nodules
Figure 8. Oscillatory pattern of vocal folds with nodules
(arrow) viewed from the top (Y–Z plane).
are closer to the fold center. The fundamental frequency
of the limit cycles at each PTP also had a symmetrical
curve with respect to the center, with 212 kPa at the edge
and 202 kPa at the center (Figure 11(d)).
4. Discussion
To our knowledge, there has been no attempt to investi-
gate how diseased vocal fold tissue affects voice produc-
tion using a continuum mechanical model. It has been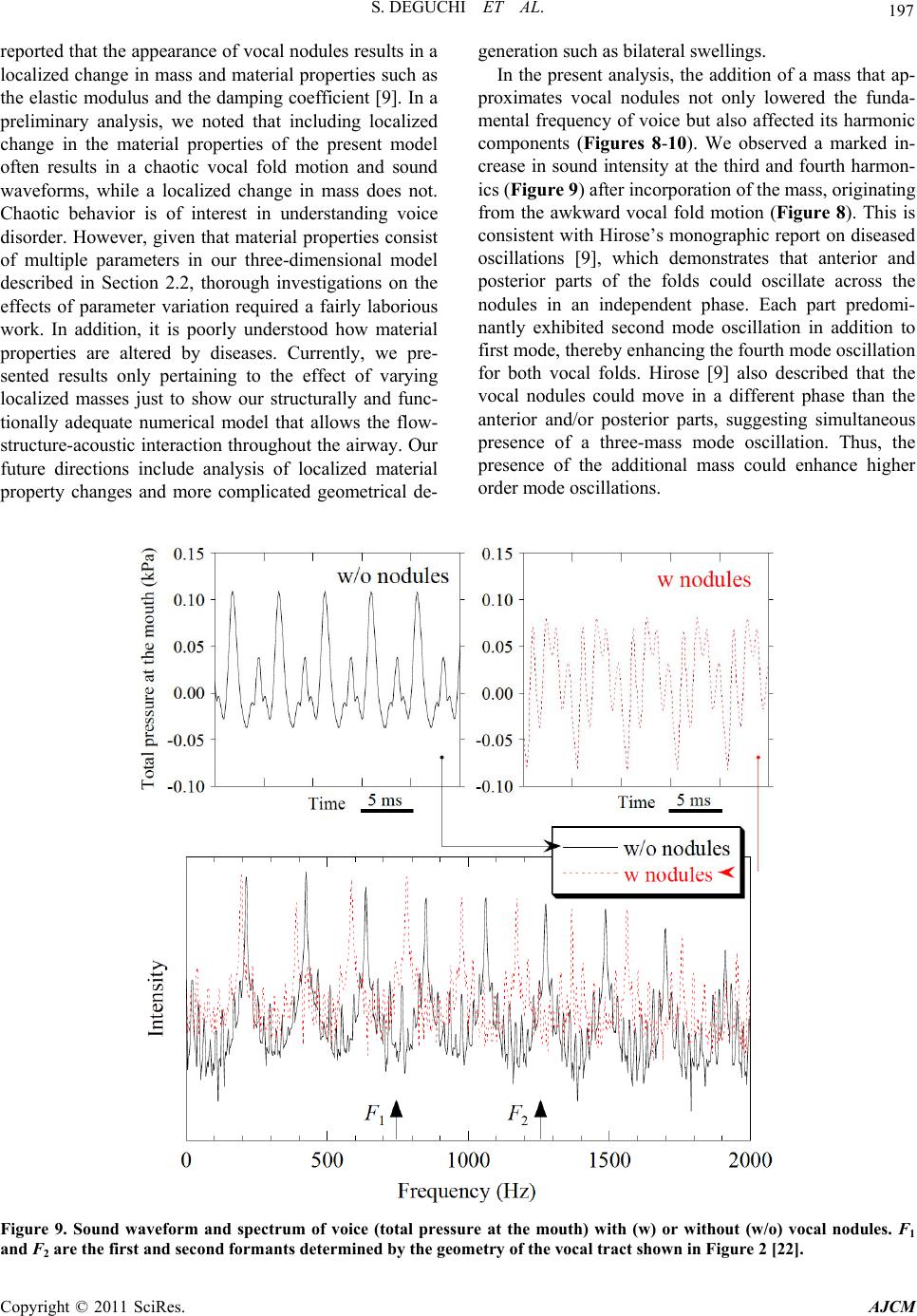

S. DEGUCHI ET AL.
197
reported that the appearance of vocal nodules results in a
localized change in mass and material properties such as
the elastic modulus and the damping coefficient [9]. In a
preliminary analysis, we noted that including localized
change in the material properties of the present model
often results in a chaotic vocal fold motion and sound
waveforms, while a localized change in mass does not.
Chaotic behavior is of interest in understanding voice
disorder. However, given that material properties consist
of multiple parameters in our three-dimensional model
described in Section 2.2, thorough investigations on the
effects of parameter variation required a fairly laborious
work. In addition, it is poorly understood how material
properties are altered by diseases. Currently, we pre-
sented results only pertaining to the effect of varying
localized masses just to show our structurally and func-
tionally adequate numerical model that allows the flow-
structure-acoustic interaction throughout the airway. Our
future directions include analysis of localized material
property changes and more complicated geometrical de-
generation such as bilateral swellings.
In the present analysis, the addition of a mass that ap-
proximates vocal nodules not only lowered the funda-
mental frequency of voice but also affected its harmonic
components (Figures 8-10). We observed a marked in-
crease in sound intensity at the third and fourth harmon-
ics (Figure 9) after incorporation of the mass, originating
from the awkward vocal fold motion (Figure 8). This is
consistent with Hirose’s monographic report on diseased
oscillations [9], which demonstrates that anterior and
posterior parts of the folds could oscillate across the
nodules in an independent phase. Each part predomi-
nantly exhibited second mode oscillation in addition to
first mode, thereby enhancing the fourth mode oscillation
for both vocal folds. Hirose [9] also described that the
vocal nodules could move in a different phase than the
anterior and/or posterior parts, suggesting simultaneous
presence of a three-mass mode oscillation. Thus, the
presence of the additional mass could enhance higher
order mode oscillations.
Figure 9. Sound waveform and spectrum of voice (total pressure at the mouth) with (w) or without (w/o) vocal nodules. F1
and F2 are the first and second formants determined by the geometry of the vocal tract shown in Figure 2 [22].

198 S. DEGUCHI ET AL.
(a)
(b)
(c)
Figure 10. Effects of the vocal nodules on voice quality. The size of the vocal nodules vs. fundamental frequency (a), standard
deviation of the total pressure at the mouth (corresponding to loudness of the voice) (b), and mean value of the volume flow at
the supraglottis (X = 10.4 mm) (c) as a function of their masses.

S. DEGUCHI ET AL.
199
PTP was because of increase in tissue stiffness, without
change in the mass or the interactive dimension.
The fundamental frequency was the lowest when the
nodules were located at the center of fully adducted vo-
cal fold length (Figure 11(d)). PTP, which can vary as a
function of the fundamental frequency of voice, was
greatest in the same nodule position (Figure 11(c)). As
the nodules moved to the edge of the vocal fold length,
the freely movable portion increased, allowing an easier
onset of phonation (i.e. , smaller PTP; Figure 11(c)) and
a closer fluid-structure interaction (i.e., higher fundamen-
tal frequency; Figure 11(d)) [15]. Thus, the close asso-
ciation between the vocal fold motion and the voice fre-
quency as well as the ease of phonation was influenced
by the position of the vocal nodules. The negative corre-
lation of Figures 11(c) and (d) shown in this model con-
tradicts an analytical result previously reported [16]
which states that PTP increases with the fundamental
frequency. In previous findings, PTP increased with tis-
sue stiffness or mass but decreased with the fluid-struc-
ture interactive geometric dimension (Equation (24))
[16]. However, this can be reconciled by noting that the
fundamental frequency elevation that caused a rise in
The present model considers the three-dimensional
geometry of the vocal folds and functional ability of in-
corporating active (muscular) and passive (ligamentous)
stresses in the layered structure. Thus, clear relationships
between the actual laryngeal structure and the model are
observed, potentially allowing for more sophisticated
simulation of disease conditions such as recurrent pa-
ralysis and vocal polyps. However, the model is not
without limitations. In particular, initial glottal geometry
in Equations (1) and (2) is determined independent of
muscle activation. TA muscle activation was considered
only for evaluating the tissue restoring force in Equation
(13). The CT muscle activation was only implied for
determination of the prestrains in Equations (8) and (11).
In vivo, these muscle activations not only regulate the
restoring force and prestrain but also determine the pre-
phonatory positions of the laryngeal cartilages and vocal
fold geometry, as discussed elsewhere [19-21]. Thus, the
incorporation of muscle-dependent regulation of the pre-
phonatory structure may be a desirable future direction.
(a) (b)
(c) (d)
Figure 11. Effects of the vocal nodules on phonation efficiency. (a, b) Time course of cross-sectional area of the glottis at dif-
ferent lung pressures. Limit cycles are established at a high lung pressure Pls (a), while the oscillations gradually attenuate at
low Pls (b). (c, d) Phonation threshold lung pressure and fundamental frequency of voice have an inverted v-letter and a
v-letter curve, respectively, with respect to the position of the vocal nodules along the vocal fold length.

S. DEGUCHI ET AL.
200
In summary, we have developed a continuum-based
numerical model for the simulation of human phonation
with diseased vocal fold tissue. Here, we focused on the
effect of varying localized bilateral masses to approxi-
mate the vocal nodules. The result shows that the presence
of the nodules lowers the voice fundamental frequency
and intensity. Phonation efficiency is most strongly de-
creased when the nodules are close to the center of the
vocal fold length, where they prevent the fluid-structure
interactions responsible for source sound production.
These results suggest that phonation simulation using the
newly developed model may be useful for indentifying
the etiology of voice disorders.
5. Acknowledgements
The authors thank Yuji Matsuzaki and Tadashige Ikeda
for providing advice on study design and Seiichi Washio
and Satoshi Takahashi for discussion. SD gratefully ac-
knowledges the support from the Japan Science and
Technology Agency. This work was supported in part by
Grant-in-Aid from the Ministry of Education, Culture,
Sports, Science, and Technology of Japan (#19700382 to
SD).
6. References
[1] K. Ishizaka and J. L. Flanagan, “Synthesis of Voiced
Sounds from a Two-Mass Model of the Vocal Cords,”
Bell System Technical Journal, Vol. 51, No. 6, 1972, pp.
1233-1268.
[2] M. Hirano, “Morphological Structure of the Vocal Cord
as a Vibrator and Its Variations,” Folia Phoniatrica et
Logopaedica, Vol. 26, No. 2, 1974, pp. 89-94.
doi:10.1159/000263771
[3] B. H. Story and I. R. Titze, “Voice Simulation with a
Body-Cover Model of the Vocal Folds,” Journal of the
Acoustical Society of America, Vol. 97, No. 2, 1995, pp.
1249-1260. doi:10.1121/1.412234
[4] T. Ikeda, Y. Matsuzaki and T. Aomatsu, “A Numerical
Analysis of Phonation Using a Two-Dimensional Flexi-
ble Channel Model of the Vocal Folds,” Journal of Bio-
mechanical Engineering, Vol. 123, No. 6, 2001, pp. 571-
579. doi:10.1115/1.1408939
[5] C. Tao, J. J. Jiang and Y. Zhang, “Simulation of Vocal
Fold Impact Pressures with a Self-Oscillating Finite-Ele-
ment Model,” Journal of the Acoustical Society of Amer-
ica, Vol. 119, No. 6, 2006, pp. 3987-3994.
doi:10.1121/1.2197798
[6] S. Deguchi, Y. Matsuzaki and T. Ikeda, “Numerical Analy-
sis of Effects of Transglottal Pressure Change on Funda-
mental Frequency of Phonation,” Annals of Otology, Rhi-
nology and Laryngology, Vol. 116, No. 2, 2007, pp.
128-134.
[7] I. T. Tokuda, J. Horácek, J. G. Svec and H. Herzel,
“Comparison of Biomechanical Modeling of Register
Transitions and Voice Instabilities with Excised Larynx
Experiments,” Journal of the Acoustical Society of Amer-
ica, Vol. 122, No. 1, 2007, pp. 519-531.
doi:10.1121/1.2741210
[8] X. Zheng, S. Bielamowicz, H. Luo and R. Mittal, “A
Computational Study of the Effect of False Vocal Folds
on Glottal Flow and Vocal Fold Vibration during Phona-
tion,” Annals of Biomedical Engineering, Vol. 37, No. 3,
2009, pp. 625-642. doi:10.1007/s10439-008-9630-9
[9] H. Hirose, “Clinical Aspects of Voice Disorders,” In-
teruna Publishers, Tokyo, 1998, p. 173.
[10] L. Li, H. Saigusa, Y. Nakazawa, T. Nakamura, T. Ko-
machi, S. Yamaguchi, A. Liu, Y. Sugisaki, E. Shinya and
H. Shen, “A Pathological Study of Bamboo Nodule of the
Vocal Fold,” Journal of Voice, Vol. 24, No. 6, 2010, pp.
738-741. doi:10.1016/j.jvoice.2009.06.003
[11] D. Wong, M. R. Ito and N. B. Cox, “Observation of Per-
turbations in a Lumped-Element Model of the Vocal
Folds with Application to Some Pathological Cases,”
Journal of the Acoustical Society of America, Vol. 89, No.
1, 1991, pp. 383-394. doi:10.1121/1.400472
[12] F. Alipour, D. A. Berry and I. R. Titze, “A Finite Element
Model of Vocal-Fold Vibration,” Journal of the Acousti-
cal Society of America, Vol. 108, No. 6, 2000, pp.
3003-3012. doi:10.1121/1.1324678
[13] I. R. Titze and T. Riede, “A Cervid Vocal Fold Model
Suggests Greater Glottal Efficiency in Calling at High
Frequencies,” PLoS Computational Biology, Vol. 6, No.
3, 2010, e1000897. doi:10.1371/journal.pcbi.1000897
[14] A. Yang, J. Lohscheller, D. A. Berry, S. Becker, U. Ey-
sholdt, D. Voigt and M. Döllinger, “Biomechanical Mod-
eling of the Three-Dimensional Aspects of Human Vocal
Fold Dynamics,” Journal of the Acoustical Society of
America, Vol. 127, No. 2, 2010, pp. 1014-1031.
doi:10.1121/1.3277165
[15] S. Deguchi and T. Hyakutake, “Theoretical Consideration
of the Flow Behavior in Oscillating Vocal Fold,” Journal
of Biomechanics, Vol. 42, No. 7, 2009, pp. 824-829.
doi:10.1016/j.jbiomech.2009.01.027
[16] S. Deguchi, “Mechanism of and Threshold Biomechani-
cal Conditions for Falsetto Voice Onset,” PLoS One, Vol.
6, No. 3, 2011, e17503.
doi:10.1371/journal.pone.0017503
[17] O. Fujimura, “Body-Cover Theory of the Vocal Fold and
Its Phonetic Implications,” In: K. Stevens and M. Hirano,
Eds., Vocal Fold Physiology, University of Tokyo Press,
Tokyo, 1981, pp. 271-288.
[18] M. Hirano, K. Kiyokawa and S. Kurita, “Laryngeal Mus-
cles and Glottic Shaping,” In: O. Fujimura, Ed., Vocal
Physiology, Mechanisms and Functions, Raven Press,
New York, 1988, pp. 49-65.
[19] I. R. Titze, J. J. Jiang and D. G. Druker, “Preliminaries to
the Body-Cover Theory of Pitch Control,” Journal of
Voice, Vol. 1, No. 4, 1988, pp. 314-319.
doi:10.1016/S0892-1997(88)80004-3
[20] I. R. Titze, E. S. Luschei and M. Hirano, “The Role of the

S. DEGUCHI ET AL.
201
Thyroarytenoid Muscle in Regulation of Fundamental
Frequency,” Journal of Voice, Vol. 3, No. 3, 1989, pp.
213-224. doi:10.1016/S0892-1997(89)80003-7
[21] S. Deguchi, Y. Kawahara and S. Takahashi, “Cooperative
Regulation of Vocal Fold Morphology and Stress by the
Cricothyroid and Thyroarytenoid Muscles,” Journal of
Voice, in press.
[22] T. Baer, J. C. Gore, L. C. Gracco and P. W. Nye, “Analy-
sis of Vocal Tract Shape and Dimensions Using Magnetic
Resonance Imaging: Vowels,” Journal of the Acoustical
Society of America, Vol. 90, No. 2, 1991, pp. 799-828.
doi:10.1121/1.401949
[23] G. R. Farley, “A Quantitative Model of Voice F0 Con-
trol,” Journal of the Acoustical Society of America, Vol.
95, No. 2, 1994, pp. 1017-1029.
doi:10.1121/1.408465
[24] T. Ikeda and Y. Matsuzaki, “A One-Dimensional Un-
steady Separable and Reattachable Flow Model for Col-
lapsible Tube-Flow Analysis,” Journal of Biomechanical
Engineering, Vol. 121, No. 2, 1999, pp. 153-159.
doi:10.1115/1.2835097
[25] S. Deguchi, Y. Miyake, Y. Tamura and S. Washio,
“Wavelike Motion of a Mechanical Vocal Fold Model at
the Onset of Self-Excited Oscillation,” Journal of Bio-
mechanical Science and Engineering, Vol. 1, No. 1, 2006,
pp. 246-255. doi:10.1299/jbse.1.246
[26] I. R. Titze, “The Physics of Small-Amplitude Oscillation
of the Vocal Folds,” Journal of the Acoustical Society of
America, Vol. 83, No. 4, 1988, pp. 1536-1552.
doi:10.1121/1.395910
[27] J. C. Lucero and L. L. Koenig, “On the Relation between
the Phonation Threshold Lung Pressure and the Oscilla-
tion Frequency of the Vocal Folds,” Journal of the
Acoustical Society of America, Vol. 121, No. 6, 2007, pp.
3280-3283. doi:10.1121/1.2722210