World Journal of Engineering and Technology
Vol.04 No.03(2016), Article ID:71331,8 pages
10.4236/wjet.2016.43D014
Design and Performance Evaluation of Piezo-Driven Synthetic Jet Devices
M. Chiatto, L. de Luca
Department of Industrial Engineering, Aerospace Sector, Università degli Studi di Napoli “Federico II”, Naples, Italy




Received: July 23, 2016; Accepted: October 13, 2016; Published: October 20, 2016
ABSTRACT
In the last two decades synthetic jet actuators have gained much interest among flow control techniques due to their short response time, high jet velocity and absence of traditional piping, that matches the requirements of reduced size and low weight. A synthetic jet is generated by the diaphragm oscillation (generally driven by a piezo- electric element) in a relatively small cavity, producing periodic cavity pressure variations associated to cavity volume changes. The high pressure air exhausts through an orifice, converting membrane elastic energy in jet kinetic energy. This review paper faces the development of various lumped-element models (LEM) as practical tools to design and manufacturing actuators. LEM can predict quickly device performances such as frequency response in terms of membrane displacement, cavity pressure and jet velocity, as well as efficiency of energy conversion of input Joule power into useful kinetic power of air jet. Actuator performance is analyzed also by varying typical geometric parameters such as cavity height and orifice diameter and length, through a proper dimensionless form of the governing equations.
Keywords:
Synthetic Jets, Flow Control, Lumped Element Model

1. Introduction
It has been many years since synthetic jet (SJ) actuators have been used for active flow control, particularly for aerospace applications. These devices are able to manipulate the flow, modify its structure and allow a favorable variation of the aerodynamic forces on aircrafts [1]-[3]. Their application field is extremely wide, including separation control, mixing enhancement, heat transfer from small surfaces, spray vectoring, and many others [4]-[8]. A synthetic jet, as depicted in Figure 1, is an electromechanical device which consists of a relatively small cavity, from one side sealed by an elastic vibrating
Figure 1. Sketch of a typical synthetic jet device driven by a piezoelectric element.
diaphragm and from the other one linked to the external environment through a slot or an orifice. The diaphragm (membrane, wall) oscillation, generally driven by a piezo- ceramic element, produces periodic cavity volume changes, with corresponding pressure variations, that cause subsequent alternation of ejection and suction phases of fluid across the orifice. During the expulsion phase, a vortex ring forms near the orifice exit which, under favorable operating conditions, convects downstream by its self-induced velocity towards the far field. Few cycles result in the formation of a train of vortex rings that interact and break up due to the viscous dissipation eventually “synthesizing” a turbulent jet always directed downstream. A major characteristic of this jet is that it exhibits a zero-net mass-flux during an operating cycle, but a non-zero momentum flux. Furthermore, it does not require a continuous supply of fluid for its generation, because it is synthesized directly from the surrounding fluid [9] [10].
Nowadays, synthetic jets have been extensively studied both from experimental and numerical points of view. Hot-wire anemometry, laser doppler velocimetry (LDV) and particle image velocimetry (PIV) are only some of the several measurement techniques applied to determine the flow field generated by these devises [11]. At the same time, several CFD simulations have been conducted, going from the first RANS to the very recent LES and DNS computations, to achieve further details of the flow fields inside the cavity as well as at the orifice, both in quiescent and cross-flow configurations [12] [13]. Another very useful approach, for design and manufacturing purposes, consists in the definition of a low-order model, able to predict the dynamic response of the actuator with reasonable fidelity and accuracy. Within this latter class, lumped element models (LEM) represent a very useful practical tool to provide the time variation of all thermodynamic variables inside the cavity as well as the jet velocity at the orifice, as functions of the operating frequency.
One of the earliest lumped model application to synthetic jets has been presented in [14], regarding a simple electroacoustic model to predict the velocity performance of a SJ actuator driven by an acoustic source. The extension of the previous model to piezoelectric-driven devices has been developed in [15] and extended in [16], where the individual components of the actuator are modeled as elements of an equivalent electrical circuit using conjugate power variables. The model was validated with experimental measurements of the orifice exit velocity. Following this electroacoustic approach, many other lumped models have been realized, introducing further considerations about the piezoelectric element, minor losses, electromagnetic driver and double cavity. Later on, an analytical model based on fluid dynamic equations has been presented in [17]. In this work the oscillating diaphragm is considered as a single-degree- of-freedom mechanical system, while the base cavity-orifice arrangement is described by proper forms of continuity and Bernoulli’s unsteady equations. This model inspired the work [18], which provides additional analytical and numerical insights on the frequency response of SJ actuators driven by piezoelectric thin elements. The work [20] deals with the efficiency of the energy conversion process. In conclusion, lumped element models regarding synthetic jets can be divided in two branches: one deals with an equivalent electrical circuit; the other one is fully based on fluid dynamics equations. In any case, the device can be considered as a coupled mechanical diaphragm-Helmholtz resonator system with two degrees of freedom, exhibiting two resonance frequencies near the uncoupled Helmholtz and diaphragm structural resonance frequencies.
The aim of this work is to present a lumped element model (LEM) able to predict the device performances as function of its main dimensionless parameters.
2. Lumped Element Models
A lumped element model (LEM) is a low order model which, under certain assumptions, allows to describe the behavior of a physical system through a finite number of elements (lumped elements) properly connected to each other. This simplification decouples temporal and spatial variations, reducing the partial differential equations of the distributed system into a set of coupled ordinary differential equations. It is a practical tool for design and manufacturing intents, providing the dynamic response of a complex system in a very short computation time with a high level of accuracy.
In lumped models it is assumed that the characteristic length scales of the governing phenomena are much greater than the larger geometric dimension of the system. Considering, for instance, the cavity flow which undergoes alternate compression and expansion phases due to the wall oscillations, the internal pressure can be considered uniform at any given time instant if the wavelength of the pressure oscillations is much larger than a typical dimension of the actuator cavity, [17]. Accordingly, the lumped assumption may become invalid at very high frequencies.
A synthetic jet actuator model directly based on the laws of fluid mechanics was presented in [17] and extended in [18] [19]. The model is able to predict cavity pressure fluctuations, phase relationships between different variables, as well as exit velocity exit at the orifice. It is necessary to model the three basic elements of the actuator: the oscillating diaphragm, the cavity and the orifice.
With the aim of providing further insights to the problem physics, the governing equations can be recast into a convenient dimensionless form [20]. A physical inspection yields the determination of the dimensionless parameters reported in Table 1.
Table 1. Main dimensionless variables of the problem.
These variables include some geometrical ratios, the standard Reynolds (Re), Stokes (S) and Strouhal (St) numbers, the ratio between the air mass inside the cavity and the total mass, and the so called coupling factor (CF) defined as the ratio of the air stiffness to the membrane stiffness. ωw is the membrane natural frequency and ω the operation frequency. The variation of one of these parameters affects the actuator response.
The dimensionless process relies on the choice of proper reference quantities for time, length and velocity; in this case, they are the reciprocal of the operating frequency 1/ω, the cavity height H and the air speed of sound c, respectively. According to [20], the non-dimensional form of the dynamics equation of the acoustic oscillator is:
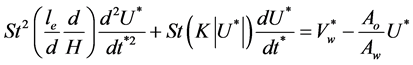 (1)
(1)
Note that the Strouhal number can be re-written by introducing the Helmholtz frequency ωH:
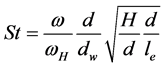 (2)
(2)
The St << 1 condition represents the case of acoustically thin cavity, for which the travelling time of a small pressure disturbance, over the distance H, is much smaller than the reference time 1/ω. From an operative point of view, this means that the air inside the cavity behaves as an incompressible medium (i.e., the air stiffness is infinite). The Equation (1), in this case, reduces to the dimensional relationship:
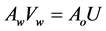 (3)
(3)
This means that the volume rate entering the cavity, as a consequence of the membrane displacement, equals the volume rate of air expelled through the orifice. On the other hand, the membrane dynamics is decoupled from that of the acoustic oscillator, with the membrane being driven by the piezo-electric forcing only. When St<<1, once the air velocity at the orifice has been obtained from Equation (3), the cavity pressure may be evaluated by using the unsteady form of the Bernoulli's equation, [18].
Another relevant conditions happens for St>>1, which also corresponds to decoupled membrane dynamics. For this case, the air stiffness is vanishing, the pressure field inside the cavity is practically unperturbed, therefore the air jet velocity U is vanishing too. It worth noting that for this condition the lumped assumption is invalid, hence it is not considered for the device performance evaluation (Section 3).
Another relevant equation of the problem is the motion equation of the diaphragm which, in its non-dimensional form, is:
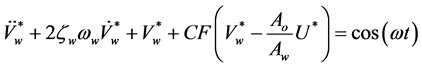 (4)
(4)
Note that under the condition CF<<1 (which means that the air stiffness is negligible in comparison with the membrane stiffness) the membrane dynamics is decoupled from the acoustic oscillator one. In this case the jet velocity and the cavity pressure are determined via the continuity and the unsteady Bernoulli's equations. Furthermore, the modified structural and Helmholtz’s frequencies tend to coincide with the corresponding uncoupled frequencies.
3. Performances
The aim of this section is to provide a deep investigation of the device performances varying the main dimensionless parameters defined in Table 2. For sake of clarity, all results have been referred to the same technology, namely the piezoelectric actuators presented in [20]. Two different actuators, named “Aluminum 1” and “Aluminum 2” have been manufactured and analysed. For the former is CF = 0.34, for the latter CF = 1.38.
Numerical simulations have been carried out by integrating numerically the governing Equations [18], through a standard 4th order Runge-Kutta method in MATLAB environment with ode45 routine. Initial conditions of xw = 0, 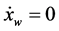 , pi = 0 and U = 0 have been assumed for all the computations. Typical values of the electroacoustic transduction coefficient, the only fitting parameters of the model, Φa are 110 and 83 for Aluminum 1 and Aluminum 2, respectively.
, pi = 0 and U = 0 have been assumed for all the computations. Typical values of the electroacoustic transduction coefficient, the only fitting parameters of the model, Φa are 110 and 83 for Aluminum 1 and Aluminum 2, respectively.
3.1. Effect of the Coupling Factor
The coupling factor, CF, has been introduced above. From Equation (4), one can observe that when CF << 1, the membrane dynamics is decoupled from the acoustic oscillator one. In this case, the jet velocity and the cavity pressure are determined via the continuity and the unsteady Bernoulli’s equations; the modified and Helmholtz’s frequencies tend to coincide with the uncoupled frequencies. Note that, for CF << 1 the two resonance frequencies tend to those of the uncoupled oscillators.
To better understand the effect of this parameter, it is convenient to consider the characteristic frequencies of the devices, reported in Table 2. For the sake of clarity, it is remembered that fw and fH denote the (uncoupled) first-mode structural and Helmholtz natural frequencies; f1 and f2 are the frequencies of the two coupled oscillators, i.e., the modified first-mode structural and Helmholtz resonance frequencies, numerically computed; and f1d and f2d take into account linear damping effects and arise from an eigenvalues problem, [18].
Table 2. Characteristic frequencies of the devices, extracted from [20].
As shown in Table 2, the natural frequencies of the Aluminum 1 device are closer to the values predicted by the model of the coupled oscillators than the Aluminum 2 case. This is true evaluating the coupling frequencies both including damping effects (acting on the mechanical oscillator) and neglecting them; in fact, it is possible to find also that f1 ≅ f1d and f2 ≅ f2d. As a general trend, the coupling effect increases the structural resonance frequency and lowers the Helmholtz resonance frequency. However, because for the Aluminum 2 device the nominal structural frequency is less than the Helmholtz one, the situation is reversed in the sense that the coupling of the oscillators lowers f1 and f1d and raises f2 and f2d.
3.2. Effect of Strouhal Number
The effect of the Strouhal number can be appreciated by focusing the attention on the cavity height variation. The maximum jet flow exit velocity trends, for the two tested devices, as functions of the operating frequency are depicted in Figure 2, for various dimensionless cavity heights, H/d. The supply voltage Vac is equal to 35 V in all simulations.
For all devices the two velocity peaks corresponding to the two resonance frequencies are clearly evident. For the Aluminum 1 device the trend is that the velocity peak of the structural resonance reaches a plateau for intermediate values of H/d and then it decreases at the largest height. Furthermore, the distance between the two resonance frequencies slightly decreases. Note that the experimental findings, as reported in [20] show also that the resonance frequencies distance becomes practically constant as H/d further increases, in agreement with the analytical prediction, presented in [18], valid in the case of ωw >> ωH.
The straight lines present in the plots of Figure 2 refer to the linear dependence of the jet velocity upon the operating frequency given by the incompressible model described by the Equation (3). For all actuators it is clearly evident that such a simplified model closely agrees with the simulations of the complete model at relatively low frequencies, with the frequencies range of such an agreement widening for the smaller cavity heights, as predicted by the theory for St << 1. Note also that for this range of
Figure 2. Frequency response of the average exit flow velocity for Aluminum 1 (left) and Aluminum 2 (right) actuators for different voltages cavity height; black dotted line is for H/d = 0.5, magenta dash-dotted line H/d = 1, blue dashed line H/d = 1.5, red solid line H/d = 2.5. The straight line refers to Equation (3). Voltage is 35 V.
frequencies the response in terms of jet velocity is the same whatever is the cavity height, thus confirming that the membrane dynamics is decoupled from the acoustic oscillator one.
In order to complete the discussion about the behavior of the Aluminum 2 device, note that the two nominal Helmholtz and structural frequencies, which for this actuator are reversed, are remarkably modified by the high coupling ratio. The jet velocity decreases with increasing the cavity height at the structural resonance frequency, whereas it increases with increasing H/d at the Helmholtz resonance frequency, with the result that the maximum peak is reached at the Helmholtz frequency for the highest simulated cavity height. This particular finding agrees, again, with the theoretical prediction presented in [18]. The quasi-coincidence of the two resonance frequencies justifies that the maximum peak is reached for the highest cavity height. It is interesting to note that this result has been confirmed also experimentally also for the case of a loudspeaker driven synthetic jet actuator, as discussed in [21].
4. Conclusions
Synthetic jet actuators represent a valuable technology for active flow control problems. Their capability to manipulate the flow, modify its structure and improve aircraft aerodynamic performances has allowed them to gain much interest in the scientific community.
After a short introduction recalling the basic principles of the device, the characteristic non-dimensional groups of the problem have been presented. Then, the basic actuator performances have been reported, essentially as functions of the main dimensionless parameters.
Cite this paper
Chiatto, M. and de Luca, L. (2016) Design and Performance Eva- luation of Piezo-Driven Synthetic Jet Devices. World Journal of Engineering and Techno- logy, 4, 107-114. http://dx.doi.org/10.4236/wjet.2016.43D014
References
- 1. Glezer, A. and Amitay, M. (2002) Synthetic Jets. Annu. Rev. Fluid Mech., 34, 503-529. http://dx.doi.org/10.1146/annurev.fluid.34.090501.094913
- 2. Cattafesta III, L.N. and Sheplak, M. (2010) Actuators for Active Flow Con-trol. Annu. Rev. Fluid Mech., 43, 247-272. http://dx.doi.org/10.1146/annurev-fluid-122109-160634
- 3. Smith, B.L. and Glezer, A. (2002) Jet Vectoring Using Synthetic Jets. J. Fluid Mech., 458, 1-34. http://dx.doi.org/10.1017/S0022112001007406
- 4. Glezer, A. (2010) Some Aspects of Aerodynamic Flow Control Using Synthetic-Jet Actuation. Phil. Trans. R. Soc. A, 369, 1476-1494. http://dx.doi.org/10.1098/rsta.2010.0374
- 5. Wang, H. and Menon, S. (2001) Fuel-Air Mixing Enhancement by Synthetic Microjets. AIAA Journal, 39, 2308-2319. http://dx.doi.org/10.2514/2.1236
- 6. Chaudhari, M., Puranik, B. and Agrawal, A. (2010) Heat Transfer Characte-ristics of Synthetic Jet Impingement Cooling. Int. J. Heat and Mass Transfer, 53, 1057-1069. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2009.11.005
- 7. Pavlova, A.A., Otani, K. and Amitay, M. (2007) Active Control of Sprays Using a Single Synthetic Jet Actuator. Int J. Heat and Fluid Flow, 29,131-148. http://dx.doi.org/10.1016/j.ijheatfluidflow.2007.06.004
- 8. Marchitto, L., Valentino, G., Chiatto, M. and de Luca, L. (2016) Experimental Characterization of Spray Water Controlled by a Synthetic Jet. Proceedings of 18th International Symposium on the Application of Laser and Imaging Techniques to Fluid Mechanics, Lisbon, 4-7 July 2016.
- 9. Smith, B.L. and Glezer, A. (1998) The Formation and the Evolution of Synthetic Jets. Physics of Fluids, 10, 2281-2297. http://dx.doi.org/10.1063/1.869828
- 10. Cater, J.E. and Soria, J. (2002) The Evolution of Round Zero-Net-Mass-Flux Jets. J. Fluid Mech., 472, 167-200. http://dx.doi.org/10.1017/S0022112002002264
- 11. Mohseni, K. and Mittal, R. (2015) Synthetic Jets: Fundamentals and Applications. CRC Press-Taylor & Francis Group LCC, Abingdon.
- 12. Rumsey, C.L., Gatski, T.B., Sellers III, W.L., Vatsa, V.N. and Viken, S.A. (2006) Summary of the 2004 Computational Fluid Dynamics Validation Workshop on Synthetic Jets. AIAA Journal, 44, 194-207. http://dx.doi.org/10.2514/1.12957
- 13. Dandois, J., Garnier, E. and Sagaut, P. (2007) Numerical Simulation of Active Separation Control by a Synthetic Jet. J. Fluid Mech., 574, 25-58. http://dx.doi.org/10.1017/S0022112006003995
- 14. McCormick, D.C. (2000) Boundary Layer Separation Control with Directed Synthetic Jets. Proceedings of 38th Aerospace Sciences Meeting and Exhibit, 10-13 January 2000, 2000- 0519. http://dx.doi.org/10.2514/6.2000-519
- 15. Prasad, S.A.N. (2002) Two-Port Electroacoustic Model of Piezoelectric Composite Circular Plate. M.S. Thesis, Dept. of Aerospace Engineering, Mechanics and Engineering Sciences, University of Florida, Gainsville.
- 16. Gallas, Q., Holman, R., Nishida, T., Carroll, B., Sheplak, M. and Cattafesta III, L. (2003) Lumped Element Modeling of Piezoelectric-Driven Synthetic Jet Actuators. AIAA Journal, 41, 240-247. http://dx.doi.org/10.2514/2.1936
- 17. Sharma, R.N. (2007) Fluid-Dynamic-Based Analytical Model for Synthetic Jet Actuation. AIAA Journal, 45, 1841-1847. http://dx.doi.org/10.2514/1.25427
- 18. de Luca, L., Girfoglio, M. and Coppola, G. (2014) Modeling and Experimental Validation of the Frequency Response of Synthetic Jet Actuators. AIAA Journal, 52, 1733-1748. http://dx.doi.org/10.2514/1.J052674
- 19. Girfoglio, M., Greco, C.S., Chiatto, M. and de Luca, L. (2015) Modelling of Efficiency of Synthetic Jet Actuators. Sensors and Actuators A: Physical, 233, 512-521. http://dx.doi.org/10.1016/j.sna.2015.07.030
- 20. de Luca, L, Girfoglio, M., Chiatto, M. and Coppola, G. (2016) Scaling Properties of Reso-nant Cavities Driven by Piezo-Electric Actuators. Sensors and Actuators A: Physical, 247, 465-474. http://dx.doi.org/10.1016/j.sna.2016.06.016
- 21. Gil, P. and Strzelczyk, P. (2016) Performance and Efficiency of Loudspeaker Driven Syn-thetic Jet Actuator. Experimental Thermal and Fluid Science, 76, 163-174. http://dx.doi.org/10.1016/j.expthermflusci.2016.03.020





