ABSTRACT

Electricity price forecasting has become an important aspect of promoting competition and safeguarding the interests of participants in electricity market. As market participants, both producers and consumers intent to contribute more efforts on developing appropriate price forecasting scheme to maximize their profits. This paper introduces a time series method developed by Box-Jenkins that applies autoregressive integrated moving average (ARIMA) model to address a best-fitted time-domain model based on a time series of historical price data. Using the model’s parameters determined from the stationarized time series of prices, the price forecasts in UK electricity market for 1 step ahead are estimated in the next day and the next week. The most suitable models are selected for them separately after comparing their prediction outcomes. The data of historical prices are obtained from UK three-month Reference Price Data from April 1^st to July7^th 2010.

Keywords:

Box-Jenkins Method, ARIMA Models, Electricity Markets, Electricity Prices, Forecasting

1. Introduction

Worldwide electricity market reform makes the power industry transform from gradually monopoly to competition. As market participants, each supplier and consumer wants to get the most benefits [1]. If the electricity price can be predicted accurately, generation side could handle the market dynamic and make optimal power generation plan. Demand side could select their time of power use and choose the electric quantity they want to buy for reducing the cost and increasing market competitiveness [2]. For regulators, grid reference price forecast results can help to improve the monitoring capability of electricity market operation and discover and resolve the problems in the market. Also, government can formulate related policies by electricity prices and guide electricity market development [3].

Many electricity price forecasting methods have been proposed, and they generally can be divided into market simulation and the method centred on history data. Market simulation predicts the market clearing prices by simulating the competition operation. The second kind of method based on time series analysis of history data to build mathematical model and make the prices forecasting [4]. Box-Jenkins method belongs to the time-series model. Box-Jenkins Analysis refers to a systematic method of identifying, fitting, checking, and using autoregressive integrated moving average (ARIMA) time series models.

In the late 1980s, UK took the lead in implementing industry privatization reform and proposed deregulation of the electricity power supply industry. The deregulated Scottish electricity market was formed in 1998 and the whole of the UK market was formed two years later. All customers in the market can choose their power suppliers freely [5]. On 27 March 2001, the market introduced new market mechanisms and trading patterns in England and Wales, the New Electricity Trading Arrangements (NETA) and was later extended to cover the whole of the UK (BETTA) [6].

2. Box-Jenkins Methodology

2.1. Autoregressive Integrated Moving Average (ARIMA) Models

ARIMA model is a time-series forecasting method which was proposed by Box and Jenkins in the early 1970s [7].ARIMA model contains three factors, p, d and q. AR is autoregressive (p), MA is moving average (q) and d is the level of differencing to stationarize the time series. The formula of the ARIMA model is:

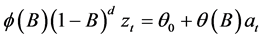(1)

where 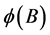is the operator of p and 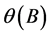is the operator of q. Their zeros need to be outside the unit circle. B is the lag operator, 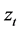is the historical data at time t and 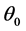is the constant term. The error term is generally assumed to be independent and its average value is zero [8].

Electricity prices are highly non-stationary time series of strong volatility and periodicity. A time series based forecasting model is usually carried out for the analysis and prediction of stationary series. Therefore, it is necessary to transfer the electricity price to a stationary time series, which is termed the pre-treatment process. Differencing is the major approach to convert time series form non-stationarity to stationarity. Provided the electricity price series are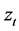, 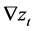is the first order difference of is the d^th order difference of:

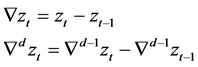(2)

Usually when the value of d is up to 2, the differenced time series could become stationary. There are a number of methods to detect the stationarity of the differenced time series [9]. In this paper, the model’s residuals are used to verify the goodness of fit. The modelling process can then be carried out.

Using the stationsrized time series, the ARIMA process may be simplified to the mixed autoregressive moving average (ARMA) process:

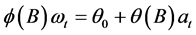(3)

where

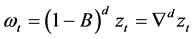(4)

It also can be expressed as:

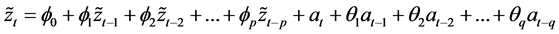(5)

The autoregressive (AR) part is a linear combination of the past p observations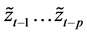, weighted by plinear coefficients 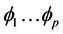and a constant term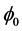. The moving average (MA) part is a linear combination of the past q linear coefficients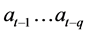, weighted by q linear coefficients, and the current noise term . Based on the central limit theorem, the noise terms are normally distributed with mean zero and constant variance [10].

The main tool used to identify the resulting ARMA model is the sample autocorrelation function (ACF) and the sample partial autocorrelation function (PACF). Table 1 summarizes standard patterns and provides guidelines for determining the integers p and q, identifying the most influential p observations and q noise terms in an ARMA (p, q) model [11].

2.2. Autocorrelations and Partial Autocorrelations Models

Autocorrelations (AC) reflect the linear dependencies among every sequential value, in the electricity price sequence. and, separated by time lags k = 1, 2, ….The autocorrelation coefficient at lag k figures out the average variation associated with the sample mean normalized by the sample variance, of all pairs separated by k lags. Hence, at lag k of the electricity price series of size N is:

(6)

The range of autocorrelation coefficient is [−1, 1] and the magnitude represents the intensity of dependency. The more is close to 1, the higher correlation intensity of the series.

For the price time series, under the given situation the partial autocorrelation (PAC) measures the degree of association between two random variables and. The partial autocorrelation of the price time series is

(7)

where is the autocorrelation coefficient of price series at lag k.

(8)

The range of partial autocorrelation coefficient is also [−1, 1]. In practical applications, it is necessary to consider both autocorrelations and partial autocorrelations of the time series [12].

2.3. The Procedure of ARIMA Modelling

The half-hourly updated UK Reference Price Data (RPD) over 91 days from April 1^st to June 30^th 2010were obtained from Power Spot Exchange (www.apxgroup.com). The objective is to predict the 1-step-ahead price forecast in the next day (July 1^st) and next week (from July 1^st to 7^th).

There are five steps to complete the ARIMA modelling:

1. Stationarize the time series.

2. Identify the model based on the observed data.

3. Determine the parameters of the model.

4. Check the goodness of fit.

5. Use the tested model to do the forecasting [13].

3. Results and Discussion

The parameters of the ARIMA models are determined from the historical price data over three months (April, May and June 2010). The price forecasts for 1 step ahead in the next day on July 1^st produced by the ARIMA(1,1,1) and the next week from July 1^st to July 7^th produced by the ARIMA(1,1,1) are compared with their actual price values as shown in Figure 1 and Figure 2 respectively. The dashed lines representing the actual values and the solid lines representing the forecasts are well covered by each other which indicate good forecasting performances are achieved in both figures.

Mean absolute error (MAE) and root-mean-square error (RMSE) [14] are used to characterise the differences between predicted values and observed values. The formulas are given by:

(9)

where is the predicted value, is the observed value and n is the number of testing samples. The MAEs and RMSEs of price forecasts in the next day and the next week produced by different ARIMA models are shown in Table 2 and Table 3 respectively.

The ARIMA (1,1,1) model are generally shown to generate the 1-step-ahead price forecasts of the minimum MAEs and RMSEs in Table 2 and Table 3. In order to check the quality of the forecasting model, the MAEs and RMSEs of ARIMA (1,1,1) model are compared with the ones given by persistence forecasting. Persistence forecasting (PF) is the simplest form of short-term forecasting which assumes the forecast value at T time ahead equal to the current value [15]. The persistence forecast error is used here as a benchmark for the ARIMA (1,1,1) model.

Table 4 compares the MAEs and RMSEs of 1-step-ahead and 3-steps-ahead forecasts on July 1^st 2010 and during the week from July 1^st to July 7^th 2010for the ARIMA (1,1,1) model and persistence forecasting.

It can be observed that both MAEs and RMSEs of the ARIMA (1,1,1) model are smaller than PF. Especially for the price forecasts during the week, the MAE and RMSE of PF reached 4.58 and 6.50 respectively, which are much bigger than that of the ARIMA (1,1,1) model.

4. Conclusions and Future Work

This paper has proposed an ARIMA model for the1-step-ahead electricity price forecasting based on historical price data in UK electricity market. Depending on the forecast accuracy in terms of MAE and RMSE, an appropriate forecasting model has been selected. Every component of the modelling process could affect the forecasts. Furthermore, to raise the accuracy of forecasting results, increasing the historical data and making short-time prediction are effective. But if the historical data is increased beyond a certain quantity, the accuracy will increase very slowly after a certain value.

The selected ARIMA (1,1,1) model is shown to have a reasonably satisfactory forecasting performance. The errors of persistence forecasts are additionally estimated as a benchmark over which the ARIMA (1,1,1) model gives a significant improvement in both MAE and RMSE.

Future work will continue to refine the optimal models for predicting electricity price and build a rolling forecasting process in electricity market to achieve more accurate results step-by-step. Alternatively, other statistical models, e.g., an artificial neural network (ANN) model or an AR model combined with trend modelling [16] will be established and their forecast accuracies will be compared with the ARIMA models. The optimum models will be employed to generate the electricity price forecasts of high reliability and accuracy.

Acknowledgements

The authors would like to thank Power Spot Exchange for supplying UK historical electricity prices.

Cite this paper

Gao, G., Lo, K., Lu, J.F. and Fan, F.L. (2016) A Short-Term Elec- tricity Price Forecasting Scheme for Power Market. World Journal of Engineering and Technology, 4, 58-65. http://dx.doi.org/10.4236/wjet.2016.43D008

References