Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70963,7 pages
10.4236/opj.2016.68B037
A New Pulse Delta-Sigma CO2 NDIR Gas Detector
Steven Z. Y. Shen, Chi-Feng Chen, Hilbert C. S. Shen
Department of Optics and Photonics, National Central University, Taiwan



Received 30 May 2016; accepted 23 August 2016; published 30 August 2016

ABSTRACT
This work describes the implementation and the modeling of an infrared gas sensor with pulse delta-sigma sensing architecture. Beyond the conventional technique of constant periodic heating of infrared light source, our proposed delta-sigma architecture with closed-loop feedback system is built with the hybrid combination of a CO2 infrared sensor with a specific wavelength filter, an infrared MEMS heater, a chopper amplifier, threshold comparator, ARM based MPU and discrete electronic devices. After a modeling of system, we built a model for the description of relationship between gas concentration and sensor by the duty of heating. The measurement results show a good linear behavior of signal and it proves to be a practical for all the NDIR measuring techniques and this work also gives a new approach not only to measure gas concentration fast but also obtain the high resolution.
Keywords:
Carbon Dioxide, Delta-Sigma, Gas Sensor, NDIR, Sensitivity

1. Introduction
Nowadays, technology changes for the better day by day, and month by month. It makes our quality of life better and better. However, we also bring our environment more and more destruction, like global warming. According to the advisement of the American Society of Heating Refrigerating and Air-Conditioning Engineers (ASHRAE), while CO2 (Carbon dioxide)concentration in 300 ppm to 400 ppm, we feel convenient, but it is dangerous when CO2 concentration is more than 5000 ppm.
Presently, gas concentration is divided into two types. First type is using NDIR (non-dispersive infrared sensor) [1] method, and second is using chemical method. The NDIR method is a physical method, which have high sensitivity, long-term stability and do not pollute environment.
Normally, we use the NDIR technique in a light source [2] which is heated periodically without controlling temperature that tends to an unstable signal. In order to solve this problem, we combine delta-sigma architecture [3] [4] with NDIR-based system and using a feedback loop to surmount the problem of offset which is infrared radiation intensity. Furthermore, we modulate gain and reference voltage of comparator for changing sensitivity of the measuring instrument. Therefore, we not only solve drift problem but also have high resolution measuring instrument.
2. Theory and Modelling
2.1. Beer-Lambert’s Law Using in NDIR Technique
The NDIR which working principle is based on the Beer-Lambert’s Law that describes the rate of absorption of infrared radiation by gas concentration (C) and absorb length (d). When the infrared light pass through thepath with gas and usually a gas chamber with low emissivity is used as the detection optical path. During the path, the gas will absorb a certain amount of infrared radiation energy which is irradiated from an infrared light source. Therefore, as the received infrared light intensity (I) decreases, the signal level of infrared detector also goes low. This principle can be expressed:
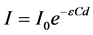 (1)
(1)
where Io is the initial intensity of the infrared light before entering the gas chamber, and d is the length of the well-controlled gas chamber, and ε is the coefficient of the absorption of the gas.
2.2. Proposed Delta-Sigma Architecture for NDIR Sensing
A delta-sigma architecture based on digital modulation of heating is built for CO2 NDIR sensing in this work. The conventional NDIR gas sensing technique is proceeded with a constant periodic heating of infrared light source which provides the incoming infrared radiation to the optical chamber and the decay of received infrared signal corresponds to the gas concentration. After an enough period of heating time, the temperature of light source will reach a stable working point and it means that the detection of gas concentration is available. Nevertheless, the principle of detection is based on a stable incoming infrared radiation, and the signal of infrared sensor goes low as the gas concentration rises. The drawback of the conventional technique shows a non-linear characteristic response curve which is caused from the exponential behavior of the Beer Lambert’s law and the biquadratic Stefan-Boltzmann’s law. It also shows a worse resolution of gas concentration.
We proposed a delta-sigma architecture with feedback loop which gives a novel linear transfer function between the gas concentration and the infrared signal intensity. The feedback loop is built based on the received intensity of infrared sensor during the heating cycle. Once the received signal intensity rises across a pre-set threshold level, the output of a comparator will change from low to high. The output signal is delivered to an ARM based microprocessor which controls a Power-PMOS and the switch on and off is decided by our proposed Delta-Sigma algorithm. The proposed algorithm gives a ratio value of heating numbers and total sampling numbers which shows a linear relationship with the gas concentration.
2.3. Theory
According to the above concept, we have built a new theoretical model for the delta-sigma on NDIR gas detection. For the total count of sampling is denoted as N. The number of heating count is denoted as m. Furthermore, the sampling time is denoted as ∆t. Such structure is shown in Figure 3.
Fixing the concentration of the gas, according to heat transfer theory, we can conclude that the temperature of the infrared light (T(t+Δt)) is equal to the initial temperature of the infrared light (T(t)) plus rising temperature (∆T) plus losing temperature (∆Td). Therefore, the heating power of a circuit with infrared light can be expressed in
Figure 1. Schematic diagram of beer-Lambert’s law.
Figure 2. Proposed Delta-Sigma architecture with close loop for NDIR.
Figure 3. The series of over-sampling cycles for heating and cooling of the heater.
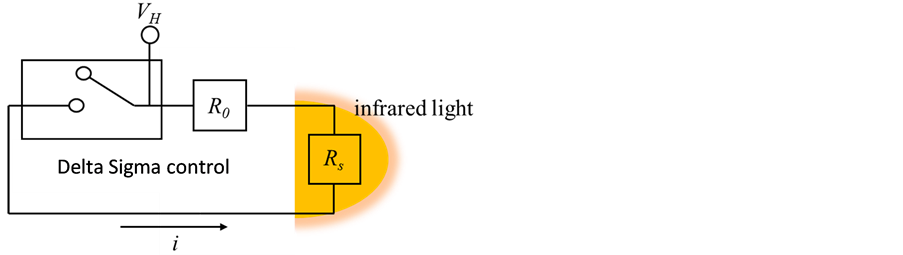
Equation (2). The input voltage of the circuit is denoted as VH. The amount of the current is denoted as i. The resistance of the outside circuit is denoted as R0. The resistance of the infrared light’s filament is denoted as Rs. Such structure is shown in Figure 4.
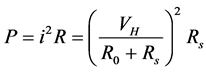 (2)
(2)
The heat which is absorbed by the filament is denoted as Q. The heat capacity coefficient is denoted as H. According to Q, we can derive the heating temperature of the filament (∆T).
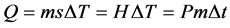 (3)
(3)
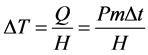 (4)
(4)
Using the heat lost formulation of the heat transfer theory, the radiating power is denoted as Pd. The coefficient of heat conduction is denoted as G. The temperature of the filament is denoted as Tb. The room temperature is denoted as Ta. The formulation is show in Equation (5).
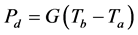 (5)
(5)
The radiating heat of the filament is denoted as Qd, and the formulation of the radiating temperature expresses:
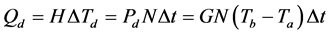 (6)
(6)
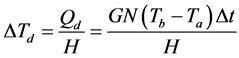 (7)
(7)
Concluding all the formulation above, we can derive the situation that filament is variation by temperature, and the formulation expresses:
Figure 4. Schematic diagram of the driving circuit for the heater.
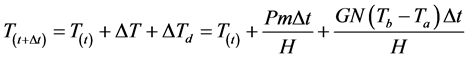 (8)
(8)
When the temperature is thermal equilibrium, the heating temperature will be equal to radiating temperature.
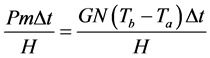 (9)
(9)
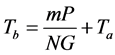 (10)
(10)
According to Stefan-Boltzmann’s Law, the total power of the radiation per time (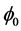 ) is proportional to the fourth power of the temperature (T). The emission rate of the body surface is denoted as A. The Stefan-Boltzmann proportionality constant is denoted as
) is proportional to the fourth power of the temperature (T). The emission rate of the body surface is denoted as A. The Stefan-Boltzmann proportionality constant is denoted as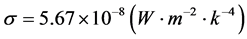 . The formulation is expressed in Equation (11).
. The formulation is expressed in Equation (11).
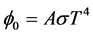
Basically, the NDIR working principle is based on the Beer-Lambert Law. Using that the light intensity, which is the radiation of the infrared light, is equal to the total power of the radiation per time. Therefore, we derive the Equation (12).
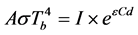
Finally, from Equation (10) and Equation (12) we can derive Equation (13). Equation (13) shows that the concentration of the gas, which is denoted as C, is a complex function of the ratio of the number of heating mand the total sampling number N.A reading parameter, heating ratio is defined as m/N which plays an important parameter of our proposed delta-sigma architecture.
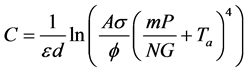
3. Results and Experiment
Verification of Theory
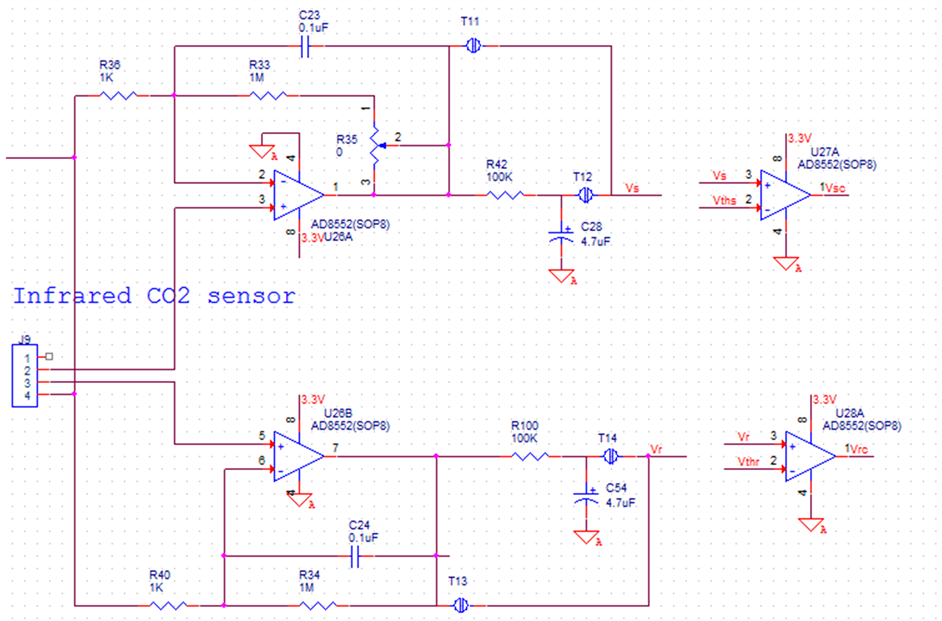
In order to investigate the relationship between CO2 concentration and heating times, a dual chopper amplifier is adopted. Then, after the amplification, signal is delivered to a comparator with a threshold voltage roughly at 0.4 V, shown in Figure 5. In this experiment, a reading of the concentration is controlled by counting in ARM, which shows an one-bit delta-sigma architecture to feedback the infrared light source.
First, the threshold voltage of the comparator is fixed at 0.4 voltage, and the gain of the sensor signal is 800.
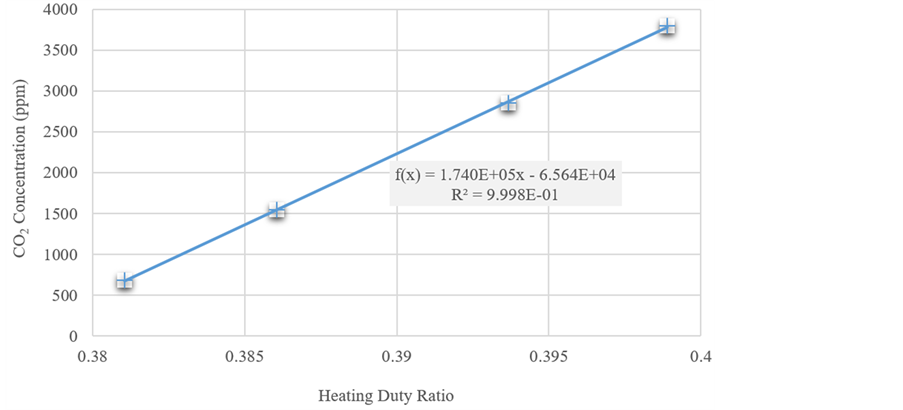
Under the gain of the sensor signal is 800 times, several gas concentration of 687 ppm, 1546 ppm, 2850 ppm, and 3800 ppm carbon dioxide are under test, and the corresponding counts are measured and recorded. Figure 6 shows a behavior of linear function between heating duty ratio and gas concentration which is built by our calibration systembased on a standard CO2 meter TES-1370.
Figure 5. Amplification of infrared sensor and comparison with threshold voltage.
Figure 6. CO2 concentration vs. heating ratio (m/N).
With comparing the formulation and experiment between heating duty ratio and CO2 concentration, we obtain consistent results and verify that delta-sigma theory for NDIR technique.
With further discussion, the relationship between different threshold voltage, sampling time, and temperature are under thorough investigation. The resolution is defined as the variation of CO2 concentration divided by the variation of heating times.
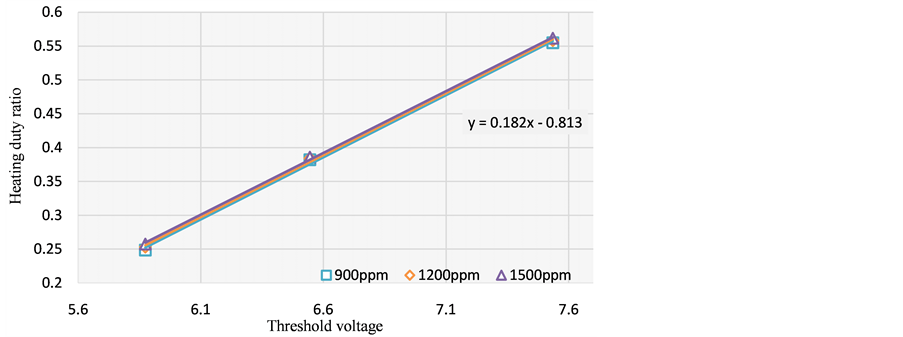
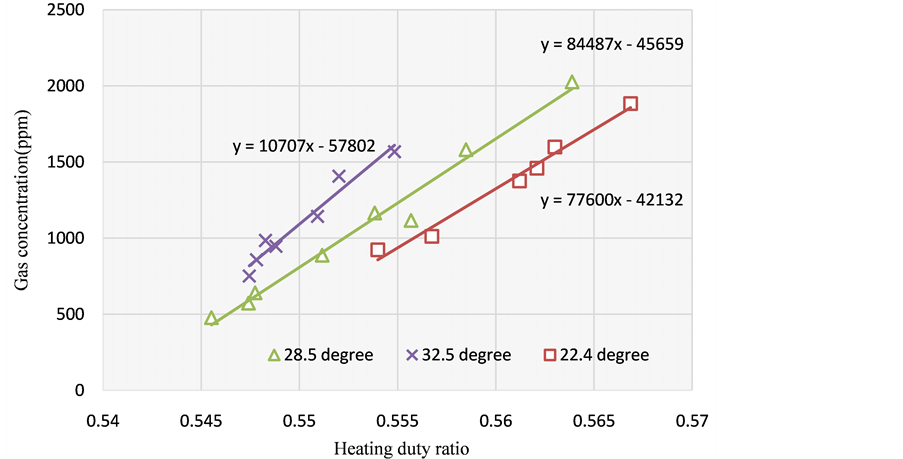
There are several factors influencing the detection. The first one we analyzed is the threshold voltage. When the threshold voltage becomes higher, the delta-sigma architecture will control the light and increase the radiation power to make the output voltage reach the new threshold value. Therefore, a higher heating ratio will be obtained. Figure 7 shows the experimental results under different threshold voltage. By observing these results, one can find that as the the threshold voltage increases, the higher the heating ratio will get higher under the same gas concentration. The experimental results are agreed with theoretical prediction.
The next interesting factor of our proposed measuring system is the sampling time. Since the transfer ratio of the radiation to the out power will increase or decay exponentially during the sampling time, the detected ratio will vary as long as the sampling time increases. Then, the relationship of the heating duty ratio and the gas concentration will change corresponding to different threshold voltage.
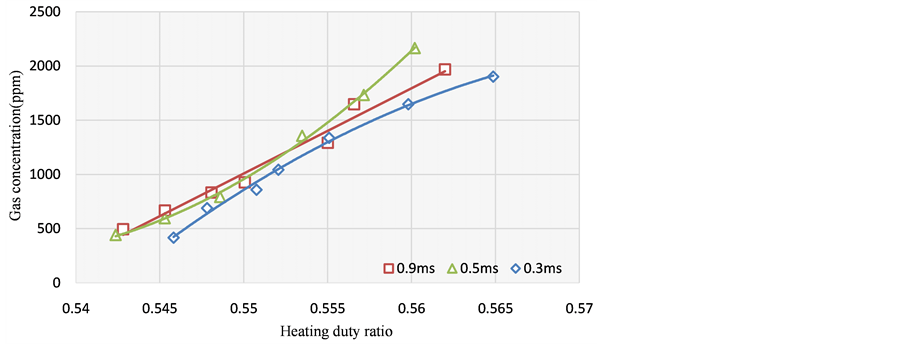
Figure 8 shows the experimental results under different sampling time. By observing these results, we can find out that the linearity of measuring curves show a great dependence on the sampling time. It means one can choose an appropriate sampling time to reach a good linearity of response.
The final important factor we focus is the ambient temperature. When the ambient temperature becomes higher, the thermopile sensor will transfer less heat to the circumstance, and it causes the output voltage becomes more close to the threshold voltage. It means we will get less output voltage drop of signal for less infrared radiation exchange and heat dissipation. In order to make the output voltage the same as the threshold value, as the increase of ambient temperature the control of delta-sigma architecture will make the heating ratio decrease. Figure 9 shows the experimental results under different ambient temperatures. By observing these results, the theoretical prediction also has a good agreement with experimental results.
It’s a significant factor since the ambient temperature is a natural environment factor without control for most of the practical application. These results also show an important issue that it needs more ambient compensation to reduce the measuring errors from the variation of environment.
Figure 7. The experimental curve under different threshold voltage.
Figure 8. The experimental curve under different sampling time.
Figure 9. The experimental curve under different temperature.
4. Conclusion
In this research, a delta-sigma architecture based on digital modulation of heating is built for CO2 NDIR sensing. The proposed a delta-sigma architecture with feedback loop which gives a novel linear transfer function between the gas concentration and the measuring signal. The feedback loop is built based on the received intensity of infrared sensor during the heating cycle. Once the received signal intensity rises across a pre-set threshold level, a decision circuit and program will feedback to modulate the infrared light source. The output signal is delivered to an ARM based microprocessor which controls a Power-PMOS and the switch on and off is decided by our proposed Delta-Sigma algorithm. The proposed algorithm gives a ratio value of heating numbers and total sampling numbers which shows a linear relationship with the gas concentration. The experimental results show a good match with our expectation and proposed model, and also it shows a new approach for NDIR gas measurement.
Acknowledgements
This work is supported by National science council in Taiwan (Project MOST 105-2622-E-018-001), and in part by a grant of research help from National Chip Implementation Center (CIC).
Cite this paper
Steven Z. Y. Shen,Chi-Feng Chen,Hilbert C. S. Shen, (2016) A New Pulse Delta-Sigma CO2 NDIR Gas Detector. Optics and Photonics Journal,06,219-225. doi: 10.4236/opj.2016.68B037
References
- 1. Kwon, J., Ahn, G., Kim, G., Kim, J.C. and Kim, H. (2009) A Study on NDIR-based CO2 Sensor to Apply Remote Air Quality Mon-itoring System. Proceedings of 2009 ICCAS-SICE, Fukuoka, 18-21 August 2009, 1683-1687.
- 2. Yi, S.H. Park, Y.W., Han, S.O., Min, N., Kim, E.S. and Ahn, T.W. (2005) Novel NDIR CO2 Sensor for Indoor Air Quality Monitoring. The 13th International Con-ference on Solid-State Sensors, Actuators and Microsystems, Seoul, 5-9 June 2005.
- 3. Shi, J.-J. (2013) A Novel Adaptive Feedback Technique for Non-Dispersive Infrared Gas Concentration Measurement. M.S. Thesis, Department of Mechatronics Engineering, Changhua University, Changhua.
- 4. Leman, O., Mailly, F., Latorre, L. and Nouet, P. (2009) A Wide-Bandwidth, Wide Dy-namic-Range Thermal ΣΔ Architecture for Convective Accelerometers. IEEE Sensors’09 Conference, 25-28 October 2009, Christ-church, 1828- 1831.