Open Access Library Journal
Vol.03 No.09(2016), Article ID:70960,13 pages
10.4236/oalib.1103023
Applications of Image Morphing Techniques to Analyze Changes in Our Environment
Tanvir Prince1, Yanicel Fragoso1, Ousmane Gaye2
1Department of Mathematics, Eugenio María de Hostos Community College, The City University of New York, Bronx, NY, USA
2Department of Natural Science, Eugenio María de Hostos Community College, The City University of New York, Bronx, NY, USA

Copyright © 2016 by authors and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 31, 2016; Accepted: September 25, 2016; Published: September 28, 2016
ABSTRACT
This research is conducted in the summer of 2016 and it is supported by several agencies, such as the CILES grant of Prof. Angulo Nieves, professor of Mathematics at Hostos Community College and the New York City Research Initiative1. The team is part of the summer program CCRI associated to NASA. This research paper is the result of the work done in this program1. The purpose of this research is to analyze the mathematics behind image morphing and its usage towards environmental changes. Image morphing is considered an average between two different images or the gradual transition from one image to another. In other words, we take two time- varying pictures and compare them as if positioned one on top of the other. Assuming one image is at time t = 0 and the other at t = 1, we can predict what would be the point’s location at any time “t” between them, generating its corresponding triangle pattern and therefore its image. The process to morph a pair of images begins with the selection of key points that transform from one image to the next. Triangulation of an image is the distribution of those key points along an image creating small triangles. The morph is applied from triangle to triangle by affine transformations that distort and blend two images [1] . This procedure represents the basics of morphing calculations using linear algebra parameterization of line segments to determine the path and final location of each point compared to the rest. In real life, each image has a large number of points and triangles that form the triangulation pattern, and for this reason we use different application software to create image morphs. Abrosoft Fantamorph Deluxe 5.0 [2] software is used in this research to create a series of time- varying frames. This research studies the slow changes that occur on various environments along the planet. The continuous water decrease in different lakes is analyzed, where the software reveals the transition between two time-varying images. The study of the Global Water Crisis is performed creating frames of the map from 1995 to 2025. In this particular case, we can predict the countries in the world that will be affected at any year of the time frame including the future. In addition, we compare the snowpack in Sierra Nevada, California images taken in March 2010 and March 2015. With the morphs between these two images, we can determine the rate in which the snowpack decreases during the five years. Image morphing provides important findings on the changes in our environment while contributes to research agencies as NASA. The main limitation encountered in this research is that Abrosoft Fantamorph only permits the creation of morphs as linear functions. For further research, different software may be used to create morphs as exponential functions
Subject Areas:
Mathematical Analysis
Keywords:
Image Morphing, Abrosoft Fantamorph, Triangulation, Affine Transformation, NASA, CCRI

1. Introduction
The term morph derives from Greek morphē, which means shape or form. Image morphing is the gradual transformation or transition from one image I1 to another I2. In order to truly understand the process behind image morphing, it is important to study the fundamental elements of an image. Images are formed by thousands of pixels; each one represents the smallest part of any image and has its corresponding value. The value of a pixel ranges between 0 and 255 in an 8-bit gray scale. The most common colors use 8-bit numbers, which mean 8 zeros and ones are used for their virtual representation. There are 256 different combinations of 0’s and 1’s for 8-bit binary digits. Each pixel stores a RGB (red, green, blue) value proportional to the light intensity at a particular location. The value zero represents a black color or absence of light. As the pixel value increases, the darkness on that point decreases. When transferring a picture to any computer, we can see the amount of pixels on its width and height as 1050 × 1280 for example. The value of each color is from 0 to 1 and its combination gives a unique color to each pixel that forms the image. Image morphing can be considered as the movement of the pixels; in this project we only study their linear path from an image I1 to its corresponding point in a similar image I2. The mathematics behind image morphs can be explained using linear algebra procedures such as the line integral function over a path in terms of both the RGB values that belong to each pixel and their corresponding positions along the image. Figure 1 shows the pixels that belong to the indicated section of the image.
A morph is completed between two time-varying images taken in the same location or different images with similar features. The average between the two images must assume the time scale from 0 to 1. Figure 2 is an example of a morph between two images with similar features from President Bush to Obama. The position of the pixels is found at different times “t” with the use of mathematical concepts that are discussed in another section of this project. The slow change in the RGB values and in the position of the pixels is expressed as the time changes. When t = 0.25, the image has more characteristics of t = 0, and as well as the image when t = 1 is similar to t = 0.75. The resultant image at t = 0.5 has half features of both images at t = 0 and t = 1 (refer to Figure 2).
In order to create these morphs, we use computer software that generates all the necessary calculations behind the scenes and provides the morphed images. The mathematics behind this process is directly connected to the way the images are expressed in each morph frame depending on the time studied.
2. Fields of Study
Image morphing is incorporated in many areas of study. For example, image morphing is used by the health industry to analyze changes in cells; in forensic science and FBI to recognize physical features a criminal may have after certain time; in the film industry to create special animations and in environmental science to help analyze changes in the environment. The latter application is the main focus of this project. Image morphing is important because it creates an accurate approximation of different images and animations that may be expensive with other methods. Through image morphing, we are able to view gradual changes that occur in our environment. It allows making projections on what is expected to happen in the future and react to these changes in the present.
In this project image morphing is applied to study the changes on the following en-
Figure 1. Representation of image pixels [2] .

Figure 2.Time frame of image morph [3] .
vironments:
1) Poopó Lake (Bolivia);
2) Sierra Nevada Mountains (California);
3) Aral Sea (Central Asia);
4) Freshwater Depletion (Worldwide);
5) Lake Mead Reservoir (Las Vegas);
6) Shasta Mount (California).
3. Methods
A software known as Abrosoft Fantamorph Deluxe 5.0 is used for the completion of this project [2] . This software provides useful and effective features that generate accurate morphs. Fantamorph uses mathematical approaches―it allows the user to view the morph path, key points and triangulations, which are the most important components studied in this project. We can adjust the number of frames created on a morph depending on the time difference between them. In addition, when selecting the key points on image 1, they are automatically transferred to its approximate corresponding location on image 2 that can be modified if needed. Figure 3 shows the key points selected, where the transformation occurs from one image to the next. The bottom image represents the resultant morph image in respect to approximated times between the two top images. That bottom section is where all the morphs are seen and videos can be
Figure 3. Representation of Abrosoft Fantamorph Software [2] .
created to study the transformations, see Figure 3.
Another important feature that Abrosoft Fantamorph offers is the morph path view. This allows the user to observe the displacement of the key points from the starting image to the final image. In Figure 4 & Figure 5, the key points are red color while their displacements follow a yellow dashed line. The displacement process studied in this project follows a linear function that is directly associated to the mathematics behind image morphing.
Furthermore, the software provides the close observation of the triangulation of an image, which is the distribution of key points along an image. The triangles view is helpful because it allows the user to see any overlap of the points, which avoids the image morph to damage; refer to Figure 6.
4. Procedure to Create an Image Morph
1) In order to create an image morph, first select two images that either contain similar
Figure 4. Morph path view on image 1, starting point [2] .
Figure 5. Morph path view on image 2, final point [2] .
Figure 6. Triangulation of the image [2] .
features or are taken in the same space at different times. Then, select key points that belong to image 1. Key points are the significant sections of the image where the transformation occurs. For example, for Figure 2 the key points are the edges of President Bush face, eyes, mouth, etc. These points are selected in terms of relevance in the image; normally in the edges of the items that form the image. When more points are added, more accurate results are expected.
2) Secondly, the key points are connected with line segments along the entire image generating what is known as image triangulation.
3) Create a group of triangles, where the 4 corners’ points remain fixed when the triangles are formed (Figure 7).
The triangulation of an image must meet the following conditions:
・ The line segments form the sides of a set of triangles;
・ The line segments do not intersect;
・ Each vertex point is the vertex of at least one triangle;
・ The union of the triangles is the rectangle (the entire image);
・ The set of triangles is maximal (i.e., no more vertices can be connected) [1] .
4) Modify the position of the key points on the final image. The points move from the first image to their corresponding location on the second. It is important to maintain the same number of key points on both initial and final images; keep the corner points fixed and ensure that the triangles do not overlap. These guarantees that the rectangular shape of the initial image is preserved and that both triangulations are similar [1] . See Figure 8 as an example of the displacement of the key points.
5. Mathematics behind Image Morphing Techniques
Computer programs use linear algebra concepts in order to develop techniques where images can be manipulated in many forms as filters, color corrections, crop, etc. They also allow the adjustments that image morphing imply. Linear algebra techniques are utilized to generate image morphs. The triangulation is the partition of an image into


Figure 7. Key points and triangulation procedure [2] .
Figure 8. Location of the pixels/key points as functions of x and y [4] .
smaller sections based on the key feature points. A morph is applied from triangle to triangle by affine transformations. The mathematics behind morphing starts with the triangulation of the image and follows the steps below [1] :
Given a begin-picture with picture-density ρ0 and an end-picture with picture-den- sity ρ1,
1) Position n vertex points 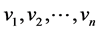 in the begin-picture as key points;
in the begin-picture as key points;
2) Position the corresponding vertex points 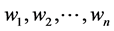 in the end-picture;
in the end-picture;
3) Triangulate both the begin- and end-pictures by drawing line segments that connect the vertex points;
4) For any time t between 0 and 1, find the vertex points 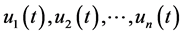 in the morph picture using this formula:
in the morph picture using this formula:
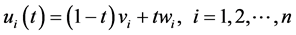
5) Triangulate the morph picture at time t and for each point u find its corresponding vertices ui(t), uJ(t), uK(t) in the triangle that it lies;
6) Express u as convex combination of ui(t), uJ(t) and uK(t) by finding the constants as follows:
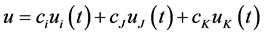 and
and 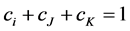
7) Express u and v as convex combinations as well:
 (in the begin picture)
(in the begin picture)
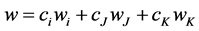 (in the end picture)
(in the end picture)
8) Determine the picture-density ρt(u) of the morph-picture at the point u using:

The equation on step 8 takes weighted average of the RBG levels of the initial and final images to generate the resultant value of the morph image. The weights depend on the fraction of the distances that the vertex points have moved from their beginning positions to their ending positions [1] . The overall RGB levels gradually change when t changes, see Figure 9.
Affine Transformations
Geometric transformations modify the positions of the pixels in the image in order to: create special effects, to register two images taken of the same scene at different times and to morph one image to another [5] . All possible geometric transformations are special cases of the affine mapping or affine transformations.
When A is an orthonormal matrix, it corresponds to a rotation matrix, and the corresponding affine mapping reduces to a geometric mapping [5] . A rotation matrix by this angle is defined as:
Figure 9. Image morph mathematical steps [1] .
Affine transformations allow mapping straight lines to straight lines and between two arbitrary triangles [5] . Affine coefficients can be uniquely determined by the displacement of the three vertices. Each vertex will provide you with six equations, two equations from each of the three vertices. Figure 10 is an example given two triangles, where the pixels are transferred from one to the other with a transformation matrix:
The objective of a morph is to find “an average” between two objects [4] . This average is found between two points P (initial) and Q (final). P and Q could represent the RGB values, points in 3D morphs or an entire image; refer to Figure 11 [1] [4] . Affine combination or linear interpolation is what makes this average possible. For this procedure we follow the formula in the previous section step 1 to calculate the exact position of the average (morph) point. This average point is the green point in Figure 11.
There are two things that we find from this averaging of the points, one is the position and the other is the color RGB value of the point.
For the position of the point:
For the RGB value of the point:
6. Applications of Image Morphing Techniques
6.1. Aral Sea
Image morphing allows us to study the gradual decrease of water in the Aral Sea in the fourteen-year timespan from 2000 to 2014. The lake is located in Central Asia and is the main source of water of the area. We can observe the receding of the coastline, which is most noticeable in the southern part of the lake. This is because Kazakhstan built a dam separating the northern and southern parts of the lake and saved their corresponding side of the lake [6] . From these morphs we can speculate the impact that the drastic
Figure 10. Affine transformation of a triangle [4] .
Figure 11. Averaging of the points [1] [4] .
changes have on humans and wildlife. (Figure 12)
6.2. Sierra Nevada Mountains
The sequence above shows the morph between two images of the Sierra Nevada Mountains in California. The first image was taken on March 31st 2015 and the second image was taken on April 2nd 2016. During this time frame, we are able to observe the gradual increase in snow in a monthly basis. This finding is significant because it represents high snowpack levels after the lowest one was recorded in 2015. Sierra Nevada is also a very important water source. It provides a third of all of the drinking water for the state of California, as well as water to fight wildfires and to generate electricity [8] (Figure 13).
6.3. Freshwater Depletion
The morph above predicts the countries that will be affected by the worldwide problem of freshwater depletion. The first image represents the problem in 1995 while the last image represents the prediction estimated in 2025 (Figure 14). The color blue represents low withdrew of water that increases as it becomes yellow and orange. The images in between, display the progress of this depletion. When observed carefully, we
Figure 12. The Shrinking Aral Sea [6] .
Figure 13. Snowpack in the Sierra Nevada [7] .
Figure 14. Worldwide Issue of freshwater depletion [9] .
can notice that the USA is at risk since the amount of freshwater that is being withdrew is extremely high.
6.4. Lake Mead Reservoir
Las Vegas’ largest reservoir, Lake Mead has declined to its lowest recorded level in history since it was filled in the 1930s [10] . It is speculated that this is because of drastic climate changes that have been occurring. The first image was taken in July 2000 and the last in January 2015. The morph allows a realistic estimation of the changes during the time period. The Lake’s elevation dropped by 120 ft, putting Las Vegas Valley at risk, because it depends on 90% of its water [10] (Figure 15).
6.5. Poopó Lake
In this sequence of morphs we see the devastating changes that occurred to the Poopó Lake, Bolivia’s second largest lake in less than 3 years. The first image was taken in April 2013 and the last one was taken in January 2016. This lake is an important water source for fishing, mining and agriculture [11] . This is the second time the lake dries; the first time was in 1994 due to the same reasons. With the morph of these images we can study how rapidly the lake disappeared and analyze other key features such as causes, consequences in the environment, etc. (Figure 16).
6.6. Shasta Mount
The morphs represent the snowmelt of Shasta Mount from November 2013 to January 2014. It allows us to observe the astonishing rate at which the snow melts in a period of 3 months. The mountain has almost reached its permafrost region [12] . The study of this morph is significant because Shasta Mount represents 37% of the water storage capacity of California [12] (Figure 17).
Figure 15. Lake mead reservoir [10] .
Figure 16. Disappearance of Poopó lake [11] .
Figure 17. Shasta Mount snowmelt [12] .
7. Discussion and Further Research
Image morphing techniques are indeed very useful to analyze changes in our environment. These techniques not only enable us to view changes that are currently occurring, but also changes that happened in the past and predict the ones in the future. Image morphing is not limited to environmental changes analysis since it can be incorporated in other fields. In addition, these techniques are not expensive compared to other methods that are used for the same purposes. Since morphs are based on time-varying images, the result is a sequence of different pictures from the initial picture to the final one. The images that form the sequence depend on a time t at which they are studied in the scale of 0 to 1. The mathematics behind image morphing, which is based on linear algebra techniques, is crucial because it gives accuracy to the resultant morphs from computer software. This mathematics is directly connected to the way the images transform in every frame selected from the morph of two images. It also ensures that the triangles required to create a morph do not overlap with each other. This is important because if the triangles overlap, the resulting morph is pixelated or destroyed. In conclusion, image-morphing techniques contribute to research agencies that may bring possible solutions to the drastic environmental changes that currently affect the world.
For further research, we would recommend better software to improve the accuracy of the results. Although Abrosoft Fantamorph is truly effective, it is limited in certain commands. This software only allows the creation of morphs as linear functions. In the future, other software may be used to study image morphs as exponential functions.
Acknowledgements
・ Dr. Angulo Nieves and Dr. Tanvir Prince
・ Matthew Pearce, National Aeronautics and Space Administration (NASA)
・ NASA Goddard Institute for Space Studies (GISS)
・ NASA Goddard Space Flight Center Office of Education
・ CUNY Hostos Community College
・ CILES Continuous Learning
・ Climate Change Research Initiative (CCRI)
・ Grant from the US Department of Education: #P031C110158
・ United States Department of Education
・ National Science Foundation
Cite this paper
Prince, T., Fragoso, Y. and Gaye, O. (2016) Applica- tions of Image Morphing Techniques to Analyze Changes in Our Environment. Open Access Library Journal, 3: e3023. http://dx.doi.org/10.4236/oalib.1103023
References
- 1. Anton, H. and Rorres, C. (2010) Elementary Linear Algebra: Applications Version. Vol. 10, John Wiley & Sons, Inc., Hoboken.
- 2. (2011) Abrosoft Fantamorph Deluxe 5.0.
http://www.fantamorph.com/index.html - 3. Doyle, M. (2009) Infiniteunknown.net.
http://www.infiniteunknown.net/2009/06/21/obama-now-resembles-bush/ - 4. Efros, A. (2011) Image Warping and Morphing.
- 5. Wang, Y., Guleryuz, O. and Liu, Z. (2011) Geometric Transformations: Warping, Registration, Morphing.
http://eeweb.poly.edu/~yao/EL5123/lecture12_ImageWarping.pdf - 6. Lindsey, R. (2000) Shrinking Aral Sea. 25 August.
http://earthobservatory.nasa.gov/Features/WorldOfChange/aral_sea.php - 7. Hansen, K. (2006) Snowpack in the Sierra Nevada. 26 March.
http://earthobservatory.nasa.gov/Features/WorldOfChange/sierra_nevada.php?all=y - 8. Fleur, N.S.T. (2015) Study Finds Snowpack in California’s Sierra Nevada to Be Lowest in 500 Years. New York Times: A13.
- 9. EverythingConnects Org. (2013) Effects of Human Overpopulation. 13 November.
http://www.everythingconnects.org/overpopulation-effects.html - 10. James, I. (2016) The Desert Sun. 20 May.
http://www.desertsun.com/story/news/environment/2016/05/19/lake-mead-declines-new-record-low/84597120/ - 11. (2016) NASA Earth Observatory Bolivia’s Lake Poopó Disappears.
http://earthobservatory.nasa.gov/NaturalHazards/view.php?id=87363 - 12. (2014) NASA Earth Observatory. The Naked Mountain.
http://earthobservatory.nasa.gov/IOTD/view.php?id=82859
NOTES
1For a complete list of the supporting agencies, please follow the acknowledgement section.




















