Journal of Biomedical Science and Engineering
Vol.09 No.10(2016), Article ID:70768,6 pages
10.4236/jbise.2016.910B018
Comparison of Image Reconstruction Algorithms in EIT Imaging
Benjamin Schullcke1,2, Sabine Krueger-Ziolek1,2, Bo Gong1,2, Ullrich Mueller-Lisse2, Knut Moeller1
1Institute of Technical Medicine, Furtwangen University, VS-Schwenningen, Germany
2Department of Radiology, University of Munich, Munich, Germany




Received: August 30, 2016; Accepted: September 20, 2016; Published: September 23, 2016
ABSTRACT
Electrical Impedance Tomography (EIT) is a medical imaging technique which can be used to monitor the regional ventilation in patients utilizing voltage measurements made at the thorax. Several reconstruction algorithms have been developed during the last few years. In this manuscript we compare a well-established algorithm and a recently developed method for image reconstruction regarding EIT indices derived from the differently reconstructed images.
Keywords:
Electrical Impedance Tomography, Ventilation Monitoring, Image Reconstruction

1. Introduction
Electrical Impedance Tomography (EIT) is a novel medical imaging technique which can be applied to visualize changes of impedance within in the body. Small alternating currents are injected into the body and resulting voltages are measured on the skin surface. In a clinical context EIT is used to trace changes in impedance of the lungs, caused by ventilation [1]. During inspiration the alveoli expand, which lengthens the current pathways and thus increases the impedance of the lungs [2].
Compared to well-established imaging technologies, such as X-ray computed tomography (CT) or magnetic resonance imaging (MRI), EIT has several advantages. No radiation is needed for image acquisition, which makes EIT suitable for frequent examinations or long term monitoring. Additionally, the necessary technical equipment is portable and inexpensive, which enables ventilation monitoring at the bedside.
Usually, in commercially available EIT-systems for lung imaging, an array of 16 to 32 electrodes is attached around the circumference of the chest. A pair of electrodes is used for current injection and the resulting voltage between the remaining electrodes is measured. Subsequently, the pair of electrodes used for current injection is changed in a rotating manner. The measured voltages are used to reconstruct images of conductivity change. The voltage measurements can be done relatively fast and enables frame rates in commercially available system of up to 50 frames/second. Thus EIT is capable of to monitoring rapid processes in the lungs, which are currently not detectable with CT or MRI.
However, a drawback of EIT is that the reconstructed image of conductivity change does not depict a thorax slice of well defined thickness, as e.g. in CT imaging. The diffuse current propagation in the thorax results in a lens-shaped volume, whose impedance changes are projected onto a two-dimensional image. As a result, impedance changes above or below the electrode plane are also reflected in the reconstructed image.
The challenge in EIT imaging is to reconstruct changes of conductivity inside a domain based on voltage measurements on the boundary of the domain. This problem is ill-posed, meaning that arbitrarily small changes in measured voltages may result in arbitrarily large values of reconstructed conductivity. The ill-posedness is usually addressed with regularization, forcing the solution, i.e. the reconstructed change in conductivity, to be either small, smooth or slowly changing.
Recently, we have developed an approach for image reconstruction including patient specific structural information (obtained e.g. from CT or MRI data) into the reconstruction process [3]. This approach facilitates the superposition of reconstructed images of conductivity change and structural images and thus provides a broader insight into the pathophysiology of the lungs.
In this paper we compare two different approaches for images reconstruction. Two EIT derived parameters, the “Center of Ventilation” (CoV) and the “ventilation shift” (vShift) are evaluated.
2. Methods and Material
2.1. Simulation Model
Calculations in this work have been carried out using Matlab 2015a (Mathworks, Natick, USA) and the EIDORS toolbox [4]. Finite element models (FEM) were generated using NETGEN [5].
In this paper the “adjacent current stimulation pattern” was used, where currents are injected and voltages are measured between neighboring electrodes. For the considered 16 electrode system this results in 208 voltages for every frame, of which 104 are independent.
Boundary voltages for end-expiration and end-inspiration were simulated on a 3D FEM model, generated from a CT dataset. The contour of the thorax at the 5th intercostal space was used for the outline of the model. FEM elements not-corresponding to lung tissue were assigned to a conductivity of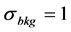 . Voltages at end-expiration
. Voltages at end-expiration 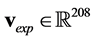 were simulated with FEM elements corresponding to lung tissue set to a conductivity of
were simulated with FEM elements corresponding to lung tissue set to a conductivity of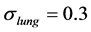 . Voltages at end-inspiration
. Voltages at end-inspiration 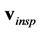 were simulated for varying values of conductivity in the lungs:
were simulated for varying values of conductivity in the lungs:
a) Conductivity of right lung systematically varying between 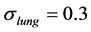 and
and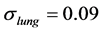 , with conductivity of right lung set to
, with conductivity of right lung set to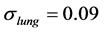 .
.
b) Conductivity of dorsal lung systematically varying between 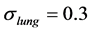 and
and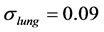 , with conductivity of ventral lung set to
, with conductivity of ventral lung set to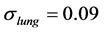 .
.
In this manuscript we use unit-less values for conductivity. The values for conductivity are based on the values published by Witsoe and Kinnen, whereas a collapsed lung has a conductivity of 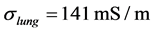 and a conductivity of
and a conductivity of 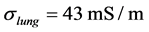 at maximum inflation [6]. FEM elements not belonging to the lungs correspond to a conductivity of
at maximum inflation [6]. FEM elements not belonging to the lungs correspond to a conductivity of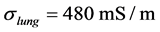 , according to the values in [7].
, according to the values in [7].
Figure 1(a) shows the FEM model used for simulation of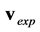 . Two exemplary models for the simulation of
. Two exemplary models for the simulation of 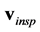 are depicted in Figure 1(b) and Figure 1(c), with lower ventilation in the right lung and the dorsal parts of both lungs, respectively.
are depicted in Figure 1(b) and Figure 1(c), with lower ventilation in the right lung and the dorsal parts of both lungs, respectively.
2.2. Image Reconstruction
The EIT problem is usually formulated as shown in Equation (1)
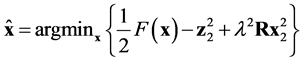 (1)
(1)
with z being the relative change in voltage, where 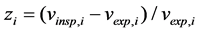 and i denotes the i-th element of the vectors
and i denotes the i-th element of the vectors 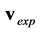 and
and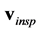
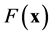
Figure 1. FEM models used for simulation of boundary voltages.
where R forces the solution 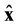
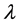
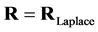
In linearized EIT imaging the forward model is linearized around a conductivity distribution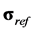
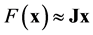
and each element 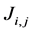
Thus, for linearized EIT Equation (1) can be solved in a closed form:
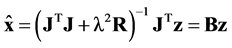
The solution of the EIT problem according to Equation (3) can be regarded as classical approach with one-step Gauss-Newton solver (one-step GN).
This reconstruction method is compared with the above mentioned approach, where patient specific morphological prior information is used in the reconstruction process. In this case the Jacobian J is replaced with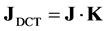
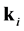
2.3. EIT Parameters
Images were reconstructed with the one-step GN solver and with the DCT approach. For both approaches the “ventilation shift” (vShift) and the “Center of Ventilation” (CoV) are calculated, where
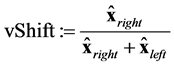
with 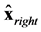
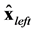
The “Center of Ventilation” (CoV) is defined as:

with 
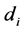
3. Results
Exemplary reconstructions with the GN solver and the DCT approach are depicted in Figure 2 for lower ventilation in the left lung.
Figure 3 shows vShift values and CoV values for both reconstruction methods. Although the reconstructed images are different, the derived vShift and CoV values show only slight differences, which is revealed in Figure 3.
4. Discussion
Several EIT reconstruction methods have been developed during the past years. It has already been demonstrated that indices for EIT image analysis, such as “CoV” or “vShift” are not influenced from the reconstruction method [9]. In this simulation
Figure 2. Left: Reconstruction of conductivity change with DCT approach. Right: Reconstruction with standard GN solver using Laplace prior.
Figure 3. Top: vShift value for different reconstruction methods. Bottom: CoV value.
study we used an algorithm including patient specific morphological information in the reconstruction process in comparison with a standard approach. Results demonstrate that both EIT indices show only slight differences for the different reconstruction methods. Reconstruction methods including morphological information might be used if the structural information is available. In patients where an actual CT or MRI dataset is not available standard EIT reconstruction algorithms, as the used one-step GN with Laplace prior still gives valuable information regarding the examined EIT indices.
Acknowledgements
This work is partially supported by the Federal Ministry of Education and Research (BMBF) under grant no. 03FH038I3 (MOSES).
Cite this paper
Schullcke, B., Krueger-Ziolek, S., Gong, B., Mueller-Lisse, U. and Moelle, K. (2016) Comparison of Image Reconstruction Algorithms in EIT Imaging. J. Biomedical Science and Engineering, 9, 137-142. http://dx.doi.org/10.4236/jbise.2016.910B018
References
- 1. Gong, B., Krueger-Ziolek, S., Moeller, K., Schullcke, B. and Zhao, Z. (2015) Electrical Impedance Tomography: Functional Lung Imaging on Its Way to Clinical Practice? Expert Review of Respiratory Medicine, 9, 721-737. http://dx.doi.org/10.1586/17476348.2015.1103650
- 2. Leonhardt, S. and Lachmann, B. (2012) Electrical Impedance Tomography: the Holy Grail of Ventilation and Perfusion Monitoring? Intensive Care Med, 38, 1917-1929. http://dx.doi.org/10.1007/s00134-012-2684-z
- 3. Schullcke, B., Gong, B., Krueger-Ziolek, S., Soleimani, M., Mueller-Lisse, U. and Moeller, K. (2016) Structural-Functional Lung Imaging Using a Combined CT-EIT and a Discrete Cosine Transformation Reconstruction Method. Scientific Reports, 6, 25951. http://dx.doi.org/10.1038/srep25951
- 4. Adler, A. and Lionheart, W.R. (2006) Uses and Abuses of EIDORS: An Extensible Software Base for EIT. Physiol Meas, 27, S25-S42. http://dx.doi.org/10.1088/0967-3334/27/5/s03
- 5. Schöberl, J. (1997) NETGEN An Advancing Front 2D/3D-Mesh Generator Based on Abstract Rules. Computing and Visualization in Science, 1, 41-52. http://dx.doi.org/10.1007/s007910050004
- 6. Witsoe, D. and Kinnen, E. (1967) Electrical Resistivity of Lung at 100 kHz. Medical and Biological Engineering, 5, 239-248. http://dx.doi.org/10.1007/BF02474533
- 7. Adler, A., Amato, M.B., Arnold, J.H., Bayford, R., Bo-denstein, M., Bohm, S.H., et al. (2012) Whither Lung EIT: Where Are We, Where Do We Want to Go and What Do We Need to Get There? Physiol Meas, 33, 679-694. http://dx.doi.org/10.1088/0967-3334/33/5/679
- 8. Frerichs, I., Dargaville, P.A., van Genderingen, H., Morel, D.R. and Rimensberger, P.C. (2006) Lung Volume Recruitment after Surfactant Administration Modifies Spatial Distribution of Ventilation. American Journal of Respiratory and Critical Care Medicine, 174, 772-779. http://dx.doi.org/10.1164/rccm.200512-1942OC
- 9. Zhao, Z., Frerichs, I., Pulletz, S., Muller-Lisse, U. and Moller, K. (2014) The Influence of Image Reconstruction Algorithms on Linear Thorax EIT Image Analysis of Ventilation. Physiol Meas, 35, 1083-1093. http://dx.doi.org/10.1088/0967-3334/35/6/1083




