ABSTRACT

Single nucleotide polymorphisms (SNPs), which are the most common form of DNA variations, have great potential as a medical diagnostic tool. However, compared to the number of SNPs involved, the available training data sets generally have a fairly small sample size, which is a main challenge to traditional data analysis methods. This paper proposed an improved univariate marginal distribution algorithm (UMDA) named multi-population UMDA (MPUMDA) for disease association study. In order to illustrate the effectiveness of our algorithm, we compared it with some current known methods, and the results showed that our method is potentially interesting as an alternative tool in disease association study.

Keywords:

Single Nucleotide Polymorphisms, Disease Association Study, Feature Selection

1. Introduction

The risk of common diseases is likely determined by complex interplay between several genetics [1]. Common genetic variations, i.e. the single nucleotide polymorphisms (SNPs), are believed to modulate diseases susceptibility [2]. Therefore, the main task of human genetics is to understand the mapping relationship between SNPs and susceptibility of disease [3]. Knowing that an individual is (or is not) susceptible to (or belong to risk group for) a certain disease will help us greatly reduce the cost of preventive measures or even completely avoid disease development.

Although most of SNPs are neutral, certain of them are functional and affect the phenotype, such as skin color and different resistances to infection or drug responses [4]. The improvement of high-throughput SNPs genotyping methods generates huge quantities of SNPs data. However, only a small number of SNPs show strong correlation with a certain disease compared to the total number of SNPs investigated [5]. Thus feature selection is crucial for this study. Estimation of distribution algorithms (EDAs) are one of the population-based stochastic algorithms. In this paper, we propose an improved univariate marginal distribution algorithm (UMDA) named multi-popula- tion UMDA (MPUMDA) for diseases association study. The proposed algorithm was tested on three disease datasets: Crohn’s disease, Lung cancer and Tick-borne encephalitis [6]. The results were compared with those obtained by some other algorithms. Experimental results showed that the proposed method can improve classification accuracy remarkably.

2. Background

2.1. Single Nucleotide Polymorphism

One single nucleotide of A, C, G or T in the DNA sequence is replace by any other 3 nucleotides, e.g., from CCCTAC to CCTTAC, we call this variation (C à T) as single nucleotide polymorphism (SNP). It has the following three characteristics: 1) very common in the human genome (it is estimated that the number of SNPs in the human genome is about 12 million); 2) among the SNPs, two out of every three SNPs are the variation from cytosine (C) to thymine (T); 3) very stable from generation to generation.

2.2. Diseases Association Study

Disease association study is to identify factors that may contribute to a medical condition by comparing the cases (subjects who have that condition) with controls (subjects who do not have the condition).

Assume that we have m samples (each sample has n SNPs/features and the disease status).

Let 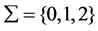denote the value of each SNP, where 0 and 1 stand for homozygous sites with major and minor allele, respectively, and 2 stands for heterozygous sites.

We use to represent an individual sample, where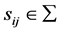, 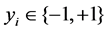(−1 stands for case and +1 stands for control), ,.

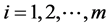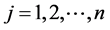Let 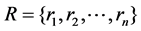represent the feature set, where correspond to the n SNPs.

The goal of this study is to select a least redundant feature subset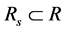 with predicting power for disease status. Then the problem can be described as the following model.

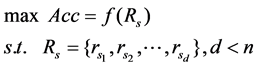(1)

3. Methods

3.1. Univariate Marginal Distribution Algorithm (UMDA)

EDAs have been proposed for the purpose of overcoming some drawbacks that classical EAs presented. The advantage of EDAs over classical EAs is the reduction in the number of parameters to be tuned. Univariate Marginal Distribution Algorithm (UMDA) presented for the first time by Mühlenbein is one of the simplest algorithms in the EDAs family [7]. The UMDA sorts M individuals by their fitness value from high to low, and then selects N best ones to estimate the probability distribution 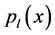at each generation. The probability distribution for the l-th iteration is defined as follow. The pseudocode of UMDA is presented in Figure 1.

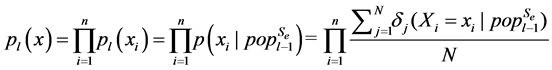(2)

where n is the number of variables, and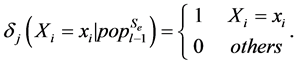

3.2. Multi-Population UMDA

In UMDA, lack of diversity, particularly during the latter stages of the optimization, is the dominant factor for converging to local optimum solutions. To improve the capability of UMDA, multi-population UMDA (MPUMDA) is proposed in this paper. MPUMDA is an extension of traditional UMDA by dividing the population into three sub-groups (best, middle and worst) according to their performances. Each sub-group executes UMDA separately. At the end of each generation, sub-groups are reassigned to ensure information sharing.

3.3. MPUMDA for Feature Selection and Parameters Optimization

The largest problems encountered in setting up the SVM model are how to select the kernel function and its parameters [8]. However, optimizing feature subsets and SVM model parameters respectively may not be reached the good results. Therefore, we use the MPUMDA to optimize the SVM model parameters and feature subsets simultaneously.

1) Individual representation

An individual of MPUMDA comprises two parts: the features mask and the SVM model parameters. The part of SVM model parameters consists of two sub-parts: kernel function type and other parameters. Figure 2 shows the representation of an individual with N dimensions.

In Figure 2, represent features mask. 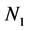is the number of SNPs. For the feature mask, the bit with value ‘1’ indicates the SNP is selected and “0” indicates not.

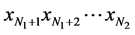represent kernel function types.

And represent the related kernel parameter and the penalty parameter C.

2) Fitness definition

Classification accuracy is often used as a criterion to design fitness function. However, due to the difficulty in obtaining clinical information on patients, the data used in disease association studies are often imbalanced. The traditional accuracy measure may be misleading since the all-negative classifier may achieve a good measure value. Thus, the is used as the fitness function which is able to deal with imbalanced dataset.

4. Experiments and Results

In this section, MPUMDA-SVM is test on three datasets: Crohn’s disease, Lung cancer and Tick-borne encephalitis [6] and the results are compared with several current known algorithms. The 5-fold method was used in this paper.

4.1. Datasets

In this subsection, we focus on the selection of the best combination of SNPs with maximal difference between case and control groups. Three datasets used in this study are summarized in Table 1.

4.2. Results

Firstly, in order to verify the effectiveness of MPUMDA-SVM, we compared it with sequential forward search (SFS), UMDA with SVM and the method proposed in [8] (Table 2). The numbers of individuals and iterations were set to 60 and 100, respectively. It is clearly that, the accuracy of SVM with feature selection outperformed that without feature selection. This means that not all features are necessary to achieve total classification accuracy. The classification accuracy on Crohn’s disease data set obtained by MPUMDA-SVM was 93.3%, whereas, only 81.4%, 84.8% and 89.6% was obtained by SFS, UMDA or PSO with SVM, respectively. For the Lung cancer and Tick-borne

encephalitis datasets, the classification accuracy obtained by our method (87.9% and 96.4%) was also better than that of other algorithms. Therefore, we may draw the conclusion that the MPUMDA is able to select more relevant SNPs.

Figure 3 shows that the number of SNPs can be reduced by MPUMDA-SVM. The percentage of SNPs selected was reduced to 0.068 and 0.171 for the Crohn’s disease and Tick-borne encephalitis datasets, respectively. However, for the Lung cancer dataset, the percentage of SNPs selected was only reduced to 0.588. That can be explained by the fact that Lung cancer is a more complex disease than the other two.

Finally, we did some further analysis using the selected SNPs. Figure 4 and Figure 5 shows the frequencies of 0, 1 and 2 in the selected SNPs for above three data sets. From Figure 4 we can see that at 57, 86 and 95 the frequency of 2 in the controls group is higher than that in cases group. 1’s frequency is almost equal to zero at 9 and 85 in case and control group respectively. Those 7 SNPs combination is mostly association with Crohn’s disease. We can see from the Figure 5 that almost in all the sites 0’s frequencies are higher in case group than controls. In addition, 1’s frequency is zero in SNP 1, which can be regarded as a risk factor of tick-borne encephalitis.

5. Conclusion

Due to the high genotyping cost in association studies, it is desirable to find a least redundant subset of SNPs with the highest prediction accuracy for complex diseases. In this paper, a multi-population univariate marginal distribution algorithm (MPUMDA) is used to implement the feature selection, and support vector machine (SVM) serves as an evaluator of MPUMDA for disease association study. The merit of our proposed approach is that MPUMDA is capable of finding the optimal feature subset and SVM model parameters simultaneously. Experimental results show that the proposed approach achieves the highest classification accuracy for all the datasets when compared with some current known methods, that is, it is potentially interesting as an alternative tool in disease association study.

Acknowledgements

The research is supported by Foundation of Engineering College of APF (WJY201518) and (JLX201648). Thanks to Dr. Dumitru Brinza for providing the dataset.

Cite this paper

Wei, B. (2016) A Hybrid Algorithm for Disease Association Study. J. Biomedical Science and Engineering, 9, 129-136. http://dx.doi.org/10.4236/jbise.2016.910B017

References