World Journal of Engineering and Technology
Vol.04 No.03(2016), Article ID:70719,7 pages
10.4236/wjet.2016.43C009
Analysis on Fracture Mechanics of Unstable Rock
Siqi Chen, Hongkai Chen, Ming Yang, Tao Chen, Kexuan Guo
College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang, China




Received: April 28, 2016; Accepted: August 20, 2016; Published: September 22, 2016
ABSTRACT
Unstable rock is a kind of global geological disaster with high frequency. This paper, considering three kinds of combined loads which are gravity, fracture water pressure and seismic force, constructs a unstable rock mechanics model and it uses a fracture mechanics method to deduce the composite stress intensity factor of the type I - II. Based on the maximum circumferential stress theory, this article calculates the theoretical fracture angle by triangle universal formula.
Keywords:
Fracture Mechanics, Composite Stress Intensity Factor, Fracture Angle, Unstable Rock

1. Introduction
Rock is a complex structure which is naturally produced by one or more minerals under geological conditions. In the rock engineer, most rocks belong to pressure-shear condition. Therefore, it is necessary and urgent for the study of unstable rock in pressure-shear condition. A lot of scholars have devoted themselves to the study of unstable rock. For example, Nara Y. etc. [1] had found that fissure water would accelerate the speed of the subcritical crack growth of granite and affect the structural strength of the granite; With rock surrounding the Skolis Mountain and the Acrocorinthos area as the research object, Zygouri V. etc. [2] showed that shallow earthquakes could cause a wide range of rock collapse; Chen H. K. etc. [3] put forward the failure criterion of unstable rock under the excitation effect and established the evaluation method for its safe; Johari A. etc. [4] used the method of joint distribution of random variables to evaluate the stability of rock in the critical state; Li Y. etc. [5] simulated the crack development of rock mass under the action of water pressure by using FLAC3D software, and the studies showed that the strength and stability of the jointed rock mass was obviously decreased; Liang L. etc. [6] sampled the shale in the Long maxi area, and the research results showed that the aqueous liquid of had significant positive impact in Crack growth of shale. However, So far, many scholars have studied the rock crack by the method of experiment and numerical analysis, and the theoretical analysis of the rock crack is slightly deficient. This text used the method of fracture mechanics to deduce the unstable rock, and the results have certain theoretical guiding significance and economic value for prevention of disaster and engineering safety assessment.
2. Coordinate Transformation of Stress Components
Figure 1 is a rock model of establishment. Where is center of gravity of unstable rock; u is Fissure water pressure of control fissure; PL is horizontal seismic force per unit length; PV is vertical seismic force per unit length; W is Gravity of rock mass per unit length.
In Figure 1, the crack tip selects a unit. The pressure-shear stress is formed under the gravity of the rock itself. As shown in Figure 2.
In the straight line of the unit which parallel to the 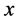 axis, the included angle between the outer normal and the coordinate axes is
axis, the included angle between the outer normal and the coordinate axes is 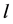 and
and 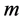 respectively. We may know
respectively. We may know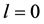 ,
, 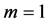 ,
, 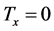 and
and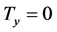 . The known parameters are brought into the boundary condition equation
. The known parameters are brought into the boundary condition equation
Figure 1. The unstable rock model.
Figure 2. Crack stress at the tip of the element.
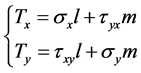 (1)
(1)
It will find 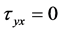 and
and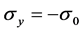 . In the straight line of the unit which parallel to the
. In the straight line of the unit which parallel to the 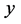 axis, it can know
axis, it can know 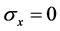 and
and 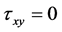 in the same way. As we all know:
in the same way. As we all know:
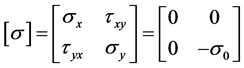 . (2)
. (2)
A new and old coordinate system is established in Figure 3. Where 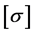 is Stress tensor of the old coordinate system;
is Stress tensor of the old coordinate system; 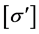 is Stress tensor of the new coordinate system. The projection of
is Stress tensor of the new coordinate system. The projection of 





It can know



Combining formula (2), formula (3), formula (4) and formula (5) can be obtained

By formula (6) can be known

3. Deduction of Type I and Type II Stress Intensity Factor
The article assumes 

Figure 3. The old and new coordinate system.

Because of 




We can carry out partial differential to Westergaard stress function



From formula (13), formula (14) and formula (15), we can get

As shown in Figure 4, there is a center crack with a length of 









The stress function is obtained

The original O point translates to the new coordinate O' point. We assume complex coordinates of any new coordinates of a bit is

Combining formula (16) and formula (17)

Figure 4. Type I crack under bidirectional uniform stress.
When

Because of

Combining formula (18), formula (19) and formula (20), we can obtain

We can use the same way to get

4. Composite Stress Intensity Factor and Fracture Angle for Unstable Rock
At first, we suppose that composite stress intensity factor is

Because the horizontal seismic force (PL) and vertical seismic force (PV) can not be considered at the same time. So we can add a coefficient C1 and C2 in front of them respectively. It builds the following functions

where the coordinates of the center of gravity of the unstable rock is






If D1 and D2 are constants, according to Westergaard’s stress function, we will get

Combining formula (7), formula (21), formula (22), formula (23), formula (27), we will calculate

According to the maximum circumferential stress theory [8], we will get fracture angle

We put trigonometric function into formula (29), and it will get

When it is negative (“−”), fracture angle is greater than 180˚. Obviously, it is not in conformity with the actual situation. So fracture angle is

5. Conclusion
Considering gravity, fracture water pressure and seismic force, this paper constructs unstable rock mechanics model, which is very common in the rock engineer. What’s more, we derive composite stress intensity factor of the type I - II by fracture mechanics. And according to the maximum circumferential stress, we calculate theory Fracture angle by trigonometric function. In short, the results have certain theoretical guiding significance and economic value for prevention of disaster and engineering safety assessment.
Cite this paper
Chen, S.Q., Chen, H.K., Yang, M., Chen, T. and Guo, K.X. (2016) Analysis on Fracture Mechanics of Un- stable Rock. World Journal of Engineer- ing and Technology, 4, 69-75. http://dx.doi.org/10.4236/wjet.2016.43C009
References
- 1. Nara, Y., Oe, Y., Murata, S., et al. (2015) Estimation of Long-Term Strength of Rock Based on Subcritical Crack Growth. Engineering Ge-ology for Society and Territory, Volume 2. Springer International Publishing, 2157-2160.
- 2. Zygouri, V. and Koukouvelas, I.K. (2015) Evolution of Rock Falls in the Northern Part of the Peloponnese, Greece. IOP Conference Series: Earth and Environmental Science, IOP Pub-lishing, 26, Article ID: 012043.
- 3. Chen, H.K., Zhou, Y.T. and Wang, Z. (2014) Study on Damage Characteristics of Unstable Rocks under Excitation Effect. Applied Mechanics and Materials, 459, 575-581. http://dx.doi.org/10.4028/www.scientific.net/AMM.459.575
- 4. Johari, A., Momeni, M. and Javadi, A.A. (2015) An Analytical Solution for Reliability Assessment of Pseudo-Static Stability of Rock Slopes Using Jointly Distributed Random Variables Method. Iranian Journal of Science and Technology Transactions of Civil Engineering, 39, 351-363.
- 5. Li, Y., Zhou, H., Zhu, W., et al. (2015) Numerical Study on Crack Propagation in Brittle Jointed Rock Mass Influenced by Fracture Water Pressure. Materials, 8, 3364-3376. http://dx.doi.org/10.3390/ma8063364
- 6. Liang, L., Xiong, J. and Liu, X. (2015) Experimental Study on Crack Propagation in Shale For-mations Considering Hydration and Wettability. Journal of Natural Gas Science and Engineering, 23, 492-499. http://dx.doi.org/10.1016/j.jngse.2015.02.032
- 7. Westergaard, H.M.W. (1939) Bearing Pressures and Cracks. Journal of Applied Mechan-ics, 6, A49-A53.
- 8. Erdogan, F. and Sih, G.C. (1963) On the Crack Extension in Plates under Plane Loading and Transverse Shear. Journal of Basic Engineering, 85, 519-525. http://dx.doi.org/10.1115/1.3656897





