Open Access Library Journal
Vol.03 No.09(2016), Article ID:70582,8 pages
10.4236/oalib.1102895
On Starlike Functions Using the Generalized Salagean Differential Operator
Saliu Afis1, Mashood Sidiq2
1Department of Mathematics, Gombe State University, Gombe, Nigeria
2Department of Mathematics, University of Ilorin, Ilorin, Nigeria
Copyright © 2016 by authors and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 19, 2016; Accepted: September 11, 2016; Published: September 14, 2016
ABSTRACT
In this paper we investigate the new subclass of starlike functions in the unit disk  via the generalized salagean differential operator. Basic properties of this new subclass are also discussed.
via the generalized salagean differential operator. Basic properties of this new subclass are also discussed.
Subject Areas:
Mathematical Analysis
Keywords:
Salagean Differential Operator, Starlike Functions, Unit Disk, Univalent Functions, Analytic Functions and Subordination

1. Introduction
Let 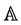 denote the class of functions:
denote the class of functions:
 (1)
(1)
which are analytic in the unit disk . Denote by
. Denote by 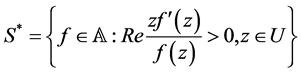 the class of normalized univalent functions in U.
the class of normalized univalent functions in U.
Let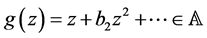 . We say that
. We say that 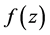 is subordinate to
is subordinate to 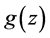 (written as
(written as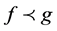 ) if there is a function w analytic in U, with
) if there is a function w analytic in U, with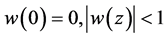 , for all
, for all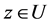 . If g is univalent, then
. If g is univalent, then 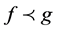 if and only if
if and only if 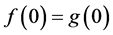 and
and 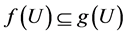 [1] .
[1] .
Definition 1 ( [2] ). Let 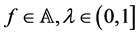 and
and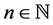 . The operator
. The operator 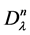 is defined by
is defined by
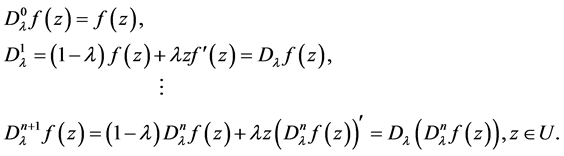 (2)
(2)
Remark 1. If 


Remark 2. For 
From (2), the following relations holds:

and from which, we get

Definition 2 ( [3] ). Let

with
This operator is a particular case of the operator defined in [3] and it is easy to see that for any

Next, we define the new subclasses of
Definition 3. A function 


Remark 3.
Remark 4. 

Definition 4. Let



i) 


ii) 

iii) 



Several examples of members of the set 
2. Preliminary Lemmas
Let P denote the class of functions 

Lemma 1 ( [5] [7] ) Let 




i)
ii) 


More general concepts were discussed in [4] - [6] .
Lemma 2 ( [8] ). Let 






If the differential subordination:

has univalent solution 


The formal solution of (6) is given as

where
and
see [9] [10] .
Lemma 3 ( [9] ). Let 







3 Main Results
Theorem 1. Let 







Proof. From (4), we have
If we suppose



Now, let
Then
By (2) and (3) we have

Applying Lemma 2 with 

Theorem 2. Let 





where
is the best dominant.
Proof. Let
By (9), we have
where
To show that
Now, considering the differential equation
whose solution is obtained from (8). If we proof that 
sult follows trivially from Lemma 2. Setting 

i)
ii)
where
Therefore, 
iii)
so that
Hence, 
Theorem 3.
Proof. Let
From (9), let 








Corollary 1. All functions in 
Proof. The proof follows directly from Theorem 3 and Remark 4.W
Corollary 2. The class 
Proof. The proof is obvious from the above corollary and Definition 4.W
The functions 


Theorem 4. The class 

Proof. let


Applying 

Let 

Let 





Theorem 5. Let
for some
Proof. Let

But
Applying the operator in Definition 2, we have the result.W
With

Theorem 6. Let
The function 
Proof. Let



Theorem 7. Let
and
where
Proof. Let
and
for
Also, upon differentiating
and
for
Acknowledgements
The authors appreciates the immense role of Dr. K.O. Babalola (a senior lecturer at University of Ilorin, Ilorin, Nigeria) in their academic development.
Cite this paper
Afis, S. and Sidiq, M. (2016) On Starlike Functions Using the Generalized Salagean Differential Operator. Open Access Library Journal, 3: e2895. http://dx.doi.org/10.4236/oalib.1102895
References
- 1. Duren, P.L. (1983) Univalent Functions. Springer Verlag, New York Inc.
- 2. Al-Oboudi, F.M. (2004) On Univalent Functions Defined by a Generalized Salagean Operator. International Journal of Mathematics and Mathematical Sciences, 27, 1429-1436.
http://dx.doi.org/10.1155/S0161171204108090 - 3. Faisal, I. and Darus, M. (2011) Application of a New Family of Functions on the Space of Analytic Functions. Revista Notas de Matemtica, 7, 144-151.
- 4. Babalola, K.O. and Opoola, T.O. (2006) Iterated Integral Transforms of Caratheodory Functions and Their Applications to Analytic and Univalent Functions. Tamkang Journal of Mathematics, 37, 355-366.
- 5. Miller, S.S. and Mocanu, P.T. (1978) Second Order Differential Inequalities in the Complex Plane. Journal of Mathematical Analysis and Applications, 65, 289-305.
http://dx.doi.org/10.1016/0022-247X(78)90181-6 - 6. Miller, S.S. and Mocanu, P.T. (2000) Differential Subordination, Theory and Applications. Marcel Dekker, 2000.
- 7. Babalola, K.O. and Opoola, T.O. (2008) On the Coefficients of Certain Analytic and Univalent Functions. In: Dragomir, S.S. and Sofo, A., Eds., Advances in Inequalities for Series, Nova Science Publishers, 5-17.
http://www.novapublishers.com - 8. Eenigenburg, P., Miller, S.S., Mocanu, P.T. and Read, M.O. (1984) On Briot-Bouquet Differential Surbordination. Revue Roumaine de Mathématiques pures et Appliquées, 29, 567-573.
- 9. Miller, S.S. and Mocanu, P.T. (1983) Univalent Solution of Briot-Bouquet Differential Equations. Lecture Notes in Mathematics, 1013, Springer Berlin/Heidelberg, 292-310.
- 10. Srivastava, H.M. and Lashin A.Y. (1936) Some Applications of the Briot-Bouquet Differential Surbordination. Journal of Inequalities in Pure and Applied Mathematics, 37, 374-408.



































