ABSTRACT

The vapor pressure (VP) of 87 grade gasoline was measured using an enhanced VP acquisition system over a temperature range of approximately 19.0˚C (292.2 K) and 69.0˚C (342.2 K). The empirical data were used to predict the thermodynamic entities the enthalpy of vaporization (ΔH_vap) and the entropy of vaporization (ΔS_vap) of gasoline. The results of this investigation yielded a ΔH_vap value of 35.1 kJ/mol and ΔS_vap of 102.5 J/mol∙K. The value of ΔH_vap was in excellent agreement with the findings of a prior study (Balabin et al., 2007), which produced a ΔH_vap values of 37.3 kJ/mol and 35.4 kJ/mol. The enthalpy and entropy of vaporization of n-heptane (37.2 kJ/mol and 100.1 J/mol∙K) and n-octane (39.1 kJ/mol and 98.3 J/mol∙K) were also determined after acquiring VP data for the two VOCs. The empirical results for n-heptane and n-octane were also in excellent agreement with the literature. These favorable comparisons strengthen the capacity of our system for acquiring the VP data for pure and volatile multi-component mixtures.

Subject Areas:

Physical Chemistry

Keywords:

Gasoline, Vapor Pressure (VP), Enthalpy of Vaporization, Entropy of Vaporization, Volatile Organic Compounds (VOCs)

1. Introduction

Automotive gasoline is a major product manufactured by the petroleum industry. The vapor pressure (VP) is a key physical property of automotive gasoline as well as aviation fuels. Gasoline is a petroleum fuel that is highly volatile. It is refined product of crude oil consisting of a mixture of hydrocarbons, additives, and blending agents. The VP is critically important for both automotive and aviation gasoline; this is due to these fuels being manufactured as liquids, but consumed in the vapor phase. Thus, high volatility is a prerequisite for a gasoline to ensure sufficient engine start-up, warm-up and acceleration under routine driving and flying conditions [1] [2] . The VP of gasoline is also vital for predicting the concentration of volatile compounds discharged into the atmosphere via the combustion of the fuel.

There are a number of methods for determining the VP and they are somewhat time- consuming. The Reid vapor pressure (RVP) is typically the measurement of choice for ascertaining the volatility of commercial gasoline in the refinery industry. The protocol and apparatus for acquiring the RVP are well described in ASTM D-323. The RVP is the absolute vapor pressure exerted by a mixture as determined at a temperature of 100˚F (37.8˚C/311.0K) and a vapor to liquid ratio of 4:1. It differs from the true vapor pressure (TVP) which is described as the pressure exerted by a vapor in equilibrium with its liquid phase at a specific temperature. Measuring the TVP is probably more conducive for determining the concentration of combustion contaminants emitted into the atmosphere since a maximum threshold has been imposed for the VP of gasoline in order to restrict air pollution [1] - [3] .

The petroleum industry relies heavily on performing simulations in order to test and optimize processes prior to the manufacturing of gasoline [4] . This is done in order to ensure the gasoline to meet technological specifications and stringent environmental regulations mandated to improve air quality. High quality empirical VP data, as a function of temperature, and thermodynamic information are crucial input parameters for the optimization of these models. The enthalpy of vaporization (∆H_vap) is one of these vital thermodynamic parameters since it is one of several characteristics that describe the volatility of a fuel. Predicting the amount of heat required to evaporate (i.e. vaporizes) a specific quantity of gasoline to produce an ignitable air-fuel-vapor mixture is of the utmost importance for automobile engines; this is particular important to know before formulation of a gasoline blend and it being released to market [4] . Equally important is the use of analytical equations to produce input parameters for models. These equations also serve to compute stand-alone thermodynamic information of gasoline blends. An excellent outline of numerous analytical expression used in this capacity was summarized by Riazi et al. [3] .

There is a large database of enthalpy of vaporization (∆H_vap) values for pure volatile organic compounds (VOCs). This information can be readily found in reference books such as the CRC (Chemical Rubber Company) Handbook of Chemistry and Physics and Perry & Green Chemical Engineers Handbook. However, there is a lack of ∆H_vap data on complex mixtures such as gasoline and aviation fuel; this may be due to earlier studies not being well developed as suggested by Chapka et al. [5] . Nevertheless, there is a plethora of Reid and true vapor pressure data on numerous blends of gasoline [6] . The Clausius-Clapeyron equation (i.e. plot of lnP vs. 1/T(K)) could be readily applied to this gasoline VP data in order to create preliminary ∆H_vap values as well as construct a database. This precursory information would facilitate filling this particular knowledge gap.

The intent of this study was to amass high quality TVP data of 87 grade gasoline over a series of temperatures, i.e. as a function of temperature. The VP is a crucial physical property that is closely associated with volatility. It can be used to approximate a number of thermodynamic entities. Hence, the gasoline VP data acquired in this work were employed to predict the enthalpy of vaporization (∆H_vap) and compute the entropy of vaporization (∆S_vap). Although the Clausius-Clapeyron is a classic method for calculating ∆H_vap of pure liquids, it is well suited for this investigation. VP data were also acquired for n-heptane and n-octane in order to optimize the performance of this novel VP acquisition system and concomitantly serving as references data. This type of meticulous evaluation is necessary to ensure the reliability of the methodology and empirical results generated from this novel system. The VP data (water, ethanol, and toluene) and the computed thermodynamic data presented in an earlier paper are incorporated in this investigation due to coinciding data collection intervals [7] .

2. Experimental

2.1. Materials

The gasoline sample used in this work was purchased at a local Sunoco gas station, and had an octane rating of 87. The composition and information on the ingredients of the gasoline are listed on its material safety data sheet. The VOCs n-heptane (99% HPLC grade), n-octane, anhydrous ethanol (EtOH), toluene were purchased from the Aldrich Chemical Company and Fischer Scientific. These materials, gasoline and chemicals, were used without purification and handled using proper safety measures as specified from their Material Safety Data Sheet.

2.2. Methodology

The VP data of gasoline along with n-heptane (99% HPLC grade), n-octane, distilled water, EtOH, and toluene was measured utilizing an enhanced VP acquisition system, which is an innovative modification of the “Boiling-Point Method” apparatus. In this procedure, liquid vapors are in equilibrium with its boiling liquid at a specific externally applied pressure. The method is well recognized in the literature [8] . A portable Welch GEM direct-drive vacuum pump was used as the external vacuum source to vary the pressure of the acquisition system. A digital vacuum regulator (DVR) manufactured by J-KEM Scientific, connected to the vacuum pump, was utilized to accurately control the pressure (±0.5 torr) above the gasoline sample (100 ml) in the liquid reservoir (250 ml round-bottom flask).

The heating of the gasoline sample was carried out using a Büchi model B-490 water bath interfaced with a J-KEM Scientific digital temperature controller (DTC). The liquid reservoir was submerged in the water bath to equilibrate the sample at a predetermined set temperature in which the VP would be measured. The temperature of the sample was measured by the thermocouple sensor component (±0.5˚C) of the DTC, which was positioned in the middle of the sample. The DVR and DTC were interfaced to a desktop PC, which logged into an excel spreadsheet the temperature and pressure data in real-time every 20 seconds. The resulting VP data can be readily evaluated in the excel spreadsheet or exported for processing using the KaleidaGraph software package. A minimum of nine VP measurements were acquired at each specified temperature to ensure reproducibility of the data; this would correspond to a total minimum acquisition time of three minutes. There were between nine and 30 VP measurements acquired at each temperature interval throughout this investigation. The standard deviation in pressure (torr) and temperature (C) is shown in Table 1 for water and the each VOC. These units of temperature and pressure were chosen to be consisted with the literature in which they were compared. A detailed illustration of the enhanced VP acquisition system was depicted in a prior publication in this journal [7] .

3. Result and Discussion

In this investigation, the enhanced VP acquisition system was used to collect empirical VP data of Sunoco 87 grade gasoline, n-heptanes, and n-octane. Calibration of the system using distilled water, EtOH, and toluene have also been reported. The information also served as a reference indicator, and is displayed with all the results of this investigation in Table 1. It can be readily observed that the experimental data is inline with the literature data [9] , which are shown in parentheses in Table 1.

Determining the vapor pressure of a pure liquid or mixture is rooted in understanding the existence of a liquid-vapor boundary. A dynamic equilibrium exists between the two phases, i.e. the liquid and vapor phases; this is an interface in which the pressures and temperatures of the two phases can co-exist. The Clapeyron equation is an exact expression for the slope of the liquid-vapor phase boundary. Equation (1) represents the equilibrium that occurs between the liquid-vapor phases, where the slope of the boundary is dP/dT:

(1)

In this equation, ΔH_vap is the change in the enthalpy of vaporization and T is the absolute the temperature in Kelvin. The variable ΔV_vap correspond to the change in molar volume of vaporization, where we assume the gas phase behaves as an ideal gas. If we infer that ΔV_vap ≈ V_vap and use the ideal equation of state, we can derive Equation 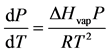(2):

(2)

The variable P in Equation (2) is the vapor pressure and R is the gas constant (8.314 J/mol∙K). By separating the variables P and T, integration of Equation (2) yields the Clausius-Clapeyron equation; this well known phase equilibrium expression is repre- sented by Equation (3)

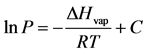(3)

The enthalpy of vaporization can be predicted from Equation (3) from a plot of the natural logarithm of pressure (lnP) versus the reciprocal absolute temperature (1/K). A straight line is generated with a slope equal to −ΔH_vap/R and an intercept denoted by the constant C [8] . This is the methodology employed in this study to predict ∆H_vap Equally, the value of ∆S_vap for each liquid was computed using Trouton’s Law and is expressed by Equation 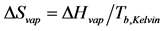(4):

(4)

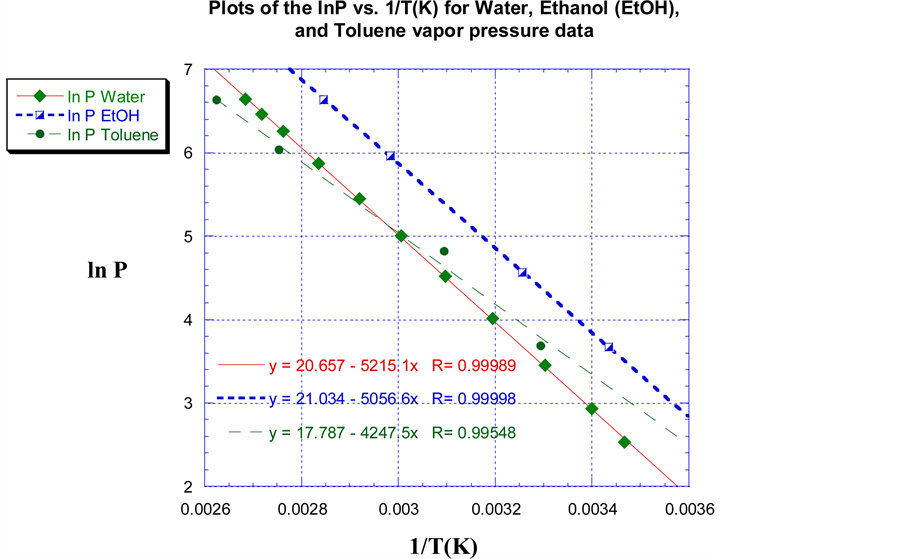
Figure 1 illustrate plots of the empirical VP data of the calibration and reference liquids water, EtOH, and toluene as the lnP vs. 1/T(K). A linear least square regression fit was applied to each set of VP data and is depicted in Figure 1. Using the water VP data as an example, a linear least square regression fit of the data results in an equation for the line of best fit equal to y = 20.657 − 5215.1x. This can be translated to the form of Equation (5) as:

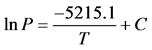(5)

The enthalpy of vaporization (∆H_vap) and entropy of vaporization (∆S_vap) of the reference liquids were determined prior to that of the 87 grade gasoline. This was completed in order to acquire the optimal VP data as well as ensure maximum performance of the VP acquisition system. Using the slope of the linear square regression fit of the water VP data, a value of 43.4 kJ∙mol⁻¹ was evaluated as the enthalpy of vaporization (∆H_vap) of water; this deviated by approximately 1.0% from the literature value [9] . The entropy of vaporization was determined using Equation (4) (Trouton’s Law) by dividing ∆H_vap of water by its normal boiling point temperature in Kelvin (100.0˚C, 373.2 K); this resulted in a ∆S_vap of 116.3 J/mol∙K for water. The predicted values of ∆H_vap for EtOH and toluene were 42.0 kJ/mol and 35.3 kJ/mol respectively using the line of best fit through the empirical VP data. The ∆H_vap of EtOH and toluene deviated by 1.0 and 5.4% respectively, and were in excellent agreement with the literature [9] . The computed values for ∆S_vap of EtOH and toluene were 119.5 J/mol∙K and 35.3 J/mol∙K respectively. Although this data is from a previously published study by the authors, the inclusion of it in this paper strengthens and validates the performance as well as the use of the enhanced VP acquisition system.

The VP measurements were obtained for Sunoco 87 grade gasoline. The data was subsequently used to predict the ΔH_vap and ∆S_vap of the fuel. These thermodynamic entities were predicted in the same manner as the water and VOCs references. A linear least square fit of the gasoline VP data resulted in a slope of −4223.3 as shown in Figure 2; this produced a ∆H_vap of 35.1 kJ/mol and ∆S_vap of 102.5 J/mol∙K. The normal boiling point of the gasoline was determined to be approximately 69.1˚C (342.3 K). This is the temperature in which the gasoline boiled at approximately 760 torr, i.e. the normal boiling point. The values of ∆H_vap for the two gasoline samples used in the study performed by Balabin et al. were 37.3 kJ/mol and 35.4 kJ/mol [10] . These values com- pare favorable to the result of 35.1 kJ/mol predicted in this investigation. This clearly indicates the viability and efficiency of the enhanced VP acquisition system for

amassing VP data.

VP data was also amassed for n-heptane and n-octane in this study. Heptane was selected since it is used along with iso-octane to alter the octane rating of gasoline blends. In 1927, the octane rating was developed in order to control spontaneous combust of gasoline blends that produce a knocking sound in a standard engine. The straight n-heptanes caused severe knocking in an engine and assigned a rating of 0. In contrast, iso-octane (2,2,4-trimethylpentane) was assigned an octane rating of 100 since it did not cause knocking in engines [11] . During this investigation, VP measurements were acquired for n-octane (octane rating of −20) due to the lack of iso-octane.

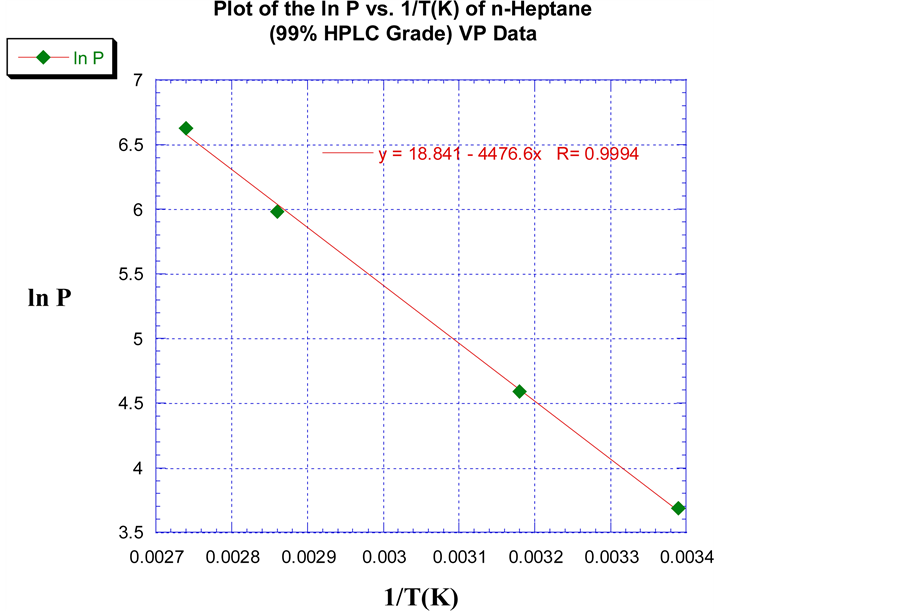
The values for ∆H_vap and ∆S_vap for n-heptane and n-octane were predicted and computed in the same manner as the Sunoco 87 grade gasoline. An 87 octane gasoline can be described as having the knock resistance as a mixture of 13% n-heptane and 87% iso-octane by volume (v/v) respectively. In Figure 3, the linear least square regression fit of n-heptane yielded a slope of −4476.6 with a correlation coefficient (R) of 0.9994. A value for ∆H_vap of 37.2 kJ/mol was predicted, and a ∆S_vap of 100.1 J/mol∙K was computed using Trouton’s Law. These values were within 3.5% of the literature values [12] . For n-octane, a least square fit of the VP data as shown in Figure 4 resulted in a slope of −4698.8 and a correlation coefficient of 0.99935. A value of 39.1 kJ/mol for ∆H_vap was predicted, and a ∆S_vap value of 98.3 J/mol∙K resulted from this information. Both of these values were within 1.0% of their literature value [13] .

A linear square regression fit was also applied to literature VP data of iso-octane [7] . This plot is shown in Figure 4 along with n-octane linear square regression fit of its empirical VP data. By examining the plots, it is readily apparent that the experimental and literature data do not overlap. However, the two lines are parallel yet their slopes are different; this indicates that two distinct values of ΔH_vap and ∆S_vap for n-octane and iso-octane (2,2,4-trimethylpentane) will be predicted and calculated. An enthalpy of vaporization (ΔH_vap) value of 36.4 kJ/mol was predicted from the linear least squares fit of the iso-octane literature data. The ∆S_vap for iso-octane 97.8 J/mol∙K was computed from the literature. These values were within 3.5% when compared to the study by Wu et al. [14] [15] .

Table 1 is a summation of the VP data amassed for water, EtOH, n-heptane, n- octane, toluene, and Sunoco 87 grade gasoline. It contains the predicted value of ∆H_vap, the computed values of ∆S_vap, the slope of the line fit, and the correlation coefficient. It is important to notice that the correlation coefficient R for all of the linear least square regression fits are close to the value 1. From Table 1, it is readily apparent that the experimental data parallels the literature data, which are shown in parentheses. The results of this investigation clearly demonstrate the exceptional capability and efficiency of our enhanced VP acquisition system for amassing VP data. We believe that this considerable body of original VP data would be invaluable to the petroleum industry since simulations of ΔH_vap are utilized extensively for evaluating and the optimization of processes in the manufacturing of gasoline blend [4] [16] .

4. Conclusion

Vapor pressure data were obtained for 87 grade gasoline using the enhanced VP acquisition system described in this work. VP measurements were also acquired for n-hep- tane and n-octane, which served as reference and system calibration data. The VP data were also used to predict the enthalpy (∆H_vap) and entropy of vaporization (∆S_vap) of these VOCs from their line fits using the Clausius-Clayperon equation and Troutons Law respectively. The VP data and the predicted as well as calculated thermodynamic results were in excellent agreement with the literature results. This work has reinforced the validity and practicality of the enhanced VP acquisition system as an efficient tool.

Acknowledgements

The authors acknowledge Howard University, Dr. Clarence Lee (Executive Director) of the Howard University LS-AMP (Louis Stokes Alliance for Minority Participation) Program, Marquia Whitlock (LS-AMP Program), Monique Yvette McClung (LS-AMP Program), NSF (Grant Number HRD-1000286), and NIH-NIGMS (Grant Number T34GM105660).

Cite this paper

Abernathy, S.M. and Brown, K.R. (2016) Predicting the En- thalpy of Vaporization and Calculating the Entropy of Vaporization of 87 Octane Gaso- line Using Vapor Pressure. Open Access Li- brary Journal, 3: e2954. http://dx.doi.org/10.4236/oalib.1102954

References