Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70331,6 pages
10.4236/opj.2016.68B035
Measuring Method of Radius of Curvature Based on Dual-Frequency Laser Interferometer
Wenlong Zhang, Liang Miao, Yu Liu
State Key Laboratory of Applied Optics, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun, China



Received 26 July 2016; accepted 22 August 2016; published 25 August 2016

ABSTRACT
In order to achieve high-accuracy measurement of radius of curvature of optical sphere, ultra-high accuracy radius of curvature testing device is developed by dual-frequency laser interferometer and Fizeau interferometer based on cat’s eye and confocal method. Through analyzing the error source models of radius of curvature testing, optical configuration of the testing device has been optimized. Precise environment control and real-time monitoring system is also established to reduce the errors caused by environment. Through the above processes, the radius of curvature measurement relative accuracy is better than 2 ppm. One optical sphere, R88.5 mm, test aperture 59 mm, has been tested. Testing result is 88499.465 ± 0.176 μm, meeting the design requirement. The method has high accuracy and practical advantages.
Keywords:
Radius of Curvature, Cat’s Eye and Confocal Method, Dual-Frequency Laser Interferometer

1. Introduction
For high precision spherical optical elements are widely used in the fields of lithography, metrology, inertial confinement fusion, synchrotron radiation, etc., measurement accuracy requirements of radius of curvature of optical sphere continue to increase. High accuracy measuring technology of radius of curvature has important significance and application prospects [1] [2].
There are several methods of measuring radius of curvature, including spherometer, mechanical measurement by a Coordinate Measuring Machine (CMM), cat’s eye and confocal method, laser tracker with laser interferometer method and so on. Spherometer has low relative accuracy about 3 × 10−4 [3]-[4]. CMM has a relative accuracy about 4× 10−6, but there is the risk of scratches due to contact measurement. Laser tracker with laser interferometer method is always used in low accuracy and large radius of curvature measurement. Cat’s eye and confocal method based on dual-frequency laser interferometer and Fizeau interferometer is suitable for high precision applications since it is non-contact and high accuracy [5]-[7].
High-accuracy testing device measuring radius of curvature based on cat’s eye and confocal method is described in this paper. The testing device is developed based on dual-frequency laser interferometer and Fizeau interferometer. By analyzing the error source models of radius of curvature testing, optical configuration design of the testing device has been optimized. Precise environment control and real-time monitoring system is also established to reduce the errors caused by environment. Compared with other non-contact radius of curvature test methods, the method used in this paper has high accuracy and practical advantages.
2. Measuring Program of Radius of Curvature and Error Analysis
In this method, a figure measuring interferometer (a phase measuring interferometer, or PMI) is employed to identify the null positions at the center of curvature (confocal) and surface (cat’s eye) of the test optical sphere. The power of the interferometric results is zero at those two positions. Move the test optic from cat’s eye to confocal, called Z-direction. The dual-frequency laser interferometer (a displacement measuring interferometer, or DMI) is employed to identify the movement. The radius of curvature of the test optical sphere is equivalent to the Z-direction distance between cat’s eye and confocal (Figure 1).
The main measuring error sources include: 1) cat’s eye-confocal positional error, 2) test area error, 3) deadpath, 4) unsensed length, 5) cosine error, 6) DMI error, 7) PMI transmitted wavefront error, 8) error caused by the figure error and aperture variation.
2.1. Cat’s Eye-Confocal Positional Error
Important characteristic of cat’s eye-confocal positions is that the result of interferometric result defocus (Power) is zero. Environmental changes between interferometric cavity will reduce the test repeatability of defocus. Z-position of test optic is linear proportional to defocus around cat’s eye and confocal. As in Equation (1),
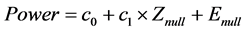 (1)
(1)
where  is the constant term,
is the constant term, 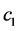 is the slope of defocus with Z-direction displacement.,
is the slope of defocus with Z-direction displacement., 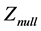 is Z-position of test optic,
is Z-position of test optic, 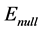 is defocus variation caused by environmental changes. Cat’s eye-confocal positional error could be represented as
is defocus variation caused by environmental changes. Cat’s eye-confocal positional error could be represented as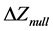 ,
,
 (2)
(2)
Due to cat’s eye-confocal positional error varies when the environment changes, it could be achieved by statistical analysis. It is type A uncertainty. In this paper the measuring environment is well controlled, the cat’s eye-confocal positional error is estimated about 0.120 μm.
2.2. Test Area Error
Test area means the space between cat’s eye and confocal positions. Environmental changes will cause the variation of refractive index of test area. Test area error is represented as Equation (3),
Figure 1. Schematic of cat’s eye and confocal method for radius of curvature measurement.
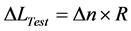 (3)
(3)
where 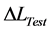 is test area error,
is test area error, 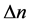 is variation of air refractive index,
is variation of air refractive index, 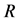 is the length of test area.
is the length of test area. 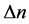 is calculated by Edlen formula [8] [9],
is calculated by Edlen formula [8] [9],
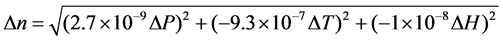 (4)
(4)
where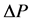 ,
, 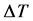 ,
, 
2.3. Deadpath
Deadpath is the nearest Z-distance between test corner cube and reference corner cube. Deadpath error is caused by the variation of air refractive index.

where 



2.4. Unsensed Length
The Z-distance between test optical sphere and test corner cube, and the Z-distance between reference corner cube and transmission sphere (TS lens) are unsensed length. The mechanism located in unsensed length will have a thermal expansion when temperature changes.





2.5. Cosine
If the laser beam is not exactly parallel with the direction of motion, a proportional difference increases with the measurement distance is established between the actual path length and the measured length. It is type B uncertainty.

where 





2.6. DMI Error
In order to reduce DMI error, high precision dual-frequency laser interferometer should be used. DMI error includes type A and type B uncertainties. But type B uncertainty is major factor. According to the dual-frequency laser interferometer which is used, laser wavelength error (±0.1 ppm) and wavelength stability (±0.02 ppm), sub-divisional error (1.2 nm) and DMI internal alignment error (2.2 nm),

the DMI error DLDMI is about 0.009 μm.
2.7. PMI Transmitted Wavefront Error
This error exists, because the transmitted wavefront from PMI is not ideal.PMI transmitted wavefront error is mainly from TS lens, whose transmitted wavefront is better than 0.5λPV (λ = 632.8 nm) in this paper. Through analysis of test model in optical software Zemax, 
2.8. Figure Error and Aperture Variation
Since the figure error of test surface, the PMI wavefront will not focus on the best fit sphere of test surface at cat’s eye position. And when the test aperture changes, the radius of curvature of best fit sphere varies. The error 
2.9. Uncertainty Analysis of Radius of Curvature Testing Device
After analyzing the error source models from 2.1 to 2.8, the optical configuration design is optimized to reduce measurement errors. The testing device is developed as shown in Figure 2. There are two kinds of measurement errors, type A uncertainty and type B uncertainty. The type A uncertainty includes cat’s eye-confocal positional error, test area error, deadpath, unsensed length. The type B uncertainty includes cosine error, DMI error, PMI transmitted wavefront error, error caused by the figure error and aperture variation. Abbe error is negligible.

The type A uncertainty of the testing device is calculated by Equation (10) as 0.176 μm.

The type B uncertainty of the testing device is calculated by Equation (11) as 0.045 μm.

The combined uncertainty is 0.182 μm as Equation (12).
Hence, the testing device’s combined uncertainty is 0.182 μm when measuring the test sphere (R88.5 mm, test aperture 59 mm), relative accuracy is estimated as 2 ppm.
3. Experiment of Radius of Curvature Measurement
3.1. Measurement Procedure
Adjust the direction of movement of the test optic, parallel with the PMI’s and DMI’s optical axis (0.5 mrad)
Move the test optic to cat’s eye position, then adjust TS to keep zero fringe pattern of PMI and set the three DMI zero.
Move and adjust the test optical sphere to confocal position, keep zero fringe pattern of PMI, record the three DMI results and calculate average value. Average value is the nominal radius of curvature need to be tested.
According to the barometric pressure, temperature and humidity value, get the real air refractive index. Then remove the error caused by variation of air refractive index, the real value of radius of curvature is achieved.
3.2. Experiment Result
Nine testing results of the radius of curvature of test optical sphere R88.5 is shown as follows (Table 1).
The type A uncertainty is 0.170 μm by statistical calculation. The testing result agrees with the analysis of error sources model in Chapter 2. Feasibility of optimizing optical configuration is verified. According to the analysis of type B uncertainty above, the combined uncertainty is shown as Table 2.
In summary, the testing result of the radius of test sphere R88.5mm is 88499.465 ± 0.176 μm, relative accuracy is 2 ppm (confidence level 95%).
4. Conclusion
In order to achieve high accuracy radius of curvature measurement, cat’s eye and confocal method based on dual-frequency laser interferometer is investigated. The radius of curvature testing device is developed, combining DMI, PMI and precise environment control and real-time monitoring system. The measurement error
Figure 2. Testing device for R88.5.
Table 1. Testing result of the radius of curvature of test sphere R88.5.
Table 2. Analysis of the radius testing accuracy of test sphere.
source models are established and analyzed to guide optimizing optical configuration. The radius of curvature of test sphere R88.5 mm, test aperture 59mm is tested. The relative accuracy is 2 ppm, meeting the design requirement. In this paper, the core idea of the radius of curvature test method is to create all the test error source analysis models and to optimize testing device optical configuration for different test optics so that each source of error is minimized and ultra-high accuracy measurement of radius of curvature is achieved.
Acknowledgements
I would like to extend my sincere gratitude colleague Jie Yu, Hui Wang and Benyin Guo. I am deeply grateful of their help and instructive advice in the completion.
Cite this paper
Wenlong Zhang,Liang Miao,Yu Liu, (2016) Measuring Method of Radius of Curvature Based on Dual-Frequency Laser Interferometer. Optics and Photonics Journal,06,209-214. doi: 10.4236/opj.2016.68B035
References
- 1. Seitz, G., Schulte, S., Dinger, U., et al. (2004) EUV-Microlithography—A Challenge for Optical Metrology. SPIE, 5533, 20-26. http://dx.doi.org/10.1117/12.556317
- 2. Takigawa, Y., Nakayama, S., Yamamoto, T., et al. (2005) Absolute Accu-racy Evaluation of a Spherical Null Testing for EUVL Mirrors. SPIE, 5869, 58690Q-1-58690Q-11.
- 3. Peng, S.J. and Miao, E.L. (2014) Sub-Micron Precision Measurement of Radius of Curvature and Uncertainties Analysis. Acta Optical Sinica, 34, 0512001-1-0512001-8. (In Chinese)
- 4. Chen, L. (2005) The Research of Single Frequency Laser Interference for Spherical Radius of Curvature Measurement. Nanjing University of Science and Technology, Nanjing. (In Chinese)
- 5. Schmitz, T.L., Davies, A.D. and Evans, C.J. (2001) Uncertainties in Interferometric Measurements of Radius of Curvature. SPIE, 4451, 432-447.
- 6. Sun, R.D., Qiu, L.R., Yang, J.M., et al. (2011) Development of Laser Differential Confocal Radius Measurement System. Chinese Journal of Scientific Instrument, 32, 2833-2838. (In Chinese)
- 7. Tian, Z.H., Shi, Z.G., Liu, W.Q., et al. (2013) High-Accuracy Measurement for Radius of Curvature and Its Uncertainties. Optics and Precision Engineering, 21, 2495-2501. (In Chinese) http://dx.doi.org/10.3788/OPE.20132110.2495
- 8. Sha, D.G. (2003) Analysis of Measurement Error and Evaluation of Measurement Uncertainties. Chinese Metrology Press, Beijing. (In Chinese)
- 9. Bobroff, N. (1993) Recent Advances in Displacement Measuring Interferometry. Measurement Science and Technology, 4, 907-926. http://dx.doi.org/10.1088/0957-0233/4/9/001




