Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70325,8 pages
10.4236/opj.2016.68B029
Analysis and Investigation of Slow Light Based on Plasmonic Induced Transparency in Metal-Dielectric-Metal Ring Resonator in a Waveguide System with Different Geometrical Designs
Mehdi Hassani Keleshtery1, Hassan Kaatuzian2, Ali Mir1
1Electronics Group, Faculty of Engineering Department, Lorestan University, Khorramabad, Iran
2Photonics Research Laboratory (PRL), Electrical Engineering Department, Amirkabir University of Technology, Tehran, Iran



Received 26 June 2016; accepted 18 August 2016; published 25 August 2016

ABSTRACT
In this paper we will try to create, propose and analyze structure of a slow light device, based on plasmonic induced transparency in a metal-dielectric-metal based ring resonator. Group index by first design about 37 and second design about 35 earned. The proposed dielectric material is Poly Methyl Meta Acrylate (PMMA) sandwiched by gold metal cladding. Finite Element Method-con- ducted Electromagnetic simulations are employed to evaluate the plasmonic designs for behavior of slow light. The signal and pump wavelength are assumed to be 830 nm and 1550 nm respectively in the systems. The overall length of the plasmonic slow light system is 600 nm. In a wide range of frequency bands, the optical properties of metals can be described with a plasma model. The optical signal can be achieved with the use of surface waves on the boundary between the insulating materials and metals with dimensions smaller than the diffraction limit. The main goal, is estimation of optical characteristics such as bandwidth, the Real and Imaginary parts of refractive index, group velocity and slow down factor in such optical devices. The obtained results and observations, can be useful in basic research and the production of highly integrated plasmonic devices.
Keywords:
Slow Light, Plasmonic Induced Transparency, Metal-Dielectric-Metal, Poly Methyl Meta Acrylate (PMMA), Surface Plasmon Polaritons, Refractive Index, Slow Down Factor

1. Introduction
In photonics technology, there’s an important sub-branch, called Plasmonics [1]-[5]. Plasmonics, as an alternative platform for manipulating and redirecting electromagnetic waves on metal surfaces [2] [4], is based on surface Plasmonpolaritons (SPPs) [3] [6], where the light coupled with electrons in metal-dielectric interface [7].
Because of overcoming the conventional optical diffraction limit and manipulation of optical wave in nano- scalefield [8], SPPs have the potential for realizing highly integrated optical circuits [9]-[11]. Many applications can be found in this area. For instance, optical sensors [12], bend waveguide devices [13], wavelength de-mul- tiplexers [14], filters [15], plasmonic switches and amplifiers [14]-[16], nano-wires, slow light devices [17], etc… .
Electromagnetically Induced Transparency (EIT) is the result of quantum interference in a three-level atomicsystem [7] [15]. The Plasmon Induced Transparency (PIT), is a plasmonic analogue of EIT [17]. The main characteristics of PIT lie in the appearance of a sharp and symmetric transparency window within absorption band, along with extraordinary steep dispersion and a dramatic reduction in group velocity [8] [18]. In this study, two designs have been proposed to display PIT in plasmonic nano-structures. Among those designs, the resonators side coupled to the metal-dielectric-metal (MDM) waveguide are of special interests, since the PIT effect can be realized in plasmonic integrated circuits [19]. In this paper, we’ve tried to design, simulate and analyze (1*1) and (1*2) MDM single ringresonators proposed slow light devices.
After this introduction section, in Section 2, we’ll have events analysis in plasmonic resonators, in which we’ll describe in details the structure of our proposed circular metal-dielectric-resonator in micron scale. The theory has been reviewed in Section 3. Simulation results of two different proposed slow light devices will be reported in Section 4. We’ll also have a conclusion section.
2. Analysis of Events in Plasmonic Resonators
Induction plasmonic modes creates transparency in structures to reduce speed of light (signal). For induction creation, secondary powerful light (pump) is used for stimulation of plasmonics modes formation and deceleration of signal light in waveguide [15]-[20].
Figure 1 demonstrate a simple schematic for plasmon waveguide loaded with dielectric [20]. This plasmanic structure includes a dielectric waveguide with height (h) and width (w) on a metal layer with thickness of (G).
Dielectric layer adjacent to the metal layer can be formed prerequisite for ensuring plasmonic modes there.
Dielectric material in this study is called PMMA with a refractive index close to (n = 1.4) [21]. The layer made from gold or silver that can be selected depending on dielectric material as well as manufacturing conditions.
Other metals such as copper and aluminum as used in conventional electronic and photonic integrated circuits, may also be used [21]-[23].
In conventional photonic ring resonators, basically, two waveguides exists. One for straight waveguide at aside of circular (loop) waveguide. The cross sectional dimensions of waveguides are proportional to light wavelength. We’ve used this concept for designing a plasmonic waveguide resonator in the field of integrated slow light plasmonic device. In Figure 2, the configuration of a plasmonic MDM resonator is shown.
Figure 2 shows basically, a proposed structure for plasmonic waveguide ring resonator. A combination ofplasmonic waveguide loaded with dielectric polarization surface plasmon is designed in micrometer scale. Ascan be seen, a ring plasmonic waveguide is located in close proximity to a straight waveguide [24]. Perfectly circular ring-shaped waveguide with radius R = 5500 nm formed a ring oscillator. The minimum distance between the dielectric two straight and circular waveguide at the contact site in the zero point, assumed to be 159 nm. This distance can be varied depending on the waveguide design. Metal-dielectric-metal plasmonic waveguides has dimensions transverse profile w × h = 600 * 600 nm2, and integrated gold metal film thickness G =
Figure 1.Schematic diagram of the composition of the surface plasmon waveguide loaded with dielectric polarization.
Figure 2. Schematic diagram of the proposed circular metal-dielectric resonator structure. Dimension of this design is the micrometer scale.
100 nm. Beam waveguide ring oscillator according to the desired operating frequency range of all-optical wave length λ = 1550 nm equal R = 5500 nm is considered. The light wave as a pump for exciting the environment and create transparency in the proposed structure is used. In this study, the imaginary part of the refractive index, real part of the refractive index and slow rate of change in film thickness of metal in a metal-dielectric-metal waveguide system are estimated. The change in the radius of the ring resonator, the electromagnetic wave in this element will have a direct impact on the response of slow light device [25] [26].
3. Theory of Plasmonic Resonator System
SPPs, are surface electromagnetic modes that propagate at the interface of a dielectric with real electic permittivity and a metal with negative permittivity. According to Drude model, we’ll have:
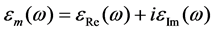 (1)
(1)
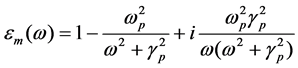 (2)
(2)
In the above formula, ω is the angular frequency, ωp = 1.38 × 1016 Hz, is bulk plasmon frequency and γp = 2.73 × 1013 Hz is loss absorption coefficient [7] [27]. We know that the surface plasmon polariton waves do not propagate in TE mode. There is only TM waves that can be published in plasmonic structures.
Therefore, using the governing equations for electromagnetic waves at the interface between the metal-dielec- tric interface in accordance with the continuity equation, the following relations are required:
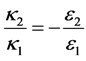 (3)
(3)
Complex wave vector  of surface plasmon polaritonin metal-dielectric-metal waveguide with width of W is defined on the basis of the value of the effective refractive index [28].
of surface plasmon polaritonin metal-dielectric-metal waveguide with width of W is defined on the basis of the value of the effective refractive index [28].
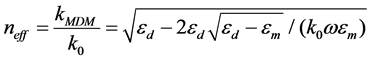 (4)
(4)
where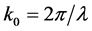 , is the wave vector in free space and εd and εm are permittivity for dielectric and metal constant, and kd is the transverse wave number in the dielectric core and km is the transverse wave number of metal cladding [27]-[29]. So we’ll have:
, is the wave vector in free space and εd and εm are permittivity for dielectric and metal constant, and kd is the transverse wave number in the dielectric core and km is the transverse wave number of metal cladding [27]-[29]. So we’ll have:
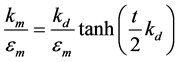 (5)
(5)
In the specific area of frequency, using the following formula, metals, are the most absorbent.
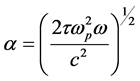 (6)
(6)
Applying the Bear’s Law of attraction implies that for some low frequencies, the field penetrates with a factor of 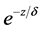 into metal where
into metal where 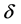 is skin depth. In low-frequency behavior according to the Boltzmann transport
is skin depth. In low-frequency behavior according to the Boltzmann transport
equation, it suggests that the above description is valid until that the average electron distances are 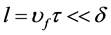 that
that 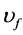 is Fermi velocity [10] [22]. At room temperature, for conventional metals
is Fermi velocity [10] [22]. At room temperature, for conventional metals  and
and 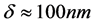 therefore the free electron model justifies [28].
therefore the free electron model justifies [28].

From Equation (7) we can quantitatively and clearly the forming of PIT phenomenon: as incident optical waves transmit into this system. The coupling coefficient between the two ways in our design is denoted by γ. The small nanodisk coupled to a waveguide for d = 159 nm, can be treated as an oscillator and the cavity mode decays equally into the propagating waveguide, β is the coupling coefficient between them. 
frequency of the nanodisk.
4. Simulation Results in Two Different Geometrical Designs
Signal Transmission T, as a function of variations of refractive index is depicted in Figure 3. This diagram is according to our proposed circular metal-dielectric resonator structure. “S” and “L”, are electromagnetic wavesspreading through straight and ring waveguides [17] [23].
4.1. Arranged MDM Single Ring Resonator 1 × 1
According to schematic diagram of Figure 2, for our 1 * 1 proposed circular metal-dielectric resonator, we started to simulate the behavior of this micron order PIT slow light device. Figure 4 shows the numerical simulation results of a ring oscillator (radius R = 5 μm) based slow light device. Absorption, refractive index, slow down factor and transmission curves are all depicted in Figure 5 and Figure 6 as functions of wavelength.
4.2. Arranged MDM Single Ring Resonator 1 × 2
In the second proposed design, we have a 1 * 2 ring resonator slow light device. It has one input and two outputports. Like Figure 7 Absorption, refractive index, slow down factor and transmission curves are all depicted in Figure 8 and Figure 9 as functions of wavelength. Similar plasmonic ring resonator describe in previous section, including a ring oscillator polarization surface plasmon waveguide structure with dielectric loaded with radius R = 5 μm. Plasmonic waveguide structure similar to that in the middle of a place is split into two output ports of the elements together [25]. The ring oscillator output ports with numbers 1 (located at the output end of
Figure 3. Schematic diagram of the proposed circular metal-dielectric resonator structure.
Figure 4. Numerical simulation of the ring oscillator-based slow light to show through the wave plasmonic cross from the waveguide coupling with oscillating wave.Dimension of this design is the micrometer scale.
Figure 5. The absorption coefficient (imaginary part of the refractive index) in various thicknesses of metal films (G) in metal-dielectric-metal waveguide structure is proposed (Left picture). The real part of the refractive index of the film in various thicknesses of metal films (G) in metal-dielectric-metal waveguide structure is proposed (Right picture).
Figure 6. The slow down factor (SDF) in various thicknesses of metal films (G) in metal-dielectric-metal waveguide structure is proposed (Left picture). Transmission range of the proposed project for the normalized curve is displayed. The whole thickness of 100 nm thick gold metal in the structure of MDM is presented (Right picture).
the straight waveguide) and 2 (located at the end of the waveguide port connections) are numbered. Straight waveguide element distance d = 250 nm lips with a lip of the ring oscillator passes.
Figure 7. The results of the simulation of a proposal for adevice based on slow light that includes a ring oscillator and a thumbnail image contained in this form, coupled plasmonic mode shows the structure of MDM, have two output port that shown. Dimension of this design is the micrometer scale.
Figure 8. The absorption coefficient (imaginary part of the refractive index) in various thicknesses of metal films (G) from output 2in metal-dielectric-metal waveguide structure is proposed (Left picture). The real part of the refractive index of the film in various thicknesses of metal films (G) from output 2 in metal-dielectric-metal waveguide structure is proposed (Right picture) from port of output No. 2 shows that in Figure 7.
Figure 9. The slow down factor (SDF) in various thicknesses of metal films (G) from output 2 in metal-dielectric-metal waveguide structure is proposed (Left picture). Transmission range of the proposed project for the normalized curve is displayed. The whole thickness of 100 nm thick gold metal in the structure of MDM is presented (Right picture) from port of output No. 2 shows that in Figure 7.
5. Conclusions
This paper presents numerically-conducted study around two new MDM-based plasmonic ring resonators in field of slow light to be designed and investigated. The proposed compact configuration as a symmetric and non-symmetric waveguide-structure is engineered.
In general, using plasmonic waveguides as alternatives for photonics devices that have been designed and built based on conventional dielectric waveguides have the advantage of obtaining much smaller sizes (up to several thousand times smaller).
However, their advantage at the expense of effective distance publish or in other words increase the release will be casualties. The wavelength of the incoming light wave as a signal in this investigation is considered to be equal to 830 nm and also transparent to pump wavelength of 1550 nm affecting the proposed structure is calculated. Plasmonic devices, propose higher speeds with lower density and power consumption than their photonic or electronic counterparts. As a result of investigations, the effects of PIT in the ring resonator design of the waveguide system with MDM, showed good agreement between transport phenomena and dispersion in the window transparency. SDF obtained at two proposed design are estimated to be more than 35.
Finally, diffusion constants derived for a system indicated that in the transparency of the window, the proposed structure can be easily adjusted by changes in metal film thickness. We also found that the resonance quality factor, can effectively adjust the dispersion relation. These plasmonic systems can be used as a hight performance filter. The default settings are made in fundamental research and applications for building integrated plasmonic devices useful. These novel plasmonic systems have important potential applications in optical nonlinearity enhancements, all-optical signal processing applications, optical communication and nonlinear devices.
Acknowledgements
The authors would like to thank their colleagues in P.R.L of Amirkabir University of Technology (AUT) for their cordial support.
Cite this paper
Mehdi Hassani Keleshtery,Hassan Kaatuzian,Ali Mir, (2016) Analysis and Investigation of Slow Light Based on Plasmonic Induced Transparency in Metal-Dielectric-Metal Ring Resonator in a Waveguide System with Different Geometrical Designs. Optics and Photonics Journal,06,177-184. doi: 10.4236/opj.2016.68B029
References
- 1. Zia, R., Schuller, J.A., Chandran, A. and Brongersma, M.L. (2006) Plasmonics: The Next Chip-Scale Technology. Mater. Today, 9, 20-27. http://dx.doi.org/10.1016/S1369-7021(06)71572-3
- 2. Atwater, H.A. (2007) The Promise of Plasmonics. Sci. Am., 296, 56-62. http://dx.doi.org/10.1038/scientificamerican0407-56
- 3. El-Kareh, B. (1995) Fundamentals of Semiconductor Processing Technology. Kluwer Academic.
- 4. Barnes, W.L., Dereux, A. and Ebbesen, T.W. (2003) Surface Plasmon Subwavelength Optics. Nature, 424, 824-830.
- 5. Gauthier, D.J., Gaeta, A.L. and Boyd, R.W. (2006) Slow Light: From Basics to Future Prospects. Photonics Spectra, 40, 44-50.
- 6. Khurgin, J.B. and Tucker, R.S. (2009) Slow Light Science and Applications. CRC.
- 7. Hu, M., Wang, F.Q., Liang, R.S., Zhou, S.W. and Xiao, L.P. (2015) Plasmonic-Induced Transparency Based on Plasmonic Asymmetric Dual Side-Coupled Cavities. Elsevier Physics Letters A, 379, 581-584. http://dx.doi.org/10.1016/j.physleta.2014.12.011
- 8. Han, Z.H. and Bozhevolnyi, S.I. (2011) Plasmon-Induced Transparency with Detuned Ultracompact Fabry-Perot Resonators in Integrated Plasmonic Devices. Optics Express, 19, 3251-3257.
- 9. Ozbay, E. (2006) Plasmonics: Merging Photonics and Electronics at Nano Scale Dimensions. Science, 311, 189-193. http://dx.doi.org/10.1126/science.1114849
- 10. Maier, S.A. (2007) Plasmonics: Fundamentals and Applications. Sprin-ger.
- 11. Jenkins, F.A. and White, H.E. (1981) Fundamentals of Optics. 4th Edition, McGraw-Hill.
- 12. Kaatuzian, H. (2008) Pho-tonics. Vol. 1, 2nd Edition, AUT Press, in Persian.
- 13. Zhang, S., Genov, D.A., Wang, Y., Liu, M. and Zhang, X. (2008) Plas-mon-Induced Transparency in Metamaterials. Phys. Rev. Let., 101, 047401. http://dx.doi.org/10.1103/PhysRevLett.101.047401
- 14. Tassin, P., Zhang, L., Koschny, T., Economou, E.N. and Soukoulis, C.M. (2009) Low-Loss Metamaterials Based on Classical Electromagnetically Induced Transparency. Phys. Rev. Let., 102, 053901. http://dx.doi.org/10.1103/PhysRevLett.102.053901
- 15. Lu, Y., Rhee, J.Y., Jang, W.H. and Lee, Y.P. (2010) Active Manipulation of Plasmonic Electromagnetically-Induced Transparency Based on Magnetic Plasmon Resonance. Opt. Express, 18, 20912-20917. http://dx.doi.org/10.1364/OE.18.020912
- 16. Singh, R., Al-Naib, I.A.I., Koch, M. and Zhang, W. (2011) Sharp Fano Resonances in THz Metamaterials. Opt. Express, 19, 6312-6319. http://dx.doi.org/10.1364/OE.19.006312
- 17. Kekatpure, R.D., Barnard, E.S., Cai, W. and Brongersma, M.L. (2010) Phase-Coupled Plasmon-Induced Transparency. Phys. Rev. Let., 104, 243902. http://dx.doi.org/10.1103/PhysRevLett.104.243902
- 18. Li, Z., Ma, Y., Huang, R., Singh, R., Gu, J., Tian, Z., Han, J. and Zhang, W. (2011) Manipulating the Plasmon-Induced Transparency in Terahertz Metamaterials. Optics Express, 19.
- 19. Kaatuzian, H. (2012) Quantum Photonics, A Theory for Attosecond Optics. Amirkabir University.
- 20. Xu, Y., Zhang, J. and Song, G. (2013) Slow Sur-face Plasmons in Plasmonic Grating Wave Guide. IEEE Photon. Technol. Let., 25, 410-413. http://dx.doi.org/10.1109/LPT.2013.2238667
- 21. Wang, Y., Wang, J., Liu, Ch., Luo, Q., Zhang, W. and Gao, Sh. (2013) Plasmon-ic-Induced Transparency in Metal-Dielectric-Metal Waveguide Bends. Applied Physics Express, 6, 082201. http://dx.doi.org/10.7567/APEX.6.082201
- 22. Yang, X., Hu, X., Chai, Z., Lu, C., Yang, H. and Gong, Q. (2014) Tunable Ultra-compact Chip-Integrated Multichannel Filter Based on Plasmon-Induced Transparencies. Appl. Phys. Lett., 104, 221114-1-221114-5. http://dx.doi.org/10.1063/1.4882916
- 23. Zhan, Sh., Li, H., Cao, G., He, Z., Li, B. and Yang, H. (2014) Slow Light based on Plas-mon-Induced Transparency in Dual-Ring Resonator-Coupled MDM Waveguide System. J. Phys. D: Appl. Phys., 47, 205101.
- 24. Zhou, Q.Z., He, P., Xu, J., Zhuang, X., Li, Y. and Pan, A. (2014) Gradient Index Plasmonic Ring Resonator with High Extinction Ratio. Opt. Commun., 312, 280-283. http://dx.doi.org/10.1016/j.optcom.2013.09.041
- 25. Kaatuzian, H. and Taheri, A.N. (2015) Application of Nano-Scale Plasmonic Structures in Design of Stub Filters-A Step towards Realization of Plasmonic Switches. INTECH, Book Chapter, Chapter 4. http://dx.doi.org/10.5772/59877
- 26. Kohandani, R. and Kaatuzian, H. (2015) Theoretical Analysis of Multiple Quantum-Well, Slow-Light Devices under Applied External Fields Using a Fully Analytical Model in Fractional Dimension. Quantum Electronics, 45, 89-94. http://dx.doi.org/10.1070/QE2015v045n01ABEH015596
- 27. Keshavarz Moazzam, M. and Kaatuzian, H. (2015) Design and Inves-tigation of N-Type Metal/Insulator/Semiconduc- tor/Metal Structure Two-Port Electro-Plasmonic Addressed Routing Switch. Applied Optics, 54, 6199-6207. http://dx.doi.org/10.1364/AO.54.006199
- 28. Wang, G., Zhang, W., Gong, Y. and Liang, J. (2015) Tunable Slow Light Based on Plasmon-Induced Transparency in Dual-Stub-Coupled Waveguide. IEEE Photonics Technology Letters, 27. http://dx.doi.org/10.1109/LPT.2014.2362293
- 29. Han, X., Wang, T., Li, X., Liu, B., He, Y. and Tang, J. (2015) Dynamically Tunable Slow Light Based on Plasmon Induced Transparency in Disk Resonators Coupled MDM Waveguide System. J. Phys. D: Appl. Phys., 48, 235102.














