Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70312,6 pages
10.4236/opj.2016.68B019
Simulation and Characteristics Improvement of Quantum Dot Slow Light Devices by Geometrical Dimension Alteration
Bahram Choupanzadeh, Hassan Kaatuzian, Reza Kohandani, Saeed Abdolhosseini
Photonics Research Lab (PRL), Electrical Engineering Department, Amirkabir University of Technology, Tehran, Iran



Received 13 June 2016; accepted 18 August 2016; published 25 August 2016

ABSTRACT
In this paper we simulate and analyze a sample of slow light semiconducting device with  quantum dot structure based on coherent population oscillation (CPO). The simulation is conducted to enhance the main parameters of slow light device and a method is presented for setting the output specifications of this kind of devices. In this paper, we deal with changing the size of quantum dot to find the ideal size. The simulation results indicate that as the size of quantum dot changes properly (with reducing more than 50 percent of quantum dots both radius and height), then the slope of diagram of the real part of refractive index increases significantly so that the Slow Down Factor (SDF) predicted to be18 times greater. Analysis and simulations based on cylinderical quantum dots structure
quantum dot structure based on coherent population oscillation (CPO). The simulation is conducted to enhance the main parameters of slow light device and a method is presented for setting the output specifications of this kind of devices. In this paper, we deal with changing the size of quantum dot to find the ideal size. The simulation results indicate that as the size of quantum dot changes properly (with reducing more than 50 percent of quantum dots both radius and height), then the slope of diagram of the real part of refractive index increases significantly so that the Slow Down Factor (SDF) predicted to be18 times greater. Analysis and simulations based on cylinderical quantum dots structure 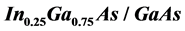 slow light devices based on exitonic cpo.
slow light devices based on exitonic cpo.
Keywords:
Slow Light, Coherent Population Oscillation, Quantum Dots, 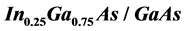 , Slow down Factor
, Slow down Factor

1. Introduction
Slow light attracted significant attentions to itself as a method to control significantly light velocity [1]. If the wave is mono color or mono-frequency, then the wave will release with phase speed in the environment, but if the wave isn’t mono-frequency, then the wave will be released with group velocity, which is calculated from the following equation: [2]
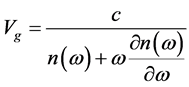 (1)
(1)
Where, 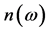 is refractive index and ω is frequency and c is the light speed in the vacuum. The vigorous changes in refractive index compared with frequency are used to decrease the light velocity or achieve slow light. The vigorous changes in refractive index compared to frequency occur in resonance frequency. So we conclude that the light pulse has the lowest group velocity in resonance frequency [2]. Several methods are used for decreasing the light velocity. These methods include Electromagnetically Induced Transparency (EIT), Coherent population Oscillation (CPO), Stimulated Brillouin scattering (SBS) and Stimulated Raman scattering (SRS) [3] [4] [8]. A significant reduction in the light velocity is achieved by using EIT in low temperature [5]. Despite the prominent growth in slowdown factor (SDF), EIT method requires a longer temporal coherence time, while CPO not only requires long resting time but also its execution is easier than EIT [1] [6]. Recently light velocity control in semiconductor devices which has solid shape has attracted more attention due to their potential use in photonic devices such as all-optical memories and quantum information processors [1] [9]. Slow light has been tested successfully in quantum wells and dots in low temperature by using cpo [1] [6]. semiconductor slow light devices with quantum well or dot structure control light velocity by using the life time of exciton and they decrease significantly group velocity by creating a steep slope in refractive index diagram. It should be noted that CPO with quantum well structure is similar to CPO with quantum dot structure, the difference is that exciton is Trapped in a 3-D cell. In fact, the 3-D cell increases the probability of execution of operation in room temperature. In this paper we simulate a slow light quantum dots device
is refractive index and ω is frequency and c is the light speed in the vacuum. The vigorous changes in refractive index compared with frequency are used to decrease the light velocity or achieve slow light. The vigorous changes in refractive index compared to frequency occur in resonance frequency. So we conclude that the light pulse has the lowest group velocity in resonance frequency [2]. Several methods are used for decreasing the light velocity. These methods include Electromagnetically Induced Transparency (EIT), Coherent population Oscillation (CPO), Stimulated Brillouin scattering (SBS) and Stimulated Raman scattering (SRS) [3] [4] [8]. A significant reduction in the light velocity is achieved by using EIT in low temperature [5]. Despite the prominent growth in slowdown factor (SDF), EIT method requires a longer temporal coherence time, while CPO not only requires long resting time but also its execution is easier than EIT [1] [6]. Recently light velocity control in semiconductor devices which has solid shape has attracted more attention due to their potential use in photonic devices such as all-optical memories and quantum information processors [1] [9]. Slow light has been tested successfully in quantum wells and dots in low temperature by using cpo [1] [6]. semiconductor slow light devices with quantum well or dot structure control light velocity by using the life time of exciton and they decrease significantly group velocity by creating a steep slope in refractive index diagram. It should be noted that CPO with quantum well structure is similar to CPO with quantum dot structure, the difference is that exciton is Trapped in a 3-D cell. In fact, the 3-D cell increases the probability of execution of operation in room temperature. In this paper we simulate a slow light quantum dots device 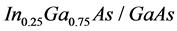 based on cpo and examine the effects of radius and height on the device’s parameters. The results of the paper are usable for all quantum dot devices based on cpo.
based on cpo and examine the effects of radius and height on the device’s parameters. The results of the paper are usable for all quantum dot devices based on cpo.
2. Theory
In Figure 1(a) slow light device is seen in which quantum dots are places on a layer in a uniform and similar way, also in Figure 1(b) a cylindrical geometrical shape is assumed for a quantum dot in which radius is denoted with r and height is denoted with h.
The CPO based slow light devices is a system which has two energy levels. In a 2-energy levels system, if the difference between signal and detuning frequency is in the range of inverse of carriers life, then it will have a significant CPO, because the life time of carriers is a temporal interval in which population oscillation is able to track the interference frequency induced by pump and signal [1]. The population oscillation can create a hole in the system’s absorption diagram which leads to intense changes in the real part of refractive index diagram and eventually leads to severe decrease of group velocity. For the semiconductor devices with quantum dot structure which are studied in this paper, we can use dynamic equations of density matrix to analyze the system comprehensive details for the analysis is available in reference [6]. The device’s Permeability Tensor is shown with 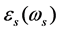 which a function of frequency and after solving the mentioned dynamic equation, it is defined as follows:
which a function of frequency and after solving the mentioned dynamic equation, it is defined as follows:
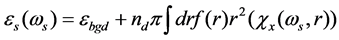 (2)
(2)
In above equation, 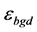 is background relative permeability and
is background relative permeability and 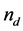 is the dots density per area unit and f(r) is the dots Gaussian distribution and
is the dots density per area unit and f(r) is the dots Gaussian distribution and  is signal frequency. The equation of refractive index
is signal frequency. The equation of refractive index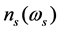 , absorption
, absorption

Figure 1. (a) The pump-probe scheme of population oscillation in QDs; (b) The geometry of a QD. The QD is modeled as a cylinder with height h and radius r.
coefficient 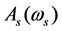 and slow down factor
and slow down factor 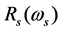 are as follows:
are as follows:
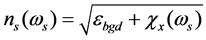 (3)
(3)


We consider the quantum dot system with 



3. Effects of Changes in Quantum Dot’s Radius
Figure 3 shows the diagram of real part of the refractive index for semiconductor slow light device with the mentioned structure with three different radius 6, 8 and 10 nm for quantum dots in the light device. In this part, the real part of refractive index for a radius of 6 is simulated. It can be noticed that the real part of the refractive index of the quantum dots with a radius of 6 nm has a sharper slope compared with quantum dots with a radius of 8 and 10 nm, so we expect that it has a larger SDF and it further reduces the group velocity.


Figure 2. (a) Absorbance, (b) Real part of refractive index, and (c) Slow down factor plotted as functions of detuning between signal and pump, due to excitonic population oscillation in InGaAs/GaAs quantum dots described in [6].
Figure 3. Variations of real part of refractive index of slow light device with three different radius of quantum dots as a function of detuning.
The 3 dimensional diagrams of real part of refractive index and SDF is drawn for simultaneous changes of radius and detuning to achieve a better understanding of the subject (Figure 4).
In Figure 4(a) the diagram of real part of refractive index is drawn in terms of radius changes and the changes of frequency. If we look at the curve along the detuning, then we will find that the greatest slope of diagram is related to detuning equal to zero. Now, if we look at the curve along the height changes, then we will find that the curves’ slope increases as the radius decreases. It means that if the radius increases in constant detuning then the curve’s slope will decrease. Figure 4(b) shows the SDF in terms of the simultaneous changes of detuning and radius. First, along the change of detuning maximum SDF is related to the detuning of zero and if we study the diagram along the radius changes then we will find that SDF decreases when radius increases. Due to the dependence of exciton energy to the dimensions of the quantum dots, the changes in radius of quantum dots will definitely leads to the change of exciton energy and eventually it causes changes in frequency in the above diagrams, but we just examined the effects of changes in dimensions of the quantum dots on the SDF and group velocity, therefore, the effects of the dimension change on the frequency and exciton energy are ignored [7] [8].
4. Effects of Change in the Height
Figure 5 shows the diagram of real part of the refractive index for semiconductor slow light device with the mentioned structure with three different heights. In this figure, the real part of refractive index is simulated and drawn for heights of 3, 5 and 7 nm for quantum dots in the light device. As can be seen in the figure, the diagram of quantum dots with height of 3 nm has a sharper slope than heights of 5 and 7 nm, so they are expected to have a greater SDF, meaning that they decrease group velocity greatly. For better understanding the subject, 3-D diagrams of real part of refractive index and SDF are drawn for simultaneous changes of height and detuning according to Figure 6.
If we consider the strike of detuning in Figure 6(a) which shows real part of refractive index in terms of simultaneous changes of detuning and height, then we will find that the greatest slope occur when difference is equal zero, if we move along the height changes axis, then we will find that as height increases the curve’s slope decreases.
If we look at Figure 6(b) along detuning which shows the diagram of SDF in terms of simultaneous changes of detuning and height, then we will find that the maximum value of the curve occurs in detuning of zero and if we check it along the height changes axis, then we will find that height has a reverse equation with slow down factor. As mentioned in Section 3, with respect to the dependence of exciton energy to the dimension of quantum dot, the changes in height of quantum dots will certainly lead to changes in exciton energy and finally lead to frequency changes in the above curves, since we just examine the effects of changes of quantum dot dimension on the SDF and group velocity, the effects of the dimension change on the frequency and exciton energy are ignored [7] [8].
5. Result and Discussions
This paper studies and simulates a sample of semiconductor slow light devices with quantum dot structure and

Figure 4. Variations of the (a) Real part of refractive index; (b) Slow down factoras function of radius and detuning.
Figure 5. Variations of real part of refractive index of slow light device with three different height of quantum dots as a function of detuning.

Figure 6. Variations of the (a) real part of refractive index; (b) slow down factor as function of height and detuning.
we suggested new techniques for setting output specifications of these devices. Based on the obtained results, it can be said when the size of quantum dot is decreased, the slope of real part of refractive index curve increases and therefore, a bigger SDF is achieved. In this paper the maximum SDF for radius is equal to 3 nm and the height equal to 2 nm which is achieved is equal 4560 which is eighteen times larger than the reference paper [6]. Of course, the radius decrease causes frequency shift too.
Cite this paper
Bahram Choupanzadeh,Hassan Kaatuzian,Reza Kohandani,Saeed Abdolhosseini, (2016) Simulation and Characteristics Improvement of Quantum Dot Slow Light Devices by Geometrical Dimension Alteration. Optics and Photonics Journal,06,114-119. doi: 10.4236/opj.2016.68B019
References
- 1. Chang, S.W., Chuang, S.L., Ku, P.C., Chang-Hasnian, C.J., Palinginis, P. and Wang, H. (2004) Slow Light Using Excitonic Popula-tion Oscillation. Phys Rev. B, 70, 235333. http://dx.doi.org/10.1103/PhysRevB.70.235333
- 2. authier, D., Gaeta, A.L. and Boyd, R.W. (2006) Slow Light: From Basics to Future Prospects. Photonicsspectra, 44-50.
- 3. Kaatuzian, H. (2009) Photonics. 2nd Edition, Vol. 2, AKU Press, in Persian.
- 4. Bigelow, M.S., Lepeshkin, N.N. and Boyd, R.W. (2003) Superluminal and Slow Light Propagation in a Room-Tem- perature Solid. Science, 301, 200-202. http://dx.doi.org/10.1126/science.1084429
- 5. Hau, L.V., Harris, S.E., Dutton, Z. and Behroozi, C.H. (1999) Light Speed Reduction to 17 Meters per Second in an Ultracold Atomic Gas. Nature, 397, 594-598. http://dx.doi.org/10.1038/17561
- 6. Chang, S.-W. and Chuang, S.L. (2005) Slow Light Based on Population Oscillation in Quantum Dots with Inhomogeneous Broadening. Phys. Rev. B, 72, 235330.
- 7. Kohandani, R., Zandi, A. and Kaatuzian, H. (2014) Analysis of the Effects of Applying External Fields and Device Dimensions Alterations on GaAs/AlGaAs Multiple Quantum Well Slow Light Devices Based on Excitonic Population Oscillation. Applied Optics, 53, 1228-1236. http://dx.doi.org/10.1364/AO.53.001228
- 8. Kaatuzian, H., Kojori, H.S., Zandi, A. and Ataei, M. (2013) Analysis of Quantum Well Size Alteration Effects on Slow Light Device Based on Excitonic Population Oscillation. Optical and Quantum Electronics, 45, 947-959. http://dx.doi.org/10.1007/s11082-013-9703-3
- 9. Ma, S.M., Xu, H. and Ham, B.S. (2009) Optical Society of America, Electro-magnetically Induced Transparency and Slow Light in GaAs/AlGaAs Multiple Quantum Wells in Atransient Regime. 17.






