Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70302,9 pages
10.4236/opj.2016.68B010
Simulation of Chirped Pulse Propagation in Silicon Nanowires: Shape and Spectrum Analysis
Hassan Pakarzadeh1, Zeinab Delirian1, Mostafa Taghizadeh2
1Department of Physics, Shiraz University of Technology, Shiraz, Iran
2Atomic and Molecular Group, Faculty of Physics, Yazd University, Yazd, Iran



Received 6 May 2016; accepted 20 August 2016; published 25 August 2016

ABSTRACT
In this paper, we simulate the propagation of chirped pulses in silicon nanowires by solving the nonlinear Schrödinger equation (NLSE) using the split-step Fourier (SSF) method. The simulations are performed both for the pulse shape (time domain) and for the pulse spectrum (frequency domain), and various linear and nonlinear effects changing the shape and the spectrum of the pulse are analyzed. Owing to the high nonlinear coefficient and a very small effective-mode area, the required length for observing nonlinear effects in nanowires is much shorter than that of conventional optical fibers. The impacts of loss, nonlinear effects, second- and third-order dispersion coefficients and the chirp parameter on pulse propagation along the nanowire are investigated. The results show that the sign and the value of the chirp parameter have important role in pulse propagation so that in the anomalous dispersion regime, the compression occurs for the up- chirped pulses, whereas the broadening takes place for the down-chirped pulses. The opposite situation happens for up- and down-chirped pulses propagating in the normal dispersion regime.
Keywords:
Silicon Nanowire, Nonlinear Schrödinger Equation, Chirp, Pulse Propagation

1. Introduction
Low cost, availability as well as linear and nonlinear optical properties of silicon has caused silicon to be an ideal material for the production of nanoscale integrated photonic devices [1]-[6]. Large refractive index of silicon (n = 3.5) compared to the small refractive index of cladding (n = 1 for air and n = 1.45 for silica) leads to tight light confinement [1] [3]-[7]. Such strong light confinement, allows the waveguide silicon devices to have a very small cross-section in the order of nanometer and such devices are called silicon nanowires. Reduction of the nanoscale cross-section together with the high refractive-index contrast would lead to two distinct advantages: First, the ability to control the dispersion and high optical field intensity; Second, potential applications of silicon for nonlinear optics [1] [5] [6] [8]. Although silicon does not exhibit second-order nonlinear effects, it possesses a very high nonlinear optical third-order susceptibility, approximately 3 to 4 times larger than that of the silica [1] [5] [6]. In silicon, these large third-order nonlinear effects associated with strong light confinement leads to a further increase of optical nonlinear effects. This increase itself results in reducing the required input power for observing strong nonlinear effects and also a reduced length for optical devices with several hundred micrometers to millimeters [9] [10].
There are two types of chirped pulses: up-chirp in which the frequency increases with time and down-chirp where the frequency decreases with time. In some sources, chirp is synonymous with swept signal and is used in SONAR, RADAR, communications and high pulse energy amplifiers [11] [12]. Ultra-short laser pulses also exhibit chirp and cause an increase or a decrease of dispersion in optical transmission systems during signal propagation, which is dependent on the sign of the input chirp [13]. Large dispersion and high third-order nonlinear coefficient of silicon (Si) photonic nanowires lead to high interplay between the linear and the nonlinear physics in these waveguides. For the fem to second pulses, it is necessary to include the third-order dispersion coefficient (TOD), β3, in the theory to investigate the pulse propagation in the nanowire [14].
In this paper, the evolution of chirped pulses along the silicon nanowires is simulated and impacts of second- and third-order dispersion coefficients and also loss on pulse evolution are investigated. Moreover, a comparison is made between different cases of chirped and non-chirped input pulses.
2. Theory and Simulation Results
In this section, theoretical framework as well as the numerical method for investigation of fem to second chirped pulse propagation in silicon nanowires are presented. The governing equation is the nonlinear Schrödinger equation (NLSE) which is defined as [15]:
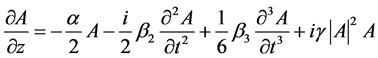 (1)
(1)
where A represents the envelope of the pulse, α is the loss of nanowire and γ denotes The nonlinear parameter. Also, β2 and β3 are the second- and the third-order dispersion coefficients of the nanowire calculated at the pulse wavelength, respectively. Different terms on the right-hand side of Equation (1) are respectively responsible for the attenuation, group-velocity dispersion (GVD), third-order dispersion (TOD) and self-phase modulation (SPM). Basically, the linear effects (including the loss, GVD and TOD) are responsible for changes in pulse shape while nonlinear effects (such as SPM) are responsible for changes of pulse spectrum. As it will be seen, the interplay of linear and nonlinear effects leads to both the temporal and spectral changes of the pulse.
The well-known method for numerically solving the NLSE is the split-step Fourier method (SSFM). We implement a code in MATLAB based on SSFM for different cases of chirped and non-chirped and also the presence or absence of loss and second- and third-order dispersion coefficients. We input a Gaussian pulse with a center wavelength of 1527 nm, a pulse width of 204 fs and a peak power of 40 mW into a single mode nanowire of Si with a cross-section of 445 × 220 nm2 and a length of 4.7 mm [9], and investigate the impact of different factors during the pulse propagation. Input Gaussian pulse equation is described as:
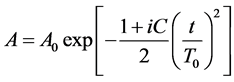 (2)
(2)
where A0 is maximum amplitude and C is the chirp parameter. T0 shows half pulse width at 1/e of peak intensity. At first, we start with a simple case where only nonlinear effects (SPM) with second-order dispersion (GVD) are considered in NLSE. We consider γ = 2.2 × 104 (W∙m)−1 and β2 = −3.89 ps2/m, and as is seen from Figure 1(a), the impacts of GVD and SPM are to deform (to broaden) the pulse shape, symmetrically. Here third-order dispersion, chirp and loss of nanowire are not included. As the pulse propagates along the nanowire, the dispersion causes the pulse broadening and gradually by influencing the nonlinear effect, the pulse shape deviates from the Gaussian one, and hence sidebands around the central peak at the length of ~3 mm are observed. Figure 1(b) shows the input and output pulse shape and spectrum at the input and output of the nanowire, respectively. As it can be seen both the output pulse shape and spectrum are different from those of input ones, owing to the combined effects of GVD and SPM.
By adding the loss of 3.5 dB/cm, we see that the power level reduces by a factor of ~2 (Figure 2(a)). The effective length decreases according to Equation (3) and as a result, the sidebands are observed at larger length (~4 mm) than in Figure 1(a). This means that the pulse should propagate longer length to see the considerable SPM


Figure 1. (a) Pulse evolution along the nanowire in the presence of GVD and SPM effects and (b) input and output pulse shapes (left column) and pulse spectra (right column). Here, loss, TOD and chirp are not included.


Figure 2. (a) Pulse evolution along the nanowire and (b) input and output pulse shapes (left column) and pulse spectra (right column). Here, the loss is included whereas the input chirp is still zero and other parameters are the same as those in Figure 1.
and nonlinear phase shift. In Figure 1(b) the input and output pulse shape (left column) and pulse spectrum (right column) are shown where the deviation from the input Gaussian form is very evident. Particularly, the output spectrum is very different from the input spectrum due to the nonlinear phase shift acquired by the pulse during the propagation.
Now, if we make our model more realistic and consider the input chirp parameter, it can be seen from Figure 3(a) that the up-chirped pulse with C = +5 in the anomalous dispersion regime (where β2C > 0) is compressed at ~2 mm and then converted to a top-hat pulse. In contrast, for a down-chirped pulse with C = −5, β2C is positive and the pulse is broadened without any compression (Figure 3(b)). Therefore, the sign of the chirp parameter is very important in pulse propagation properties along the nanowire. As seen in both Figure 3(a) and Figure 3(b), the pulse is still symmetrical, because the TOD is zero. Again, the input and the output pulse shape (left column) and pulse spectrum (right column) can be seen for each case of C = +5 or C = −5, in Figure 3(c) and Figure 3(d), respectively. Significant changes can be seen if each plot of Figure 3 is compared to the corresponding plot of Figure 2. This reveals the critical role of the input chirp parameter on the propagation characteristic of ultra-short pulses in Si nanowires.
Finally, if we complete the model and include the third-order dispersion coefficient β3 = −0.435 ps3/m in NLSE, it is seen that asymmetric variations in pulse shape and pulse spectrum occur which are totally different in comparison with those in Figure 3. These variations are shown in Figure 4(a) and Figure 4(b). Since the sign of β3 is negative, the variations or oscillations appear on the leading edge of the pulse. The opposite situation is expected for the case when is β3 positive. The output shape and spectrum are completely deviated from the Gaussian and again since β2C > 0, the pulse compression happens ~1mm. Moreover, since the pulse is initially up-chirped, the additional nonlinear chip is acquired during the pulse propagation along the nanowire and hence new frequency components are added to the pulse spectrum. That is why a new peak is appeared in Figure 4(b) at the output spectrum. This means that the initial chirp together with TOD have significant role in shape and spectrum evolutions of ultra-short pulses.
To see the important roles of the initial chirp(C) and the TOD (β3) more explicitly, we plot the output pulse shape and the output pulse spectrum for two different cases: with and without chirp and TOD. This is shown in Figure 5, where the impacts of the initial value of the input chirp on the output pulse shape and pulse spectrum are plotted for the case of β3 = 0 (Figure 5(a) and Figure 5(c)) and β3 = −0.435 ps3/m (Figure 5(b) and Figure 5(d)), respectively. Here, an up-chirped pulse with C > 0 is assumed and all effects including the nanowire loss,




Figure 3. Pulse evolution along the nanowire by including the input chirp parameter of (a) C = +5 and (b) C = −5. Input and output pulse shapes (left columns) and pulse spectra (right columns) are seen for (c) C = +5 and (d) C = −5, respectively. Other parameters are the same as those in Figure 2.


Figure 4. Pulse evolution along the nanowire for (a) the up-chirped pulse with C = +5 when TOD is included together with (b) the input and output pulse shapes (left column) and pulse spectra (right column).




Figure 5. Output pulse shapes (a) without and (b) with inclusion of TOD for various input chirp parameters; together with (c) and (d) corresponding pulse spectra. Here, loss, GVD and SPM are considered for all plots.
GVD and SPM are taken into account. As it is apparent, for both cases, by increasing the initial chirp value, the pulse shape and the spectrum are dramatically broadened. As expected, the symmetry in the pulse shape and the pulse spectrum is preserved in Figure 5(a) and Figure 5(c) which is due to the absence of TOD. This is while in Figure 5(b) and Figure 5(d), owing to the presence of TOD, the symmetry is broken and some variations or oscillations appear on the left part of the plots which is because of the negative sign of TOD. In fact in all cases, the up-chirped pulse with C = 7 experiences more broadening and variations in both time and frequency domain.
3. Conclusion
Silicon nanowires have great potential for exhibiting the nonlinear effects and they are good candidates for applications in very small-scale photonic components. We have shown that when an ultra-short pulse propagates along the Si nanowire, GVD causes symmetric temporal broadening, while TOD changes the pulse shape asymmetrically. The loss decreases the effective length and lowers the power level without a significant change in overall behavior of the pulse shape and spectrum. In particular, the input chirp parameter has a significant role on the evolution of the pulse shape and spectrum along the nanowire. For the up-chirped pulses in the anomalous dispersion regime, where β2C is negative, pulse compression occurs and vice versa. In addition, by increasing the value of the input chirp, changes in both the pulse shape and the pulse spectrum are dramatically increased. The results of this research can be used for pulse shaping and signal processing in silicon nanowires.
Acknowledgements
The authors would like to thank Dr. Michael Frosz for his assistance with numerical code of NLSE.
Cite this paper
Hassan Pakarzadeh,Zeinab Delirian,Mostafa Taghizadeh, (2016) Simulation of Chirped Pulse Propagation in Silicon Nanowires: Shape and Spectrum Analysis. Optics and Photonics Journal,06,53-61. doi: 10.4236/opj.2016.68B010
References
- 1. Koos, C., Jacome, L., Poulton, C., Leuthold, J. and Freude, W. (2007) Nonlinear Silicon-on Insulator Waveguides for All-Optical Signal Processing. Opt. Express, 15, 5976-5990. http://dx.doi.org/10.1364/OE.15.005976
- 2. Tong, L.M., Gattass, R.R., Ashcom, J.B., He, S.L., Lou, J.Y., Shen, M.Y., Maxwell, I. and Mazur, E. (2003) Subwavelength-Diameter Silica Wires for Low-Loss Optical Wave Guiding. Nature, 426, 816-819. http://dx.doi.org/10.1038/nature02193
- 3. Tong, L., Lou, J. and Mazur, E. (2004) Single-Mode Guiding Properties of Subwavelength Diameter Silica and Silicon Wire Waveguides. Opt. Express, 12, 1025-1035. http://dx.doi.org/10.1364/OPEX.12.001025
- 4. Dulkeith, E., Xia, F., Schares, L., Green, W.M.J. and Vlasov, Y.A. (2006) Group Index and Group Velocity Dispersion in Silicon-on-Insulator Photonic Wires. Opt. Express., 14, 3853-3863. http://dx.doi.org/10.1364/OE.14.003853
- 5. Foster, M., Turner, A., Lipson, M. and Gaeta, A. (2008) Nonlinear Optics in Photonic Nanowires. Opt. Express, 16, 1300-1320. http://dx.doi.org/10.1364/OE.16.001300
- 6. Driscoll, J.B., Osgood, R.M., Grote, R.R., Dadap, J.I. and Panoiu, N.C. (2015) Squeezing Light in Wires: Fundamental Optical Properties of Si Nanowire Waveguides. J. Lightwave Technol., 33, 3116-3131. http://dx.doi.org/10.1109/JLT.2015.2431984
- 7. Lin, Q., Painter, O.J. and Agrawal, G.P. (2007) Nonlinear Optical Phenomena in Silicon Waveguides: Modeling and Applications. Opt. Express, 15, 16604-16644. http://dx.doi.org/10.1364/OE.15.016604
- 8. Schmidt, V., Wittemann, J.V., Senz, S. and G?sele, U. (2009) Silicon Nanowires: A Review on Aspects of their Growth and Their Electrical Properties. Adv. Mater., 21, 2681-2702. http://dx.doi.org/10.1002/adma.200803754�
- 9. Hsieh, I., Chen, X., Dadap, J.I., Panoiu, N.C. and Osgood, R.M. (2007) Cross-Phase Modulation-Induced Spectral and Temporal Effects on Co-Propagating Femtosecond Pulses in Silicon Photonic Wires. Optics Express, 15, 1135-1146 http://dx.doi.org/10.1364/OE.15.001135.
- 10. Lavdas, S., Driscoll, J.B., Grote, R.R., Osgood, R.M. and Panoiu, N.C. (2013) Gen-eration and Collision of Optical Similaritons in Dispersion-Engineered Silicon Photonic Nanowires. SPIE, 8816, 88160J-88169J.
- 11. Delfyett, J., Mandridis, D., Piracha, M., Nguyen, D., Kim, K. and Lee, S. (2012) Chirped Pulse Laser Sources and Applications. Progress in Quantum Electronics, 36, 475-540. http://dx.doi.org/10.1016/j.pquantelec.2012.10.001
- 12. Piracha, M.U., Nguyen, D., Ozdur, I. and Delfyett, P.J. (2011). Simultaneous Ranging and Velocimetry of Fast Moving Targets Using Oppo-sitely Chirped Pulses from a Mode-Locked Laser. Optics Express, 19, 11213-11219. http://dx.doi.org/10.1364/OE.19.011213
- 13. Cao, Y., Zhang, L., Fei, Y., Lei, X. and Chen, S. (2015) Effect of Frequency Chirp on Super Continuum Generation in Silicon Waveguides with Two Zero-Dispersion Wavelengths. Opt. Commun., 334, 190-195. http://dx.doi.org/10.1016/j.optcom.2014.08.043
- 14. Osgood, R.M., Panoiu, N.C., Dadap, J.I., Liu, X., Chen, X., Hsieh, I-W., Dul-keith, E., Green, W.M.J. and Vlasov, Y.A. (2009) Engineering Nonlinearities in Nanoscale Optical Systems: Physics and Applications in Dispersion-Engineered Silicon Nanophotonic Wires. Adv. Opt. Photon., 1, 162-235. http://dx.doi.org/10.1364/AOP.1.000162
- 15. Agrawal, G.P. (2006) Nonlinear Fiber Optics. 4th Edition, Academic Press.

