Optics and Photonics Journal
Vol.06 No.08(2016), Article ID:70296,7 pages
10.4236/opj.2016.68B006
Evaluation of the Coherent Combining Lasers Array by the Power in the Bucket of the Main Lobe Method
Yang Liu, Xi Zhang, Debao Zhang, Wenqin Huang, Chang’an Qiao, Bo Wang
Wuhan Mechanical Technology College, Wuhan, China



Received 25 April 2016; accepted 19 August 2016; published 25 August 2016

ABSTRACT
Coherent combination of laser beam is an important and challenging area of high power laser science. And how to evaluate the high power laser by coherent beam combination is a new research spot. Formulas for the radiated intensity distributions of coherent combined Gaussian beam array are derived via Fraunhofer scalar diffraction model by utilizing representations of the cross-spectral density of the far field. Effects of beam array numbers and separate distances etc. on far field radiated profiles are shown and analyzed. A new conception named power in the bucket of the main lobe (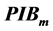 ) is advanced to measure the beam quality of combined beams. This evaluation method is useful for efficiently determining the peak irradiance and power in the bucket for single emitting apertures of general shape.
) is advanced to measure the beam quality of combined beams. This evaluation method is useful for efficiently determining the peak irradiance and power in the bucket for single emitting apertures of general shape.
Keywords:
Coherent Combination, Beam Shape, Fill Factor, Power in the Bucket

1. Introduction
Achieving high optical power and high brightness has always been the major goals in the development of laser technologies. A natural means of increasing the power and especially the brightness should be to combine many individual lasers into arrays. In recent years, coherent and incoherent combinations of laser beams have been intensively studied theoretically and experimentally due to their wide applications in long-range energy delivering, etc. Since then, beam quality and divergence angle of laser arrays in the far field have also been investigated, and how to evaluate the high power laser by coherent beam combination is a new research hotspot [1] [2].
In this paper, based on the representations of the cross-spectral density of the far field, the radiated intensity distributions of coherent and incoherent combined Gaussian laser arrays are formulated and depicted. Effects of beam array numbers and separate distances between each source element on far-field radiated profiles are illustrated by numerical examples.
The important motivation for combining multiple lasers is to obtain high on-axis peak beam intensity, so the combination effect is evaluated by combining effect factor defined as the power in the bucket of the main lobe (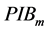 ) at the far field target. The
) at the far field target. The 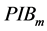 is defined as
is defined as
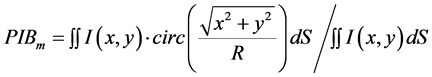 (1)
(1)
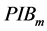 is the ratio of the power in the main lobe to the total power of the array in the far filed intensity distribution. On this basis, a new conception is advanced to measure the beam quality of combined beams.
is the ratio of the power in the main lobe to the total power of the array in the far filed intensity distribution. On this basis, a new conception is advanced to measure the beam quality of combined beams.
2. Theory Model
According to Fraunhofer diffraction theory, the diffraction field that collimated beam passing through lens can be calculated by Fraunhofer diffraction formula. In this paper, we established a laser combination array of several individual Gaussian beams with a near-field intensity profile arranged of a hexagonally packed group of emitters on a circle in a “bolt-hole” beam pattern as shown in Figure 1, and the far field beam profile calculation is based on scalar diffraction theory. The far field complex amplitude distribution is sensitive to near field beam relative phase relationship; array areal fill factor and array number [3]-[5]. We assume that every beam in the array has same intensity distribution with different beam center positions, and every beam waist width is equal
as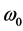 , the distance between nearest beams is d, the total number of the laser array is N,
, the distance between nearest beams is d, the total number of the laser array is N, ,m is the circle number of the array.
,m is the circle number of the array.
The coordinate location of each beam can be referred as (xmn, ymn),
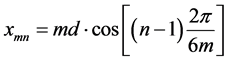 ,
,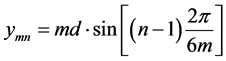 (2)
(2)
The intensity of the laser array in the near field pattern can be written as
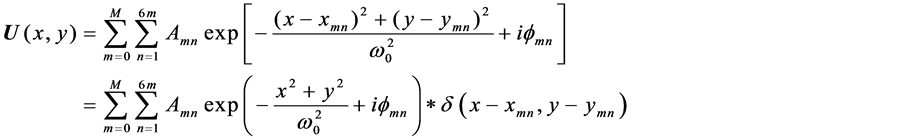 (3)
(3)
where, 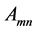 ,
,  is the complex amplitude and initial phase of each beam respectively. The far field profile is the spatial Fourier transform of the near field pattern, and the far field complex amplitude of coherent combined Gaussian laser array can be expressed as
is the complex amplitude and initial phase of each beam respectively. The far field profile is the spatial Fourier transform of the near field pattern, and the far field complex amplitude of coherent combined Gaussian laser array can be expressed as
 (4)
(4)
Figure 1. Arrangement of array beams.
The far field cross-spectral intensity distribution pattern is the square of the complex amplitude model. For simplicity, we neglected the constant items, and the far field intensity distribution pattern of the array is easy to get as
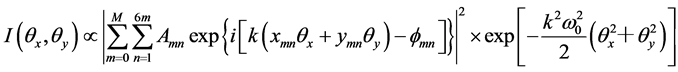 (5)
(5)
where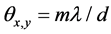 ,and we will see that the far field cross-spectral intensity distribution pattern is the product of the intensity of the laser array in the near field pattern with a single Gaussian beam. We induce a spatial coherence degree factor
,and we will see that the far field cross-spectral intensity distribution pattern is the product of the intensity of the laser array in the near field pattern with a single Gaussian beam. We induce a spatial coherence degree factor 




3. The Far Filed Characters upon Sensitive Factors
According to Fraunhofer diffraction theory, the diffraction field that collimated beam passing through lens can be calculated by Formula (5), where i is imaginary unit, k is wave number 

3.1. The Array Arrangement
In this section, we study the performance of the array arrangement to the far field distribution. Suppose that there are only static phase distortions due to the laser path length differences between the different channels. Numerical calculations will be carried out to correct those phase distortions by finite number of iterations. We will consider hexagonal distributed laser arrays containing seven lasers as an example. We suppose that each fiber laser beam has a single Gaussian mode output. The beam waist of each laser is


From results it is found that, for coherent combination of Gaussian laser array, its intensity distributions would turn out to be occupy many rough lobes around the a central lobe. For example, when
3.2. The Coherence Degree
We induce a spatial coherence degree factor 



The computed results indicate that the radius of the main lobe of the far field distribution is consistent despite the variation of coherence degree factor
Figure 2. Far field distribution with various f: (a) f = 1.0 (b) f = 0.8 (c) f = 0.5 (d) f = 0.25.
Figure 3. Far field distribution with various γ.
may be the most important character is that, the fringe visibility at the far field does depend on the coherence degree but that dependence varies strongly with the array arrangement and the number of laser beams in the array.
3.3. The Number of Array Beams
The equations are an exception to the prescribed specifications of this template. You will need to determine whether or not your equation should be typed using either the Times New Roman or the Symbol font (please no other font). Equations should be edited by Mathtype, not in text or graphic versions. You are suggested to use Mathtype 6.0 (or above version).
From the Formula (5) of the theory model, total number of wavelets of the combination array does some effect to the far field intensity [7]. In this section, we computed the power of the main lobe versus the variable number of beams at a certain value of f. Figure 4 shows the calculated 
In the graph, m is the circle number of the array arrangement and the total number of the array is
that, the effect to the 



4. Power in the Bucket of the Main Lobe
In this section we discuss the way how to rough evaluate the coherent beam combination by the method of power in the main lobe of the array’s far field distribution. From the above analysis in Section 2 and Section 3, we know that for a given laser array, its far filed intensity distribution is determined by the factors of

Figure 4. PIBm versus various m at certain f.
Figure 5. Near and far filed distribution and the PIBm value when m = 1, 3, 5.
By the Formulas (4) and (5), we can calculate the 

5. Conclusion
In this paper, we have presented formulas for the radiated intensity distributions of coherent combined Gaussian beam array via Fraunhofer scalar diffraction model. We then deduced a set of formulae useful for efficiently determining the peak irradiance and power in the bucket for single emitting apertures of hexagonal distributed laser arrays. The far-field intensity distribution for coherent combination is numerically calculated and the sensitive factors are discussed in detail. A new conception named power in the bucket of the main lobe (

Cite this paper
Yang Liu,Xi Zhang,Debao Zhang,Wenqin Huang,Chang’an Qiao,Bo Wang, (2016) Evaluation of the Coherent Combining Lasers Array by the Power in the Bucket of the Main Lobe Method. Optics and Photonics Journal,06,30-36. doi: 10.4236/opj.2016.68B006
References
- 1. Fan, T.Y. (2005) Laser Beam Combining for High-Power High Radiance Sources. IEEE J. Quantum. Electron., 11, 567-577. http://dx.doi.org/10.1109/JSTQE.2005.850241
- 2. Li, Y.Z., Qian, L.J., Lu, D.Q., Fan, D.Y., Wen, S.C. (2007) Coherent and Inco-herent Combining of Fiber Array with Hexagonal Ring Distribution. Opt Laser Tech, 39, 957-63. http://dx.doi.org/10.1016/j.optlastec.2006.06.010
- 3. Zhou, Y., Liu, L.P., Peng, Q.J., et al. (2005) Phase Locking of Laser Array. SPIE, 6028, 602803.
- 4. Evans, G.A. and Hammer, J.M. (1993) Surface Emitting Semiconductor Lasers And Arrays. Academic Press, New York.
- 5. Nabors, C.D. (1994) Effects of Phase Errors on Coherent Emitter Arrays. Appl Opt, 33, 2284-2289. http://dx.doi.org/10.1364/AO.33.002284
- 6. Renwick, S.P. (2005) What Makes a Coherence Curve Change? Proc. of SPIE, 5754, 1537-1547. http://dx.doi.org/10.1117/12.598939
- 7. Li, J., Chen, Y.R., Xu, S.X., et al. (2009) Far-Field Radiation of Coherent and Incoherent Combined Lorentz-Gaussian Laser Array. Proc. of SPIE, 7749, 1-6
- 8. Smith, I.W. (2011) Beam Shape of Coherently-Combined Optical Arrays. Proc. of SPIE, 8052, 1-15. http://dx.doi.org/10.1117/12.883402
- 9. Tan, Y. and Li, X.Y. (2012) Numerical Analysis of Beam Quality Factor β on Coherent. Proc. of SPIE, 8551, 85511-1-9.






