Int'l J. of Communications, Network and System Sciences
Vol.2 No.5(2009), Article ID:600,7 pages DOI:10.4236/ijcns.2009.25041
Regulation of Queue Length in Router Based on an Optimal Scheme
Key Laboratory of Integrated Automation of Process Industry, Northeastern University, Shenyang, China
Email: nannanathome@163.com
Received July 12, 2008; revised January 20, 2009; accepted March 5, 2009
Keywords: Congestion Control, Sliding Mode Control (SMC), Active Queue Management (AQM),Kelly’s Proportional Fair Scheme
ABSTRACT
Based on the proportionally fair scheme that Kelly proposed to solve the optimization problems for utility function in networks, and in order to improve the congestion control performance for the queue in router, the linear and terminal sliding active queue management (AQM) algorithms are designed. Especially in the terminal sliding AQM algorithm, a special nonlinear terminal sliding surface is designed in order to force queue length to reach the desired value in finite time. The upper bound of the time is also obtained. Simulation results demonstrate that the proposed congestion algorithm enables the system be better transient and stable performance. At the same time, the robustness is guaranteed.
1. Introduction
Active Queue Management (AQM), as a class of packet dropping/marking mechanism in the router queue, has been recently proposed in order to convey congestion notification early enough to the senders, so that the senders are able to reduce the transmission rates before the queue overflows and any sustained packet loss occurs [1]. There are three typical kinds of AQM algorithms: One is heuristic algorithms, such as RED (Random Early Detection) [2], BLUE [3]; One is the utility function optimal model based on economics, like REM (Random Exponential Marking) [4], AVQ (Adaptive Virtual Queue) [5]; The other one is based on the sourcing and queuing dynamic model, as PI [6] and VRC (Virtual Rate Control) [7]. The advantage of the latter two algorithms is that the design of controller is based on explicit model, so the stability analysis and parameters modulation can be given theoretically.
TCP/AQM dynamics have time varying roundtrip times (RTTs) and uncertainties, which requires more robustness for the designed schemes. This paper focus on the source algorithm which Kelly [8] proposed based on economic utility function through an optimization framework. It is well known that sliding mode control (SMC) is an effective method of robustness control, and sliding mode control systems possess strong robustness against parameter perturbations and external disturbances [9], which is very suitable for time varying network system. In the recent years, many studies have been focus on the domain [10-12]. In these papers, they proposed robust sliding mode control algorithms. Because the three controllers are insensitive to variance of the network parameters, they are suitable for time-varying network systems. However, one of the representative characteristics of the three controllers is that the convergence of the system states to the equilibrium point is asymptotical but not in finite time, which means the queue length in buffer, can not converge to the desired value in finite time. In addition, there still exists chattering when system motion is in steady state. Recently, the terminal sliding mode control (TSMC) has been developed [13, 14], which can guarantee the finite reaching time to the sliding surface from initial states and the finite reaching time to the equilibrium point.
Kelly et al. [8] have studied the convergence in the presence of communication delays [4,15] through an optimization framework, which is a new and effective method to analyze the performance of congestion control for the Internet. So in this paper we propose an AQM algorithm based on Kelly’s scheme by using sliding mode control. The structure of the paper are as follows: in Section 2 we analyze the Kelly’s method, in Section 3 and 4, we design the linear and terminal sliding mode AQM controller respectively to study the convergence of the queue, the conclusion is given in the last section.
2. Kelly’s Optimal Scheme
In this section we briefly describe the rate allocation problem in the Kelly’s optimization framework.
Consider a network with a set L of resources and a set I of users. Let  denote the finite capacity of resource
denote the finite capacity of resource . Each user
. Each user  has a fixed route
has a fixed route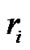 , which is a set of resources traversed by user i’s packets. We define a zero-one matrix A, where
, which is a set of resources traversed by user i’s packets. We define a zero-one matrix A, where 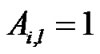 if
if  and
and  otherwise. When its rate is
otherwise. When its rate is , user i receives utility
, user i receives utility . We take the view that the utility functions of the users are used to select the desired rate allocation among the users. The utility
. We take the view that the utility functions of the users are used to select the desired rate allocation among the users. The utility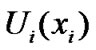 is an increasing, strictly concave and continuously differentiable function of
is an increasing, strictly concave and continuously differentiable function of 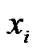 over the range
over the range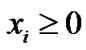 . Under this setting, the rate allocation problem of interest can be formulated as the following optimization problem [15]:
. Under this setting, the rate allocation problem of interest can be formulated as the following optimization problem [15]:
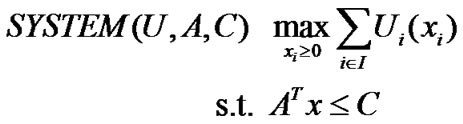 , (1)
, (1)
where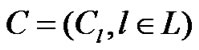 .The first constraint is the capacity constraint which states that the sum of the rates of all users utilizing resource should not exceed its capacity
.The first constraint is the capacity constraint which states that the sum of the rates of all users utilizing resource should not exceed its capacity .
.
Each user i adjusts its rate according to the following differential equation.
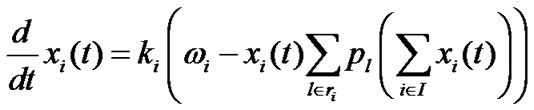 , (2)
, (2)
where![]() and
and  are positive constants,
are positive constants, ![]() is the gain parameter
is the gain parameter shows the users’ willingness to pay per unit time.
shows the users’ willingness to pay per unit time. 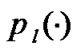 is an increasing function of the aggregate rate of the users going through it, and it can also be seen as the packet loss function that similar to ECN possibility function [16].
is an increasing function of the aggregate rate of the users going through it, and it can also be seen as the packet loss function that similar to ECN possibility function [16].
The simplified dynamic model is
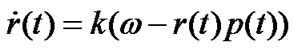 , (3)
, (3)
where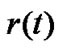 is the user’s sending rate at time t,
is the user’s sending rate at time t, 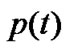 is the marker probability of ECN,
is the marker probability of ECN, 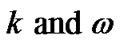 are the corresponding parameters.
are the corresponding parameters.
Assume the network model is single user and single link. The dynamic buffer length at bottleneck is that
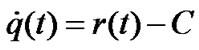 , (4)
, (4)
where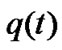 is the instantaneous queue length in buffer,
is the instantaneous queue length in buffer, 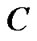 is link capacity.
is link capacity.
Let ,
,  , (3) and (4) can be described as
, (3) and (4) can be described as
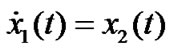 , (5)
, (5)
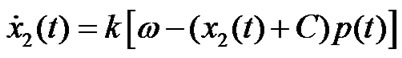 , (6)
, (6)
where is the reference queue length.
is the reference queue length.
The AQM algorithms based on control theory treat the queue length in router as a controllable state, and through a feedback mechanism adjust the probability of traffic drop or marker. In order to maintain the queue length at the desired value, then the system can get high link utilization and low time delay.
Our control objective is through design of the marker probability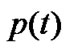 with
with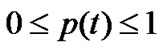 , obtain higher link utilization, low packet loss rate and small queue fluctuations.
, obtain higher link utilization, low packet loss rate and small queue fluctuations.
3. Design of Sliding Mode Control Algorithm
There are mainly two steps in the design of sliding mode control systems. One is the design of sliding surface, on which the system should get desired quality, such as asymptotically stable; The other is designing the sliding mode controller, which should guarantee the arriving condition.
3.1. Sliding Surface Design
First choose a sliding surface as conventional
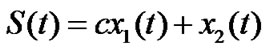 . (7)
. (7)
The objective of sliding mode control is to make the state slide to origin along the sliding surface in a finite time. That means the error of queue length is zero, and the sending rate and link capacity are totally matching.
When arrive at the sliding surface, , so
, so
 . (8)
. (8)
Substituting (8) into (5), we can obtain the sliding mode dynamics as follows
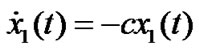 , (9)
, (9)
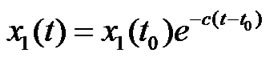 , (10)
, (10)
where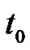 means the initial time. So the system motion on the sliding surface (7) can converge to the origin point in finite time if
means the initial time. So the system motion on the sliding surface (7) can converge to the origin point in finite time if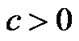 .
.
3.2. Sliding Mode Controller Design
Let , we can get the equivalent control law
, we can get the equivalent control law
 . (11)
. (11)
Apparently, this controller can make the system (5) (6) stable, but it can not satisfy the physical meaning of the marker probability . However (11) is helpful for us to design a more reasonable AQM controller
. However (11) is helpful for us to design a more reasonable AQM controller
 (12)
(12)
Theorem 1: If the control law (12) is used for system (5) and (6), the reaching condition is satisfied if .
.
Proof: When ,
,
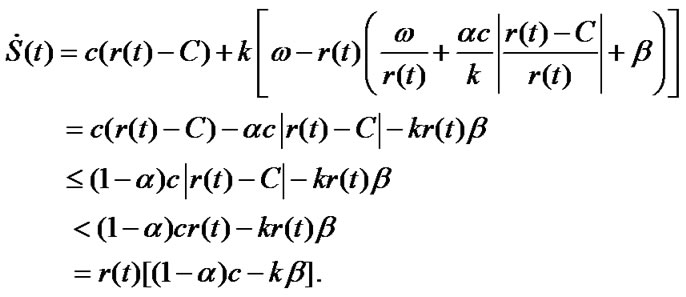
So if , choose
, choose  and the reaching condition
and the reaching condition 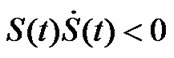 is satisfied.
is satisfied.
When ,
,

So if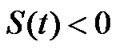 , choose
, choose  and the reaching condition
and the reaching condition 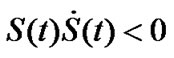 is satisfied too.
is satisfied too.
Theorem 2: The sliding mode dynamics (9) can converge to origin point after the time
 , (13)
, (13)
where 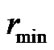 is the lowest sending rate.
is the lowest sending rate.
Proof: Choose a Lyapunov function candidate for (9) as follows
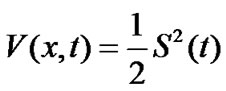 , (14)
, (14)
then the time derivative of V (t) along (9) is
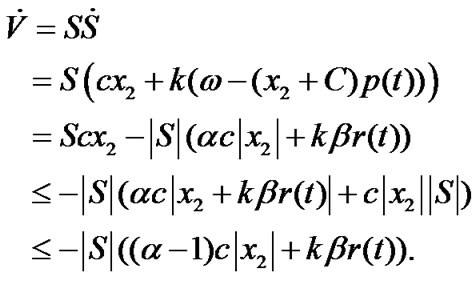 (15)
(15)
From Theorem 1 we can get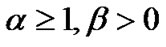 , so
, so
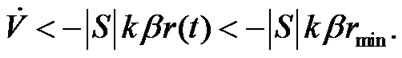 (16)
(16)
By (14), we have
 . (17)
. (17)
Substituting (17) into (16), we can obtain the following inequality
 , (18)
, (18)
then
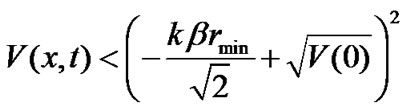 . (19)
. (19)
So we can get
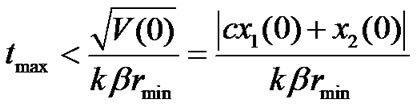 . (20)
. (20)
3.3. Simulation Results
In this section we validate the effectiveness and performance of the controller proposed in this paper by simulations. We consider the dumbbell network topology with a single bottleneck link in Figure 1.
Choose the parameters of network as follows: the maximum buffer of each router is 500 packets and the link capacity is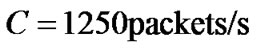 . The desired queue length
. The desired queue length 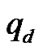 is 200 packets. The initial queue length is 400 packets. The PSMC-AQM controller parameters are
is 200 packets. The initial queue length is 400 packets. The PSMC-AQM controller parameters are
 ,
, 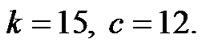
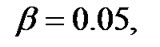 In order to
In order to
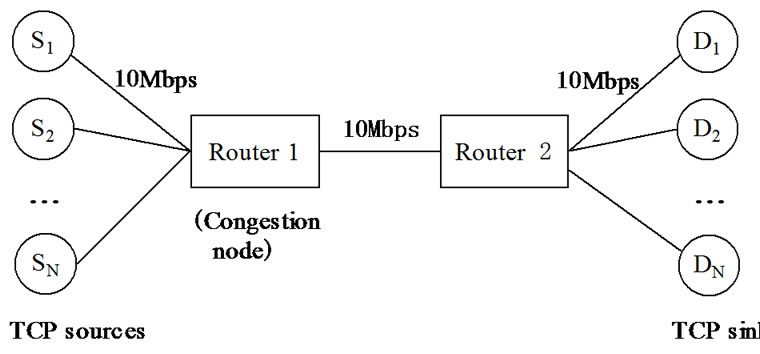
Figure 1. Simulation network topology.
reduce the chattering problem, a saturation function is used. The RED (Random Early Detection) algorithm is also simulated under the same network condition for the purpose of comparison. In addition, we use the parameters minimum 80packets and maximum 320packets.
Queue length, link utilization and data dropping between RED-AQM and PSMC-AQM are compared. Figure 2 and Figure 3 demonstrate that the PSMC-AQM controller considers not only the queue length but also the matching condition of the assemble rate and the link capacity, so it reflects the network condition better than RED. Both of the algorithms can control the queue length near the desired 200 packets, and PSMC-AQM get less data loss rate, so it makes higher link utilization rate. The results are showed in Table 1.

Figure 2. Average queue length using RED.
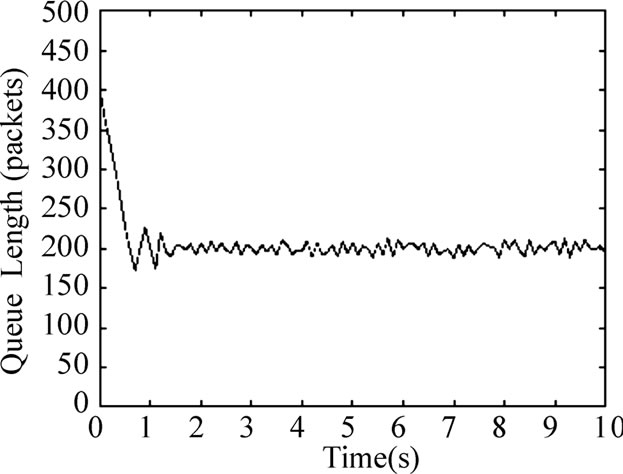
Figure 3. Average queue length using PSMC.

Table 1. Comparison between RED and PSMC.
4. Design of Terminal Sliding Mode Control Algorithm
Last section introduces sliding mode control into the optimization based internet congestion control model, and designs a linear sliding surface, and then validates the effectiveness of the algorithm in simulation. But the sliding mode along the sliding surface is asymptotically stable, that means the converging time could be quite long. For speediness is so important for a router algorithm, a special nonlinear sliding surface named terminal sliding surface is proposed in this section. The terminal sliding surface guarantees the finite reaching time to the sliding surface from initial states and the finite reaching time to the origin point. So the converging time is limited, and the speed of the sliding mode control system is enhanced, further the congestion control performance is improved.
4.1. Design of Terminal Sliding Surface
We design a nonlinear terminal sliding surface as follows:
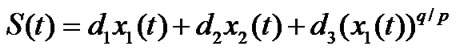 , (21)
, (21)
where  >0,
>0,  >0,
>0, 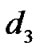 >0, p and q are odd positive integers and they satisfy q< p<2q. The sliding surface S(t) corresponds to a combination of the queue length error, the error between incoming traffic rate and link capacity.
>0, p and q are odd positive integers and they satisfy q< p<2q. The sliding surface S(t) corresponds to a combination of the queue length error, the error between incoming traffic rate and link capacity.
When the system state trajectories are on the terminal sliding surface, S(t) satisfies S(t) = 0. So we can obtain the following equality
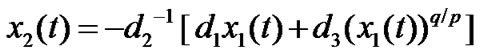 . (22)
. (22)
Substituting (22) into (5), we can obtain the sliding mode dynamics as follows:
 . (23)
. (23)
In order to prove that (23) can converge to the equilibrium point in finite time, we introduce a lemma as follows Lemma 1 [13]: Assume that a continuous, positive definite function V (t) satisfies the following differential inequality
 ,
, ,
, , (24)
, (24)
where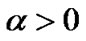 ,
, 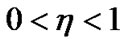 are constants. Then V(t) satisfies the following inequality:
are constants. Then V(t) satisfies the following inequality:
 ,
, (25)
(25)
and
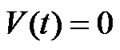 ,
,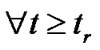 (26)
(26)
with 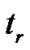 given by
given by
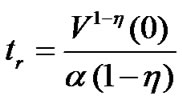 . (27)
. (27)
Theorem 3: The sliding mode dynamics (23) can converge to the equilibrium point after the time  and
and  satisfies
satisfies
 , (28)
, (28)
where is the initial value of
is the initial value of  and
and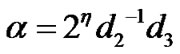 ,
, .
.
Proof: Choose a Lyapunov function candidate for the system (23) as follows:
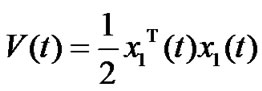 (29)
(29)
then the time derivative of V (t) along (23) is
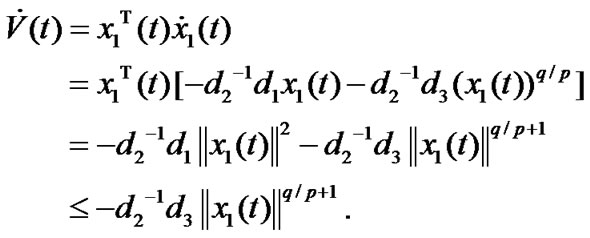 (30)
(30)
By (29), we have
 (31)
(31)
Substituting (31) into (30), we can obtain the following inequality
 (32)
(32)
where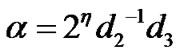 ,
,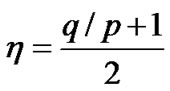 .
.
According to Lemma 1, we know that the sliding mode dynamics (23) can converge to the equilibrium point after the time  and
and 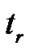 satisfies the following equality
satisfies the following equality
 (33)
(33)
So the system motion on the terminal sliding surface (21) can converge to the equilibrium point in finite time.
4.2. Design of Terminal Sliding Mode Controller
In the subsection, we design a robust terminal sliding mode controller to satisfy the reaching condition. We consider the following control structure of the form
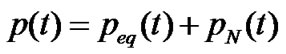 . (34)
. (34)
Theorem 4: If the control law is used for system (5) and (6) as follows:
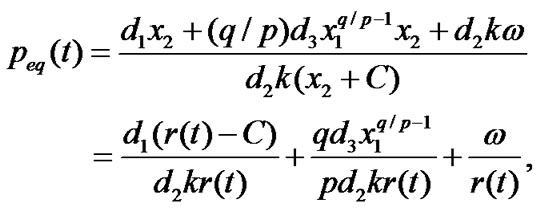 (35)
(35)
 (36)
(36)
then the controller can satisfy the reaching condition
 . (37)
. (37)
Proof : Recall (21), the time derivative of S(t) along the trajectory of (5) and (6) under the control (34) is given as
 (38)
(38)
Substitute (34) into (38), we can get
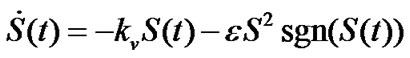 .
.
So the controller (34) can satisfy the reaching condition (37). That is to say, the controller can force system state trajectories toward the terminal sliding surface infinite time and maintain them on the sliding surface after then. Meanwhile, the reaching rate is fast and chattering is low.
4.3. Simulation Results
In this section the effectiveness and performance of the terminal sliding mode controller (TSMC) is validated by simulations. Common sliding mode controller (SMVS, Sliding Mode Variable Structure) is also simulated for the purpose of comparison with suggested parameter values ,
, ,
, 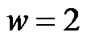 given in [15]. We consider the same dumbbell network topology with a single bottleneck link as Figure 1.
given in [15]. We consider the same dumbbell network topology with a single bottleneck link as Figure 1.
The network parameters are chosen the same as Part C of Section 3: the maximum buffer of each router is 500 packets and the link capacity is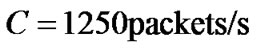 . The desired queue length
. The desired queue length 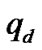 is 200 packets. The initial queue length is 400 packets. And the parameters of TSMC-AQM controller are chosen as
is 200 packets. The initial queue length is 400 packets. And the parameters of TSMC-AQM controller are chosen as ,
,  ,
, 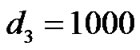 ,
,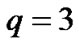 ,
,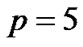 ,
,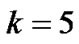 ,
,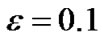 . From Theorem 3 we can calculate
. From Theorem 3 we can calculate  s.
s.
The simulation is operated under variable network conditions. The link capacity C and the roundtrip time R are varied through the process. Figure 4 and Figure 5 show that the two controllers are insensitive to different TCP loads and link capacity, but TSMC has shorter regulating time and better steady performance than SMVS controller.
5. Conclusions
In this paper, we combine the Kelly’s optimization scheme and the sliding mode control algorithm to analyze the convergence of the queue. We design two slid-

Figure 4. The comparison with variable C.
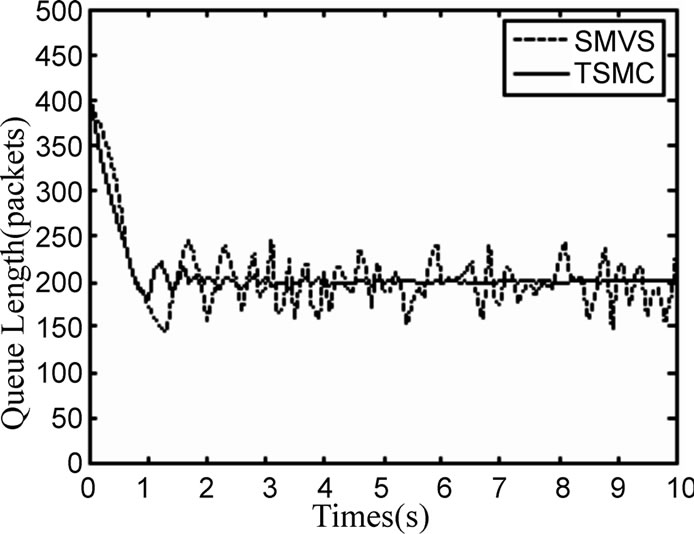
Figure 5. The comparison with variable![]() .
.
ing mode algorithm: the linear and the terminal ones. The simulation results show that both of the algorithms can converge to the equilibrium point in finite time. Obviously, the terminal sliding mode control can obtain faster transients and less oscillatory responses under dynamic network conditions, which translates into higher link utilization, low packet loss rate and small queue fluctuations. And the proposed controller has better stability and robustness than common sliding mode controller, which would be meaningful for the congestion control of the Internet.
6. References
[1] B. Braden and D. Clark, “Recommendations on queue management and congestion avoidance in the Internet,” RFC 2309, 1998.
[2] S. Floyd and V. Jacobson, “Random early detection gateways for congestion avoidance,” IEEE/ACM Transaction on Networking, Vol. 1, pp. 397-413, 1993.
[3] W. C. Feng, Kang G. Shin, D. D. Kandlur, et al., “The blue active queue management algorithms,” IEEE/ACM Transactions on Networking, Vol. 10, No. 4, pp. 513-528, 2002.
[4] S. Athuraliya, S. H. Low, V. H. Li, et al., “REM: Active queue management,” IEEE Network, Vol. 15, No. 3, pp. 48-53, 2001.
[5] S. Srisankar, Kunniyur, and R. Srikant, “An adaptive virtual queue (AVQ) algorithm for active queue management,” IEEE/ACM Transactions on Networking, Vol. 12, No. 2, pp. 266-289, 2004.
[6] C. V. Hollot, V. Misra, D. Towsley, and W. Gong, “On designing improved controllers for AQM routers supporting TCP flows,” Proceedings of IEEE INFOCOM, Anchorage, Alaska, USA, IEEE Communications Society, pp. 1726-1734, 2001.
[7] H. Lim, K. J. Park, and C. H. Choi, “Virtual rate control algorithm for active queue management in TCP networks,” IEEE Electronics Letters, Vol. 38, No. 16, pp. 873-874, 2002.
[8] F. Kelly, A. Maulloo, and D. Tan, “Rate control for communication networks: Shadow prices, proportional fairness and stability,” Journal of the Operational Research Society, Vol. 49, No. 3, pp. 237–252, March 1998.
[9] Y. H. Roh and J. H. Oh, “Robust stabilization of uncertain input-delay systems by sliding mode control with delay compensation,” Automatica, Vol. 35, pp. 1861- 1865, 1999.
[10] F. Y. Ren, C. Lin, and X. H. Yin, “Design a congestion controller based on sliding mode variable structure control,” Computer Communications, Vol. 28, pp. 1050- 1061, 2005.
[11] P. Yan, Y. Gao, and H. AOzbay, “A variable structure control approach to active queue management for TCP with ECN,” IEEE Transactions on Control Systems Technology, Vol. 13, pp. 203-215, 2005.
[12] F. J. Yin, G. M. Dimirovski, and Y. W. Jing, “Robust stabilization of uncertain input delay for Internet congestion control,” Proceedings of the American Control Conference, Minneapolis, Minnesota, USA, pp. 5576-5580, 2006.
[13] Y. Tang, “Terminal sliding mode control for rigid robots,” Automatica, Vol. 34, pp. 51-56, 1997.
[14] S. H. Yu, X. H. Yu, B. Shirinzadeh, and Z. H. Man, “Continuous finite-time control for robotic manipulators with terminal sliding mode,” Automatica, Vol. 41, pp. 1957-1964, 2005.
[15] F. Paganini, Z. Wang, J. C. Doyle, and S. H. Low, “Congestion control for high performance, stability, and fairness in general networks,” IEEE/ACM Transaction on Networking, Vol. 13, No. 1, pp. 43–56, 2005.
[16] R. Thommes and M. J. Coates, “Deterministic packet marking for congestion price estimation,” In Proceeding of IEEE Infocom, Hong Kong, pp. 12-23, 2004.

