Technology and Investment
Vol.2 No.3(2011), Article ID:7016,11 pages DOI:10.4236/ti.2011.23022
Optimization of Supply Chain Planning with Considering Defective Rates of Products in Each Echelon
1Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran
2Department of Engineering at Saipa Press Company, Institute of Management and Planning Studies, Tehran, Iran
3Department of Industrial Engineering, Branch of Science and Research, Islamic Azad University, Tehran, Iran
E-mail: {Behinelahi, Seyedhoseini}@yahoo.com, {Yaser.pakzad, Leila.etaati}@gmail.com
Received April 14, 2011; revised May 21, 2011; accepted May 30, 2011
Keywords: Supply chain management; Supply chain planning, mathematical model, Non-linear mixed integer programming, Fuzzy compromise programming
Abstract
Supply Chain Planning has recently received considerable attention in both academia and industry. The major targets of supply chain planning are to reduce production costs, risks, delays and maximize or improve profit, quality of product, customer service which result in increased competitiveness, more customer satisfaction and portability. In this study, a new bi-objective mathematical modeling for a four-echelon supply chain, consisting multi-supplier, assembler, distribution center and retailer, with considering the defective rates of products is proposed. Then, fuzzy compromise programming method is applied to solve the non-linear mixed-integer bi-objective model. Finally, a numerical example is given to illustrate application of the proposed algorithm and the efficacy and efficiency of that are verified through this section. It has been shown that such an approach can significantly help the managers to decide properly toward economic supply chain planning.
1. Introduction
Supply chain planning is one of the most vital decisions in today’s global market as companies are forced to gain a competitive advantage by focusing attention to their entire supply chain. The notable concentration in the supply chain planning related research in the last decade has been owing to its potential to improve the efficiency and efficacy of operations and reduce costs. In real world, variety of activities are involved in supply chain planning issue such as supplier selection, inventory management, purchasing and transportation of materials, components and finished products in a multi-echelon supply chain. Suppliers are the significant link to any supply chain and subsequently sourcing decision is one of the essential decisions to be taken at the planning stage. According to Chopra and Meindl (2007), inventory is recognized as one of the four major drivers in a supply chain (Figure 1). Most successful companies begin with a competitive strategy and then decide what their supply chain strategy ought to be. The supply chain strategy determines how the supply chain should perform with respect to efficiency and responsiveness. The supply chain must then utilize the three drivers to reach the performance level the supply chain strategy dictates and maximize the supply chain profit. Inventory is one of the key drivers of supply chain performance. It exists in the supply chain because of a mismatch between supply and demand. An important role that inventory plays in a supply chain is to increase the amount of demand that can be satisfied by having the product ready and available when customer wants it. Another significant role that inventory plays is to reduce cost by exploiting economics of scale that may exist during production and distribution. Inventory is held throughout the supply chain in form of raw material, work in process and final goods. Inventory is a major source of cost in supply chain and has huge impact on responsiveness.
Facility is another important driver of supply chain performance in terms of responsiveness and efficiency. For instance, companies can gain economies of scale when a product is manufactured or stored in only one location; this centralization increases efficiency. The cost reduction; however, comes at the expense of responsiveness, as many of a company’s customers may be located far from the production facility. The opposite is also true. Locating facilities close to customer increases the number of facilities needed and consequently reduces efficiency but improves the responsiveness.
Transportation is another significant driver to improve supply chain performance. It moves product between different stages in a supply chain. Like other drivers, transportation has a large impact on both responsiveness and efficiency. Faster transportation allows a supply chain to be more responsive but reduces its efficiency. The type of transportation a company uses also affects the inventory and facility locations in the supply chain.
Information is an essential driver that companies have used to become both more efficient and more responsiveness. The tremendous growth of the importance of information technology is a testimony to the impact that information can have on improving a company. Like all the other drivers; however, even with information, companies reach a point when they must make the trade-off between efficiency and responsiveness.
The responsiveness of the supply chain can be increased by high inventory levels although its cost efficiency decreases due to the cost of holding inventory [1]. Considering the aforementioned points, a relevant problem in supply chain planning is to determine the appropriate levels of inventory and lot size of ordering at the various stages involved in the system.
Regarding the supply chain management (SCM) and supply chain planning there are various approaches. A multi-objective production and distribution-scheduling scheme for a supply chain system is formulated by Chen et al. (2003) [2]. In this method, in addition to maximizeing profit for the entire system, fair profit distribution among all members, customer service levels, and safe inventory levels are taken into account simultaneously. Xiaoming Yan et al. (2010) extended the model of Coordination in decentralized assembly systems with uncertain component yields and proposed a new kind of contract, surplus subsidy contract, where the leader (the assembler) provides the contract, while the followers (component suppliers) make their choices simultaneously. They proved that the profit of the supply chain under coordination can be arbitrarily divided between the component suppliers and the assembler [3]. Ya-Ti Lin et al. (2010) proposed a novel hybrid MCDM technique (ANP Interpretive Structural modeling) in order to cope with the complex and interactive vendor evaluation and selection problem.They considered four main dimensions with definite criteria: delivery management capability, quality management capability, price and integrated service capability [4]. Darwish and Odah developed a model for a supply chain with single vendor and multiple retailers under VMI mode of operation [5]. Kang and Kim in 2009, considered a supply chain consisting of a single retailer and a single supplier [6]. Ming-Feng Yang and Yi Lin (2010) proposed a serial multi-echelon integrated just in-time (JIT) model based on uncertain delivery lead time of suppliers and quality unreliability in single product situation [7]. Cheng-Liang Chen and Wen- Cheng Lee (2004) considered supply chain scheduling issue by proposing a mixed-integer nonlinear programming problem to satisfy several conflict objectives, such as fair profit distribution among all participants and
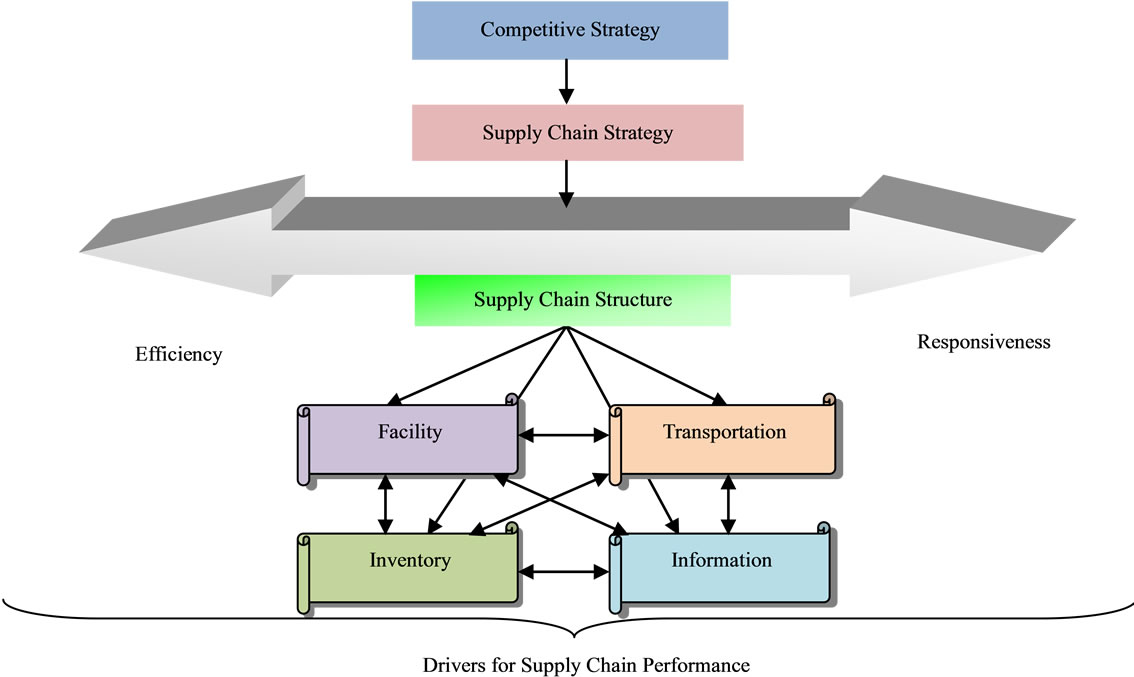
Figure 1. Four major drivers in a supply chain.
robustness of decision to uncertain product demands. They, also, modeled the uncertain market demands as a number of discrete scenarios with known probabilities and utilized the fuzzy sets are used for describing the sellers’ and buyers’ incompatible preference on product prices X[9] X.
S. A. Torabi and E. Hassini (2007) provided a supply chain master planning model consisting of multiple suppliers, one manufacturer and multiple distribution centers. They proposed a multi-objective possibilistic mixed integer linear programming model for integrating procurement, production and distribution planning by applying a two-phase interactive fuzzy programming procedure X[10] X. Although there exist several mathematical models for supplier selection, order quantity allocation and supply chain planning, most of these were developed to solve a single-period problem intended for short term planning (It is unmistakably axiomatic that, a single-period problem does not lead to an inventory policy for continuous replenishment over an infinite planning horizon). Moreover, in a real production environment, it can often be observed that there are defective items being produced. These defective items must be rejected, repaired, reworked, or, if they have reached the customer, refunded. In all cases, substantial costs are incurred. Therefore, it is more appropriate to take the quality-related cost into account in determining the optimal ordering policy.
Moreover, it is really worth to consider that the essence of inventory control is to balance the tradeoffs of inventory carrying, ordering and shortage costs. In other words, holding larger inventory results in higher carrying cost, but reduces the cost of ordering and backorders/lost sales. Consequently, as the implementation of JIT (JustIn-Time) practice becomes more and more widespread, each echelon in a supply chain tends to hold lower inventories, and may even incur deliberate shortages if it is cost efficient. Therefore, the whole supply chain is now made more vulnerable to lost sales and/or backorders. One of the purposes of this paper is to consider the inventory in a model in a way to be more relevant in today’s situation incorporating backorders and lost sales faced by upstream echelon of the supply chain (Here this echelon is related to retailers).
This paper deals with supply chain planning issue from the perspective of proposing an economic model in multi-period among various echelons of a supply chain with considering the defective rates of products. Also, in the case study that is presented, as an automotive supply chain (which has a serial system) is modeled dealing with defective rates of products in each echelon play essentiol roles. In order to model this problem, a multiechelon supply chain which contains various suppliers, assemblers, distribution centers (DCs) and retailers in multi-period are considered. Unlike the other paper, we have taken into account minimizing the two important objectives: total costs and defective rates of products. This model allows a serial system to select the proper set of suppliers while allocating their corresponding order quantities over time leading to an inventory policy with minimum total cost per time unit. Additionally, it considers a four-echelon supply chain and determines the lot-size for each echelon in different periods. Furthermore, we attempt to use a simple and effective method by having fuzzy approach toward compromise programming method to consider a trade-off between these two objective. Besides, another objective which is realted to the service levels at retailer is taken into account by incorporating it in constraints of the proposed model. The rest of the paper is organized as follows: Section 2 is related to the Mathematical formulations of the proposed model. Section 4 describes the solution method and entails different parts: concepts of fuzzy compromise programming approach, measuring the weights of criteria, choosing a suitable aggregate operator to determine a degree of global utility function, reformulating the MOLP into a fuzzy compromise programming model and solving the model up to optimality. In Section 5 a numerical example with solution is presented in order to illustrate the efficacy and efficiency of the proposed approach. Finally, in section 6 some conclusions and future research are presented.
2. Problem Description and Formulation
In this paper, in order to develop a comprehensive mathematical model for supply chain planning issue, unlike the other papers, it is taken into account that the supply chain has four echelons and entails multi-supplier, multiassembler, multi-distribution centers (DCs) and multiretailer (Figure 2). All considered costs are assumed to be known and accurately determined over the planning horizon. Two main objective functions will be optimized simultaneously: I) the first objective is minimizing the total costs of supply chain and II) the second one is minimizing the defective rate of components and products. Owing to the fact that the case study is performed in an automotive supply chain, considering these two objectives simultaneously are really essential.
It is assumed that, different kinds of components are flowed into assemblers’ plants from some selected suppliers. Then, variety of products will be provided by assembling different sets of components. Final products will be delivered to a set of distribution centers and consequently will be distributed among different retailers. End customers place their orders to these retailers. The demand of each product type is forecasted for the following T periods. In other words, in each period, customers’ demands are known and deterministic.
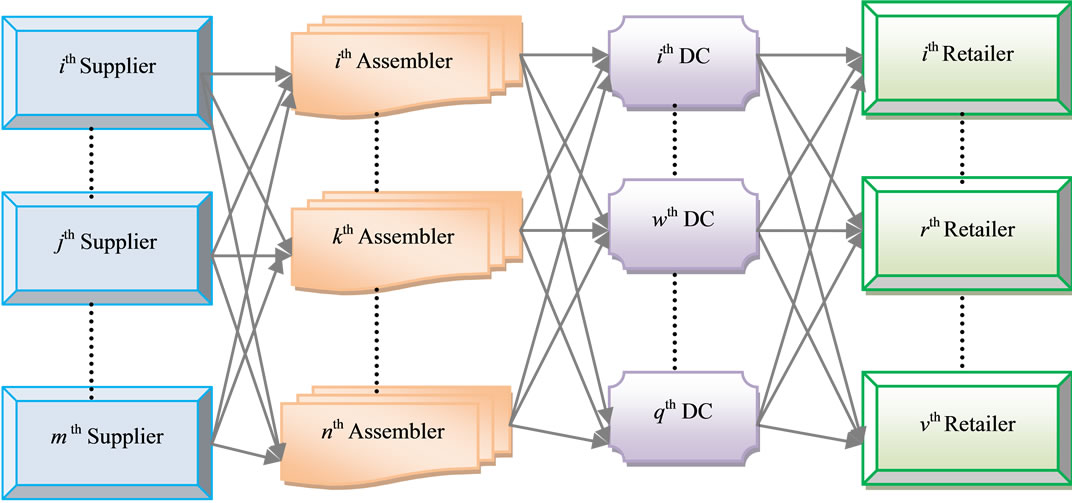
Figure 2. The schematic diagram of considered echelons in supply chain.
Each potential supplier has a definite and limited capacity for providing different components in each period and has the capability of procuring all kinds of components. Moreover, retailers are independent from each other and attempt individually to meet their own customers “demands” and it is assumed that distribution centers can hold inventory but retailers prefer not to hold any inventory. Assemblers are just capable of holding inventory related to variety of components for performing their processes. Also, there are capacity limitations for shipping products from assemblers to distribution centers and sequentially from distribution centers to retailers. Unlike the other paper, here, each retailer may encounter shortage in meeting customers “demands” and there is partial backordering for each type of product. This assumption also makes our proposed model distinct because in most of the papers full backordering is considered. Moreover, in this paper, the relationship among service levels at retailers sites, demands and back orderings is taken into consideration that plays an essential role in improving customer satisfaction levels. Now the list of indices, parameters and decision variables are introduced for problem formulation:
Considering the aforementioned assumptions and notations, the problem can be modeled as following:
First Objective:
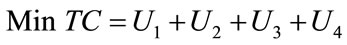 (1)
(1)
Second Objective:
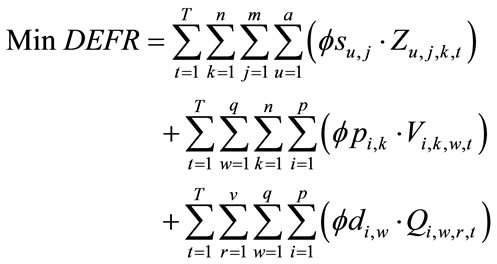 (2)
(2)
Subject to:
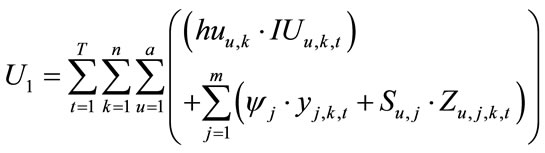 (3)
(3)
 (4)
(4)
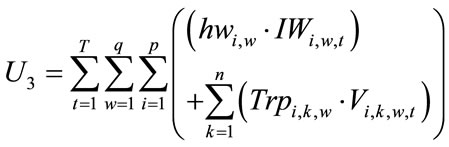 (5)
(5)
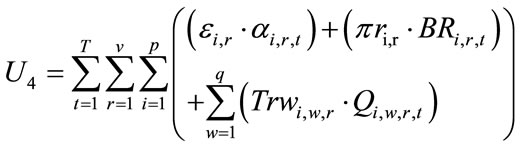 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
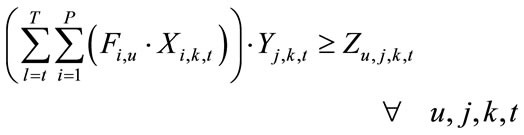 (10)
(10)
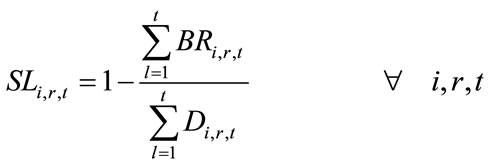 (11)
(11)
 (12)
(12)
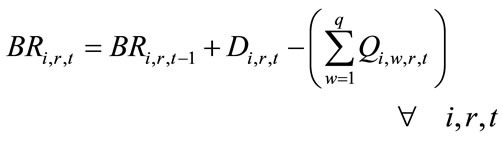 (13)
(13)
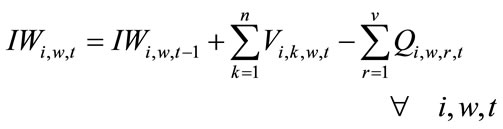 (14)
(14)
 (15)
(15)
 (16)
(16)
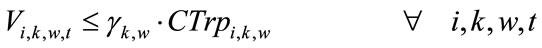 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
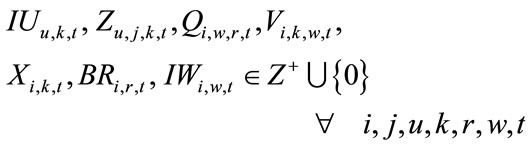 (22)
(22)
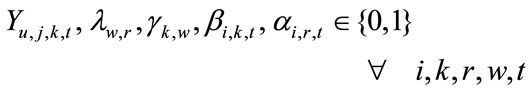 (23)
(23)
As it can be observed, in the proposed mathematical model, the first objective function (Equation (1)) demonstrates the considered total costs of supply chain. It includes four different parts: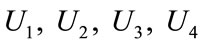 . Term
. Term  refers to the costs of components which include holding costs of inventory at assemblers’ sites, fixed ordering costs and purchased costs (Equation (3)). Term
refers to the costs of components which include holding costs of inventory at assemblers’ sites, fixed ordering costs and purchased costs (Equation (3)). Term 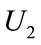 indicates on the assemblers costs which entails fixed costs of assembling, costs of regular time assembling and customization costs of components in assembling products (Equation 4). Term
indicates on the assemblers costs which entails fixed costs of assembling, costs of regular time assembling and customization costs of components in assembling products (Equation 4). Term 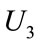 is related to distribution centers’ costs which consists of holding costs of inventory at distribution centers’ sites and transportation costs of products carrying from assemblers to distribution centers (Equation (5)). Term
is related to distribution centers’ costs which consists of holding costs of inventory at distribution centers’ sites and transportation costs of products carrying from assemblers to distribution centers (Equation (5)). Term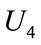 is associated with retailers costs that includes set-up costs of products at retailers’ sites per order, backordering costs of products at retailers’ sites and transportation costs of products carrying from distribution centers to retailers (Equation (6)). The second objective function (Equation (2)) refers to minimizing the defective rates of components delivered to assemblers by suppliers, defective rates of products delivered to distribution centers by assemblers and defective rates of products delivered to retailers by distribution centers. Balanced constraints related to components at assemblers plants are taken into account through Equation (7). Constraint (8) stands for the capacity limitation of suppliers for providing various components. Constraint (9) demonstrates the store capacity of assemblers for holding components. Constraint (10) certifies that there is not an order for procuring components without charging an appropriate transaction cost (ordering cost). The relationship among service levels at retailers’ sites, demands and back orderings are shown by Equation (11). Constraint (12) indicates that the value of decision variables “service levels” can vary between the values of parameter “SLmin” (minimum service level at retailers 'sites that are determined unanimously by retailers in order to meet their customers’ demand) and 1. Balanced constraints related to retailers and distribution centers’ sites are considered through Equations (13)-(14). Constraint (15) guarantees that in each period, each assembler ships all the produced final products to variety of distribution centers and doesn’t hold any inventory related to final products. Constraint (16) refers to the capacity limitation of transporting final products from distribution centers to retailers. Similarly, constraint (17) stands for the capacity limitation of carrying products from assemblers to distribution centers. Constraint (18) demonstrates the store capacity for holding products at distribution centers sites. Constraint (19) refers to this fact whether assembling of products sets up at assemblers plants or not. Correspondingly, constraint (20) denotes whether retailers place assembly order for products or not. Constraint (21) refers to the maximum capacity of assembling at assemblers’ plants. Moreover, forbidding negative continuous values for orders, amounts of inventory related to components at assemblers plants, amounts of producing final products, amounts of backordering and amounts of holding inventory at distribution centers site has been satisfied through constraint (22). Furthermore, constraint (23) sets the values of binary variables.
is associated with retailers costs that includes set-up costs of products at retailers’ sites per order, backordering costs of products at retailers’ sites and transportation costs of products carrying from distribution centers to retailers (Equation (6)). The second objective function (Equation (2)) refers to minimizing the defective rates of components delivered to assemblers by suppliers, defective rates of products delivered to distribution centers by assemblers and defective rates of products delivered to retailers by distribution centers. Balanced constraints related to components at assemblers plants are taken into account through Equation (7). Constraint (8) stands for the capacity limitation of suppliers for providing various components. Constraint (9) demonstrates the store capacity of assemblers for holding components. Constraint (10) certifies that there is not an order for procuring components without charging an appropriate transaction cost (ordering cost). The relationship among service levels at retailers’ sites, demands and back orderings are shown by Equation (11). Constraint (12) indicates that the value of decision variables “service levels” can vary between the values of parameter “SLmin” (minimum service level at retailers 'sites that are determined unanimously by retailers in order to meet their customers’ demand) and 1. Balanced constraints related to retailers and distribution centers’ sites are considered through Equations (13)-(14). Constraint (15) guarantees that in each period, each assembler ships all the produced final products to variety of distribution centers and doesn’t hold any inventory related to final products. Constraint (16) refers to the capacity limitation of transporting final products from distribution centers to retailers. Similarly, constraint (17) stands for the capacity limitation of carrying products from assemblers to distribution centers. Constraint (18) demonstrates the store capacity for holding products at distribution centers sites. Constraint (19) refers to this fact whether assembling of products sets up at assemblers plants or not. Correspondingly, constraint (20) denotes whether retailers place assembly order for products or not. Constraint (21) refers to the maximum capacity of assembling at assemblers’ plants. Moreover, forbidding negative continuous values for orders, amounts of inventory related to components at assemblers plants, amounts of producing final products, amounts of backordering and amounts of holding inventory at distribution centers site has been satisfied through constraint (22). Furthermore, constraint (23) sets the values of binary variables.
In the next section, fuzzy compromise programming is introduced in order to deal with solving this non-linear mixed-integer bi-objective mathematical modeling efficiently.
3. Solution Method
In this study, the concept of optimal compromise solution besides a simple fuzzy approach which applied by Li et al. (2000) toward a multi-objective transportation problem will be utilized to achieve a more reasonable compromise solution X[11] X. One of the advantages of this form of modeling is that the multi-objective problem has converted to a single objective programming problem and the ordinary optimization techniques can be used to solve it. Another advantage is related to this matter that employing fuzzy compromise programming can facilitate the generation of a more objective compromise solution by preventing the presence of non-homogeneous measuring scales among the two different objectives that are considered in supply chain planning system. At first a fuzzy approach to multi-objective problem will be introduced in order to obtain the degree of marginal utility for each objective. Secondly, by applying a proper combination of decision-making parameters, these degrees of marginal utility can be aggregated in order to achieve a global utility for all objectives. Thirdly, on the basis of obtained global utility, it will be possible to form a fuzzy compromise programming approach toward multi-objective problem. According to this consideration that the value of each objective function Zs changes linearly from 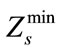 to
to 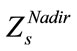 (which obtain by solving the multi-objective problem as a single objective, while ignoring the other objectives, and forming a pay-off table for all objective functions), it is possible to take into account this value as a fuzzy number with a linear membership function based on preference or utility. Also, the membership function of each objective utility can be defined by Equation (24).
(which obtain by solving the multi-objective problem as a single objective, while ignoring the other objectives, and forming a pay-off table for all objective functions), it is possible to take into account this value as a fuzzy number with a linear membership function based on preference or utility. Also, the membership function of each objective utility can be defined by Equation (24).
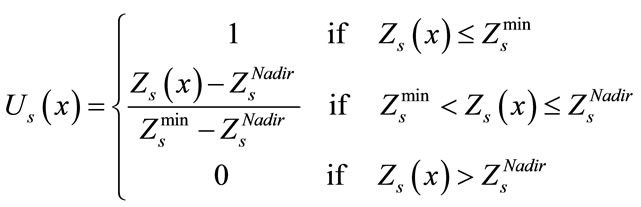 (24)
(24)
Moreover, we can define the degree of global utility 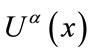 of the multi-objective problem as Equation (25).
of the multi-objective problem as Equation (25).
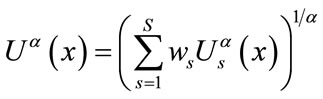
where:
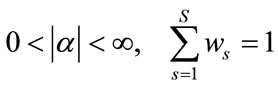 (25)
(25)
In Equation (25), 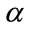 is a parameter and its value is determine in accordance with preference of decision makers. In practical perspective, normally two aggregation operators are applied to deal with the multi-objective problem. One of them maximizes the total utility expressed in terms of considering the sum of the utility of objectives and is defined as a weighted additive operator (
is a parameter and its value is determine in accordance with preference of decision makers. In practical perspective, normally two aggregation operators are applied to deal with the multi-objective problem. One of them maximizes the total utility expressed in terms of considering the sum of the utility of objectives and is defined as a weighted additive operator (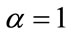 ). The other operator maximizes the least utility among all objectives, which is defined as a max-min operator (
). The other operator maximizes the least utility among all objectives, which is defined as a max-min operator (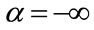 ). Moreover,
). Moreover,  represents the weight of sth criterion and demonstrates the decision makers’ preferences over the relative importance among the objectives and the way of its calculation will be discussed in the next section. Thus, the multi-objective problem stated in Equations (1)-(23), can be formulated as the following fuzzy compromise programming problem (Equation (26)).
represents the weight of sth criterion and demonstrates the decision makers’ preferences over the relative importance among the objectives and the way of its calculation will be discussed in the next section. Thus, the multi-objective problem stated in Equations (1)-(23), can be formulated as the following fuzzy compromise programming problem (Equation (26)).
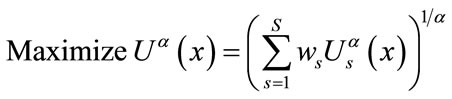 (26)
(26)
Subject to: X Let 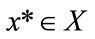 be an optimal solution for this model (Equation (26)). That is
be an optimal solution for this model (Equation (26)). That is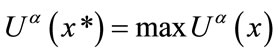 : (
: ( ).
). is a non-dominated (Pareto) compromise solution in which the synthetic membership degree of optimum for all objectives is maximal. In this paper, it is assumed that there are L decision makers (DMs) who have similar importance. They state their opinion toward relative importance of objectives via pair-wise comparison matrix. One analytical approach often suggested for solving a complex problem is AHP, first introduced by Saaty in 1980. It has been applied in a wide variety of decision-making contexts. It also provides a structured approach for determining the weights of criteria. Here, by employing such an extended pair wise comparisons, appropriate set of weights will be generated, owing to this fact that the relative importance of various objectives is considered. Consequently, more reasonable solutions will be obtained.
is a non-dominated (Pareto) compromise solution in which the synthetic membership degree of optimum for all objectives is maximal. In this paper, it is assumed that there are L decision makers (DMs) who have similar importance. They state their opinion toward relative importance of objectives via pair-wise comparison matrix. One analytical approach often suggested for solving a complex problem is AHP, first introduced by Saaty in 1980. It has been applied in a wide variety of decision-making contexts. It also provides a structured approach for determining the weights of criteria. Here, by employing such an extended pair wise comparisons, appropriate set of weights will be generated, owing to this fact that the relative importance of various objectives is considered. Consequently, more reasonable solutions will be obtained.
Let 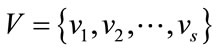 be a set of objectives. Each decision maker’s pair-wise comparison matrix (which is a reciprocal matrix) can be defined as Equation (27).
be a set of objectives. Each decision maker’s pair-wise comparison matrix (which is a reciprocal matrix) can be defined as Equation (27).
Also, Table 1 demonstrates the measurement scale which is used for verbal judgment or preference of DMs.
Moreover in order to aggregate DMs’ opinion, Geometric mean operator is applied and a single matrix is formed (Equation (28)).

Table 1. Measurement scale for verbal judgment or preference.
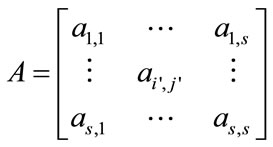 (27)
(27)
where:
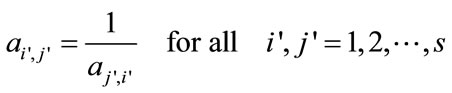
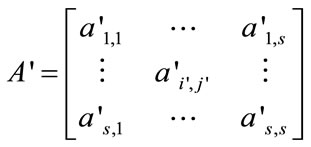 (28)
(28)
where:

for all 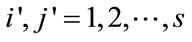 and
and .
.
Furthermore, in order to calculate the weights of criteria, referring to Saaty’s theorem that is shown by Equation (29) and his proposed heuristic method, for each row of matrix  the sum of elements is obtained and the weights are computed [12].
the sum of elements is obtained and the weights are computed [12].
 (29)
(29)
where A is a pair-wise matrix, W is the normalized principal right eigenvector of matrix A and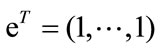 .
.
Therefore, after computing the weights of objectives, every parameters in the fuzzy compromise programming is definite and Equation (30) indicates on the extended form of this model (when the value of 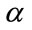 is assumed equal 1.
is assumed equal 1.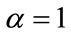 )
)
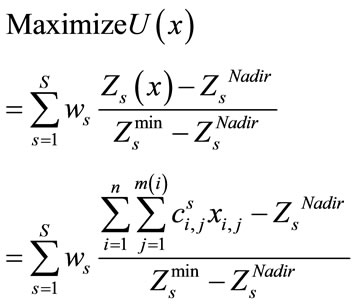
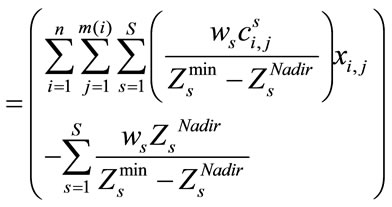 (30)
(30)
Subject to: 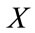
In the next section, in order to illustrate the efficacy and efficiency of proposed model and solution, a numerical example is applied for a data set.
4. Numerical Example
Consider a supply chain system with four echelons containing three suppliers, three assemblers, three distribution center and three retailers. There are three different components which are applied to form three finished products. It is assumed that the supply chain planning will be determined for three periods. This real numerical example which is related to an automotive supply chain has been formulated by using the proposed mathematical model (Equations (1)-(23)) and then has been solved by utilizing the fuzzy compromise programming solution procedure. LINGO software is applied (ran on an Intel Core 2 Duo 2.8 GHz PC) to form the pay-off table related to the three objective functions. The result of this stage is shown in Figures 3-4 and Table 3. In this table, each column is related to the different value of objective Zs by setting the optimum solution of other objective functions, also the minimum value of each objective function (disregarding other objective functions) has been bold.

Figure 3. The output of solving model by considering the first objective.
Considering the result of Table 2, we can identify the values of 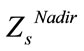 for s = 1, 2 as below:
for s = 1, 2 as below:
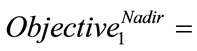 ,
,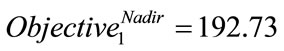 .
.
In this stage the marginal utility of each criterion is formed and the pair-wise comparison matrixes related to the two objectives are obtained through collecting three decision makers’ opinion. Also, the Geometric mean operator is utilized to aggregate their preferences. (In the pair-wise matrixes, sth objective (for s = 1, 2) indicates on total cost and defective rates of products, in order.) Besides, the weights of objectives are calculated.
|
|
|
|
|
|
|
|
|
Then, by assuming 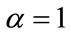 (Using weighted additive operator), the global utility in accordance with Equation 30 is formulated and the fuzzy compromise programming model is constructed.
(Using weighted additive operator), the global utility in accordance with Equation 30 is formulated and the fuzzy compromise programming model is constructed.

Subject to: 
After solving the reformulated mathematical model, the achieved results related to the value of utility function and the two objectives are shown through Table 3. Terms U1 and U2 show the extent of closeness related to the achieved values for objective1 and objective2 to their optimal values which obtained by solving the multi-objective problem as a single objective, while ignoring the other objectives.
Figure 4. The output of solving model by considering the second objective.
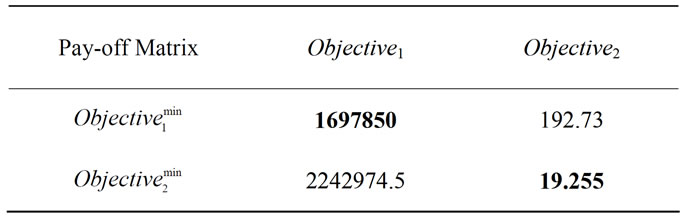
Table 2. Pay-off Matrix related to the two objectives.

Table 3. Achieved values for utility function and the two objectives.
Moreover, variety of values which are obtained for service levels at retailers’ sites (R1, R2 and R3) for each type of products (F, G or H) in each period (1, 2 or 3) are demonstrated through Figure 5. As the weight of the first objective has been more than the weight of the second objective in the multi objective mathematical modeling, the values of service levels that are achieved by the utility function (which is substituted for the two objecttives and has taken into account the weights of objectives efficiently) are more similar to the values of service levels obtained by considering the first objective separately rather than the values of service levels computed by taking into account of second objective independently.
5. Conclusions and Future Research
Nowadays, variety of factors in today’s global market has forced companies to gain a competitive advantage by focusing attention to their entire supply chain. Of the various activities involved in supply chain management, integrative planning among various echelons of a supply chain is one of the most strategic because it provides opportunities to reduce costs and consequently increase profits. In this paper, it is attempted to propose an efficient model for supply chain planning. Two major objectives, minimizing the total costs of supply chain and minimizing the defective rates to products were considered and the proposed mathematical model solved by applying Fuzzy compromise programming. Moreover, the achieved result of numerical example verifies the efficacy of that. Such a kind of modeling and solution method, can prepare an efficient opportunity for managers to decide properly for splitting orders among various suppliers while there are variety of products. Regarding this proposed model developing an optimal solution in large scales seems difficult. Also, if achieving a set of various solutions becomes available, decision makers can evaluate the pros and cons of each solution considering variety of qualitative or technical parameters in real situation in order to somehow overcome the uncertainty of environment. Therefore, according to the aforementioned points, it can be stated that this supply chain planning model involves a complex shape of search space with many candidate solutions. Thus, meta-heuristic methods such as genetic algorithm (GA) are applicable for fast exploration and can be considered as an efficient research in future. Also, dealing with variety of robust opti-
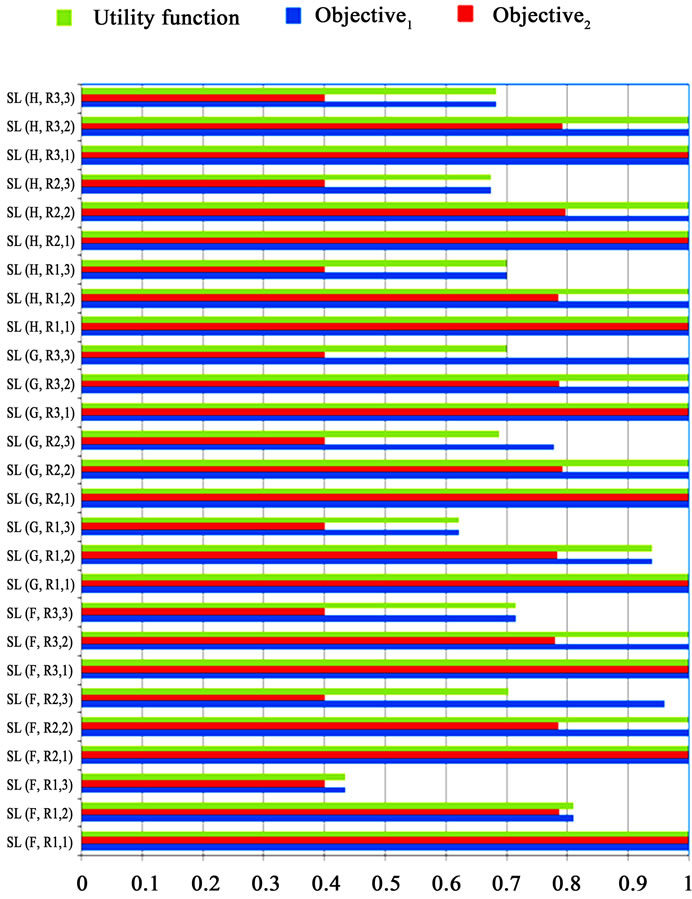
Figure 5. Various values of service levels by objective1, objective2 and utility function.
timization toward the proposed mathematical model can be taken into account as the other future research.
6. References
[1] S. Chopra and P. Meindl, “Supply Chain Management: Strategy, Planning, and Operations,” Prentice Hall, Upper Saddle River, 2007.
[2] L. Cheng, E. Subrahmanian and A. W. Westerberg, “Design and Planning under Uncertainty: Issues on Problem Formulation and Solution,” Computer and Chemical Engineering, Vol. 27, No. 6, 2003, pp. 781-801. doi:10.1016/S0098-1354(02)00264-8
[3] X. Yan, M. Zhang and K. Liu, “A Note on Coordination in Decentralized Assembly Systems with Uncertain Component Yields,” European Journal of Operational Research, Vol. 205, No. 2, 2010, pp. 469-478. doi:10.1016/j.ejor.2009.12.011
[4] Y. T. Lin, C. L. Lin, H. C. Yu and G. H. Tzeng, “A Novel Hybrid MCDM Approach for Outsourcing Vendor Selection: A Case Study for a Semiconductor Company in Taiwan,” Expert Systems with Applications, Vol. 37, No. 7, 2010, pp. 4796-4804. doi:10.1016/j.eswa.2009.12.036
[5] M. A. Darwish and O. M. Odah, “Vendor Managed Inventory Model for Single-Vendor Multi-retailer Supply Chains,” European Journal of Operational Research, Vol. 204, No. 3, 2010, pp. 473-484. doi:10.1016/j.ejor.2009.11.023
[6] J. K. Kang and Y. D. Kim, “Inventory Replenishment and Delivery Planning in a Two-Level Supply Chain with Compound Poisson Demands,” The International Journal of Advanced Manufacturing Technology, Vol. 49, No. 9-12, 2009, pp. 1107-1118.
[7] M. F. Yang and Y. Lin, “Applying the Linear Particle Swarm Optimization to a Serial Multi-echelon Inventory Model,” Expert Systems with Applications, Vol. 37, No. 3, 2010, pp. 2599-2608. doi:10.1016/j.eswa.2009.08.021
[8] W. Xia and Z. Wu, “Supplier Selection with Multiple Criteria in Volume Discount Environments,” Omega-International Journal of Management Science, Vol. 35, No. 5, 2007, pp. 494-504. doi:10.1016/j.omega.2005.09.002
[9] C. L. Chen and W. C. Lee, “Multi-objective Optimization of Multi-echelon Supply Chain Networks with Uncertain Product Demands and Prices,” Computers and Chemical Engineering, Vol. 28, No. 6-7, 2004, pp. 1131-1144. doi:10.1016/j.compchemeng.2003.09.014
[10] S. A. Torabia and E. Hassini, “An Interactive Possibilistic Programming Approach for Multiple Objective Supply Chain Master Planning,” Fuzzy Sets and Systems, Vol. 159, No. 2, 2008, pp. 193-214. doi:10.1016/j.fss.2007.08.010
[11] L. Li and K. K. Lai, “A Fuzzy Approach to the MultiObjective Transportation Problem,” Computer and Operations Research, Vol. 27, No. 1, 2000, pp. 43-57. doi:10.1016/S0305-0548(99)00007-6
[12] T. L. Saaty and J. M. Katz, “How to Make a Decision: The Analytic Hierarchy Process,” European Journal of Operational Research, Vol. 48, No. 1, 1990, pp. 9-26.