Received 12 June 2014; revised 8 July 2014; accepted 1 August 2014

ABSTRACT

Both theory and experiments indicate that the vacuum is not a state of empty space, but is populated by electromagnetic fluctuations at a lowest nonzero level, the Zero Point Energy (ZPE). This debouches into considerable changes of fundamental physics, as shown by a revised quantum electrodynamic theory (RQED) applied to elementary particles, and by a revised ZPE frequency spectrum applied to the expanding universe. The Standard Model based on a vacuum state of empty space is thus replaced by RQED, thereby resulting in massive elementary particles from the beginning, independently of the theory by Higgs. Also the basic properties of the Higgs-like particle detected at CERN can be reproduced by RQED. It further leads to new fundamental results beyond the theories by Dirac and Higgs, such as to a deduced value of the elementary net charge, magnetic confinement of charged particle configurations, intrinsic local particle charges, photon spin with a very small but nonzero photon rest mass, and needle-like particle-wave properties which contribute to the understanding of the photoelectric effect and two-slit experiments. The real macroscopic pressure due to the revised ZPE frequency distribution further influences the dynamics of the expanding universe, by the ZPE photon pressure gradient acting as dark energy, and the ZPE photon energy density acting as dark matter. This results in a model being consistent with the observed scale, the rate of expansion, and the stability of a flat expanding observable universe.

Keywords:

Zero Point Energy, Quantum Electrodynamics, Standard Model and Beyond, Expanding Universe, Dark Energy, Dark Matter

1. Introduction

As shown in reviews of quantum mechanics by Pauling and Wilson [1] and Schiff [2] among others, the solutions of the one-dimensional harmonic oscillator do not only lead to the Planck electromagnetic wave energy but also to a lowest nonzero energy level of one-half quantum per state, i.e. the Zero Point Energy (ZPE). Consequently, the vacuum state is not merely that of an empty space. It includes quantum fluctuations part of which also carry electric charges, as pointed out by Abbot [3] . An example of these fluctuations was given by Casimir [4] who predicted that two metal plates will attract each other when being sufficiently close together. This is due to the fact that only small wavelengths of the fluctuations can exist in the spacing between the plates, whereas the full spectrum exerts a net force on the outsides of the plates. The same force was first demonstrated experimentally by Lamoreaux [5] , in using a sensitive torsional pendulum. Its relation to the ZPE was already realized by Casimir [4] , and further elucidated by Milonni [6] in a review. This important and experimentally confirmed result thus reveals the existence of a real macroscopic Casimir pressure and energy density originating from the ZPE.

At his time, Casimir made the modest conclusion that his discovered “zero point pressure of electromagnetic waves might be of a certain interest”. Nevertheless later investigations indicate that the consequences of ZPE will debouch into considerable changes of fundamental physics, thereby removing severe limitations and weak points of the Standard Model of elementary particles.

The present review demonstrates some of the consequences which originate from the Zero Point Energy, as outlined in Figure 1 and based on recent investigations by the author. The latter deal with the physics of the smallest elementary particles being treated in terms of a revised quantum electrodynamic theory (RQED) [7] [8] , as well as the physics of the largest cosmical phenomena treated by means of a revised frequency distribution of the ZPE vacuum fluctuations [9] . For detailed deductions reference is made to the publications mentioned in this review.

2. Revised Quantum Electrodynamics

2.1. General Features of the Field Equations

The present field equations are of the general four-dimensional Lorentz invariant form [10]

(1)

here 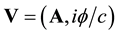is a four-potential with A as a three-dimensional magnetic vector potential, as an electrostatic potential, c standing for the velocity constant of light with, being a four- current density with j as a three-dimensional current density, and as an electric charge density. SI units are being used.

The special case leads to the d’Alembert equation of an empty vacuum state. Then there are no local sources of the electromagnetic field, and there is no scope for a local energy density in a steady state which is the condition for particle models with nonzero rest mass and with electric charge. This is supported by a statement by Quigg [11] which implies that the symmetry of the conventional field equations of the Standard Model makes them strongly restricted and does not permit masses for leptons and quarks.

Under the more general conditions of a nonzero current density J, and an associated nonzero electric charge density, there is a substantial change and an increased scope of the solutions originating from the field Equation (1). Since J has to become invariant in a transition from one inertial frame to another frame, the form of J should satisfy the condition

(2)

Further, since J has to vanish when there is no charge density, the final form of J becomes [7]

(3)

where C is a velocity vector in three-space. This can be regarded as a generalization of the Lorentz invariance from one to more dimensions, such as from plane to cylindrical waves. In a three-dimensional representation the extended field Equation (1) in the vacuum then become

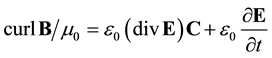(4)

(5)

(6)

(7)

(8)

thus being characterized by a broken symmetry between the electric and magnetic field strengths E and B. As compared to the conventional equations, the new features of these equations are represented by the space-charge current density of the first term in the right-hand member of Equation (4), and of Equation (8).

These equations are also gauge invariant, because the new contributions include the electric field strength E. As in conventional electromagnetic theory, they can be treated in an analogous way in a gauge transformation of the potentials A and.

The general properties of the field Equations (4)-(8) can now elucidate the connections between a nonzero div E and a nonzero ZPE. The questions on a revised spectral distribution of ZPE are postponed to Section 3. Here it is observed that steady electromagnetic states become possible through the source term of the space-charge current density in Equation (4), i.e. also when. There is then a nonzero energy density of the alternative form

(9)

including the charge density. All basic features of ZPE can thus be reproduced by a nonzero local div E as follows:

・ Local electrically charged as well as neutral electromagnetic fluctuations generated by this source.

・ Net total electric charges as well as vanishing net charges of spatially integrated particle models.

・ Intrinsic local charges of both polarities arising within limited regions of the particle models.

・ A nonzero spatially integrated total field energy and rest mass of such models.

As described by Schiff [2] among others, Maxwell’s equations are used as a guideline for proper interpretations of the conventional quantum electrodynamic theory. This also applies to the present extended equations. Here a short-cut and simplification will be made, by first determining the general solutions of the same equations, and then imposing relevant quantum conditions. This is at least justified by the fact that the quantized equations become identical to the original equations in which the potential V and current density J are merely being replaced by their expectations values, as shown by Heitler [12] . Such a way of handling the quantum conditions should therefore not be too far from the truth, by using the most probable trajectories and states in a first approximation.

It may finally be mentioned that, in a speculation by the author about a generalized law of gravitation, the latter is proposed to be extended to full symmetry. Such a law would include both polarities of corresponding charge and attractive as well as repulsive gravitational forces, in analogy with the Coulomb interaction [7] . An additional question would then follow, i.e. whether states of positive and negative mass could become associated with those of matter and antimatter.

2.2. New Fundamental Results of RQED

At this point more detailed descriptions can be given on the results which come out of the basic field equations, in respect to steady as well as time-dependent states.

2.2.1. Steady Electromagnetic States

Steady axisymmetric states representing particle models in a frame of spherical coordinates, with all relevant quantities being independent of the angle φ, lead to a current density and a magnetic vector potential. Here represents the two spin directions. The general solutions can then be expressed in terms of a generating function

(10)

where G₀ stands for a characteristic amplitude, G is a normalized dimensionless part, and with r₀ as a characteristic radial dimension. This yields the general solutions

(11)

(12)

(13)

with the operator where

. (14)

These solutions lead to charged and neutral particle models of both matter and antimatter, having spin and rest mass. This is in conformity with the equation by Dirac which includes the elementary charge “e” and the electron mass “m_e”, but as given and assumed parameters [10] . The mass m_e is then associated with a nonzero spin.

Among the special results which come out of the present RQED theory, the following can be mentioned:

・ The theory by Higgs is based on a spontaneous nonlinear mechanism of symmetry breaking in an empty vacuum state, by which an unstable boson of unspecified but large rest mass is being formed. This particle then decays into a succession of massive elementary particles. In the present RQED theory the source due to the space-charge current density results in elementary particles with rest mass, already from the beginning [8] [13] [14] . It is characterized by intrinsic linear broken symmetry. This provides an alternative explanation of the Higgs-like particle observed at CERN [15] - [17] .

・ The present theory yields a model of the Z boson having an effective radius of about 10⁻¹⁸ m, in agreement with measurements [14] . The decay of a Higgs-like boson into two Z bosons further initiates the idea of superimposing two Z bosons to form a model of such a particle. The resulting composite particle solution is consistent with the point made by Quigg [11] that the Higgs is perhaps not a truly elementary particle, but is built out of as yet unobserved constituents. Thereby the present theory on a Higgs-like boson satisfies the basic properties of the particle observed at CERN [16] [17] , in having vanishing charge, vanishing spin, an effective radius of about 10⁻¹⁸ m corresponding to a rest mass of about 125 GeV, and an unstable behavior due to its purely electrostatic nature [13] [14] .

・ With a separable generating function of Equation (10), the spatially integrated net electric charge q₀ and magnetic moment M₀ of a particle-shaped state become subject to a number of symmetry properties. These are due to the convergence or divergence of R(ρ) at the origin ρ = 0, and the top-bottom symmetry or antisymmetry of T(θ) in respect to the equatorial plane. Thus a divergent R(ρ) in combination with top-bottom symmetry of T(θ) is the only case leading to a charged particle such as the electron with q₀ ≠ 0 and M₀ ≠ 0, whereas q₀ = 0 and M₀ = 0 in all other cases, such as for a model of the neutrino [7] .

・ As described by Ryder [18] among others, the conventional divergence problem of infinite self-energy in point-charge-like geometries is tackled in a process of renormalization, by adding extra ad hoc counter terms to the Lagrangian. In this way a finite result is obtained from the difference between two “infinities”. In the present theory, the model of a charged particle is on the other hand treated in terms of a revised renormalization procedure, applied to the radial part R(ρ). Thereby the “infinity” of the latter is outbalanced by the “zero” of a “counter-factor”. This results in finite values of the net charge q₀, magnetic moment M₀, rest mass m₀, and spin s₀, associated with a very small characteristic radius of the model. In this way the problem of infinite self-energy can thus be tackled, as shown in more detail by the author [7] [19] and by Lehnert and Höök [20] . This revised process then has the result that all quantum conditions and all relevant experimental values of charge, magnetic moment, mass, and spin of the leptons can be reproduced by the choice of only two scalar free parameters, the so called first and second counter-factors.

・ In a variational analysis the absolute value of the deduced net elementary charge is found to fall within a narrow parameter range, positioned around the experimental value “e” and having the width of only a few percent of “e”, as shown by Lehnert and Scheffel [21] and Lehnert and Höök [19] [20] .

・ In the present theory a confining magnetic field prevents the charged leptons from “exploding” under the action of their electrostatic eigenforce [7] [20] .

・ In the RQED lepton models there also exist local intrinsic charges of both polarities, being an order of magnitude larger than the net elementary charge “e”. The resulting Coulomb interaction becomes about two orders of magnitude larger than that due to the net charge. If such conditions would also hold true for quarks, this total Coulomb force would become comparable and similar to the short-range strong force. This raises the question whether the intrinsic charge force will interfere with the strong force, or even become identical with it, as stated in a speculation by the author [22] .

2.2.2. Time-Dependent Electromagnetic States

With the field Equations (4)-(8) including an explicit time dependence, the wave-particle dualism will become an intrinsic property of the resulting solutions. A physically relevant photon model should have the form of a wave or wave packet of preserved and limited geometrical shape, propagating in an undamped way and in a defined direction. No artificial boundaries have to be imposed. The angular momentum in the direction of propagation, the spin, should have the constant value. This leads to the representation in a cylindrical frame with z in the direction of propagation. The velocity vector in Equation (4) then has the form

(15)

leading to the dispersion relation

(16)

for a normal wave of the form being associated with the photon mode. Here, and the spin is provided at the expense of a very small reduction of the phase and group velocities v from the value c.

Some specific results can here be mentioned as follows [7] :

・ The Standard Model leads to a vanishing total (integrated) spin of the individual photon [23] , in contradiction with experiments. This is shown in terms of the quantized solutions obtained from the d’Alembert equation in an empty vacuum state. The present theory of a cylindrical wave-packet model results on the other hand in a spin, as well as in an extremely small but nonzero rest mass. The phase and group velocities are then hardly distinguishable from the velocity constant c. As an example, for a photon wave packet of a relevant and small characteristic radial dimension, the reduction of the velocity v in Equation (16) with respect to c occurs first in the tenth decimal. The photon spin and photon rest mass are mutually related, due to the generalized Lorentz invariance.

・ For the individual photon both a particle behaviour in the form of needle-like radiation and a wave behaviour in the form of interference phenomena can simultaneously be realized [24] . This satisfies the necessary criteria for the observed behaviour of the photoelectric effect and that in two-slit experiments.

・ The present theory on screw-shaped wave modes is consistent with the observed hollow geometry of cork- screw-shaped light beams [25] .

・ The detected angular momentum of a light beam having a spatially limited cross-section can be explained by spin contributions from its boundary layers [26] .

・ The nonzero electric field divergence leads to intrinsic electric charges of alternating polarity within an individual photon wave packet. This contributes to the understanding of electron-positron pair formation.

・ Introducing the alternative form

(17)

of the velocity vector with α > 0, the dispersion relation becomes

(18)

for a superluminal normal tachyon mode [7] . This mode and resulting relations become identical with those of the earlier elaborated tachyon theory given in reviews by Recami [27] and Bilaniuk, Deshpande and Sudarshan [28] .

・ One surprising consequence of quantum mechanics has been the entanglement of two or more distant particles. This has raised the alternative question of nonquantum teleportation as stated by Rabounski and Borissova [29] . At a first sight, the superluminal tachyon mode of large α in Equation (18) may be considered as a candidate for this purpose. Since the basic field Equations (4)-(8) with C² = c² apply both to expressions (15) and (17) for the photon and tachyon modes, a transition between these modes could be imagined in terms of the Complementarity principle of the Copenhagen school by Bohr. However, this has to be considered as an open question needing further analysis, because superluminal speeds of the tachyons cannot be registered by a regular observer as anything but a motion at the speed of light, as stated by Rabounski and Borissova [29] .

3. Revised ZPE Frequency Distribution

3.1. A Self-Consistent Distribution

On account of the Casimir effect, the low-frequency part of the ZPE distribution has to be accepted as an experimental fact, but there exists a crucial problem with the high-frequency part. As demonstrated by Terletskii [30] , Milonni [6] and Loudon [31] among others, conventional theory results in a spectrum having an infinite total (integrated) energy density. Such a result is unacceptable, both from the physical point and from the point that the analysis is underdetermined and treats the included infinite number of states with the same statistical probability.

Several attempts have been made to truncate the involved integral at cut-off frequencies corresponding either to the Planck length or to an arbitrarily high energy of 100 GeV. This still leads to an excessive vacuum energy density being about 10¹²⁰ or 10⁵⁵ times greater than that being expected. There are also several investigators such as Riess and Turner [32] and Heitler [12] who have thrown doubt upon the conventional theory.

To overcome these difficulties, the author has proposed that the ensemble of ZPE energy modes (photons) requires a separate treatment, also at the temperature limit T = 0, which first become self-consistent when the system is defined to have a given and finite total energy density [9] [33] - [35] . Such an analysis can be conducted in the standard way of an ensemble of ZPE photons with the frequency and energy, populating the available states in statistical equilibrium with a probability given by the Bolzmann factor, where is the average particle energy of the ensemble. Then the energy density within the frequency range becomes

. (19)

which results in a total and local energy density

. (20)

here the average frequency is a so far arbitrary quantity, in the same way as the mean energy kT of the Planck distribution, and can also depend on its local position in the universe. The energy density in Equation (20) thus yields a finite total ZPE vacuum pressure.

This revised frequency distribution further leads to an extended analysis of the Casimir force, with the aim of finding a method for determining the so far unknown average frequency [35] . This can be done at the largest available Casimir force, i.e. that acting between two metal plates with zero spacing and where the electromagnetic skin depth plays the rôle of an equivalent gap between the plates. To avoid microscopic matching of the plate metal structures, different plate metals should be used, also having different electric resistivities. As a result, the Casimir pressure is then obtained as a function of the average frequency, and the shape of this function differs for different metals, thus giving a possibility for determination of the local value of. This would hold, provided that the plate adhering forces remain small as compared to the maximum Casimir force.

3.2. New Fundamental Results of the ZPE Frequency Distribution

The revised ZPE frequency distribution has given rise to a number of new fundamental results as follows:

・ This distribution of photons constitutes a real macroscopic pressure having an application to the large-scale dynamics of the expanding universe [9] [33] [34] . It is thus proposed that the pressure gradient of the ZPE photon gas can play the rôle of an expanding dark energy force, at the same time as the energy density of the same gas plays the rôle of gravitating dark matter and a contracting force. This should in particular apply to the present and later stages of the expanding universe. Being already in the lowest energy state, the ZPE photons do not radiate in a statistical equilibrium of maximum entropy.

・ The coincidence problem concerning equal orders of vacuum energy density and mass density becomes flexible, and does not have to be related to a fixed cosmological constant.

・ The present dynamical model of the expanding universe is reconcilable with the cosmical dimensions and the radius R₀ = 10²⁶ m of the observable universe [9] . This comes out from an average density 10⁻²⁶ kg/m³ of normal matter according to Linde [36] , the mass contents of 21% and 4% of dark and normal matter, and an integrated amount of dark matter having the mass

(21)

due to the present theory where G = 6.673 × 10⁻¹³ m³∙kg⁻¹∙s⁻¹ is the Newtonian constant of gravitation.

・ An observed acceleration of about 4 × 10⁻¹⁰ m/s² at the present stage of expansion can be explained by a dynamic unbalance due to a dominating dark energy of about 75% [9] .

・ The expanding cloud of ZPE photons has at present the character of a nearly flat Euclidian geometry. This is found to be consistent with a stable dynamic state being subject to expansive or compressive perturbations [37] .

・ In a proposed generalized theory of gravitation with both polarities of mass and of mutual forces, a mechanism for separation of matter from antimatter may be provided at an early stage of the expanding universe [7] [38] . This could also reveal itself as a “dark flow” in certain regions.

4. Conclusions

According to both theory and experiments, the vacuum is not a state of empty space but is populated by electromagnetic fluctuations at a lowest nonzero energy level, the Zero Point Energy. This review describes how the ZPE is included in a revised quantum electrodynamical theory (RQED) being applied on the scale of elementary particles. The ZPE also applies to the physics of large-scale cosmical phenomena such as the expanding universe, and in terms of a revised frequency distribution.

The Standard Model of elementary particles, which is based on a vacuum state of empty space, is here replaced by RQED theory. Thereby the ZPE is shown to be represented by a nonzero electric field divergence. This leads to massive elementary particles from the beginning, independently of and distinguished from the theory by Higgs. The basic features of the unstable Higgs-like particle recently detected in the experiments at CERN, such as zero charge, zero spin, and an effective radius of about 10⁻¹⁸ m being consistent with a rest mass of 125 GeV, are also reproduced by RQED theory. The same theory further leads to a number of fundamental results beyond those by Dirac and Higgs, such as a deduced value of the elementary charge positioned in a narrow range close to its experimental value, a confining magnetic field which prevents the charged leptons from “exploding” under the action of their electrostatic eigenforce, large intrinsic and local electric charges of both polarities within the body of a particle configuration, a photon spin being associated with a very small but nonzero photon rest mass, and photon wave packet solutions of a needle-like character which contribute to the understanding of the photoelectric effect and of two-slit experiments.

The real macroscopic pressure due to the revised ZPE frequency distribution should further influence the large-scale dynamics of the expanding universe, in particular at its present and later stages. This concerns the mechanisms of dark energy and dark matter which are proposed to originate from the pressure gradient and mass density of the ZPE photon gas. The resulting theory leads to an explanation of the coincidence problem being independent of the cosmological constant, to an agreement between the deduced and observed scales of the universe, to an accelerated expansion being consistent with observations, and to the stability of such a nearly flat universe. Also a “fine structure” with local variations and concentrations of ZPE dark matter would become imaginable.

The future will indicate what is relevant and not relevant in these efforts and theories.

References