Journal of Electromagnetic Analysis and Applications
Vol.5 No.4(2013), Article ID:29719,7 pages DOI:10.4236/jemaa.2013.54028
Negative Refraction in Chiral Plasma Media
![]()
Escuela de Ingeniería Eléctrica Electrónica, Universidad de Tarapacá, Arica, Chile.
Email: htorres@uta.cl
Copyright © 2013 Héctor Torres-Silva. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 30th, 2013; revised February 28th, 2013; accepted March 15th, 2013
Keywords: Plasma; Negative Refraction; Metamaterial; Chiral Waves
ABSTRACT
Negative refraction is currently achieved by driving the magnetic permeability and electrical permittivity simultaneously negative. It is studied an alternative route to negative refraction without manipulating these parameters ( and
and ) on a chiral magnetized plasma. By adding chirality to the plasma, we obtain windows where the refraction is negative. The size of these windows depends on parameters such as: chirality degree, external magnetic field and the angle of incidence of the electromagnetic wave. The present study demonstrates that the condition for negative phase-velocity propagation can be satisfied by non dissipative Faraday chiral medium such as a very dilute magnetized space plasma.
) on a chiral magnetized plasma. By adding chirality to the plasma, we obtain windows where the refraction is negative. The size of these windows depends on parameters such as: chirality degree, external magnetic field and the angle of incidence of the electromagnetic wave. The present study demonstrates that the condition for negative phase-velocity propagation can be satisfied by non dissipative Faraday chiral medium such as a very dilute magnetized space plasma.
1. Introduction
During the past few years, a new type of artificial metamaterials (called left-handed media or negative refractive index media), whose electric permittivity and magnetic permeability are simultaneously negative in certain frequency bands, attracted considerable attention of many researchers in various fields (see e.g. [1-3]).
Negative refraction is a property of these artificial materials and could in principle be used to construct optical microscopes for imaging as small as molecules, and even to create devices disguised to make objects invisible.
These metamaterials exhibit a number of peculiar electromagnetic and optical effects/phenomena, including reversals of both Doppler shift and Cherenkov radiation [1], negative refraction [1], amplification of evanescent waves, negative Goos-Hanchen shift, reversed circular Bragg phenomenon, and unusual quantum optical effects [1-4].
Very recently, Tretyakov and Pendry et al. demonstrated that the backward wave with negative phase velocity can propagate in chiral materials with nihility [5-7]. This is a new approach to the negatively refracting materials, where the chiral nihility can be achieved at or near the resonant frequency of the permittivity. But the nihility does not arise in the case away of resonance. Moreover, the negative refractive index near resonance of the permittivity will get a large imaginary part. This means that in the scheme of chiral nihility, the realization of the negative refractive index with nearly zero imaginary part near resonance is in general impossible. Obviously, the impact can be enormous if the negative refraction of the chiral materials could be realized in the case of far off resonance of the permittivity.
In the present paper, we consider the backward wave propagation in a gyroelectric chiral medium, in which the negative refraction is no longer limited to the resonance of the permittivity. It can be found that the gyroelectric chiral medium may have an advantage over the chiral medium: specifically, the gyroelectric parameter can dramatically reduce the equivalent permittivity of the eigenmodes, and so the nihility in the equivalent permittivity may be easily achieved in the gyroelectric chiral medium. Thus the negative refraction may be conveniently realized experimentally even far off resonance of the permittivity.
Plasma metamaterials which were recently reported [8,9] have advantages over ordinary metamaterials because a dynamic change of permittivity and tunable amplitude on the complex plane can be manipulated by external power supply for plasma generation and adjustable gas pressure. Now, if the power of the microwave is beyond ignition threshold of microwave plasmas, electron density will be enhanced and lead to additional plasma generation which modifies permittivity in space and the wave propagation itself; this is a feedback phenomenon. Thus, novel schemes are expected to emerge from plasma generation in metamaterial structures.
In previous paper [10,11], we modeled the plasma dispersion relation with waves propagation along and across the external magnetic field. This chiral magnetized plasma corresponds to a gyroelectric chiral medium. In [10,11], we studied and discussed the wave propagation under normal conditions of the dispersion relation, that is propagation waves with positive refraction. Here we review the situation where negative refraction can occur and show that the dispersion relation has some windows or regions where the refraction is negative.
2. Negative Refraction of Magnetized Chiral Plasma
The dispersion relation obtained in [10,11], for electromagnetic waves propagating in a collisionless homogeneous chiral plasma is given by:
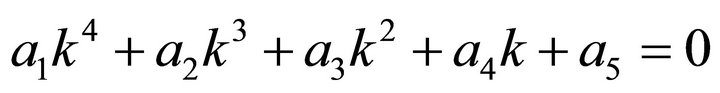 (1)
(1)
where

with the following values of permittivity:
 and
and 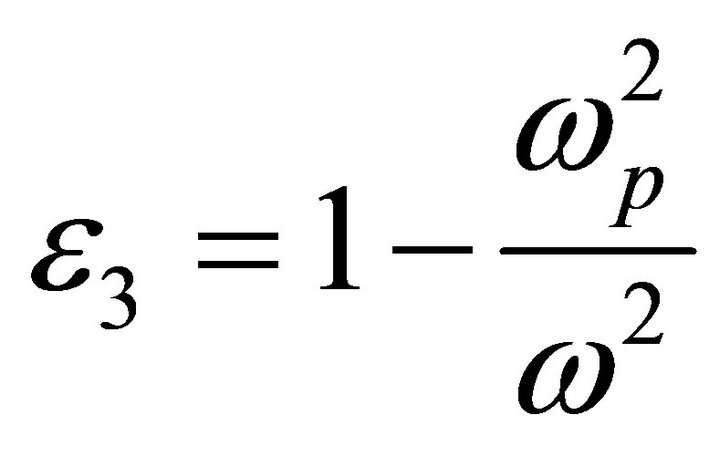
where  is the plasma frequency,
is the plasma frequency,  is the gyrofrequency given by
is the gyrofrequency given by
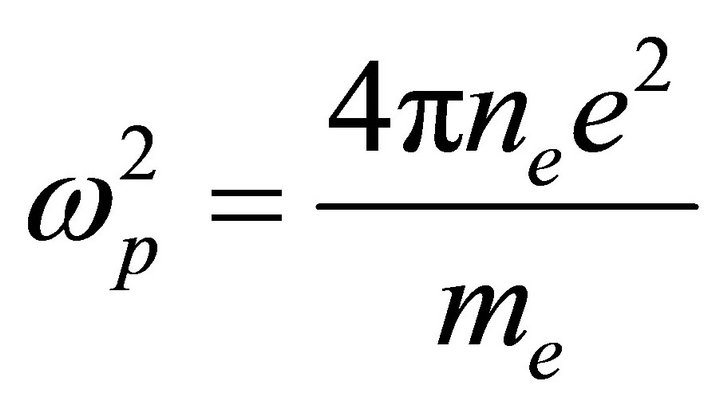 and
and 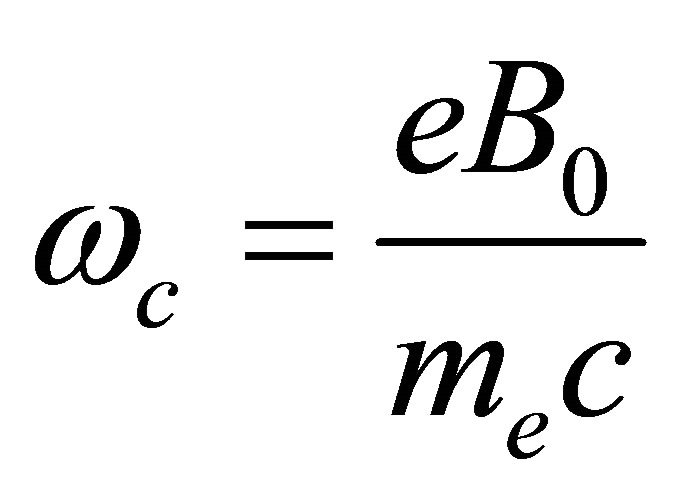
respectively. The chiral parameter is represented by t.
Details of circularly polarized waves, the mode conversion, the combined effects on the Faraday rotation and the chiral behavior of a cold magnetized plasma are described in references [10,11]. There, we show results of the dispersion relation for positive refraction. In this work we study the case of negative refraction, which is obtained when the group velocity, 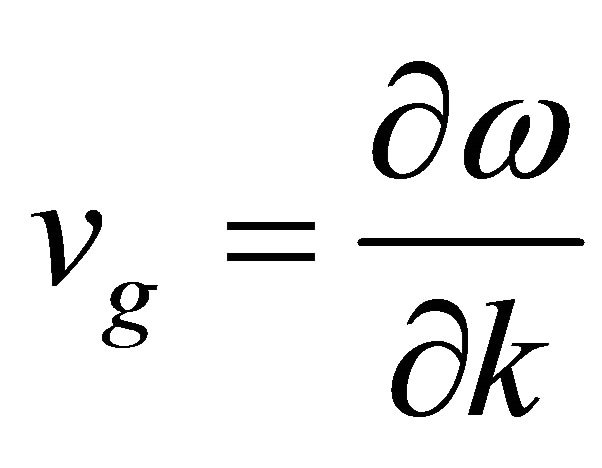 has the opposite sign to the phase velocity,
has the opposite sign to the phase velocity, 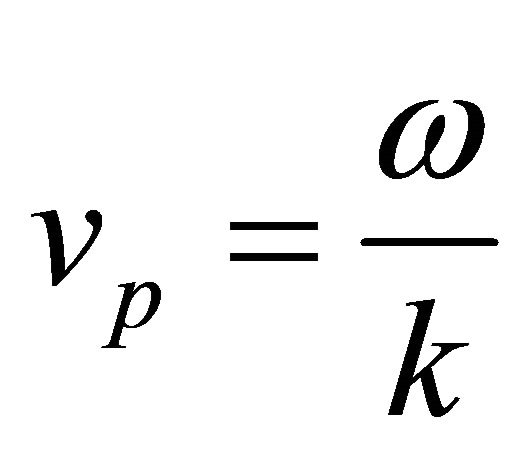 , but only for one polarization. This means that the phase velocity is anti parallel to the vector
, but only for one polarization. This means that the phase velocity is anti parallel to the vector . This is the signature of negative refraction.
. This is the signature of negative refraction.
Since Equation (1) has four roots, there exist four eigen modes (including the counterpropagating modes and their respective mutually perpendicular polarization components) corresponding to a monomode frequency ω. Here we point out that the coefficients  and
and  have explicit physical meanings, which correspond to some nontrivial effects. For example, the nonzero coefficient
have explicit physical meanings, which correspond to some nontrivial effects. For example, the nonzero coefficient  in Equation (1) will inevitably lead to a non-degenerate |k| (and hence a possibility of backward wave propagation and negative refraction in the anisotropic material).
in Equation (1) will inevitably lead to a non-degenerate |k| (and hence a possibility of backward wave propagation and negative refraction in the anisotropic material).
In our case 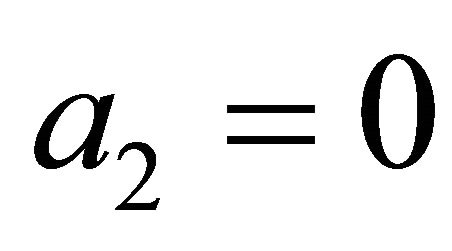 but can appear if quantum effects are take into account.
but can appear if quantum effects are take into account.
The dispersion relation 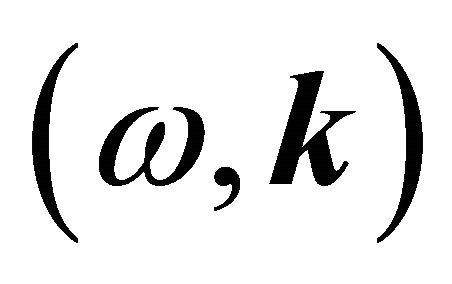 given by Equation (1) is plotted in Figure 1, with the following considerations:
given by Equation (1) is plotted in Figure 1, with the following considerations:  and
and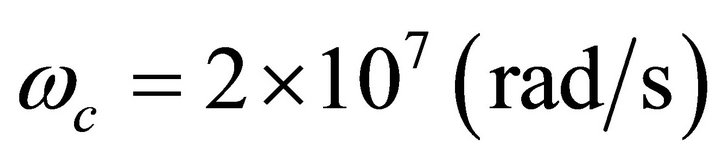 . The solid curves are without chirality
. The solid curves are without chirality 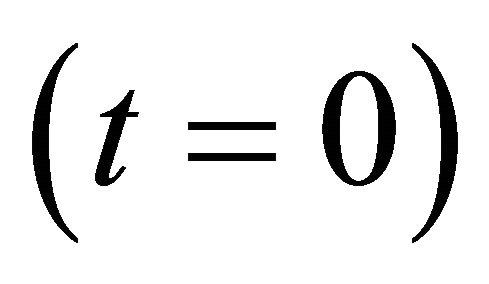 and the dashed curves are with
and the dashed curves are with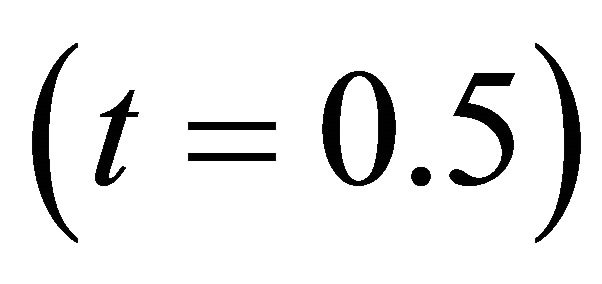 . Figure 1 shows the dispersion relation for these two scenarios. Upper solid curve corresponds to the right circularly polarized wave.
. Figure 1 shows the dispersion relation for these two scenarios. Upper solid curve corresponds to the right circularly polarized wave.
Plasma media without chirality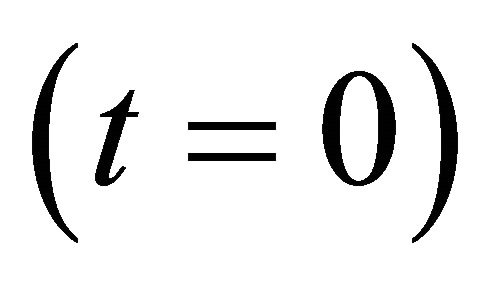 , gives a dispersion relation with even symmetry because the Equation (1) is reduced to
, gives a dispersion relation with even symmetry because the Equation (1) is reduced to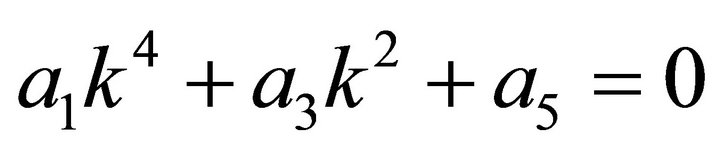 . Here, we can analyze the phase velocity and the group velocity in this magnetized cold plasma.
. Here, we can analyze the phase velocity and the group velocity in this magnetized cold plasma.
For  and
and 
 and
and 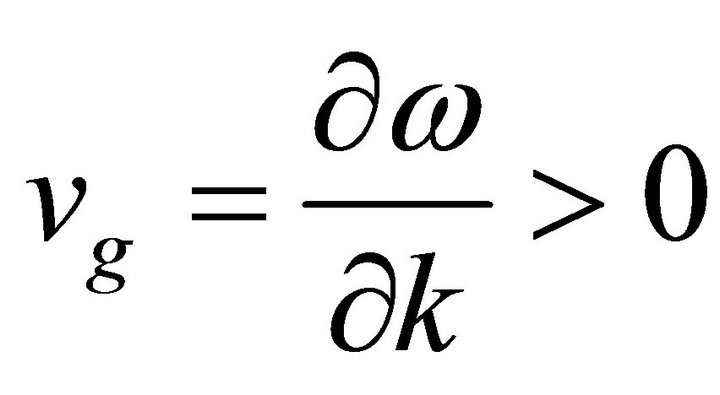
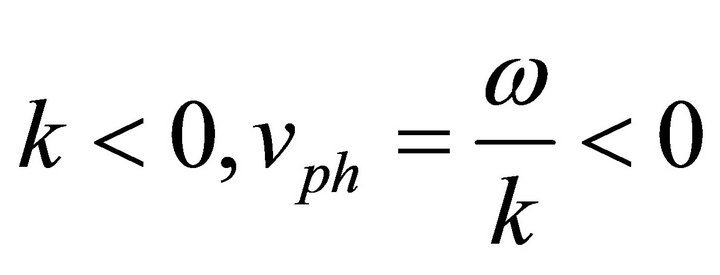 and
and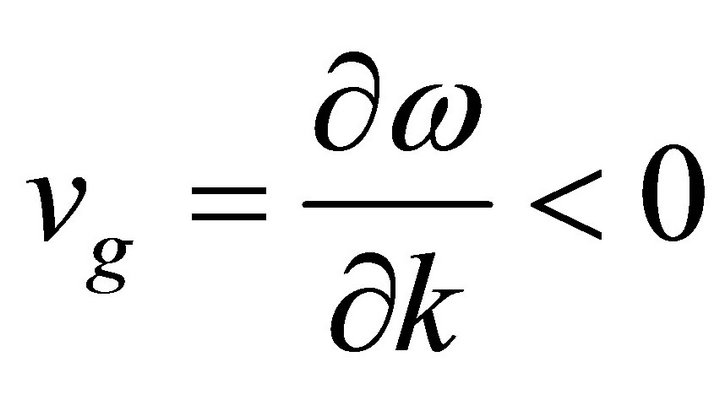 .
.
In both cases we find that the phase velocities and group have the same sign, which confirms that this plasma corresponds to conventional cold plasma and there is no negative refractive index [12]. This means that the backward wave propagation and negative refraction cannot arise in gyrotropic (gyroelectric and gyromagnetic) materials.
When chirality is introduced into the media , there is a break of symmetry and the function of dispersion is rotated and shifted as shown in Figure 1. Unlike the previous case, the group velocity can have the opposite sign to the phase velocity, so there are regions of
, there is a break of symmetry and the function of dispersion is rotated and shifted as shown in Figure 1. Unlike the previous case, the group velocity can have the opposite sign to the phase velocity, so there are regions of where negative refraction is obtained.
where negative refraction is obtained.
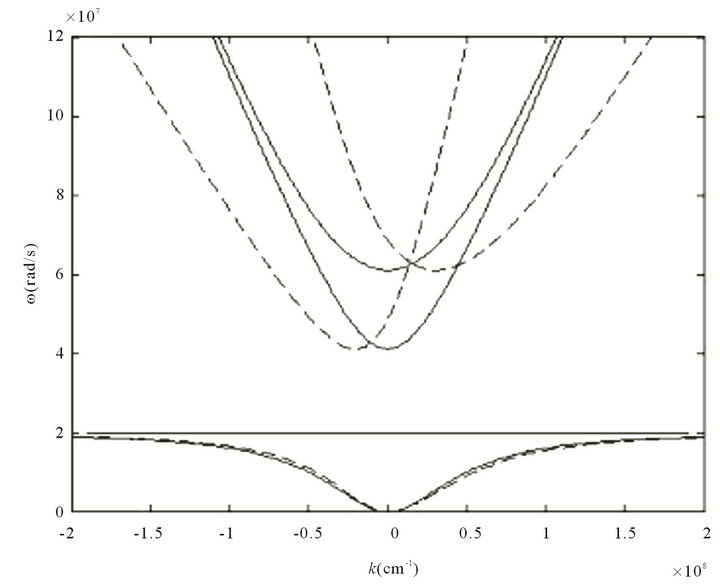
Figure 1. Dispersion relations for plasma media with and without chirality. Solid curves correspond to t = 0. Dashed curves correspond to t = 0.5. Here we reproduce the results obtained in [10,11].
In Figures 2 and 3, we show two regions or windows of the dispersion relation with negative refraction like a metamaterial:
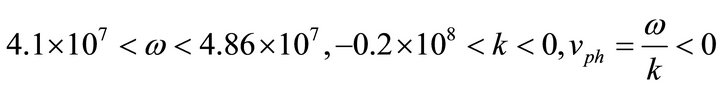
and
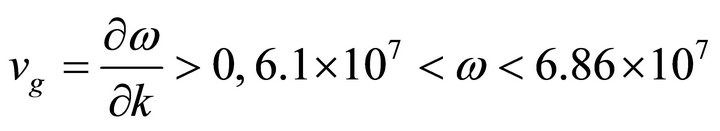
and
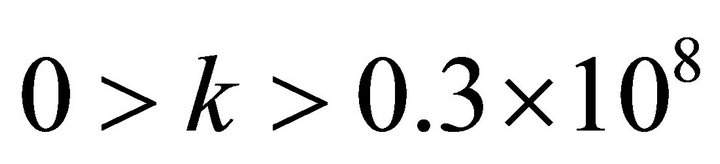
the 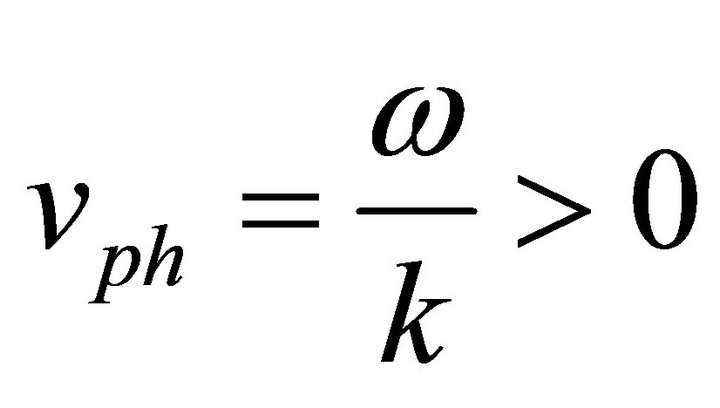 and
and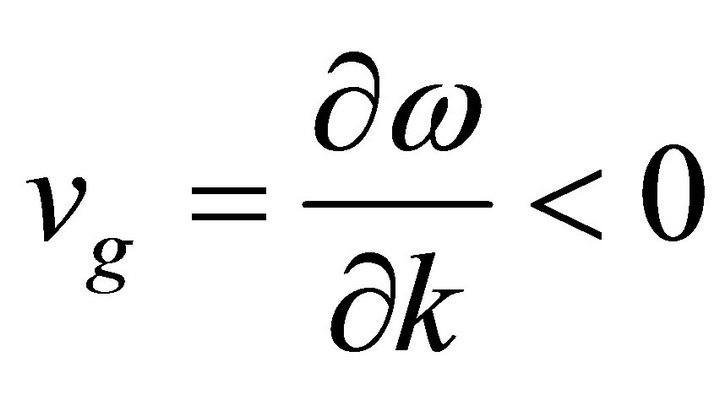 .
.
As can be seen, through the chirality, negative refraction property is obtained in a plasma medium without manipulation of electric permittivity and magnetic permeability. Figures 2 and 3 plot the range of interest for different values of chirality t.
From the previous graphs, we can discern that there is some control over the negative refraction through the chirality factor. This is a new route to realize the negative refraction. The permittivity and permeability in this scenario can be positive when the backward wave propagation is realized. This is a feature that is quite different from the previous schemes such as artificial metamaterials [1-6], where only when the permittivity and permeability of the material are simultaneously negative can the negative refractive index be achieved.
The plasma is exposed to a magnetic field 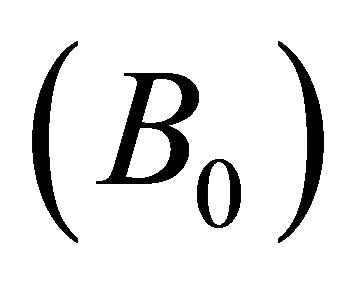 directly related to the gyrofrequency
directly related to the gyrofrequency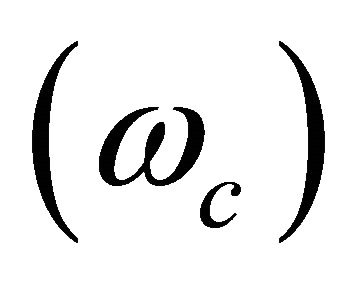 . Figure 4 is plotted the dispersion relation for different values of
. Figure 4 is plotted the dispersion relation for different values of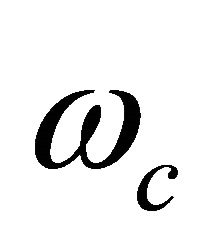 . As shown in this figure, increasing the magnetic field
. As shown in this figure, increasing the magnetic field  in chiral plasma contracts the region where it acts as a left-handed medium.
in chiral plasma contracts the region where it acts as a left-handed medium.
With this non dissipative example, we have shown that an incident plane wave with positive phase velocity can result in a negatively reflected plane wave with negative phase velocity, as well as a positively reflected planewave with positive phase velocity. Also, an incident plane wave with negative phase velocity can result in a negatively reflected plane wave with positive phase velocity, as well as a positively reflected plane wave with negative phase velocity. Thus, negative reflection is characterized by a reversal in the co/contra directionality of the wave vector and the time-averaged Poynting vector.
Clearly,  is the optimal case for the propagation of electromagnetic waves. Figure 5 shows the dispersion relation of chiral plasma media
is the optimal case for the propagation of electromagnetic waves. Figure 5 shows the dispersion relation of chiral plasma media  in which waves with different incidence angles.
in which waves with different incidence angles.
Figure 5 shows that increasing the angle of incidence of electromagnetic waves, greatly reduces the range where negative refraction exists.
These results can be important to model and to set limits to the difference in velocity between right and left circulary-polarized waves in interstellar and intergalactic space due to effects other than de Faraday rotation [13].
As application of this study, one may envisage relativistic negative refraction being exploited in astronomical scenarios such as, for example, in the remote sensing of planetary and asteroidal surfaces from space stations. Although current research activities relating to negative refraction are largely directed towards the nanoscale, it may possibly be the case that space telemetry technolo-
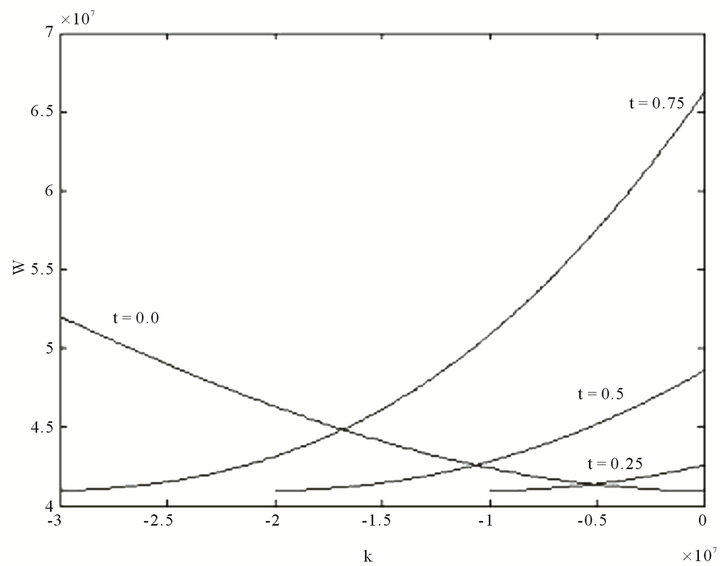
Figure 2. Dispersion relations for different values of chirality t = 0, 0.25, 0.5, 0.75 with .
.
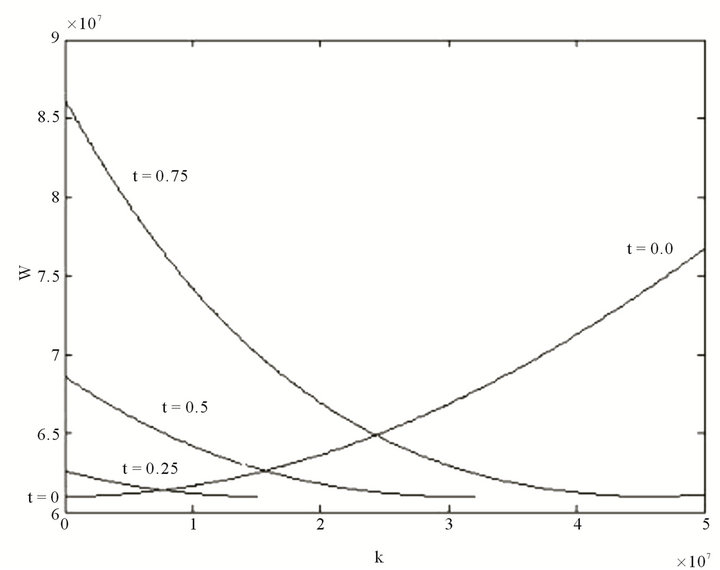
Figure 3. Dispersion relations for different values of chirality t = 0, 0.25, 0.5, 0.75 with .
.

Figure 4. Left-handed medium range for different values of .
.
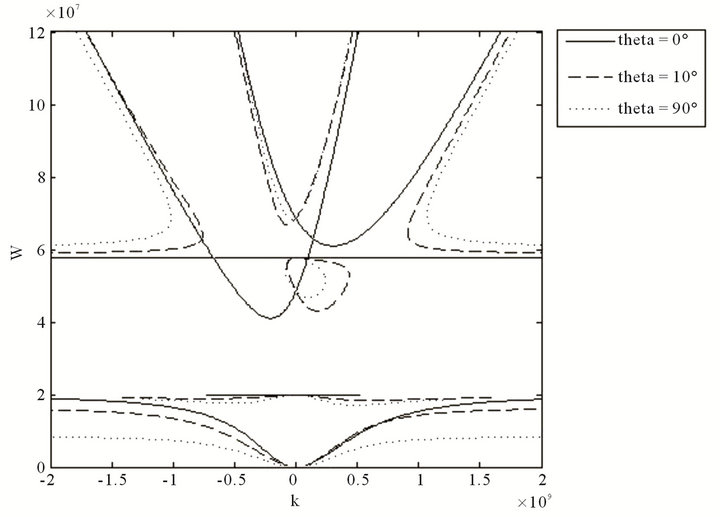
Figure 5. Dispersion relation of a chiral plasma medium in which waves affect different angles.
gies will be the first to reap the benefits of negative refraction. Furthermore, it is possible that many unusual effects would be discovered and/or explained by the application of the idea of negative refraction to interpret data collected via telescopes, i.e., constraints on pseudo photon interaction from CMB polarization observation, new results on Faraday rotation of microwave background polarization and new measurements of cosmological lepton asymmetry. Perhaps, many more planets, hitherto hidden, would be lit up on our space maps thereby [13-16]. In this context, the coefficient 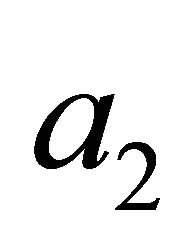 can have a physical meaning related to the summation of the wave numbers over the four eigen modes, and so a nonzero value of
can have a physical meaning related to the summation of the wave numbers over the four eigen modes, and so a nonzero value of 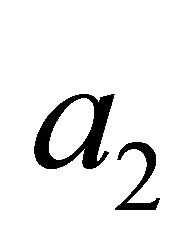 means a breaking of the universal symmetry in the quantum-vacuum eigen modes inside the material like a magnetized star. For example, the quantumvacuum fluctuation field in such an anisotropic electromagnetic material would have a nonzero electromagnetic angular momentum (since the universal symmetry of the vacuum is broken) and hence the non compensation effect of the vacuum eigen modes (the forward and backward wave modes as well as their respective leftand right-handed polarization components) in the anisotropic material arises. It is thus possible for the angular momentum transfer between the anisotropic electromagnetic medium and the quantum vacuum to take place. The coefficient
means a breaking of the universal symmetry in the quantum-vacuum eigen modes inside the material like a magnetized star. For example, the quantumvacuum fluctuation field in such an anisotropic electromagnetic material would have a nonzero electromagnetic angular momentum (since the universal symmetry of the vacuum is broken) and hence the non compensation effect of the vacuum eigen modes (the forward and backward wave modes as well as their respective leftand right-handed polarization components) in the anisotropic material arises. It is thus possible for the angular momentum transfer between the anisotropic electromagnetic medium and the quantum vacuum to take place. The coefficient 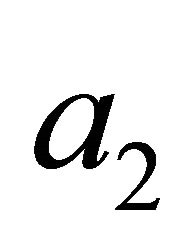 can appear if we study the chiral magnetized plasma with the constitutive relation of the form considered in [17,18] that is with the time variation as
can appear if we study the chiral magnetized plasma with the constitutive relation of the form considered in [17,18] that is with the time variation as . In a future work, we hope to study these phenomena.
. In a future work, we hope to study these phenomena.
3. Conclusions
We have theoretically and numerically examined the propagation of electromagnetic plane waves with the time-averaged Poynting vector directed in opposition to the wavevector. Chiral plasma media offer an alternative route for negative refraction without manipulation of the electric permittivity and magnetic permeability.
There is some control against the size of the window of frequencies where there is negative refraction is dependent on some variables such as: Chirality degree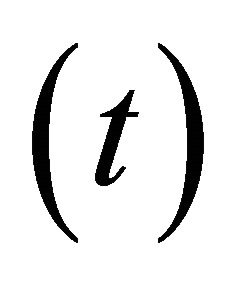 , the angle of incidence of electromagnetic wave
, the angle of incidence of electromagnetic wave 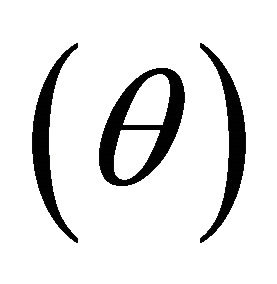 and the magnetic field strength
and the magnetic field strength 
With proper driving of any of these 3 variables can be done to increase the range of frequencies where refraction is negative.
By increasing the degree of chirality of plasma results in a greater range metamaterial, as well as to minimize the angle of incidence of the wave on the plasma medium or even reducing the magnetic field which means choosing frequencies that meet the following relationship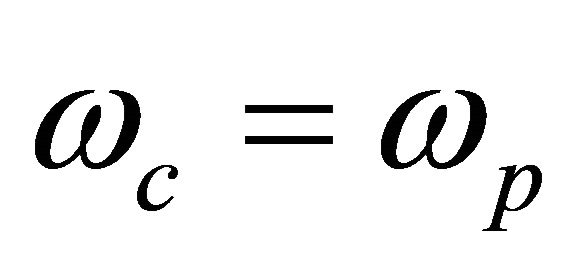 . The present study demonstrates that the condition for negative phase-velocity propagation can be satisfied by non dissipative Faraday chiral medium with constitutive scalar that are all positives. In this form, we show that this scheme offers an alternative route to negative refraction without manipulating the effective permitivity and permeability of the medium.
. The present study demonstrates that the condition for negative phase-velocity propagation can be satisfied by non dissipative Faraday chiral medium with constitutive scalar that are all positives. In this form, we show that this scheme offers an alternative route to negative refraction without manipulating the effective permitivity and permeability of the medium.
The implications of negative refraction propagation may facilitate the search for dark matter in the Universe and may shed light on other poorly understood phenomena such as the Pioneer 10.
One of the important application fields of electromagnetic waves in space is information carrier in communication between spacecrafts and the base on the earth. One of the crucial problems in this area is blackout in spacecrafts reentering the earth atmosphere [19]. When a spacecraft reenters the earth atmosphere, its kinetic energy loses through friction against low-pressure air gases, and plasma is created beyond the threshold condition determined by the energy balance and the air pressure. The parameters of plasma surrounding a spacecraft depend on specific conditions such as the outer shape of the spacecraft and reentering speed. One report indicates that electron density is on the order of , and the corresponding plasma frequency which is also the wave cutoff frequency is at the low microwave range. That is, if we set a negative-
, and the corresponding plasma frequency which is also the wave cutoff frequency is at the low microwave range. That is, if we set a negative- material on or just beneath the surface of the space craft, low frequency microwaves can penetrate through the plasma region with negative
material on or just beneath the surface of the space craft, low frequency microwaves can penetrate through the plasma region with negative 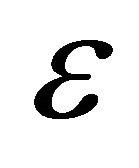 since the refraction index N becomes real and negative [19,20].
since the refraction index N becomes real and negative [19,20].
4. Acknowledgements
This work has been supported by the project No 8731-13 of the Universidad de Tarapacá, Chile. The numerical results were obtained by P. Espinosa (Doctoral Thesis student).
REFERENCES
- V. G. Veselago, “The Electrodynamics of Substances with Simultaneously Negative Values of ε and μ,” Soviet Physics Uspekhi, Vol. 10, No. 4, 1968, pp. 509-514. doi:10.1070/PU1968v010n04ABEH003699
- R. A. Shelby, D. R. Smith and S. Schultz, “Experimental Verification of a Negative Index of Refraction,” Science, Vol. 292, No. 5514, 2001, pp. 77-79. doi:10.1126/science.1058847
- J. B. Pendry, D. Schurig and D. R. Smith, “Controlling Electromagnetic Fields,” Science, Vol. 312, No. 5781, 2006, pp. 1780-1782. doi:10.1126/science.1125907
- A. Lakhtakia and T. G. Mackay, “Fresnel Coefficients for a Permittivity-Permeability Phase Space Encompassing Vacuum, Anti-Vacuum, and Nihility,” Microwave and Optical Technology Letters, Vol. 48, No. 2, 2006, pp. 265-270. doi:10.1002/mop.21323
- S. Tretyakov, I. Nefedov, A. Sihvola, S. Maslovski and C. Simovski, “Waves and Energy in Chiral Nihility,” Journal of Electromagnetic Waves and Applications, Vol. 17, No. 5, 2003, pp. 695-706. doi:10.1163/156939303322226356
- J. Pendry, “A Chiral Route to Negative Refraction,” Science, Vol. 306, No. 5700, 2004, pp. 1353-1355. doi:10.1126/science.1104467
- T. G. Mackay, “Erratum: Plane Waves with Negative Phase Velocity in Isotropic Chiral Mediums,” Microwave and Optical Technology Letters, Vol. 47, No. 4, 2005, p. 406. doi:10.1002/mop.21183
- O. Sakai, T. Naito, T. Shimomura and K. Tachibana, “Microplasma Array with Metamaterial Effects,” Thin Solid Films, Vol. 518, No. 13, 2010, pp. 3444-3448. doi:10.1016/j.tsf.2009.11.040
- O. Sakai, T. Shimomura and K. Tachibana, “Negative Refractive Index Designed in a Periodic Composite of Lossy Microplasmas and Microresonators,” Physics of Plasmas, Vol. 17, No. 12, 2010, Article ID: 123504. doi:10.1063/1.3524561
- H. Torres-Silva, et al., “Electromagnetic Properties of a Chiral-Plasma Medium,” Pramana Journal of Physics, Vol. 49, No. 4, 1997, pp. 431-442. doi:10.1007/BF02847430
- H. Torres-Silva, et al., “Electromagnetic Waves in a ChiralPlasma Media,” Journal of the Physical Society of Japan, Vol. 67, No. 3, 1998, pp. 850-857. doi:10.1143/JPSJ.67.850
- T. H. Stix, “The Theory of Plasma Waves,” McGraw-Hill, New York, 1962.
- M. Goldhaber and V. Trimble, “Limits on the Chirality of Interstellar and Intergalactic Space,” Journal of Astrophysics and Astronomy, Vol. 17, No. 12, 1996, pp. 17-21. doi:10.1007/BF02709342
- A. Feigel, “Quantum Vacuum Contribution to the Momentum of Dielectric Media,” Physical Review Letters, Vol. 92, No. 2, 2004, Article ID: 020404. doi:10.1103/PhysRevLett.92.020404
- W. Kinney and A. Riotto, “Measuring the Cosmological Lepton Asymmetry through the Cosmic Microwave Background Anisotropy,” Physical Review Letters, Vol. 83, 1999, pp. 3366-3369. doi:10.1103/PhysRevLett.83.3366
- C. Contalbi, J. Magueijo and L. Smolin, “Anomalous CMB Polarization and Gravitational Chirality,” Physical Review Letters, Vol. 101, 2008, Article ID: 141101.
- H. Torres-Silva and D. Torres C, “Chiral Current in a Graphene Battery,” Journal of Electromagnetic Analysis and Applications, Vol. 4, No. 10, 2012, pp. 426-431.
- H. Torres-Silva and D. T. Cabezas, “Chiral Seismic Attenuation with Acoustic Metamaterials,” Journal of Electromagnetics Analysis and Applications, 2013, in Press.
- O. Sakai and K. Tachibana, “Plasma as Metamaterial: A Review,” Plasma Sources Science and Technology, Vol. 21, No. 1, 2012, pp. 1-18. doi:10.1088/0963-0252/21/1/013001

