Journal of Electromagnetic Analysis and Applications
Vol. 1 No. 4 (2009) , Article ID: 1117 , 5 pages DOI:10.4236/jemaa.2009.14036
Active Power Filter Based on Adaptive Detecting Approach of Harmonic Currents
![]()
School of Electrial Engineering, Beijing Jiaotong University, Beijing, China.
Email: 08122036@bjtu.edu.cn, yptang@bjtu.edu.cn
Received September 17th, 2009; revised October 29th, 2009; accepted November 7th, 2009.
Keywords: Adaptive Interference Canceling, Adaptive Harmonic Detecting, Active Power Filter
ABSTRACT
The ip-iq detection method based on instantaneous inactive power theory has been applied widely in active power filter because of its good real-time. But it needs large computation, and three-phase currents are processed as integrity, thus calculation accuracy can't be ensured. Based on adaptive interference canceling theory, this paper presents a new adaptive detection method for harmonic current, it is a continuously regulated closed-loop system, and its operating characteristics are almost independent of the parameter variations of the elements, thus it performs better than that based on traditional theory. At last this paper provides the simulation of active power filter including the detecting circuit which proved the design is feasible and correct.
1. Introduction
Because of the use of more nonlinear loads, especially more power electronic equipments, a large number of harmonic and reactive currents have been introduced into power grid, resulting in some problems such as voltage flicker, frequency variation, imbalance of three-phase problem, etc [1]. In order to suppress the harmonics, passive filters have been used in the past years [2], while recently Active Power Filter (APF) has been developed rapidly. Widely used in APF, the harmonic detection method is based on three-phase instantaneous inactive power theory. Thus a lot of analog multipliers and calculation are needed, resulting in difficult adjust and poor performance [3-4]. Furthermore, this method is only suitable for a three-phase equilibrium sinusoidal system.
This paper presents a new adaptive closed-loop detection method based on adaptive interference canceling theory, and the simulation results show that the filter based on this new method performs better than that based on the three-phase instantaneous inactive power theory, and with higher accuracy [5].
2. The Basic Principle of an Active Filter
An active power filter is a new power electronic device of dynamic harmonic suppression. Figure 1 shows the basic principle. There are four parts in a shunt APF: the main circuit, command current operational circuit, current tracking control circuit, and the drive circuit. The command current operation circuit detects the harmonic component iLh, in the load current iL, and takes the opposite value as command signal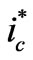 . The principle can be expressed by the following formula
. The principle can be expressed by the following formula
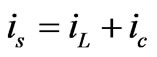
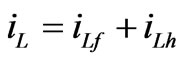
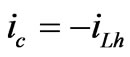
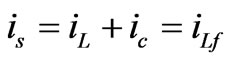
where iS, iL are currents of the supply and a nonlinear load, respectively, and ic is the compensation current. iLf, iLh are the fundamental active and harmonic reactive components of the load current, respectively.
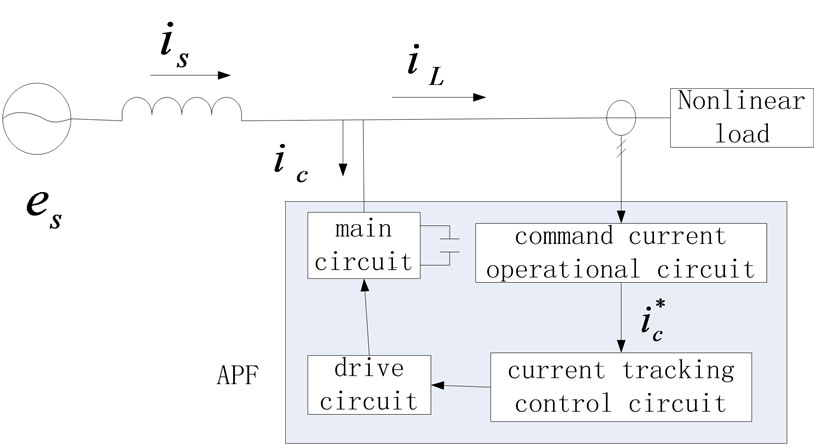
Figure 1. Basic principle block diagram of an active filter
3. Adaptive Detecting Algorithm
3.1 The Basic Principle of Adaptive Interference Canceling Theory
The adaptive interference canceling technique has been widely used in recent years [6]. By continuously selfstudying and self-adjusting, the detecting system can always operate at its best. The basic noise-canceling theory can be illustrated in Figure 2. In the detecting system, there are two unrelated input signals: original input s+n0 and reference input n1. And s is unrelated with n0 and n1, while n0 and n1 are related. The reference input signal n1 is filtered by an adaptive filter to produce an output signal , which is an approximate replica of n0. This output
, which is an approximate replica of n0. This output  is subtracted from the original input signal s+n0 to produce
is subtracted from the original input signal s+n0 to produce , the system output signal.
, the system output signal.
In the system shown in Figure 2, the reference input is processed by an adaptive filter which automatically adjusts its own response through a least-squares algorithm. Thus the filter can detect the noise n0 continuously and adjust the system to minimize the error signal e. It can be proved that 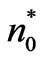 is the best least-squares estimate of n0, when the filter is adjusted to make the error signal power
is the best least-squares estimate of n0, when the filter is adjusted to make the error signal power 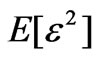 minimum.
minimum.
3.2 Adaptive Harmonic Detection
Based on the principle of adaptive noise canceling theory, adaptive harmonic current detecting circuit is shown in Figure 3. The system is composed of an analog adaptive filter, a BPF (Band Pass Filter) and a 900 phase-shifter [7]. The primary input is the load current: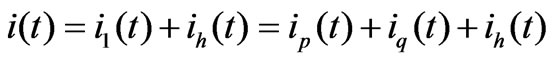 , where i1(t) is the fundamental current, ih(t) is the sum of all harmonic components, and ip(t), iq(t) are the active component and the reactive component of i1(t), respectively in Figure 3. u(t) and u1(t) are the AC source voltage and its fundamental component, respectively. R1(t) and R2(t) are two reference inputs orthogonal to each other, and i0(t) is the system output.
, where i1(t) is the fundamental current, ih(t) is the sum of all harmonic components, and ip(t), iq(t) are the active component and the reactive component of i1(t), respectively in Figure 3. u(t) and u1(t) are the AC source voltage and its fundamental component, respectively. R1(t) and R2(t) are two reference inputs orthogonal to each other, and i0(t) is the system output.
As shown in Figure 3, because both feedback branches are similar, we take the lower feedback branch as an example. Only the fundamental reactive component which has the same frequency with  can produce the DC signal after the output current i0(t) is multiplied by
can produce the DC signal after the output current i0(t) is multiplied by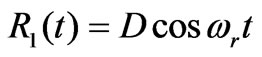 , while other components produce AC signals after the same procession. The DC component can be integrated to get the average value of fundamental reactive current IFp, while the AC component will be zero after the same calculation. Thus, we can get the instantaneous fundamental reactive current ifq(t) by
, while other components produce AC signals after the same procession. The DC component can be integrated to get the average value of fundamental reactive current IFp, while the AC component will be zero after the same calculation. Thus, we can get the instantaneous fundamental reactive current ifq(t) by

Figure 2. Adaptive noise canceling theory
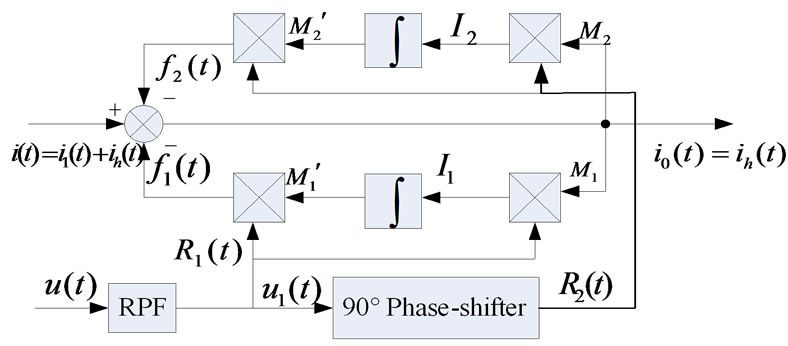
Figure 3. Adaptive detecting diagram for harmonic currents
multiply IFp with R1(t). Similarly, using R2(t), we can get the instantaneous fundamental active current ifp(t). At last, by adding the reverse of ifp(t)+ifq(t) to i(t), the output current i0(t)=ih(t) is produced. If only the current i0(t)=ih(t)+ifq(t) is needed, what we should do is remove the R1(t) branch.
We can also explain the principle in the phase space. Assume the reference inputs which processed by the BPF are:
 ,
,
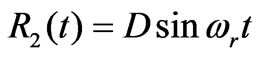 .
.
Then the output of the multiplier M1 can be expressed as:

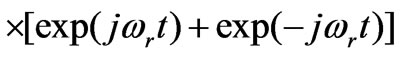 (1)
(1)
Taking the Laplace transform of (1), we have
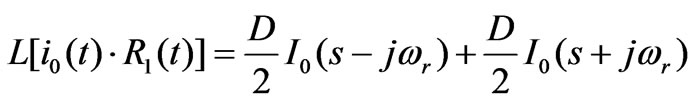 (2)
(2)
where, I0(s) is the Laplace transform of i0(t). After processed by the integrator, whose transform is 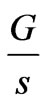 (here G is the integration gain), the transform of the feedback signal can be expressed as:
(here G is the integration gain), the transform of the feedback signal can be expressed as:
 (3)
(3)
The output of the multiplier 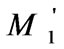 is simply the feedback signal of the lower branch, which mean
is simply the feedback signal of the lower branch, which mean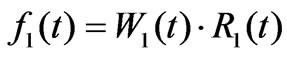 . Its transform is:
. Its transform is:
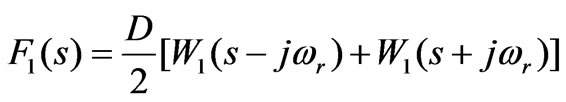
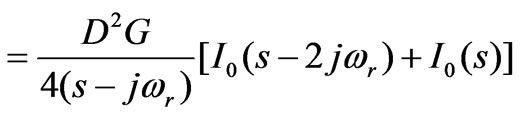
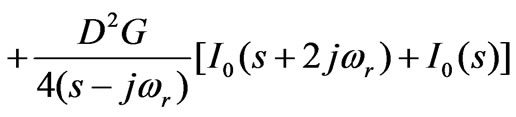
 (4)
(4)
Similarly, the transform F2(s) of the feedback signal f2(t) for the upper feedback branch can be expressed as:

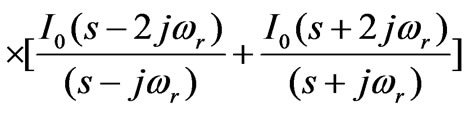 (5)
(5)
The total feedback signal is:
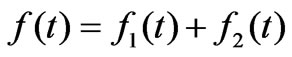
Its transform is:
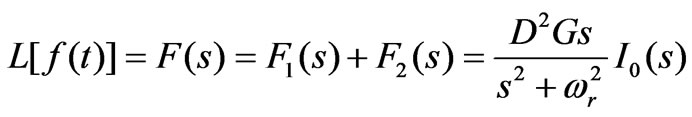 (6)
(6)
Thus the feedback coefficient of the whole system is:
 (7)
(7)
Then the transfer function H(s) of the system is:
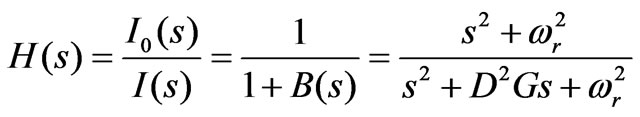 (8)
(8)
From (8), when ,
, 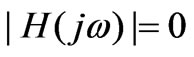 , which means a zero point exists in the system corresponding to the fundamental frequency
, which means a zero point exists in the system corresponding to the fundamental frequency 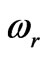 Consequently the fundametal signal will be greatly attenuated. It is obvious that the system shown in Figure 3 is equivalent to an ideal second-order notch filter. In addition, the center frequency of the system depends solely on the frequency signal
Consequently the fundametal signal will be greatly attenuated. It is obvious that the system shown in Figure 3 is equivalent to an ideal second-order notch filter. In addition, the center frequency of the system depends solely on the frequency signal  of the reference input. Therefore, the system is independent of parameter of the circuit components, which means that the system is almost stable while the temperature varies or the circuit components ages.
of the reference input. Therefore, the system is independent of parameter of the circuit components, which means that the system is almost stable while the temperature varies or the circuit components ages.
3.3 DC Side Voltage Control
Ideally, what an active filter compensates is the non-active power; that is to say, it neither absorbs active power from the power supply nor outputs to it, so the DC side voltage of an active filter is constant. However, due to the loss of the active filter, energy in the capacitor on
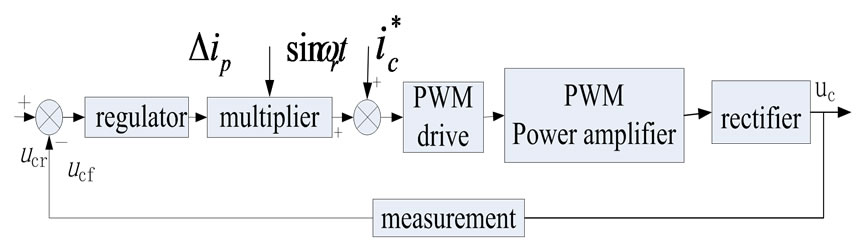
Figure 4. DC voltage control block diagram
the DC side will reduce, making the voltage on the capacitor drop.
In order to maintain the voltage on the capacitor, the feedback method has usually been adopted, whose purpose is to obtain some active power from the source to compensate the corresponding loss.
As shown in Figure 4, Ucr , Ucf are the reference and feedback values of Uc, respectively. The difference between Ucr and Ucf is regulated by PI to get the signal .
.
Since 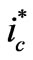 contains the fundamental active component , ic, which comes from
contains the fundamental active component , ic, which comes from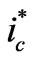 , also contains such a component. Therefore, when ic is introduced into the power system, APF can exchange the active energy between AC and DC sides, which keeps Uc constant.
, also contains such a component. Therefore, when ic is introduced into the power system, APF can exchange the active energy between AC and DC sides, which keeps Uc constant.
4. Simulation Results
In this section, computer simulation is carried out to verify the design of the adaptive shunt active filter. A three-phase distribution system is built using Matlab as shown in Figure 5. Simulation parameters are as following: AC source is 220V/50Hz, supply side inductance Ls is 0.2μH. The nonlinear load parameters for three-phase full-controlled bridge rectifier are R= 20Ω, L=0.1H. In the main circuit of the active filter, IGBT is used as the switch, and the inductance on the AC side La is 5mH, while the capacitance is 2200μF/1000V on the DC side.
Figure 6 shows the AC source voltage, the power supply currents before and after filterd, respectively, and the harmonic and reactive reference currents. From Figure 6(b), we can see that before filtered, the current lags the source voltage and contains a lot of harmonic and reactive components. After filtered by the APF, shown in Figure 6(d), the supply current is nearly sinusoidal and in phase with AC source voltage, which means APF corrects the power factor of the supply side nearly to unity. There is a variation in the nonlinear current at t=0.1s, From Figure 6 it can be seen the proposed adaptive shunt active filter only needs approximately half a cycle to adapt itself to the change.
Since the APF adopts traditional hysteresis current control method, the tracking ability of APF is limited, resulting in some ripples in the current when it changes suddenly, as shown in Figure 6(d).
The DC capacitor voltage is shown in Figure 7, it only

Figure 5. Active filter simulation model
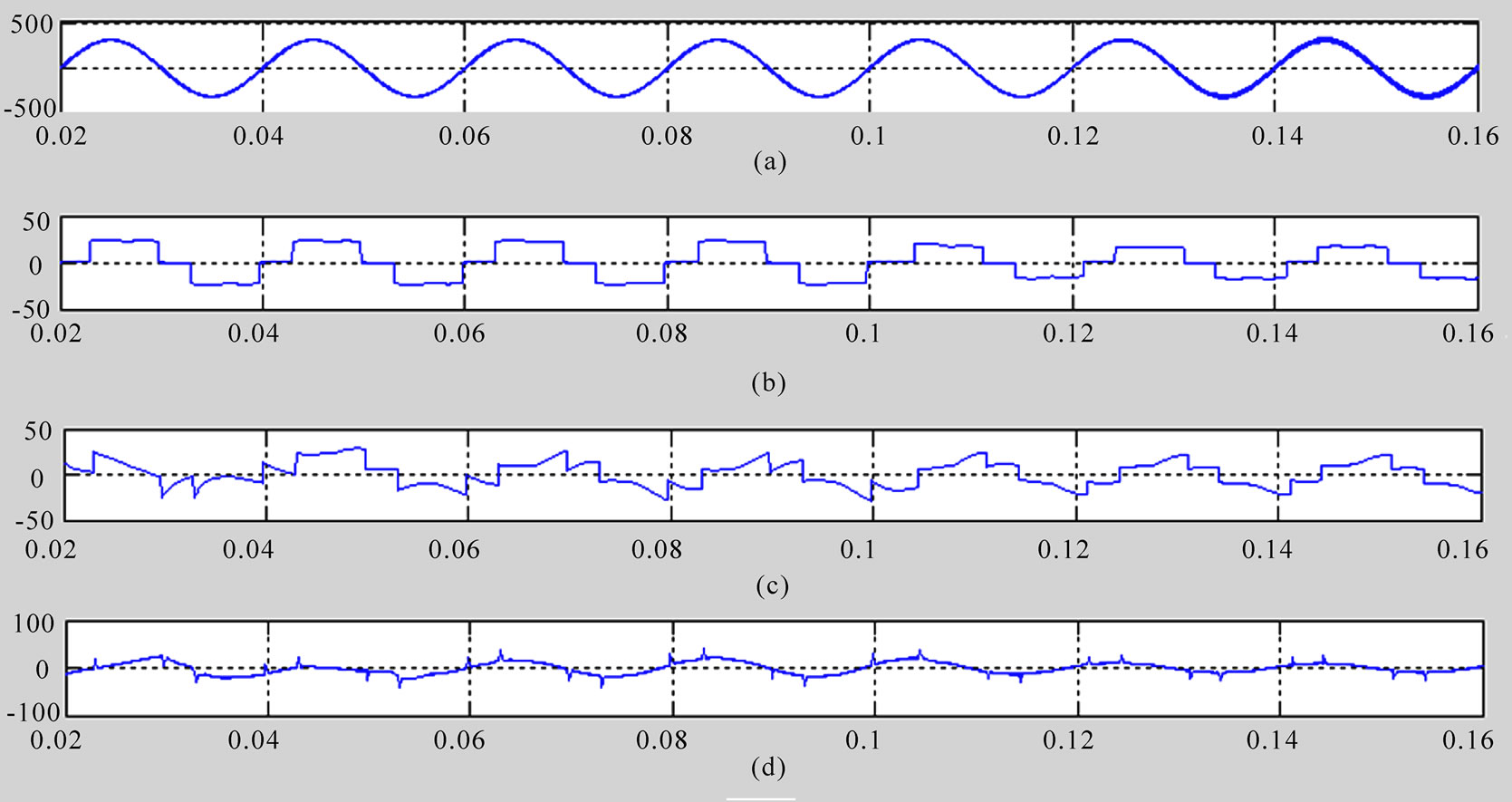
Figure 6. Simulation result of detection for harmonic and reactive currents. (a) ac source voltage for phase A, (b) power supply currents for phase A before filter input, (c) harmonic and reactive reference current from adaptive detection, (d) power supply currents for phase A after filter input

Figure 7. DC side capacitor voltage of active filter
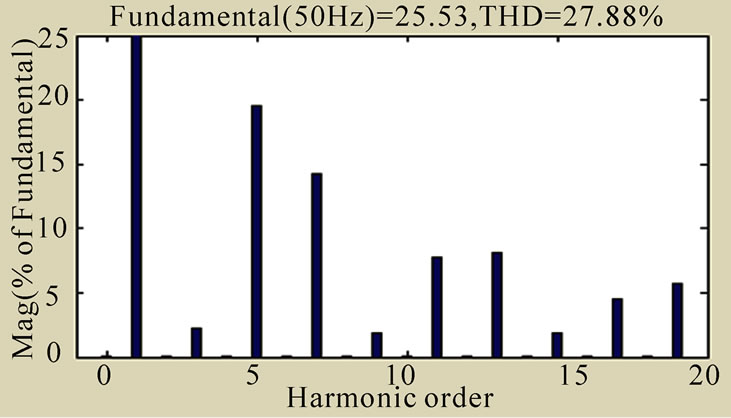
Figure 8. FFT analysis of the supply current before APF input

Figure 9. FFT analysis of the supply current after APF input based on adaptive interference canceling theory

Figure 10. FFT analysis of the supply current after APF input based on instantaneous inactive power theory
takes about 0.05s to reach at the desired value of 1000V and stabilize rapidly.
Compared Figure 8 with Figure 9, it shows the harmonic and reactive currents are greatly restrained.
It shows from Figure 9 and Figure 10, under the same conditions, after APF input, the THD of the supply current based on adaptive interference canceling theory drops to 10.50%, but that based on instantaneous inactive power theory is only 12.30%, moreover, the method based on traditional theory uses 6 analog summer, 4 multipliers and lots of gains, thus the calculation accuracy is more difficult to be assured in practice. The method based on adaptive interference canceling theory uses only 6 multipliers and 3 integrators, which ensures better performance in actual operation than that based on instantaneous inactive power theory.
Overall, it shows that the proposed adaptive shunt active filter can compensate nonlinear load current, adapt itself to compensate the variations in nonlinear load currents and correct the power factor of the supply side nearly to unity.
5. Conclusions
In this paper, a novel adaptive detection method for harmonic and reactive current is proposed. This method is analyzed systematically and verified by Matlab simulation. It is a continuously regulated closed-loop system, and the operating characteristics are nearly independent of the parameter variations of the elements, and bandwidth behaving as one of a second-order notch filter can be regulated easily by controlling the amplitude of the reference input and the gain of the integrator. Furthermore, this paper also introduces DC side voltage control method, which is simple and effective. Finally, simulation result is given to conform the feasibility of the design.
REFERENCES
- R. Bojoi, G. Griva, F. Profumo, M. Cesano, and L. Natale, “Shunt active filter implementation for induction heating applications,” Applied Power Electronics Conference and Exposion, Vol. 3, pp. 1674–1679, March 2005.
- D. Liu, B. D. Zhang, and X. L. Zhang, “Design of adaptive increment controlled hybrid-type active power filter,” Power and Energy Engineering Conference, Asia-Pacific, Vol. 27–31, No. 3, pp. 1–4. 2009.
- H. Akagi, E. H. Watanabe, and M. Aredes, “Instantaneous power theory and applications to power conditioning,” Wiley-Interscience a John Wiley & Sons, Inc., Publication, 2007.
- H. Akagi, “Generalized theory of instantaneous reactive power and its application,” Elec.Eng. in Japanese, April 1983.
- L. H. Tey and Y. C. Chu, “Improvement of power quality using adaptive shunt active filter,” IEEE Transactions on Power Delivery, Vol. 20, pp. 1558–1568, April 2005.
- B. Widrow and S. P. Sterns, “Adaptive signal processing,” Englewood Cliffs, Prentice-Hall, NJ, inc., 1985.
- J. H. Husy and M. S. E. Abadi, “Unified approach to adaptive filters and their performance,” IET Signal Process, Vol. 2, No. 2, pp. 97–109, 2008.
- A. Nakajima, “Development of active filter with series resonant circuit,” IEEE-PESC, Annual Meeting, pp. 1168–1173, 1988.
- Q. Wang, N. Wu, and Z. A. Wang, “A neuron adaptive detecting approach of harmonic current for apf and its realization of analog circuit,” IEEE Transactions on instrumentation and measurement,” Vol. 50, pp. 77–84, February 2001.
- H. P. To, F. Rahman, and C. Grantham, “An adaptive algorithm for controlling reactive power compensation in active power filters,” Industry Applications Conference, 39th IAS Annual Meeting, Vol. 1, pp. 3– 7, October 2004.
- L. P. Ling and A. Azli, “SVM based hysteresis current controller for a three phase active power filter,” Power and Energy Conference, pp. 132–136, November 2004.

