Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 2 (2012) , Article ID: 17620 , 9 pages DOI:10.4236/ijcns.2012.52016
MIMO Spectral Efficiency over Energy Consumption Requirements: Application to WSNs
1Departement Images et Signal (DIS), GIPSA-Lab, University of Grenoble, Grenoble, France
2Laboratory of Acoustics at University of Maine (LAUM), ENSIM, Le Mans, France
3TIC Departement, 6’COM, National Engineering School of Tunis (ENIT), Tunis, Tunisia
Email: maha.ben-zid@gipsa-lab.grenoble-inp.fr, kosai.raoof@univ-lemans.fr, ammar.bouallegue@enit.rnu.tn
Received November 11, 2011; revised January 9, 2012; accepted January 20, 2012
Keywords: MIMO Capacity; Energy Efficiency; Capacity to the Total Energy Consumption Ratio; Wireless Sensor Networks
ABSTRACT
This paper presents the evaluation of the “capacity to the total energy consumption per bit ratio” of multiple antennas systems with distributed fashion. We propose an adequate geometric channel modeling for the wireless communication system which operates in indoor propagation environment with scatterers. The channel model is derived in function of both the line of sight (LOS) and the non line of sight (NLOS) components. The aim of this paper is to study the limits in the gain concerning the capacity to the total energy consumption ratio when additional antennas are implemented in the communication system. To do so, we have evaluated by simulations both the capacity and the total energy consumption per bit. Then, we have determined the capacity to the total energy consumption ratio. Finally, the computational capacity to the total energy ratio is obtained for different system configurations. We have shown that the gain in capacity increases with the number of antennas but it stills be limited by the total energy consumption. The limits for increasing the number of transmit antennas are determined in function of the separation distances between the transmitter and the receiver sides of the communication system. Optimal power allocation strategy via water-filling algorithm has been carried out for evaluating the capacity to energy ratio. We find by simulation that optimal power allocation brings a gain in the addressed metric reaching a level of about 1.7 at transmit signal to noise ratio of 8 dB if comparing to the case when transmit energy is equally split among transmit antennas.
1. Introduction
Multiple Input Multiple Output (MIMO) technology refers to the use of multiple antennas at the transmitter and/ or multiple antennas at the receiver of the system communication. MIMO technology [1-4] has been shown to improve the communication system performance. It offers significant increases in spectral efficiency without additional bandwidth or transmit power. These features made MIMO technology attractive for several modern standards such as IEEE 802.11n, WiMax and 3GPP Long Term Evolution (LTE). We investigate the exploitation of MIMO systems in Wireless Sensor Networks (WSNs) where sensor nodes are miniature devices equipped with antennas. These nodes are randomly deployed in the sensing area and are assumed to operate until their batteries are exhausted. Therefore, energy management in such networks is a critical task. Throughout this paper, we show that even the use of multiple antennas system significantly improves the spectral efficiency of the communication system; it brings more requirements in terms of the total energy consumption per bit. The behavior of the cost in terms of the total energy consumption as a function of the maximum achieved system capacity is presented in this paper. This will contribute to optimal design for the low-power high-efficiency communication system which corresponds to the number of antennas for which we can get the lowest costs in energy consumption for a required level of system capacity.
The contribution of this paper falls into the category of distributed algorithms. As our work focuses on the distributed environment, it is worthwhile to address the information collection problem in the design process. In literature, many algorithms may be implemented for decision-making information collection. Among the existing algorithms for the decision-making algorithms, we perform the Code Division Multiple Access (CDMA) acquisition technique [5,6]. The best choice of decisionmaking strategy is such that signal synchronization can be achieved in the minimum time. However, it should be noticed that unlike the performed methodology works well, the performed algorithm presents a complexity during the synchronization process at the acquisition phase. In fact, the first step of processing at the receiver is to synchronize the generated pseudo-noise scrambling sequence to the tracking range of the received waveform. Nevertheless, the acquisition time is very long for longduration pseudo-noise sequences since its mean acquisition time is proportional to the pseudo noise sequence period as several correlations need to be employed.
2. Paper Organization
The remainder of this paper proceeds as follows. Section 3 gives an overview of the multiple antennas systems and introduces to the application of MIMO technology in wireless sensor networks. Section 4 presents the channel model according to an indoor propagation environment with rich scatterers. The analysis of the capacity to energy ratio is detailed in Section 5. Simulation results are presented and analyzed in Section 6. The improvement in the capacity to energy ratio via water-filling is evaluated in Section 7. Finally, concluding remarks are summarized in Section 8.
3. Multiple Antennas System: Application to WSN
3.1. Multiple Antennas System: An Overview
We introduce in this section the communication system model for multiple antennas system. We assume that  antennas are deployed at the transmitter and
antennas are deployed at the transmitter and  antennas are deployed at the receiver side as depicted in Figure 1. At the transmit side, each antenna
antennas are deployed at the receiver side as depicted in Figure 1. At the transmit side, each antenna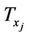 ;
;
 sends the signal
sends the signal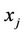 ;
;  to the receive antennas
to the receive antennas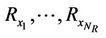 . Signals
. Signals ;
;

Figure 1. MIMO system model.
 pass through the radio propagation channel.
pass through the radio propagation channel.
The complex channel matrix  is given by:
is given by:

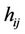 ,
,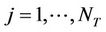 ;
;  denotes the complex channel gain which links the transmit antenna
denotes the complex channel gain which links the transmit antenna 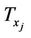 to the receive antenna
to the receive antenna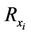 . At the receiver side, each receive antenna
. At the receiver side, each receive antenna 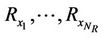 collects the incoming signals from the
collects the incoming signals from the 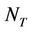 transmit antennas which add up coherently. The received signals at antennas
transmit antennas which add up coherently. The received signals at antennas 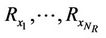 are respectively denoted in Figure 1 by
are respectively denoted in Figure 1 by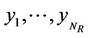 . The received signal at antenna
. The received signal at antenna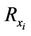 ;
; 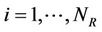 with additive noise signal
with additive noise signal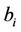 ;
;  is given by:
is given by:
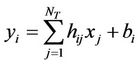 ;
;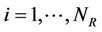 (1)
(1)
From matrix notations where:
· 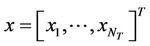 is the
is the  complex vector for the transmitted signal.
complex vector for the transmitted signal.
·  is the
is the 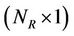 complex vector for the received signal.
complex vector for the received signal.
· 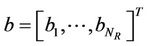 is the
is the 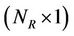 complex vector for the additive noise signal.
complex vector for the additive noise signal.
The multiple antennas system model is described by the input output relationship as:
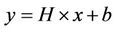 (2)
(2)
3.2. MIMO Approach for WSNs
The work addressed in this paper is not limited to the MIMO systems. The structure of MIMO system is assumed to be performed by Wireless Sensor Networks (WSNs). The approach of MIMO systems is summarized in Figure 2 where  sensor nodes
sensor nodes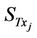 ; j = 1,
; j = 1, NTare available at the transmit side and
NTare available at the transmit side and  sensor nodes
sensor nodes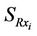 ;
; 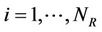 are considered at the receive side. Each sensor node
are considered at the receive side. Each sensor node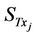 ;
; 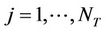 transmits its information
transmits its information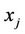 ;
; 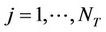 to all the other sensor nodes at the receiver side following the model described by Equation (2).
to all the other sensor nodes at the receiver side following the model described by Equation (2).
4. Channel Modeling
The Rician fading channel modeling is performed in this work. We assume that the channel coefficients vary in function of the square value of the separation distance between the transmitter and the receiver. The channel matrix coefficients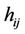 ;
; ;
;  are given by:
are given by:
 (3)
(3)
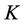 is the Rician coefficient.
is the Rician coefficient.
The performed communication scenario assumes a rich scattering propagation environment with 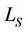 scatterers as depicted in Figure 3.
scatterers as depicted in Figure 3.
The NLOS components are expressed as:
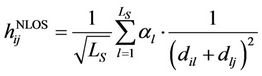 (4)
(4)
· 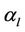 is a random scattering coefficient from the
is a random scattering coefficient from the 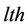 scatterer,
scatterer, .
.
·  is the distance between the
is the distance between the 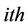 receive antenna and the
receive antenna and the 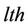 scatterer,
scatterer, ;
; .
.
·  is the distance between the
is the distance between the  scatterer and the
scatterer and the 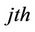 transmit antenna,
transmit antenna, ;
; 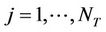
The LOS components are given by:
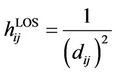 (5)
(5)
· 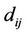 is the distance between the
is the distance between the  receive antenna
receive antenna

Figure 2. MIMO approach for WSNs.

Figure 3. Propagation environment with scatterers.
and the 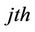 transmit antenna,
transmit antenna,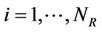 ; j = 1,
; j = 1, , NT.
, NT.
5. Capacity to Energy Ratio Analysis
The metric 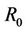 [7] given by Equation (6) measures the capacity to the total energy consumption per bit ratio.
[7] given by Equation (6) measures the capacity to the total energy consumption per bit ratio.
 (6)
(6)
· 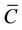 is the ergodic system capacity (in bits/s/Hz) given as the expectation value of the instantaneous channel capacity over channel matrices realizations.
is the ergodic system capacity (in bits/s/Hz) given as the expectation value of the instantaneous channel capacity over channel matrices realizations.
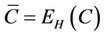 (7)
(7)
· 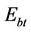 is the total energy consumption per bit (in J).
is the total energy consumption per bit (in J).
The computation of both the system capacity and the total energy consumption are detailed in the following sections.
5.1. Channel Capacity Evaluation
When no channel state information (CSI) is available at the transmitter, the transmit energy is equally split between the  antennas. As such, the instantaneous channel capacity [1] associated to the multiple antennas communication system model is given by:
antennas. As such, the instantaneous channel capacity [1] associated to the multiple antennas communication system model is given by:
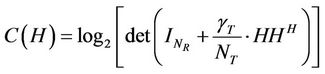 bits/s/Hz (8)
bits/s/Hz (8)
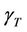 denotes the transmit signal to noise ratio.
denotes the transmit signal to noise ratio.
Case of available channel state information at both the transmitter and the receiver, the channel capacity may be computed in more optimal way by performing the waterfilling algorithm [8]. The instantaneous channel capacity with water-filling is then:
 bits/s/Hz (9)
bits/s/Hz (9)
· 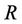 is the rank of the channel matrix H.
is the rank of the channel matrix H.
·  is the noise signal power.
is the noise signal power.
·  .
.
· 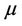 is a constant scalar that satisfies the total power constraint.
is a constant scalar that satisfies the total power constraint.
· 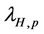 is the
is the  singular value of the channel matrix H.
singular value of the channel matrix H.
In the following, we consider normalization for the channel matrix 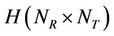 so that the power channel
so that the power channel  satisfies:
satisfies:
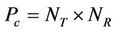
Where:
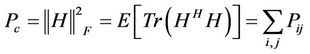 ;
; 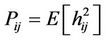 (10)
(10)
· 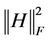 is the Frobenius norm.
is the Frobenius norm.
· 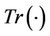 is the trace operator.
is the trace operator.
Based on the channel modeling that we have presented previously, we consider a MIMO system of dimensions 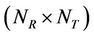 where the number of transmit antennas is variable and the number of receive antennas is fixed to 4. The simulation of system capacity is presented for different transmit signal to noise ratios
where the number of transmit antennas is variable and the number of receive antennas is fixed to 4. The simulation of system capacity is presented for different transmit signal to noise ratios 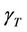 of 2 dB, 4 dB and 8 dB. The separation distance between the transmitter and the receiver, d equals 20 meters. The variation of the system capacity as a function of the number of transmit antennas when performing water-filling is presented in Figure 4. The simulated ergodic capacity via waterfilling algorithm is shown to be improved as well as more antennas are deployed at the transmitter and more energy is allocated.
of 2 dB, 4 dB and 8 dB. The separation distance between the transmitter and the receiver, d equals 20 meters. The variation of the system capacity as a function of the number of transmit antennas when performing water-filling is presented in Figure 4. The simulated ergodic capacity via waterfilling algorithm is shown to be improved as well as more antennas are deployed at the transmitter and more energy is allocated.
5.2. Total Energy Consumption per Bit Evaluation
We evaluate the power consumption for each antenna at both the transmit and receive sides. For a given bit rate level, the energy consumption could be then deduced. Our analysis is based on the model of the transmitter block with complex modulator and the model of the receiver block as shown in Figures 5 and 6. These models are respectively performed by each transmit and receive antenna. The total power consumption [9,10] is evaluated in function of:
1) The power consumption of the amplifiers, .
.
2) The power consumption of the circuit blocks,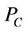 .
.
The power consumption of the amplifiers is expressed as:
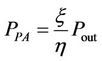 (11)
(11)
·  is the peak to average ratio which is expressed as a
is the peak to average ratio which is expressed as a
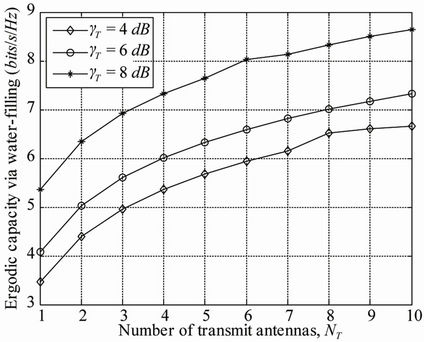
Figure 4. Multiple antennas system capacity with waterfilling, d = 20 m.
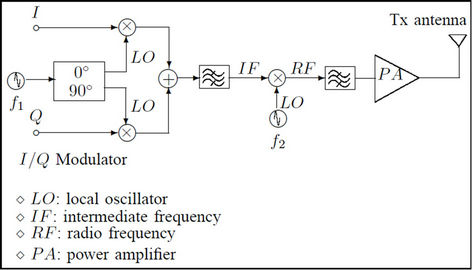
Figure 5. Transmit block diagram.
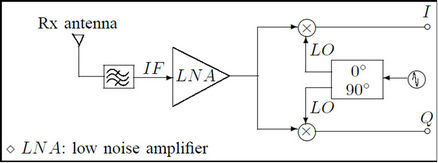
Figure 6. Receiver block diagram.
function of the modulation constellation size M by:
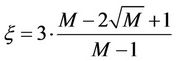 (12)
(12)
·  is the drain efficiency.
is the drain efficiency.
The output power for a separation distance between the transmitter and the receiver d is expressed as:
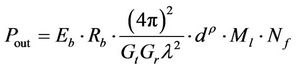 (13)
(13)
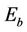 is the transmission energy per bit. For a required bit error rate, denoting the receive signal to noise ratio at each receive antenna by
is the transmission energy per bit. For a required bit error rate, denoting the receive signal to noise ratio at each receive antenna by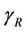 , when the transmit power is equally allocated to the
, when the transmit power is equally allocated to the 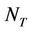 transmit antennas, the average error probability is:
transmit antennas, the average error probability is:
 (14)
(14)
· 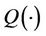 denotes the Marcum function.
denotes the Marcum function.
An upper bound for the required energy per bit satisfies [9]:
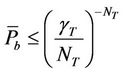 (15)
(15)
·  is the bit rate.
is the bit rate.
· 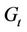 is the transmit antenna gain.
is the transmit antenna gain.
· 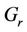 is the receive antenna gain.
is the receive antenna gain.
· 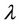 is the wavelength.
is the wavelength.
· 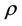 is the path loss exponent. The path loss exponent is assumed to be the same for all the propagation links. For indoor propagation environment, the path loss exponent at a carrier frequency of 2.4 GHz equals 3.3 [11].
is the path loss exponent. The path loss exponent is assumed to be the same for all the propagation links. For indoor propagation environment, the path loss exponent at a carrier frequency of 2.4 GHz equals 3.3 [11].
· 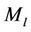 is the link margin.
is the link margin.
· 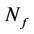 is the receiver noise figure.
is the receiver noise figure.
The total power consumption is evaluated by computing the power consumption of both the transmitter circuit blocks and the receiver circuit blocks of multiple antennas systems with  transmit antennas and
transmit antennas and  receive antennas as:
receive antennas as:
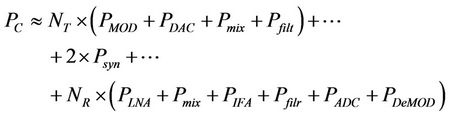 (16)
(16)
· 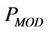 : power consumption of the modulator.
: power consumption of the modulator.
·  : power consumption of the digital-to-analog converter.
: power consumption of the digital-to-analog converter.
· 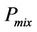 : power consumption of the mixer.
: power consumption of the mixer.
· 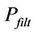 : power consumption of the active filter at the transmitter.
: power consumption of the active filter at the transmitter.
· 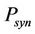 : power consumption of the frequency synthesizer.
: power consumption of the frequency synthesizer.
·  : power consumption of the low-noise amplifier.
: power consumption of the low-noise amplifier.
· 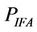 : power consumption of the intermediate frequency amplifier.
: power consumption of the intermediate frequency amplifier.
· 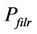 : power consumption of the active filter at the receiver.
: power consumption of the active filter at the receiver.
· 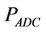 : power consumption of the analog-to-digital converter.
: power consumption of the analog-to-digital converter.
·  : power consumption of the demodulator.
: power consumption of the demodulator.
Finally, we express the total energy consumption per bit as:
 (17)
(17)
6. Simulation Results and Observations
In order to evaluate the metric “capacity to energy ratio”, we have carried out a computer based Monte-Carlo simulation for both the distributed MIMO system capacity and the total energy consumption per bit following the communication system model as introduced in Section 3.1. Table 1 summarizes the system setting. The number of receiver antennas  is set to 4. The metric “capacity to energy ratio” is evaluated for different transmitter configurations with variable number of transmit antennas
is set to 4. The metric “capacity to energy ratio” is evaluated for different transmitter configurations with variable number of transmit antennas .
.
6.1. Energy Simulation
We investigate the analysis of the effect of separation distance between the transmitter and the receiver on the “capacity to energy ratio” for each transmitter antennas configuration. The total energy consumption per bit is simulated for separation distances between the transmitter and the receiver in the range from 1 m to 20 m.
Figure 7 shows the plotted curves of the total energy consumption as a function of the number of transmit antennas for different separation distances between the transmitter and the receiver. The total energy consumption per bit is shown to increase as well as more antennas are deployed at the transmitter. We report in Table 2, the growth in energy consumption when comparing to the total energy consumption of MMO (4 × 1). The transmit signal to noise ratio is  = 8 dB and the separation distance between the transmitter and the receiver is set to
= 8 dB and the separation distance between the transmitter and the receiver is set to
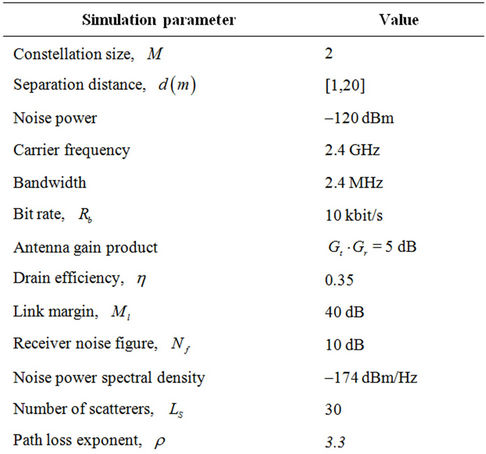

Table 1. Simulation parameters.

Table 2. Growth in the total energy consumption per bit with various number of antennas.
d = 10 m. The impact of the separation distance on energy consumption is evaluated in Table 3. Here, we are evaluating the growth in energy consumption when comparing the separation distance between the transmitter and the receiver of 10 m and 20 m.
In the following, we propose to examine the behavior of the total energy consumption per bit for different contellation sizes at fixed transmit signal to noise ratio of 8 dB and number of transmit antennas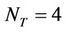 . The total energy consumption per bit is presented in Figure 8 as a function of the separation distance between the transmitter and the receiver d for various modulation constella-
. The total energy consumption per bit is presented in Figure 8 as a function of the separation distance between the transmitter and the receiver d for various modulation constella-
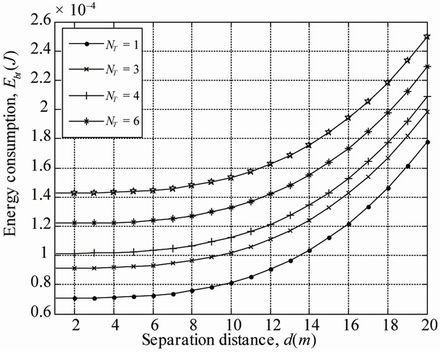
Figure 7. Total energy consumption per bit over separation distance and variable number of transmit antennas.

Table 3. Growth in the total energy consumption per bit with various separation distances.
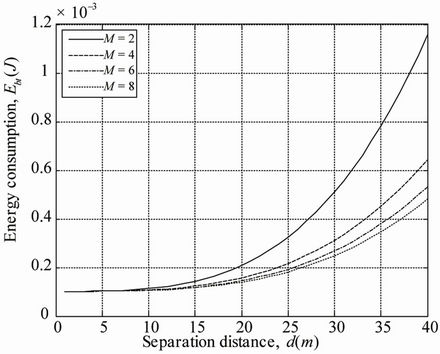
Figure 8. Energy consumption for various constellation sizes, M.
tion sizes M = 2, M = 4, M = 6 and M = 8. The presented results show that higher modulation constellation size permits saves in the total energy consumption. The gain in the total energy consumption is more important for higher separation distances between the transmitter and the receiver.
Table 4 evaluates the saving in the total energy consumption in function of the constellation size expressed as:
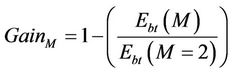 (18)
(18)
As we have shown by simulation in Section 5.1 that the use of multiple antennas considerably improves the communication system capacity as well as how the use of multiple antennas could be costly in the total energy consumption per bit in Section 6.1, we propose in the following to evaluate the limits in the use of additional antennas that stills improve the capacity to energy ratio, .
.
6.2. Capacity to Energy Ratio Simulation
The metric “capacity to energy ratio” represents the amount of energy required for a given system capacity. The simulation of the metric  is targeted to examine how much the use of additional antennas could improve the metric “capacity to energy ratio”. The simulation results of the metric
is targeted to examine how much the use of additional antennas could improve the metric “capacity to energy ratio”. The simulation results of the metric  are sketched in Figure 9. We assume that the transmit energy is equally split between the
are sketched in Figure 9. We assume that the transmit energy is equally split between the 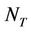 antennas. Figure 10 shows that the metric
antennas. Figure 10 shows that the metric 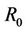 decreases in function of the separation distance between the transmitter and the receiver.
decreases in function of the separation distance between the transmitter and the receiver.
The behavior of the capacity to energy ratio over distance 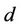 is expected since the capacity decreases in function of the separation distance and the total energy consumption per bit is increased. We also find by simulation that
is expected since the capacity decreases in function of the separation distance and the total energy consumption per bit is increased. We also find by simulation that  decreases in function of the number of antennas
decreases in function of the number of antennas  as sketched in Figure 11.
as sketched in Figure 11.
6.3. Capacity to Energy Ratio: Water-Filling
We investigate in this section, the use of water-filling algorithm on the simulation of the capacity to energy ratio,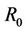 . Figure 12 shows the variation of the capacity to energy ratio for different separation distances. We
. Figure 12 shows the variation of the capacity to energy ratio for different separation distances. We

Table 4. Impact of the constellation size on the total energy consumption per bit.
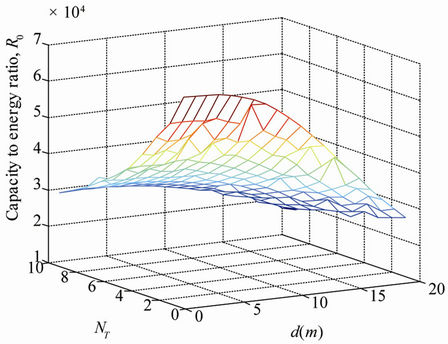
Figure 9. Capacity to energy ratio over the number of transmit antennas and separation distances, M = 2.
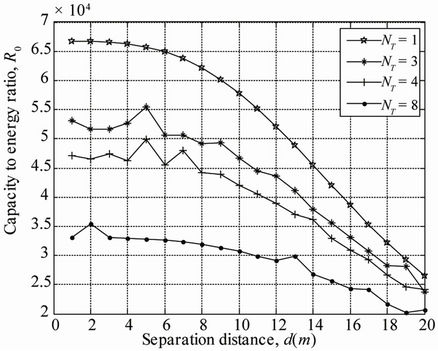
Figure 10. Capacity to energy ratio for various separation distances.

Figure 11. Capacity to energy ratio for various number of transmit antennas.
keep our comments as previously concerning the behavior of R0 which decreases in function of the separation distance between the transmitter and the receiver, d. The variation of  in function of the antenna number is sketched in Figure 13 (
in function of the antenna number is sketched in Figure 13 ( = 8 dB) and Figure 14 (
= 8 dB) and Figure 14 (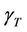 = 3 dB).
= 3 dB).
The capacity to energy ratio grows with the number of transmit antennas but it is shown to be limited by the number of receive antennas . All possible variations of the capacity to energy ratio at
. All possible variations of the capacity to energy ratio at  = 3 dB are reported in Figure 15.
= 3 dB are reported in Figure 15.
7. Improvement in the Capacity to Energy Ratio via Water-Filling
We evaluate in this section, via a comparative analysis the ratio between the metric obtained via water-filling and that one when no water-filling is performed. 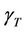 is set to 8 dB and M equals 2. Figure 16 depicts the gain in the metric
is set to 8 dB and M equals 2. Figure 16 depicts the gain in the metric  when power is optimally allocated among the transmit antennas. The improvement in the capacity to energy ratio
when power is optimally allocated among the transmit antennas. The improvement in the capacity to energy ratio  is presented for different separation
is presented for different separation
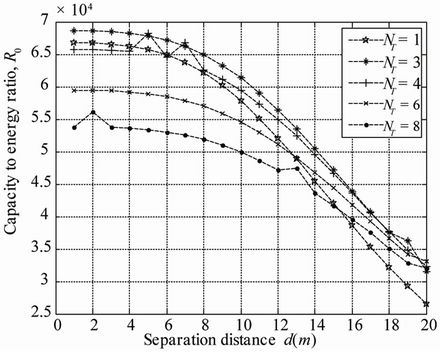
Figure 12. Capacity to energy ratio over separation distance (water-filling).

Figure 13. Capacity to energy ratio over the number of transmit antennas (water-filling), γT = 8 dB.
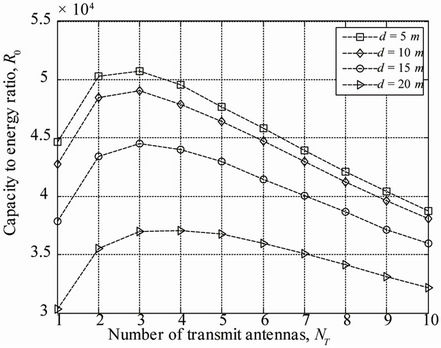
Figure 14. Capacity to energy ratio over the number of transmit antennas (water-filling), γT = 3 dB.

Figure 15. Simulated capacity to energy ratio via waterfilling, γT = 3 dB.

Figure 16. Improvement in the capacity to energy ratio via water-filling.
distances between the transmitter and the receiver but seems to be insensible to the separation distance between the transmitter and the receiver. The improvement in the
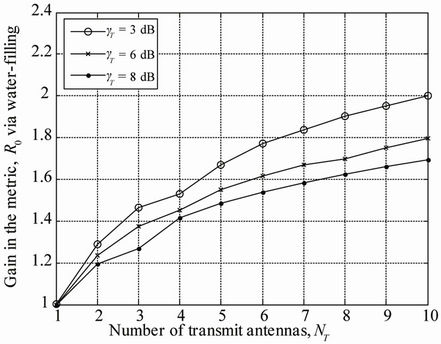
Figure 17. Improvement in the capacity to energy ratio via water-filling for different SNRs, γT.
capacity to the total energy ratio is presented at separation distance of 10 m in Figure 17 when different levels of the transmit signal to noise ratio,  are considered. As depicted in Figure 17, the gain in the metric
are considered. As depicted in Figure 17, the gain in the metric 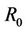 is more important for the lowest transmit signal to noise ratio
is more important for the lowest transmit signal to noise ratio .
.
8. Conclusion
Throughout this paper, we have made the analysis of the capacity to the total energy consumption per bit for multiple antennas systems with fixed number of receive antennas and various number of transmit antennas. To do so, the metric 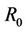 has been introduced in order to evaluate the cost in energy consumption for a given amount of the communication system capacity. Our analysis has been carried out over the Rician channel model with scatterers. Simulation of the capacity to energy ratio has been presented for variable number of transmit antennas and different ranges of the separation distances between the transmitter and the receiver. We have presented our results when optimal transmit power allocation is exploited and we have shown that even the use of multiple antennas improves the system capacity, it stills be limited by the total energy consumption. The IEEE 802.15.4 standard and ZigBee wireless technology could be considered for the evaluation of the presented communication model and could be then tested easily via a simple method of data routing.
has been introduced in order to evaluate the cost in energy consumption for a given amount of the communication system capacity. Our analysis has been carried out over the Rician channel model with scatterers. Simulation of the capacity to energy ratio has been presented for variable number of transmit antennas and different ranges of the separation distances between the transmitter and the receiver. We have presented our results when optimal transmit power allocation is exploited and we have shown that even the use of multiple antennas improves the system capacity, it stills be limited by the total energy consumption. The IEEE 802.15.4 standard and ZigBee wireless technology could be considered for the evaluation of the presented communication model and could be then tested easily via a simple method of data routing.
REFERENCES
- K. Raoof, M. Ben Zid, N. Prayongpun and A. Bouallègue, “Advanced MIMO Techniques: Polarization Diversity and Antenna Selection,” 2011. http://www.intechopen.com
- K. Raoof and H. Zhou, “Advanced MIMO Systems,” Scientific Research Publishing, USA, 2009.
- M. Ben Zid, K. Raoof and A. Bouallègue, “MIMO Systems and Cooperative Networks Performances,” In: K. Raoof, et al., Eds., Cognitive Radio, Scientific Research Publishing, USA, 2011, pp. 113-140.
- E. Biglieri, R. Calderbank, A. Constantinides, A. Goldsmith and A. Paulraj, “MIMO Wireless Communications,” Cambridge University Press, Cambridge, 2007.
- B. Lang, T. Han and X. Gu, “A Robust Non-Coherent Sequential Code Acquisition Scheme for DS/SS Communications,” Proceedings of the 9th International Conference on Signal Processing (ICSP’08), Beijing, 26-29 October 2008, pp. 1939-1942.
- G. S. Hosangadi and C. W. Baum, “Hybrid Sequential Acquisition Schemes for Noncoherent Chip-Asynchronous DS/SS Systems,” Proceedings of the IEEE International Conference on Communications (ICC’98), Atlanta, 7-11 June 1998, pp. 1242-1247.
- M. Ben Zid, K. Raoof and A. Bouallègue, “A Novel Metric for Measuring Multiple Antennas System Capacity over Energy Consumption Requirements,” Proceedings of the 7th International Conference Wireless Communications, Networking and Mobile Computing (WiCOM), Wuhan, 23-25 September 2011, pp. 1-4.
- M. A. Khalighi, J.-M.Brossier, G. V. Jourdain and K. Raoof, “Waterfilling Capacity of Rayleigh MIMO Channels,” Proceedings of the 12th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, San Diego, 30 September-3 October 2001, pp. 155-158.
- S. Cui, A. J. Goldsmith and A. Bahai, “Energy-Efficiency of MIMO and Cooperative MIMO Techniques in Sensor Networks,” IEEE Journal on Selected Areas in Communications, Vol. 22, No. 6, 2004, pp. 1089-1098. doi:10.1109/JSAC.2004.830916.
- S. Cui, A. J. Goldsmith and A. Bahai, “Energy-Constrained Modulation Optimization,” IEEE Transactions on Communications, Vol. 4, No. 5, 2005, pp. 2349-2360.
- K. Kaemarungsi and P. Krishnamurthy, “Modeling of Indoor Positioning Systems Based on Location Fingerprinting,” Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies, Hong Kong, March 2004, pp. 1012-1022.

