Int'l J. of Communications, Network and System Sciences
Vol.3 No.1(2010), Article ID:1174,5 pages DOI:10.4236/ijcns.2010.31007
A User Selection Method in Advertising System
Pattern Recognition & Intelligent System Lab,Beijing University of Posts and Telecommunications, Beijing, China
E-mail: xiongshiyi@gmail.com, {linzq, xiaobo}@bupt.edu.cn
Received October 27, 2009; revised November 28, 2009; accepted December 30, 2009
Keywords: User Selection, Maximum Frequent Itemsets, Bayesian Network
Abstract
It’s important for mobile operators to recommend new services. Traditional method is sending advertising messages to all mobile users. But most of users who are not interested in these services treat the messages as Spam. This paper presents a method to find potential customers who are likely to accept the services. This method searchs the maximum frequent itemsets which indicate potential customers’ features from a large data set of users’ information, then find potential customers from those maximum frequent itemsets by using a bayesian network classifier. Experimental results demonstrate this method can select users with higher accuracy.
1. Introduction
Recent years, as the increasing number of mobile operators and new services, the competition between operators becomes more and more furious. The key of the competition is to win more customers. How to introduce new services to proper customers becomes one of the major problems.
Now, advertising system mostly uses these technologies: collaborative filtering technology [1] , content based recommendation, knowledge based recommendation, efficiency based recommendation, association rules based recommendation [2] , etc. These methods are usually used to select and recommend products to specified users. They analyse the user’s historical data and predict what products the user mostly need. For example, an online movie system uses one of above technologies to serve its user whose name is Mike. The system will analyse Mike’s history and recommend him some movies in which he may be interested. So we can say these methods solve the problem to select products for users.
The proplem we desire to solve in this paper is a little different. Here we have only one product, namely the new mobile service, and we want to know which users want to buy this service. Those users are potential customers, and we need to pick out them from a large number of users. The problem is to select users for one product. As a result, those traditional methods will not work well on this problem.
This paper presents a new method to select users. This method searchs the maximum frequent itemsets from a large data set, then find potential customers from those maximum frequent itemsets by using a bayesian network classifier.
2. Analysis of Customer Features
Usually, mobile operators keep a large database of consumption data. This data includes the items that represent customers’ features, such as the telephone fees of every month, function fees and information fees, etc. This data also shows whether a customer accepts the new service, those customers who accept new service can be seen as positive samples, and others can be seen as negative samples. As a result, the problem to select positive samples can be treated as a two-category classification problem.
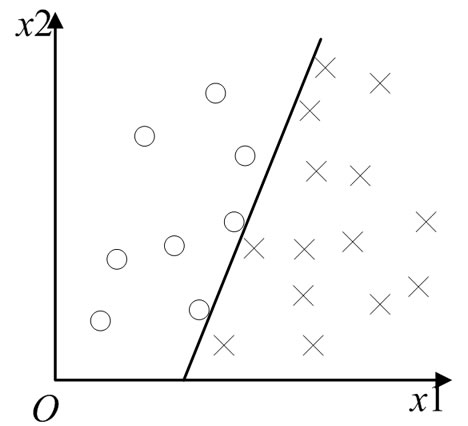
Usually, two-category classification problem should have data with features shown in Figure 1 (a). However, the mobile users’ data are quite different (shown in Figure 1 (b). For example, some users who have the same features may belong to different categories. What’s more, number of negative samples is much larger than the number of positive sample. Because of this, routine classification methods such as naive bayesian classifier is hard to classfy such data.
3. Frequently Itemsets
3.1. Fomal Model of Frequently Itemsets
Let sample has
has dimensions(Attributes) and the value may be continuous. Divide the value into several seg-
dimensions(Attributes) and the value may be continuous. Divide the value into several seg-
 (a)
(a)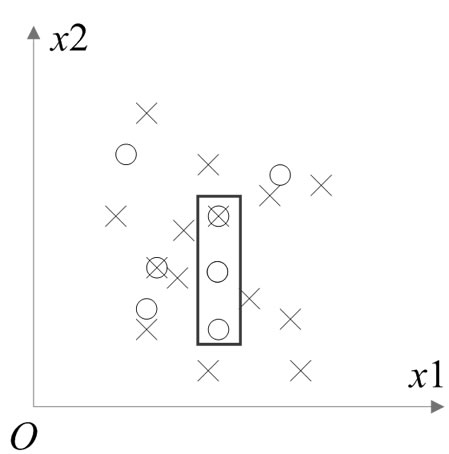 (b)
(b)
Figure 1. Feature distribution map. (a) Two-category classification; (b) Mobile users’ data.
ments and give each segment a unique serial code. Because each sample belongs to an segment, we can use the corresponding segment code to replace this sample. In this way, original samples are mapped to the segment codes
are mapped to the segment codes :
: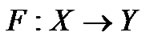 .
.
Divide the original samples uses the following guidelines:
1) The number of positive samples in each segment is uniformly distributed.
2) Each Attributes should have the same number of segments.
Make each Attribute divided into k segments so that the segments code should not bigger than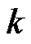 . If the value of a Attrubutes is a 0-1 type value, the number of segments code should be
. If the value of a Attrubutes is a 0-1 type value, the number of segments code should be , not
, not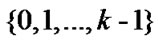 .
.
The Attribute segment 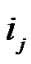 is called item. The Attribute segment combination of
is called item. The Attribute segment combination of 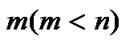 attributes
attributes  is called itemsets.
is called itemsets.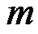 is length of the itemsets
is length of the itemsets . If a sample’s attribute segments in
. If a sample’s attribute segments in 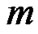 dimensions are
dimensions are , we call this sample satisfied the itemsets
, we call this sample satisfied the itemsets .
.
If an itemsets has positive sample number  while has negative sample number
while has negative sample number ,
,  is the success rate of itemsets
is the success rate of itemsets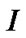 . Given a minimum support threshold
. Given a minimum support threshold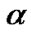 . If
. If 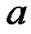 >
>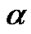 , we call
, we call 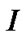 frequent itemsets.
frequent itemsets.
3.2. Frequent Close Itemset
Given 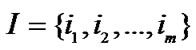 be an itemsets with length m, add an item of attribute
be an itemsets with length m, add an item of attribute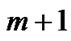 into
into , so
, so  has the length
has the length . If
. If and
and have the same number of positive samples, then
have the same number of positive samples, then . This can be proofed as below:
. This can be proofed as below:
Suppose both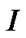 and
and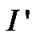 have
have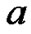 positive samples.
positive samples.  has
has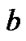 negative samples, while
negative samples, while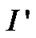 has
has . Since
. Since has one more item
has one more item ,we can get
,we can get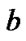 ≥
≥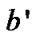 . Thus
. Thus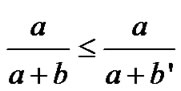 , that is
, that is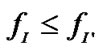 , and
, and has a higher success ratio.
has a higher success ratio.
In case of , ignore the itemsets
, ignore the itemsets , and keep
, and keep . When
. When ,
,  is called frequent close itemsets(ab. FCI). There are some typical algorithm to mine frequent close itemsets such as Apriori [3] and FP2Tree [4] .
is called frequent close itemsets(ab. FCI). There are some typical algorithm to mine frequent close itemsets such as Apriori [3] and FP2Tree [4] .
As a part of the user selection method, samples in the FCI should be predicted using Bayesian network classifier. Given the number of attributes  and the number of segments
and the number of segments , then the number of itemsets is:
, then the number of itemsets is:

The number has an exponential growth, so it’s impossible to construct a Bayesian network classifier for all itemsets. A compromised way is colleting all of the samples to be one data set and construct a Bayesian network classifier based on this data set.
4. Bayesian Network Model for User Selection
4.1. Bayesian Network Basics
A Bayesian network is a graphical model that encodes relationships among variables of interest. A Bayesian network consists of a set of nodes and a set of directed edges between nodes [5] , which shown in Figure 2 . In general, a Bayesian network is expressed as sign , which consists of the following two parts [6] .
, which consists of the following two parts [6] .
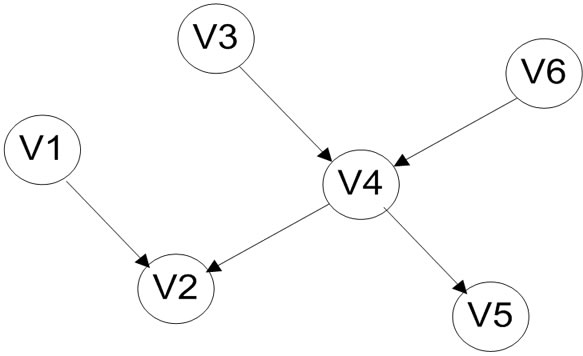
Figure 2. Typical graphic model of Bayesian networks.
1) A directed acyclic graph with
with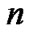 nodes. The nodes of the graph represent random variables or events. The directed edges between nodes in the graph represent the causal relationships of the nodes. The important concept in Bayesian networks is the conditional independence between variables. For any variable
nodes. The nodes of the graph represent random variables or events. The directed edges between nodes in the graph represent the causal relationships of the nodes. The important concept in Bayesian networks is the conditional independence between variables. For any variable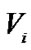 , the parent variables of
, the parent variables of  is
is , the
, the 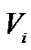 is independent of the variables set
is independent of the variables set , which is the set of the variables that are not child variables of
, which is the set of the variables that are not child variables of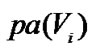 , so the probability of
, so the probability of  is calculated as:
is calculated as:

2) A conditional probabilities table (ab. CPT) associated with each node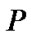 . The CPT is expressed as
. The CPT is expressed as  which pictures the mutual relationship of each node and its parent nodes. Nodes with no parent have a very simple probability table, giving the prior probability distribution of the node. Nodes with parents are much more complicated. These nodes have conditional probability tables, which give a probability distribution for every combination of states of the variable’s parents.
which pictures the mutual relationship of each node and its parent nodes. Nodes with no parent have a very simple probability table, giving the prior probability distribution of the node. Nodes with parents are much more complicated. These nodes have conditional probability tables, which give a probability distribution for every combination of states of the variable’s parents.
The Bayesian network can represent all of the nodes’ joint probability due to the node relationship and the conditional probability table. Applying the conditional independence into the chain rule, we get the following expression:
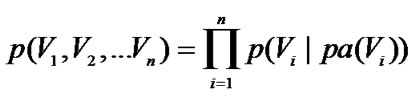
4.2. Bayesian Network Structure Learning
Consider a finite set  of discrete random variables where each variable
of discrete random variables where each variable 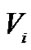 may take on values from a finite set, denoted by
may take on values from a finite set, denoted by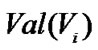 . Formally, a Bayesian network for
. Formally, a Bayesian network for  is a pair
is a pair , and defines a unique joint probability distribution over
, and defines a unique joint probability distribution over . The problem of learning a Bayesian network can be informally stated as: Given a training set
. The problem of learning a Bayesian network can be informally stated as: Given a training set
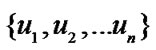 of instances of U, find a network
of instances of U, find a network  that best matches D. The common approach to this problem is to introduce a scoring function that evaluates each network with respect to the training data, and then to search for the best network according to this function. The two main scoring functions commonly used to learn Bayesian networks are the Bayesian scoring function [8] , and the function based on the principle of minimal description length (ab. MDL) [7] . We only introduce MDL scoring function. The MDL scoring function of a network
that best matches D. The common approach to this problem is to introduce a scoring function that evaluates each network with respect to the training data, and then to search for the best network according to this function. The two main scoring functions commonly used to learn Bayesian networks are the Bayesian scoring function [8] , and the function based on the principle of minimal description length (ab. MDL) [7] . We only introduce MDL scoring function. The MDL scoring function of a network  given a training data set
given a training data set , written
, written , is given by following expresion:
, is given by following expresion:

where 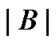 is the number of parameters in the network. The second term is the negation of the log likelihood of
is the number of parameters in the network. The second term is the negation of the log likelihood of 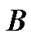 given
given :
:

Bayesian network structure learning is NP problem, now typical method has K2 [8] developed by Cooper and Hers2kovits.
5. Model of Selection Method
The method searchs the maximum frequent itemsets from a large data set, then find potential customers from those maximum frequent itemsets by using a bayesian network classifier. In detail, we can get result by taking following steps:
1) All users share the same attributes. For each attribute, users have different values from each other. We get all sample’s values of each attribute from the data set, and divide these values into k segments using the method presented in Subsection 2.2.1.
2) Based on the data processing in step 1, set a minimum support number and mine all of the FCI.
3) Every FCI contain a certain number of samples, collect these samples and make them to be a new data set .
.
4) Learn bayesian network from data set which is formed in step 3, using K2 algorithm.
which is formed in step 3, using K2 algorithm.
5) For samples without knowing is positive or is negative, calculate its positive probability by bayesian network constructed in 4. Once we get the probability, we can get result by comparing it with given threshold.
If a user is predicted to be positive, then the recommendation system will send the advertisement message to this user. On the other hand, user who are predicted to be negative will not receive advertisement messages.
6. Experiment
In experiments we try the new method as well as method based on naive bayesian claasifier so that we can compare the results between both methods.
6.1. Classify Using Naive Bayesian Classifier
1) Discretize the values and train naive bayesian classifier.
2) Give a decision threshold and classify the test data set using the trained naive bayesian classifer. Results are shown in Table 1 .

Figure 3. Success rate for different segments number.

Figure 4. Success rate for different Minimum support number.
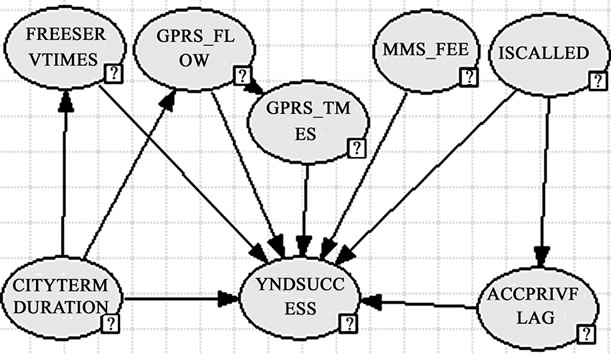
Figure 5. Bayesian network learned by GENIE.
6.2. Steps of New Method
1) We divide the values of each attribute into k segments. While k is 10, 20, 30 respectivly, the results are shown in Figure 3 . It shows that the best result occurs while k is 10.
2) Given a minimum support number  and search FCI, then compare the experimental results when
and search FCI, then compare the experimental results when  is 10, 20, 30, 40, 50 respectivly. The results are shown in Figure 4 . It shows that we get the highest success rate while
is 10, 20, 30, 40, 50 respectivly. The results are shown in Figure 4 . It shows that we get the highest success rate while  is 50. We don’t consider a minimum support number larger than 50 because the coverage of potential customer will decrease too much, see the data in Table 2 .
is 50. We don’t consider a minimum support number larger than 50 because the coverage of potential customer will decrease too much, see the data in Table 2 .
3) Learn bayesian network from D using a open source bayesian tool called GENIE (http://genie.sis.pitt.edu), which uses K2 algorithm to learn Bayesian network structure. We get a Bayesian network shown in Figure 5 , where GPRS_ FLOW, MMS_FEE, etc are names of attributes. YNDSUCCESS is the target attribute to be predicted.
4) Last step is predicting by Bayesian network classifier. Since the number of negative samples is much more large than number of positive samples, we set the threshold to be 0.1. That means if a sample has a probability to be positive sample larger than 0.1, then it is determined to be positive.
6.3. Experimental Results
In this experiment, we use a data set from a mobile service provider. We divide the users into two parts. One part with the user number of 12264 is training data set. The other part with 12263 users including 577 positive users is test data set.
For traditional method which sends advertising message to all users. It sends 12264 advertisements and gets 577 customers, the success rate is 4.7%. It sends advertisement to 100% of the users, and gets 100% of the potential customers.
For method based on naïve Bayesian classifier whose results shown in Table 1 , the results are almost the same as the results of traditional method. Obviously, naïve Bayesian classifier does not work well with mobile user’s data set.
For new method, the results are shown in Table 2 . Take mininum support number 50 for example, it sends 1621 advertisements and gets 303 customers, the success rate is 18.69%. It sends advertisement to 13.22% of all users, and gets 49.78% of the potential customers.
The results show that this user selection method increases success rate efficiently. Even the lowest success

Table 1. Results of naïve Bayesian classifier.
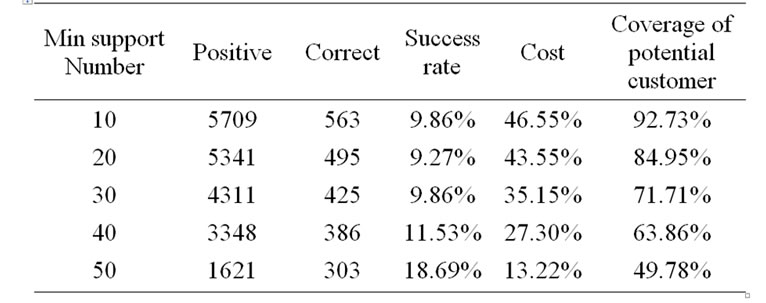
Table 2 Experiment result.
rate 9.85%, is dramatically higher than the success rate of traditional method and of naïve Bayesian classifier. It also saves advertising cost and cuts down Spam remarkably.
7. Conclusions
Recomendation system becomes more and more important to service providers now. User selection is one of the difficulty problems. This paper presents a method to select users, the method searchs the maximum frequent itemsets from a large data set, then find potential customers from those maximum frequent itemsets by using a bayesian network classifier. The success rate is improved dramatically after using the method. This method also cuts down advertisement cost for mobile operators and avoids making large number of Spam messages.
There are a lot of data sets which have similar features with mobile user’s data set, so this method can be used in many similar advertising recommendation systems. It has a good universality.
8. Acknowledgement
This work was supported by the national High-tech Research and Development Plan of China under grant No.2007AA01Z417 and the 111 Project of China under grant No. B08004.
9. References
[1] E. Rich, “User modeling via stereotypes [D],” Cognitive Science, Vol. 3, No. 4, pp. 329–354, 1979.
[2] U. M. Fayyad, G. Piatecsky-Shapiro, and P. Smyth, “Advances in knowledge discovery and data mining [M],” California, AAAI/MIT Press, 1996.
[3] R. Agrawal and M. Srikant, “Fast algorithms for mining association rules in large databases [R],” IBM Almaden Research Center, Tech Rep: RJ9839, 1994.
[4] J. W. Han, J. Pei, Y. W. Yin, et al., “Mining frequent patterns without candidate generation: A frequent-pattern tree approach [J],” Data Mining and Knowledge Discovery, Vol. 8, No. 1, pp. 53–87, 2004.
[5] F. V. Jensen, “An introduction to Bayesian networks,” Springer, New York, 1996.
[6] M. desJarins, “Representing and reasoning with probabilistic knowledge: A Bayesian approach,” Uncertainty in Artificial Intelligence, pp. 227–234.
[7] N. Friedman, D. Geiger, and M. Goldszmidt, “Bayesian network classifiers,” Machine Learning, pp.131–163, 1997.
[8] G. Cooper and E. Herskovits, “A Bayesian method for the induction of probabilistic networks from data [D],” Machine Learning, Vol. 9, No. 4, pp. 309–347, 1992.

