Int'l J. of Communications, Network and System Sciences
Vol.2 No.6(2009), Article ID:694,7 pages DOI:10.4236/ijcns.2009.26056
Two-Dwell Synchronization Techniques and Mimo Systems for Performance Improvements of 3G Mobile Communications
Digital Signal Processing, Multimedia, and Optical Communications Laboratory, Department of Applied Electronics University of ROMA TRE, Rome, Italy
Email: fbenedet@uniroma3.it
Received April 20, 2009; revised June 3, 2009; accepted July 29, 2009
Keywords: Initial Code Acquisition and Synchronization, MIMO Systems, Probability Tests, Sptio-Temporal Signal Processing, Mobile Communications
ABSTRACT
This paper considers the case of smart antennas and multiple inputs multiple outputs (MIMO) systems, suited for the radio access of 3G mobile communications, involving two-dimensional spatio-temporal signal processing and two-dwell procedures. The main novelty of our work is twofold: first, a two-dwell acquisition technique is here performed to save the mean acquisition time versus one-dwell acquisition techniques; second, the searching procedure is driven from the estimates of the local signal-to-interference-plus-noise ratio, reducing again the mean acquisition time. Some examples of application to the detection of 3G communication signals in typical mobile scenarios are provided and we have verified the effectiveness of the analyzed spatio-temporal two-dwell procedures. The presented technique seems to constitute a promising tool for analytic setting of near optimum spatio-temporal acquisition testing procedures based on serial search/verification modes.
1. Introduction
Direct-Sequence Spread-Spectrum Code-Division Multiple-Access (DS/SS CDMA) has raised a significant importance in mobile communications of the last few years [1]. It has emerged as the incoming standard for third-generation radio-mobile transmission technology [2], since it offers significant advantages in terms of channel capacity, mobile power consumption, link quality and resilience to multi-path propagation [3]. However, in order to exploit the advantages of a DS/SS signal in a CDMA system, receivers must first be able to synchronize the local pseudo-noise (PN) code with the incoming PN code [4,5]. Usually, the problem is solved via a two-step approach: first an initial code acquisition, which synchronizes the transmitter and receiver to within an uncertainty of a chip period, is realized; second, a code tracking phase, which performs and maintains fine synchronization between transmitter and receiver, is carried out [4].
Synchronization process in Wideband Code-Division Multiple-Access (W-CDMA) [2] (i.e. the process in which the mobile station searches for cell and scrambling codes and their timing) consists of five sequential steps: 1) slot synchronization, 2) frame synchronization and scrambling code group identification, 3) scrambling code identification, 4) frequency acquisition, and 5) cell identification. This contribution addresses algorithms for the initial cell search consisting of slot synchronization (i.e. the first stage), under a possible systematic frequency error. The combined goal of such stages is to deliver a reliable code-time candidate to the frequency acquisition stage.
The process of searching for a cell and synchronizing to its downlink scrambling code is often referred to as cell search [2]. Cell search is necessary after the mobile station has switched on (initial search), and during idle and active modes, for identifying new camping cells or handover candidates, respectively. Idle and active mode search is also called target cell search. The performance of cell search impacts the perceived switch-on delay (initial search), stand-by time (idle mode search), and link quality (active mode search), and thus is important to mobile station design.
Conventional initial acquisition methods in the radio access of third generation (3G) mobile communications are based on serial multi-dwell hypothesis tests, based on non-coherent correlation from a number of data blocks. The test sequentially searches for the most likely codes and their optimum timing shift as reliable candidates for code (and code offset) acquisition [2,6]. The constant false alarm rate (CFAR) criterion, often employed to perform effective tests [7], is adopted to determine the threshold value.
This work considers the case of smart antennas and multiple inputs multiple outputs (MIMO) systems, suited for the radio access of 3G mobile communications [8,9]. The presented technique involves twodimensional (2D) spatio-temporal signal processing and two-dwell procedures. The main novelty of the presented procedure is twofold: first, a two-dwell acquisition technique is here performed to save the mean acquisition time respect to one-dwell acquisition techniques; second, the searching procedure is driven from the estimates of the local signal-to-interference-plus-noise ratio (SINR), reducing again the mean acquisition time.
This paper is organized as follows. In Section 2, the basic outlines of two-dwell non-coherent code acquisition techniques are presented, while in Section 3 the analysis is extended to the case of smart antennas and MIMO systems, involving 2D spatio-temporal signal processing. In particular, we preliminary discuss on the spatial coverage of the customers, assuming an adaptive management of call admission from distinct angular sectors. Section 4 shows the analytic performance expressed by using the Generalized-Q (GQ) functions, and provides application to typical mobile operating scenarios. The conclusions of the paper are finally drawn in Section 5.
2. Frameworks of Two-Dwell Non-Coherent Acquisition
The two opposite cases of acquired or mismatched code offset are often referred to as in-sync and out-of-sync conditions. These cases differ because the output of a matched filter is ideally constant in the former condition, while it randomly varies in the latter one. In fact, it is well known that the user codes employed are orthogonal only if the users are chip-synchronized with each other. In practice, any pair of codes may present a relevant cross-correlation for nonzero chip offset. Such a residual correlation acts as a random variable (the codes are usually modulated by independent data streams), characterized by a noise-plus-interference variance depending on the effective time synchronization. Testing for the presence of useful signal should discriminate over the following two hypotheses:
- H1: presence of signal, in-sync case;
- H0: absence of signal, out-of-sync case.
Hence, the multi-dwell sequential testing procedure [10,11] must decide on the presence (H1 hypothesis) or absence (H0 hypothesis) of useful signal from a set of 0 testing variables (N=number of dwells, being N = 2 in the application presented herein). The H1 hypothesis is accepted if all the testing variables exceed a corresponding set of N thresholds. Conversely, if one (at least) of the N variables assumes a lower value, the H1 hypothesis is rejected. In practice, the fairly frequent H0 hypothesis can be detected in a quicker time from the test of few variables. This usually reduces the overall mean decision (signal acquisition) time.
The N testing variables consist of the complex correlator outputs r1 … r2 … rN, taken at N different times, between a given number of samples of each reference signal and the received signal, which is assumed to be corrupted by additive independent Gaussian noise. In fact, a large number of samples is required in presence of very low signals, such as in the case of the spreadspectrum systems that need large processing gains. In such cases, the Gaussian model is asymptotically valid, as consequence of the central limit theorem. Therefore, the correlator output is usually assumed to be a non-zero mean (H1 hypothesis) or zero mean (H0 hypothesis) Gaussian complex variables.
Past attempts considered the case of independent data blocks for sake of simplicity. Conversely, it has been shown that performance improves while serial tests based on correlation magnitude of overlapping data blocks are taken into account [11]. The performance of the whole system, expressed in terms of the probabilities of detection and false alarm, have been extensively computed and analysed [11], achieving a further performance optimisation in [12]. A closed form solution to the mathematical problem of determining the error probabilities (as a function of Bessel functions) was also therein addressed by the definition of the generalized-Q (GQ) functions (generalizing the Marcum’s Q-functions).
For N=2, the probabilities of false alarm and detection (Pf and Pd) obtained by testing the correlation magnitudes |r1| and |r2| measured over the (overlapped) data block with respective lengths L1 and L2, can be expressed by the GQ-functions [11,12], that also depend on the respective testing thresholds V1 and V2:
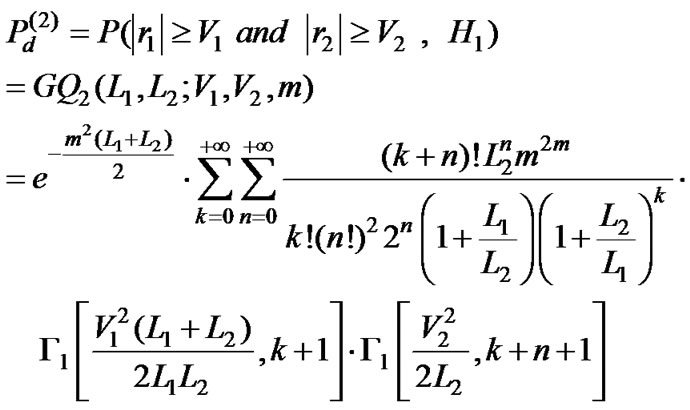 (1)
(1)
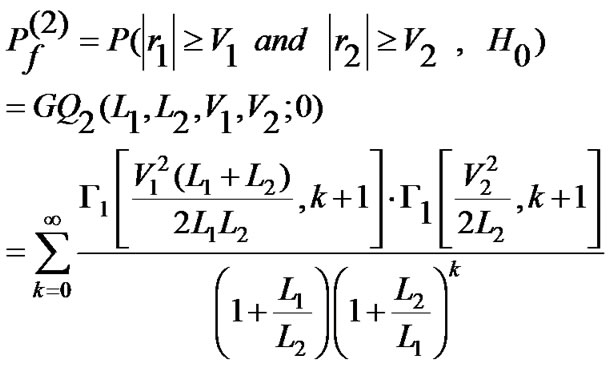 (2)
(2)
having defined the complement to one of the incomplete gamma function as [11,12]:
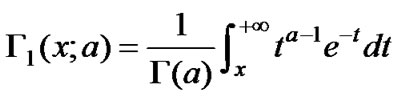 (3)
(3)
In such a case, optimum test design consists in the minimization of the mean acquisition time for a given number of cells and constant probabilities of detection Pd, false-alarm Pf, and a penalty time TP following a false-alarm decision. Adoption of the optimal set of parameters in the acquisition test can lead to a further significant reduction of the mean duration of sequential tests [12]. Standard numerical algorithms, such as the steepest descent or the Newton-Raphson’s, can determine the optimal set.
In the two-dwell case (sometimes named as search and verification modes), the mathematical problem consists of searching for the set of the optimum values of four parameters (i.e. two time durations L1, L2 of the tests and the corresponding two threshold values V1, V2) that minimize the function mean acquisition time, under two constraints (i.e. the desired error probabilities Pd and Pf). It is interesting to observe that this will minimize the standard deviation of the acquisition time too [10].
3. Two-Dimensional Two-Dwell Spread-Spectrum Code Acquisition
In our analysis we have used the Constant False Alarm Rate (CFAR) procedure, often employed to perform effective tests [7]. In particular, the CFAR test is accomplished in two successive parts: first, a threshold is determined to limit the false-alarm probability Pf at a given reduced value (also named size of the test); second, the probability of detection Pd (also named power of the test) is evaluated for the threshold previously determined [13]. The probability of false alarm must be tuned to guarantee a very low number of possible false alarms, which eventually imply a relevant penalty time to the acquisition device. Large probabilities of detection (up to 100%) are typical of well-performing testing variables [10,11].
Starting from the one-dwell approach of Katz and Glisic [8,9], we exploit the capabilities of spatio-temporal search when two-dwell algorithms are employed. Also in such a case, the GQ-functions represent a very useful tool to express the performance in an analytic form also in the two-dimensional case.
The mean code acquisition time of the test for the single cell is well approximate by [10]:
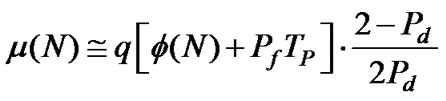 (4)
(4)
where TP represents the penalty time for a false alarm decision that implies a very time consuming acquisition system reset [11], while:
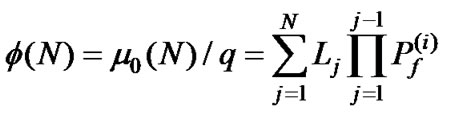 (5)
(5)
and, in particular, for N = 2:
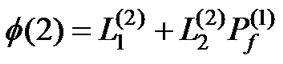 (6)
(6)
From the analysis of the GQ-function of the second order (GQ2), we obtain the important theoretical relationship assuming the constant testing probabilities Pd(2) and Pf(2):
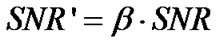 (7)
(7)
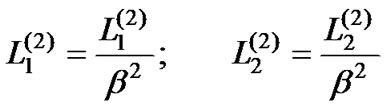 (8)
(8)
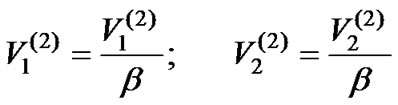 (9)
(9)
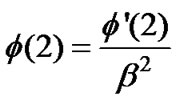 (10)
(10)
The same procedure can apply to the problem of sequential cell acquisition, after defining the concept of angular cell following the approach of [8,9]. In such a case, the spatial cells are directionally scanned by means of the antenna array. Each cell covers a given angular sector. It can possibly vary according to the employed procedure. Moreover, the distribution of noise and noise-like interfering users may vary versus the angle itself.
The choice of the width of the angular sectors (examined in the following) is critical since narrowing the beam increases the detection probability in the delay-angle cell that actually contains the signal, while the effective signal-to-interference-plus-noise ratio (SINR) becomes higher. But, in the meanwhile, it can lead to a higher overall mean acquisition time, because, for a given uncertainty, it also implies an increase in the number of sectors to be tested.
Defining H1,i and H0,i as the hypotheses that the system decides that the signal is present or not (with the tested code and time offset) in the i-th cell, being S1,i and S0,i the hypotheses that the tested signal candidate is actually present or not in the i-th cell, their respective probabilities are:
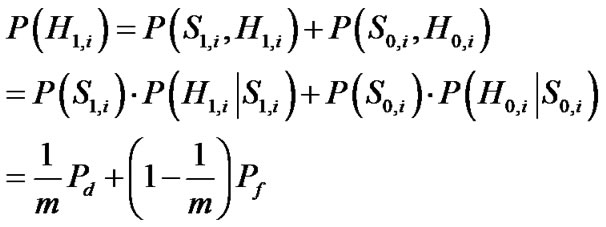 (11)
(11)
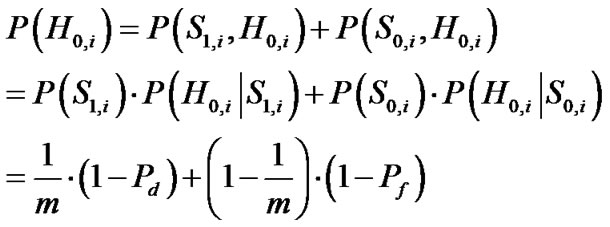 (12)
(12)
The total mean acquisition time TOT for searching over an ensemble of m possible cells is expressed as:
 (13)
(13)
where the terms {m1, m2, m3 …} include the penalty factors of their corresponding sectors. The sum extends till m if only one round of search is implemented, i.e.:
 (14)
(14)
If a number g of search cycles are implemented, the upper limit (formerly the sector number m) of the two sums in the above equation becomes m•g. It may even go to infinite (with a probability that tends to zero) if a no-stop search (g→+∞) is considered, that is:
 (15)
(15)
where the sector indices i, j, and k are now evaluated modulus m (respectively denoted as i]m, j]m, and k]m).
Let us observe that when the probabilities P(H1,i), P(H0,i) and the acquisition times are the same in the various sectors (i.e. P(H1,i) = a and P(H0,i) = 1-a, and mi = m) the overall mean acquisition time reduces to:
 (16)
(16)
4. Results and Discussion
In this section, we aim to show through a wide number of simulation trials the effectiveness of the previously analyzed spatio-temporal two-dwell technique, providing application to typical mobile operating scenarios. We present the performance of the new scheme in terms of overall acquisition time, μTOT, and signal-to-interference plus noise ratio (SINR) varying the number m of angular sectors as well as the number g of full scans of all the sectors.
Some examples of application to the detection of direct-sequence spread-spectrum communication signals are provided. In particular, we are assuming an adaptive management of call admission control based on a uniform a priori probability of the (possibly non-uniform) angular sectors. In such a target case, the spatial coverage of the customers is optimized. The effect of a random (non-ideal) distribution of users is then considered in all the following analyses. Assuming that no information is available on the a priori distribution of user signals, two strategies of call search may be thought, namely random and SINR-ordered. In fact, beginning the search from the highest SINR cells till the lowest SINR ones reduces the mean acquisition time. In actual environments, the measured SINR value accounts for the number of interfering users, regarded as noise-like independent disturbs.
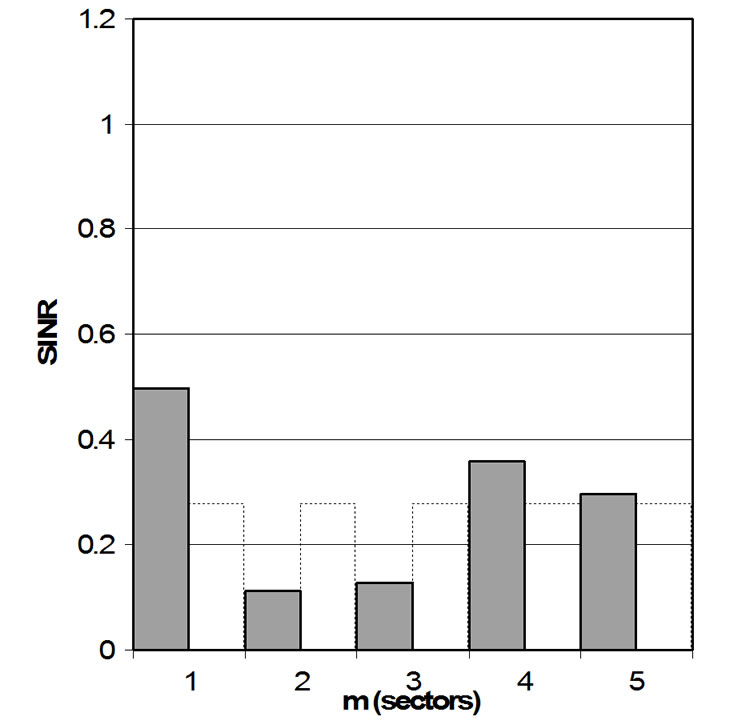
In particular, Figure 1 shows two possible cases of uniformly distributed interference plus noise in m = 5 (Figure 1(a)) or 10 (Figure 1(b)) angular sectors. The SINR directly represents the ratio between the useful synchronization signal power and the interferenceplus-noise power (measured at the input of a receiver) on a linear scale (not in dB). For a proper matching, we have assumed that the same total signal and interference-plus-noise powers over the ensemble of all the sectors in all the examined cases. The equivalent constant distribution of interferenceplus-noise is shown in dashed lines for a visual comparison. In such a case, the SINR (considering both thermal noise and noise-like interference) of each angular cell increases proportionally to the number of considered sectors.
In particular, we have examined three reference cases, respectively taken from Tables 2, 3, and 4 of [11] (also used for numerical comparison in [12]). We have varied the number of circular sectors (m = 1…10), all of them characterized by uniform random distribution of interference plus noise. The overall acquisition time μTOT is depicted in the Figures 2(a)–(c) versus the chosen number m of sectors.
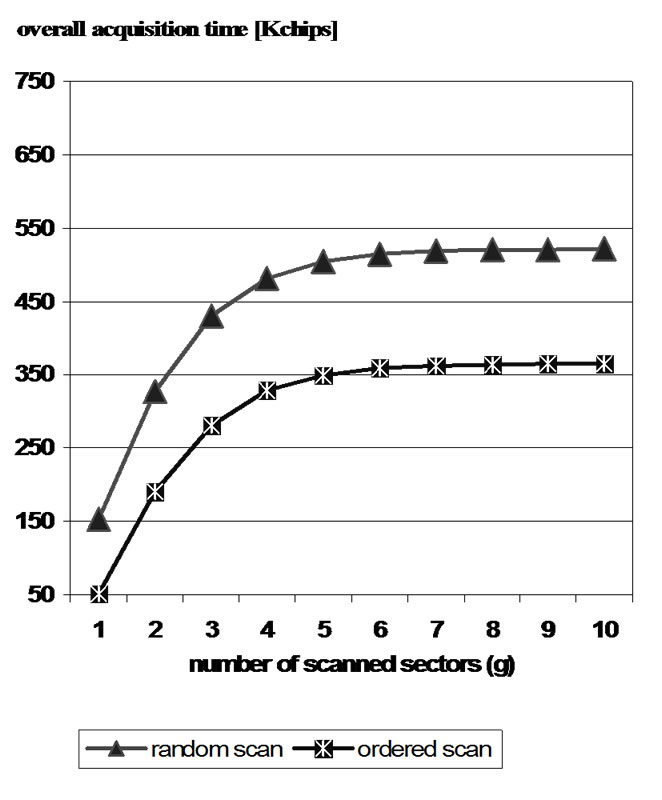
Moreover, the obtained overall acquisition time μTOT is plot in Figure 3 versus the number of sector scans (g), for m = 3 (Figure 3(a)) and 10 (Figure 3(b)) total sectors respectively, assuming the uniform random distribution of interference plus noise. In both the cases, the limit value (g→+∞) is well approximated for g ≥ 6 search cycles. The overall acquisition time μTOT is finally depicted in the Figure 4 versus the chosen number m of sectors, for a large number g of search cycles (g = 10 were used here). It can be seen that a number m ≥ 7 of spatial sectors may be a valid compromise, in the examined example, between the high performance allowed by focusing techniques and the
 (a)
(a) 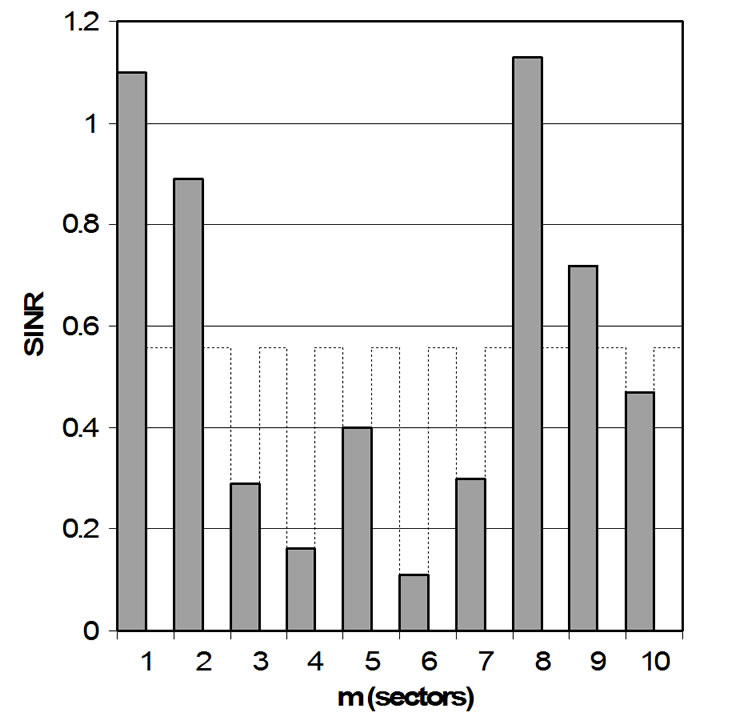 (b)
(b)
Figure 1. A uniform realization of random interference plus noise (SINR) in 5 angular sectors (left) and in 10 angular sectors (right).
 (a)
(a) 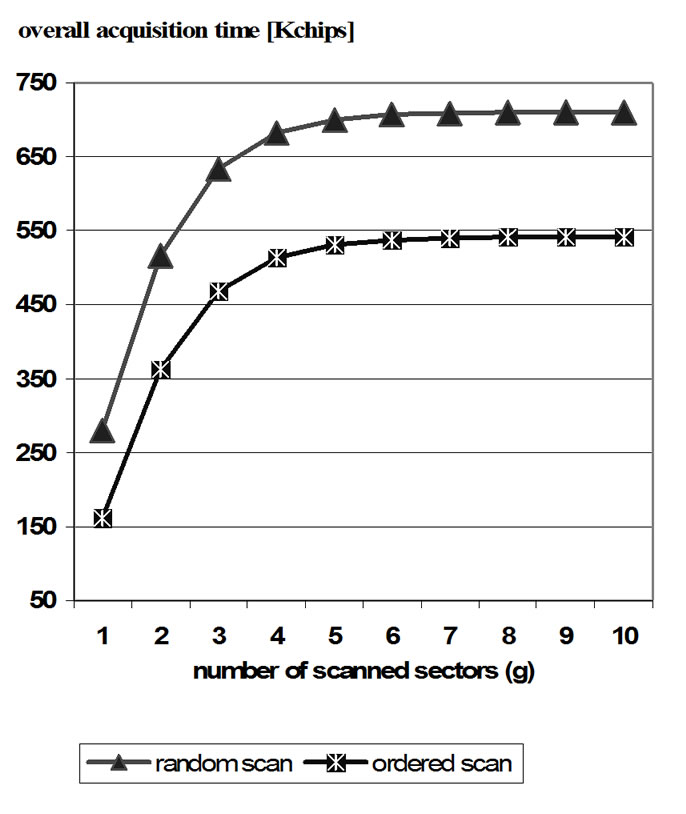 (b)
(b)
Figure 2. The obtained overall acquisition time versus the number of sector scans (g) for m = 3 (left) and for m = 10 (right) total sectors assuming the uniform random distribution of interference plus noise.
system complexity in terms of both operating apparatus and computation cost of signal processing.
Therefore, the main novelty of the presented approach is twofold: first, a two-dwell acquisition technique is here performed to save the mean acquisition time respect to one-dwell acquisition techniques;second, the searching procedure is driven from the estimates of the local signal-to-I nterference-plusnoise ratio (SINR), reducing again the mean acquisition time. The obtained results evidence the effectiveness of the analyzed spatio-temporal two-dwell procedures.
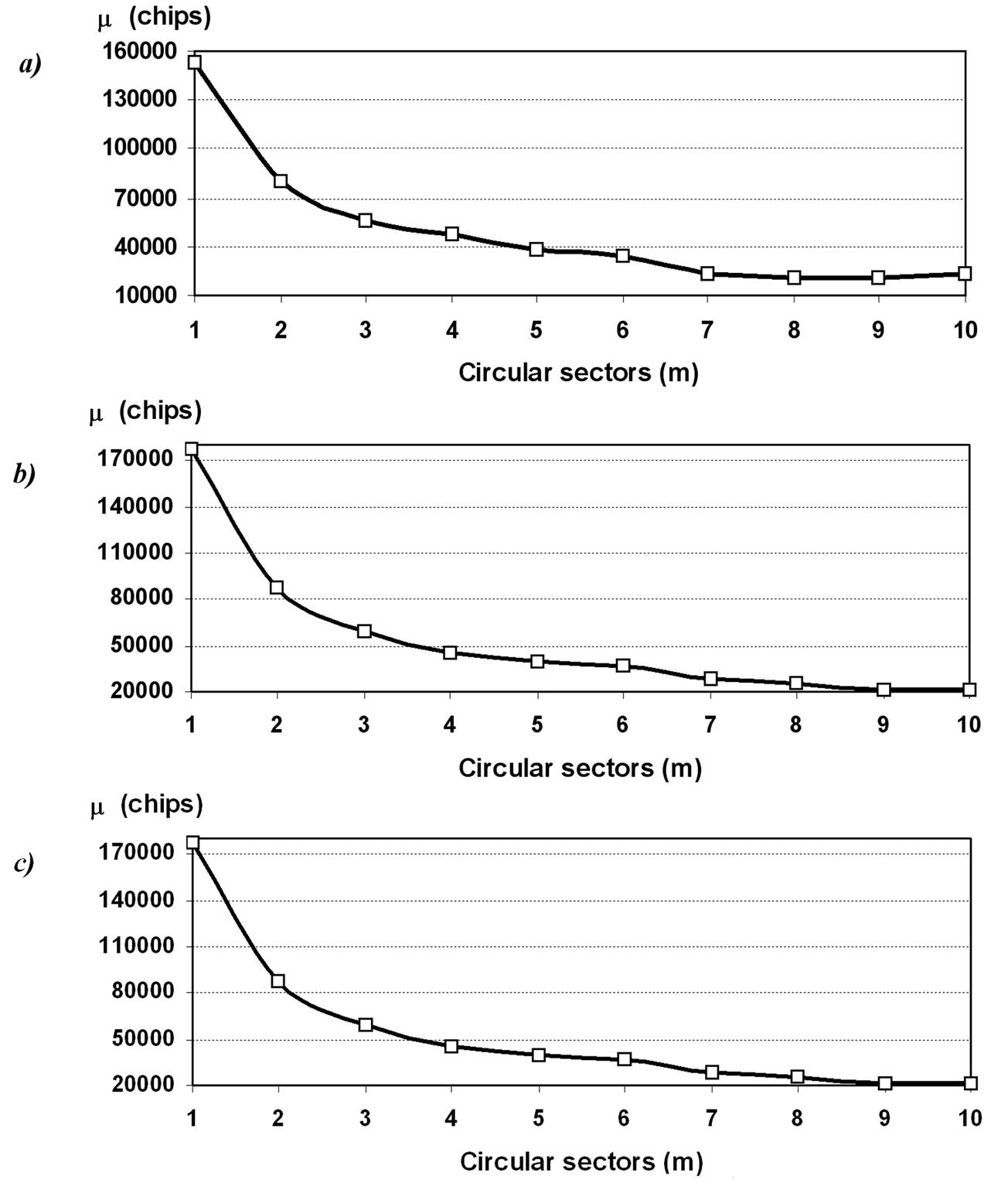
Figure 3. Overall acquisition time versus the number m of sectors (for large g) in the first reference case: (a) Table 2, (b) Table 3, (c) Table 4 of [6] (SINR = -18 dB per chip; q = 63; Pd = 0.99; Pf =0.0001) assuming uniform random distribution of interference plus noise.
5. Conclusions
This paper extends the analysis of two-dwell procedures (search /verification modes) to the spatial domain for the initial code synchronization of 3G mobile communications. We showed that also in this case the GQ functions may represent a useful tool to express the performance in an analytic form, as well in the two-dimensional case. From the technical viewpoint, a two-dwell acquisition technique is here performed to save the mean acquisition time respect to one-dwell acquisition techniques. Two searching strategies (ordered and random respect to the measured SINR) have been considered and implemented. Some examples of application to the detection of DS/SS communication signals in typical mobile scenarios are provided and we have verified the effectiveness of the analyzed spatio-temporal two-dwell procedures.
The presented technique seems to constitute a promising tool for analytic setting of near optimum spatiotemporal acquisition testing procedures based on serial search/verification modes.
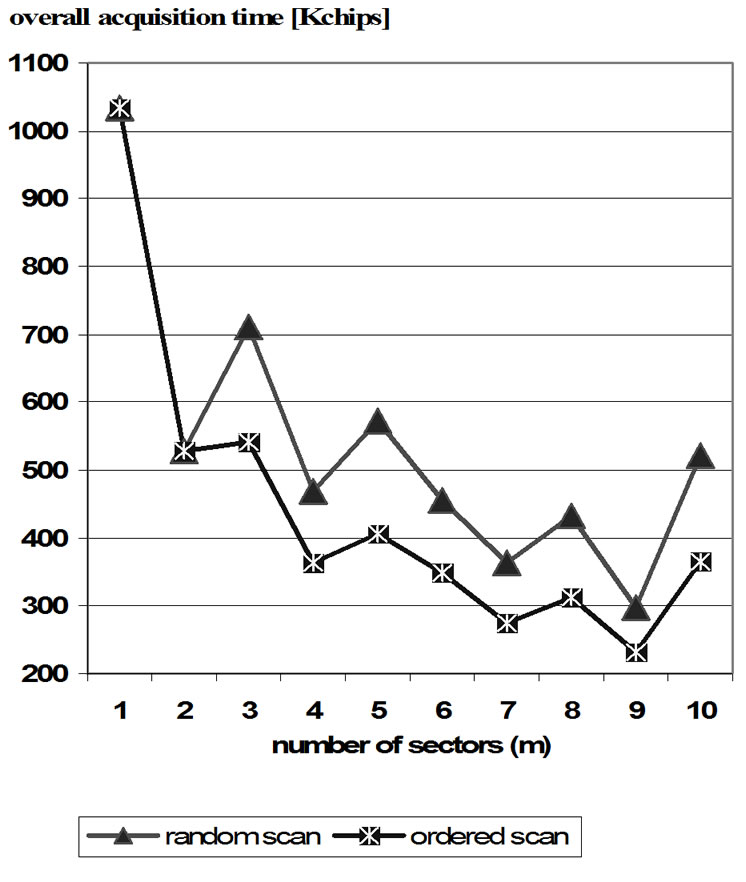
Figure 4. The obtained overall acquisition time versus the number m of sectors for a large number g of search cycles assuming the uniform random distribution of interference plus noise.
6. Acknowledgement
The authors wish to thank Prof. A. Neri of the University of Roma Tre for his helpful discussions on application to 3G Mobile Systems.
7. References
[1] R. L. Pickholtz, L. B. Milstein, and D. L. Schilling, “Spread spectrum for mobile communications,” IEEE Transactions on Vehicular Technology, Vol. 40, pp. 313–322, February 1991.
[2] Y. P. E. Wang and T. Ottosson, “Cell search in W-CDMA,” IEEE Journal on Selected Areas in Communications, Vol. 18, No. 8, August 2000.
[3] R. Esmailzadeh and M. Nakagawa, “Pre-rake diversity combination for direct sequence spread spectrum mobile communications systems,” IEICE Transactions on Communications, pp. 1008–1015, August 1993.
[4] Y. H. Lee and S. Tantaratana, “Sequential acquisition of PN sequences for DS/SS communications: Design and performance,” IEEE Journal on Selected Areas in Communications, Vol.10, pp. 750–759, May 1992.
[5] S. Tantaratana, A.W. Lam, and P. J. Vincent, “Noncoherent sequential acquisition of PN sequences for DS/SS communication with/without channel fading,” IEEE Transactions on Communications, Vol. 43, pp. 1738–1746, 1995.
[6] J. C. Lin, “Noncoherent sequential PN code acquisition using sliding correlation for chip-asynchronous direct-sequence spread-spectrum communications,” IEEE Transactions on Communications, Vol. 50, No. 4, pp. 664–676, April 2002.
[7] E. Moulines and K. Choukri, “Time-domain procedures for testing that a stationary time series is Gaussian,” IEEE Transactions on Signal Processing, Vol. 44, pp. 2010–2025, August 1996.
[8] M. Katz and S. Glisic, “Two approaches for enhancing performance of two-dimensional code acquisition in spatially nonuniform interference environments,” in Proceedings of International Conference on Wireless Personal Multimedia Communications, WPMC’01, Aalborg, Denmark, pp. 1071–1076, September 2001.
[9] M. Katz, J. Iinatti, and S. Glisic, “Search strategies for two-dimensional code acquisition in environments with non-uniform spatial distribution of interference,” in Proceedings International IEEE Vehicular Technology Conference, VTC 2001 Spring, IEEE VTS 53rd, Vol. 2, pp. 1454–1458, 2001.
[10] D. M. Di Carlo and C. L. Weber, “Multiple dwell serial search: Performance and application to directsequence code acquisition,” IEEE Transactions on Communications, Vol. 31, pp. 650–659, May 1983.
[11] G. Giunta, “Generalized Q-functions for application to non-coherent serial detection of spread-spectrum communication signals,” IEEE Transactions on Signal Processing, Vol. SP-48, No. 5, pp. 1506–1513, May 2000.
[12] G. Giunta, A. Neri, and M. Carli, “Constrained optimization of non-coherent serial acquisition of spreadspectrum code by exploiting the generalized Q-functions,” IEEE Transactions on Vehicular Technology, pp. 1378–1385, September 2003.
[13] G. Giunta and L. Vandendorpe, “A ‘Rayleighness’ test for DS/SS code acquisition,” IEEE Transactions on Communications, Vol. 51, No. 9, pp. 1492–1501, September 2003.

