Journal of Intelligent Learning Systems and Applications
Vol.4 No.1(2012), Article ID:17559,11 pages DOI:10.4236/jilsa.2012.41007
An Improved Genetic Algorithm for Crew Pairing Optimization
![]()
Faculty of Aeronautics and Astronautics, Istanbul Technical University, Istanbul, Turkey.
Email: bzeren@gmail.com, ozkol@itu.edu.tr
Received July 23rd, 2011; revised December 27th, 2011; accepted January 6th, 2012
Keywords: Optimization; Genetic Algorithms; Crew Planning; Crew Pairing; Crew Pairing Optimization; Airline Crew Planning; Airline Crew Pairing; Airline Crew Pairing Optimization
ABSTRACT
Crew pairing is a sequence of flights beginning and ending at the same crewbase. Crew pairing planning is one of the primary processes in airline crew scheduling; it is also the primary cost-determining phase in airline crew scheduling. Optimizing crew pairings in an airline timetable helps minimize operational crew costs and maximize crew utilization. There are numerous restrictions that must be considered and just as many regulations that must be satisfied in crew pairing generation. The most important regulations—and the ones that make crew pairing planning a highly constrained optimization problem—are the the limits of the flight and the duty periods. Keeping these restrictions and regulations in mind, the main goal of the optimization is the generation of low cost sets of valid crew pairings which cover all flights in the airline’s timetable. For this research study, We examined studies about crew pairing optimization and used these previously existing methods of crew pairing to develop a new solution of the crew pairing problem using genetic algorithms. As part of the study we created a new genetic operator—called perturbation operator. Unlike traditional genetic algorithm implementations, this new perturbation operator provides much more stable results, an obvious increase in the convergence rate, and takes into account the existence of multiple crewbases.
1. Introduction
Airline crew scheduling is defined as process of assigning crew members with a variety of flight qualifications to flight duties to ensure all flights in an airline’s timetable are properly covered by the crew. The importance of optimum crew scheduling cannot be overstated as all airlines operate in a very complex environment. In addition, with increasing competitiveness in the marketplace, airline companies are in a position to better manage their expenses using effective flight scheduling techniques. Additionally, crew costs are second only to fuel costs in terms of operational costs.
Airline crew scheduling problems include different NPComplete (non-deterministic polynominal) and combinatorial subproblems. For instance, crew pairing can consist of millions of different combinations since a medium sized airline company might have hundreds of different connections at an airport.
There are two different strategies used to solve crew scheduling problems. First, one solves the problem in just one phase (Crew pairing and crew rostering together) like in references [1] and [2]. However, the requirement of high calculation capabilities and an overlarge search space, reduces the probability of generating a feasible solution using an optimization algorithm.
The second strategy is based on solving the problem in two phases. These phases are crew pairing and crew rostering. In this approach, the crew pairing problem is solved first. Crew pairing sets are generated that cover all flight legs in the airline’s timetable. Next the crew rostering problem is solved. In this second phase, the crew assignment is carried out for each crew pairing in the crew pairing sets. There are many constraints inherent in both of these phases, all implemented by Directorate General of Civil Aviation [3] or the airline company itself. This situation turns the problems into highly constrained optimization problems.
Genetic algorithms can be understood as an intelligentprobabilistic search algorithm which can be applied to a variety of combinatorial optimization problems [4]. Theoretical foundations of genetic algorithms were developed by Holland J. [5] with the inspiration of the evolutionary process seen in nature. During the evolutionary progress, the population of solutions evolves according to principles of natural selection. In the population, better adapted individuals have a higher probablity of survival than others, and less fit individuals are eliminated. In this way, during the evolutionary process, the genes (genetic information) of individuals of good quality are transfered to new generations. Gene combinations of individuals of good quality may yield more fit individuals than themselves thus individuals of better quality can be produced during the evolution process.
Genetic algorithms simulate this evolutionary optimization process by applying genetic operators in the first generation which is produced randomly in following generations. Every individual in the population expresses a possible solution that is specific to the problem and is represented through chromosomes. Fitness value of every chromosome is calculated by the fitness (objective) function which is used. Individuals of good quality transfer their genetic information to new generations with a reproduction process which is implemented by crossover operator with other individuals of good quality. In this way, genetic information from the parents is transferred to child generations and new solutions are generated permanently. Mutation operator is applied with a small probablity on child chromosomes of every generation by changing some genes on them to avoid premature convergence. Finally, either child generation is replaced with old generation (generational approach) or individuals of good quality in the child generation are replaced with individuals of low quality in the old generation (steadystate approach). The whole process is repeated until a satisfactory solution was found.
2. Related Works
The crew pairing optimization problem constitutes the main focus of this study. The main goal of crew pairing optimization is the minimization of crew costs of an airline company via searching optimized crew duty schedules. All crew member data resides at a crewbase and the crew pairings have to begin and end at these crewbases.
Generally the crew pairing problem is solved in two phases. First, an enormous number of legal crew pairings are generated for each crewbase. To generate crew pairings, airlines use either column generation based methods (as seen in reference [6]) or iterative tree search algorithms (as seen in reference [7]). Column generation based methods generate crew pairings during optimization in progress. In this method, they mainly divide the whole problem into two separable (master and sub problem) problems designed to produce high-quality solutions. This becomes a problem is the data base is too big which generates huge columns and constraint matrices and become computationally much more expensive compared to probablistic intelligent methods like genetic algorithms.
The issue of these exact methods make implementation of genetic algorithms more interesting. Nevertheless, implementing a column generation approach to huge integer programming problems (as seen in reference [8]) should be considered in an attempt to evaluate the quality of genetic algorithm solutions. A method which was developed in reference [9] for abnormally large problems based on random pair generation with dept-first search algorithm can be applied.
In this study, dept-first search method is used to generate crew pairings (like those in reference [7]). In the second phase, the optimization process is completed. In this phase the best subset of generated crew pairings are searched and selected. The goal of this phase is to minimize crew costs and to cover all flights in the timetable of the airline. The crew pairing optimization problem is mostly modeled as a set-covering problem. Set-covering problems can be solved by using branch and bound or genetic algorithms based methods. Branch and bound based methods use highly complex and time consuming calculations. This makes it difficult in very large set-covering problems. But genetic algorithms use an intelligent probabilistic search mechanism. This feature allows them to search a much larger search space in less time.
Different genetic algorithm implementations were developed to solve set-covering problems. As noted in reference [4], Beasley and Chu used column based chromosomes, variable mutation rate, and a heuristic mechanism to repair chromosomes to solve the problem. In reference [7], Kornilakis and Stamatopoulos developed a crew pairing algorithm based on reference [4] and reported good results. And in reference [10], a row-based representation is used to solve a set-covering problem but the representation technique and operators used in this study make it difficult to cope with unfeasible chromosomes. In study [11], another a row based model is proposed to solve the problem. This approach has given good results but it is based on a strong heuristic mechanism using select appropriate colums according to the order of rows in a chromosome. There are also similar applications (as shown in study [12]) which use a special chromosome design. The idea they use is to keep the diversity of genes in chromosomes as high as possible by adding an unexpressed part to them. In this study this method was also applied to the crew pairing problem with small modifications and results can be seen in the experimental results section.
Because of the probabilistic nature of the genetic algorithms it is not possible to guarantee finding global optimum. Mutation operator becomes too important to avoid getting stuck in local minima. In reference [4] a variable mutation rate is proposed. In the presented study variable mutation rate is also implemented in a similar way. Additionally, adaptation and application of perturbation operator to crew scheduling problem and multibase approach can be considered the main improvement of this study.
Perturbation operator technique is a local search method used after the repair of a chromosome. This operator should not be used in every genetic iteration because of the issue of premature convergence. As can be seen in the experimental results section, the perturbation operator increases the convergence rate; it is approximately three times faster. Though the total calculations take more time compared to the cases without perturbation operator run, by using this approach the best cost values of genetic algorithm runs without perturbation operator is obtained in very early iterations. Another important point that must be mentioned is the multibase crew pairing solution. The crew pairing generation phase, optimization phase, and more importantly, fitness function is modified to implement a multibase crew pairing solution.
Genetic Algorithms is also widely used in other airline scheduling and optimization problems. A good study on flight scheduling can be seen in reference study [13].
3. Fundamental Definitions and Concepts in Airline Crew Scheduling
In this section some of the main definitions and constraints about crew pairings are outlined. These are either identified by government regulations or airline company agreements.
3.1. Flight Duty
A flight duty is the time period consisting of one or more flight(s). There is always a specific preparation period before the first flight’s departure and an end period after the last flight’s arrival. These preparation and end periods are also determined by regulations. After the end of a flight duty, the crew must have a predefined rest period. A sample flight duty with four flights is depicted in Table 1.
Duration of flight duties constitutes one of the fundamental constraints in the airline crew scheduling process and is limited by regulations. All flight duties generated in the flight duty generation phase must fit the Crew and Duty Regulations of Directorate General of Civil Aviation [3]. The maximum duration time of a flight duty depends on the range of flights it contains, implemented crew model (time period might be increased with crew augmentation), and number of landings. The time periods of normal and extended range flight duties can be seen in Tables 2 and 3 [3]. According to the regulations, for a flight duty to be accepted as an extended range flight duty, 4 hours of time slice or 8 hours of flight time must be passed.
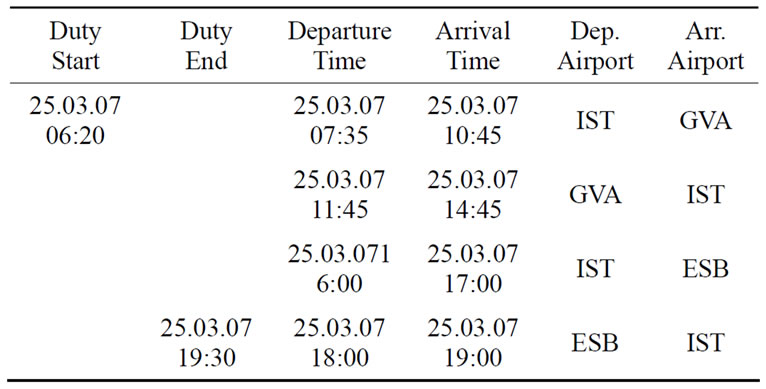
Table 1. Sample flight duty.

Table 2. Maximum duration of normal flight duty.

Table 3. Maximum duration of normal flight duties.
3.2. Rest Period
Rest period is the time period that starts after a flight duty and crew would be free for all kind of duty when they were in. The minimum duration of rest periods are showed in Table 4 [3].
3.3. Crew Pairing
A crew pairing is a sequence of flights which begins and ends at a particular crewbase and consists of one or more flight duty(s). Unlike flight duties, crew pairings include rest periods. According to the regulations, a crew member cannot be away more than 10 days [3]. Therefore a crew pairing cannot last more than 10 days. A sample crew pairing which consists of two flight duties and four flights can be seen in Table 5.
3.4. Dead-Head Flight
If a crew member flies as a passenger instead of as a cockpit or as a cabin attendant, this flight is called as dead-head flight for that crew member. Dead-head flight is a factor that reduces passenger transport capacity and efficiency of crew utilization. Therefore minimization of the number of dead-head flights is always desirable in the scheduling process. Dead-head flights are encountered
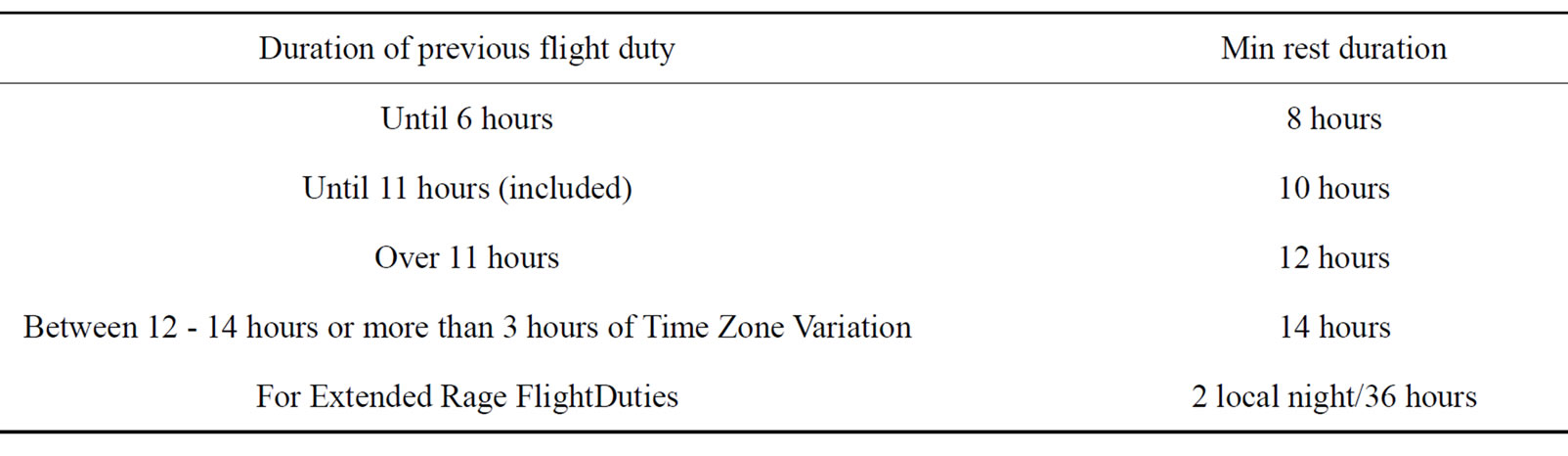
Table 4. Minimum duration of rest periods.
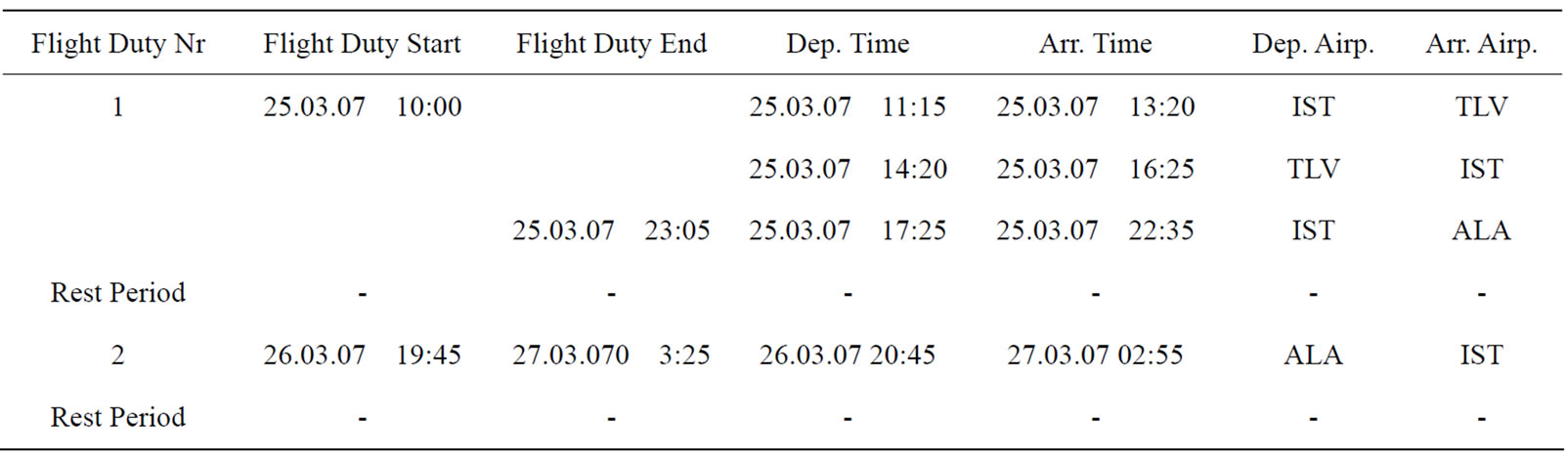
Table 5. Sample crew pairing.
when there is a crew member who has to fly to another airport to complete a flight which starts from that airport.
4. Solution of Crew Pairing Problem
Generally, the crew pairing problem is solved in two phases because of the large size of search space (as can be seen in references [6] and [7]), and the constraints which convert the problem to a highly constrained nonlinear optimization problem and objective function are satisfied.
1) Crew pairing generation: In this phase, many legal crew pairings are generated using the airline’s timetable; for each crew pairing necessary values are carried out that will be used in calculating the objective function. There are some constraints that must be taken into account for crew pairings to be considered legal crew pairings. While some of these constraints are spatial and temporal constraints, the rest of them are originated from Crew and Duty Regulations of Directorate General of Civil Aviation [3] or special implementations of the airline company itself.
2) Optimization: Among crew pairings generated in the previous phase, subsets of crew pairings are searched which minimize crew costs and cover all flights in the schedule at least once (over-covering indicates dead-head flights).
The advantage of this approach is that the constraints are taken into account only during the first phase. Therefore the optimization becomes independent of constraints. In fact, once a large-size set of legal pairings has been generated, the second phase can be modelled as a set covering problem, a widely known combinatorial optimization problem [7].
4.1. Crew Pairing Generation
Input data of the crew pairing generation process is the set of flightsFwhich is taken from airline flight schedule. System constraints are defined as a function 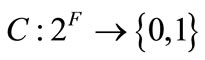 . Here crew pairing p is a legal crew pairing if
. Here crew pairing p is a legal crew pairing if 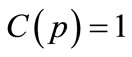 and is not legal if
and is not legal if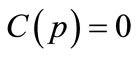 . The purpose of this phase is to obtain a set of all feasible crew pairings
. The purpose of this phase is to obtain a set of all feasible crew pairings 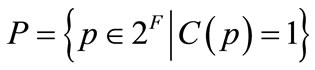 [7].
[7].
Considering the size of the problem however, it is not efficient nor is it possible to enumerate all feasible crew pairings. For instance if  then it requires 21000 crew pairings be evaluated. At the same time, generation of too many crew pairings naturally increases the difficulty of the optimization phase. Therefore, in this phase as few crew pairings as possible are generated which allows preservation of the robustness and the quality of the solution.
then it requires 21000 crew pairings be evaluated. At the same time, generation of too many crew pairings naturally increases the difficulty of the optimization phase. Therefore, in this phase as few crew pairings as possible are generated which allows preservation of the robustness and the quality of the solution.
In this study, crew pairing sets were generated using a dept-first search algorithm (like in reference [7]) in the genetic optimization phase. The dept-first search algorithm is used in phase two of crew pairing generation in a similar manner. First, flight duties are generated from all available flights. Then crew pairings are generated from flight duties with a similar method after duty generation. There is one important difference in the presented approach; in the second crew pairing, the generation phase is repeated for every crewbase for a multibase solution.
4.2. Optimization
In the optimization phase, subsets of crew pairings which satisfy all crew needs and minimize the objective function are searched among generated crew pairings created in the previous phase. This process should be modelledas a set-covering problem and solved with genetic algorithms.
If one considers that F is the set of flights which appears in the flight schedule and P is the set of crew pairings, then the set-covering model for crew pairing problem can be formulated as follows [14].
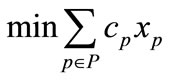 (1a)
(1a)
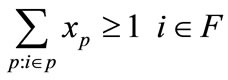 (1b)
(1b)
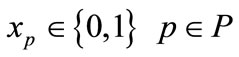 (1c)
(1c)
In the Equation 1(a), 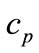 indicates cost value for each crew pairing in P and
indicates cost value for each crew pairing in P and 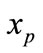 is the decision variable which indicates whether the crew pairing is in the solution set. Hence, Equation 1(a) gives the total cost of the solution. Equation 1(b) is an inequality constraint which guarantees the full covering of all flights in F. If Equation 1(b) gives a value greater than 1 for a flight in F in other words if the solution set has more than one crew pairing which covers a flight, that flight is a dead-head flight. Additional cost will be added for dead-head flights as described in fitness function section. And Equation 1(c) represents standart constraints for the problem.
is the decision variable which indicates whether the crew pairing is in the solution set. Hence, Equation 1(a) gives the total cost of the solution. Equation 1(b) is an inequality constraint which guarantees the full covering of all flights in F. If Equation 1(b) gives a value greater than 1 for a flight in F in other words if the solution set has more than one crew pairing which covers a flight, that flight is a dead-head flight. Additional cost will be added for dead-head flights as described in fitness function section. And Equation 1(c) represents standart constraints for the problem.
Widely used methods for solution of set-covering problem are branch and bound based methods and genetic algorithms. Although branch and bound based methods could converge to more exact values, set-covering problems of a medium sized airline company may have approximately 5000 of rows and 100,000 of columns. Because of the nature of the problem, approximate methods (like in reference [15]) are developped. With this kind of method a much higher convergence rate is obtained for the solution of very large problems like 10000 of rows and 1,000,000 of columns. Genetic algorithms are comparatively powerful candidate in approximate optimization methods.
Unlike other genetic implementations, a new genetic operator—called perturbation operator—is implemented. As can be seen in the experimental results section, by using this operator, the convergence rate has been greatly increased.
4.3. Chromosome Representations for the Set-Covering Problem
Two kind of representations are suggested for using genetic algorithms to solve the set-covering problem. These are column-based representation and row-based representation.
In column-based representation, chromosomes are represented through a binary coded string that is composed of one or zero values. In this representation, each crew pairing is represented by a gene and each gene that could take values of one or zero that indicates whether the particular crew pairing would be in the solution. The only disadvantage of this representation scheme is the infeasible chromosomes that would be formed as a result of genetic operations. Hence, a heuristic feasibility operator has been implemented (in [4]) to cope with this problem.
In row-based representation, the number of genes that chromosomes include is equal to the number of flights. The index of each gene represents the flight and the value of each gene represents the crew pairing which covers the flight. However, in this method it is possible to represent the same solution in different forms because the same crew pairing would be represented by more than one gene. This situation makes the calculation of fitness function ambigious and enables different forms of chromosomes to generate the same solution and fitness value.
Another disadvantage of this method is that the uniform crossover operator, which gives good results in column-based representation, results in too many dead-head flights. This situation might be solved with usage of one or multipoint crossover operators, nevertheless these methods do not give satisfactory results compared to the other method. Likewise, the mutation operator which is applied by changing some genes on the chromosome, increases the number of dead-heads. (See reference [10] in which an implementation of row based representation was studied.)
In this study, column based representation is used and results are improved by using additional genetic operators.
4.4. Generation of First Population
The first phase of the genetic optimization is the population generation process. In order to carry out this process, a random crew pairing assignment should be done for each flight. Unlike study [4], in this study, if there were a flight that had been covered by a crew pairing which had been previously added to the solution, no crew pairing search would be done for this flight. In this way, low numbers of dead-head flights can be obtained. This process can be outlined as follows:
If
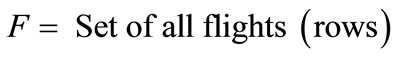

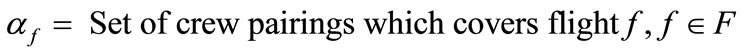
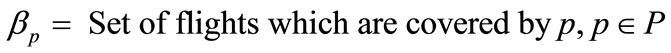
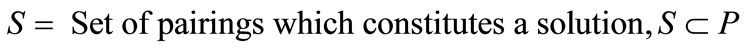
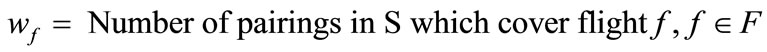
Then 1) 
2) 
a)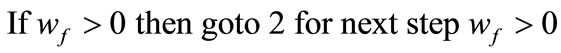 ;
;
b)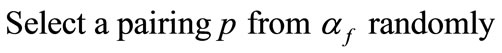 ;
;
c)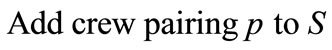 ;
;
d)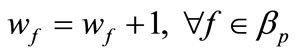 .
.
During the generation of the first population and the next, the iteration phases algorithm always checks to avoid existence of identical chromosomes in the same population. The population size for the crew pairing solution was determined as 20. The augmentation of the number of chromosomes may decrease the number of iterations but it does not provide a decrease in total solution time because it raises the calculation times. After the generation of each chromosome of the initial population using the methods previously mentioned, the genetic algorithm becomes ready to run.
4.5. Genetic Iteration
After the generation of the first population, the main loop of the genetic algorithms is entered and selection, crossover, mutation, and feasibility operators are applied respectively. During these processes, the similar operators which are presented in study [4] are implemented with some modifications.
First, the chromosomes which are used in the crossover operator for reproduction are determined with the selection operator. In the presented work, binary tournament selection is used for the selection operator because it does not need much in terms of extra calculation and runs fast. In this method, two sets which include two chromosomes are composed randomly and one in each two chromosome which has better fitness is chosen for the crossover phase.
Crossover operator can be considered as the transition phase by which the genetic information is passed to new generations, namely child chromosomes are generated in the phase. One or two child chromosomes (depending on the crossover operator implemented) are generated through the crossover operator which is applied to chromosomes of good quality which are taken from the previous population. The fusion crossover operator (which uses fitnesses of chromosomes in a probabilistic way to select genes during crossover operation) is implemented. (The detail of the method can be found in study [4].)
The mutation operator is applied to child chromosomes which are generated in the crossover process to avoid premature convergence; this provides a random search mechanism on a small scale. Usually, it is applied as changing a certain number of genes with a small probablity. In reference [4], it is stated that the use of a variable mutation rate, which is increased with the convergence, gives much better results compared to using a fixed mutation rate. The convergence rate always decreases while the algorithm approach to the optimum solution. Then progress provided by the mutation rate becomes more important than the progress provided by the crossover operator. The number of genes, which will be mutated, nm, is calculated by the Equation (2),
 (2)
(2)
• 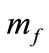 : Maximum value of variable that mutation rate can be.
: Maximum value of variable that mutation rate can be.
• 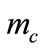 : Iteration step when the variable mutation rate reached to the half of its maximum value.
: Iteration step when the variable mutation rate reached to the half of its maximum value.
• 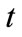 : Iteration step (Number of children which are generated from the beginning).
: Iteration step (Number of children which are generated from the beginning).
• 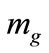 : Gradient of the function at
: Gradient of the function at .
.
In this study, 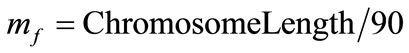 ,
, 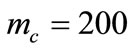 ,
, 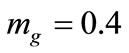 were chosen.
were chosen.
After deciding the number of genes that would be mutated, another parameter which has to be decided is the mutation rate . If a gene were selected to be mutated, the mutation operator would be applied with the probablity
. If a gene were selected to be mutated, the mutation operator would be applied with the probablity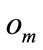 . The value of
. The value of 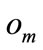 is determined by the ratio of the number of genes which are equal to 1 in the fittest individual of the population and the total length of chromosome (as stated in the study [7]). For instance, if a chromosome had 10 crew pairings in the solution over 100 crew pairings then
is determined by the ratio of the number of genes which are equal to 1 in the fittest individual of the population and the total length of chromosome (as stated in the study [7]). For instance, if a chromosome had 10 crew pairings in the solution over 100 crew pairings then  would be
would be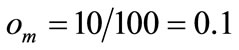 . If
. If  is the chromosome which would be mutated and
is the chromosome which would be mutated and 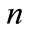 is the length of the chromosome then the mutation operator works like this:
is the length of the chromosome then the mutation operator works like this:
1)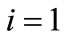 ;
;
2)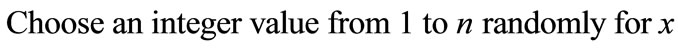 ;
;
3)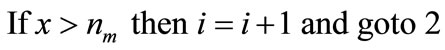 ;
;
4)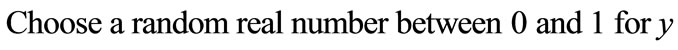 ;
;
5) ;
;
6)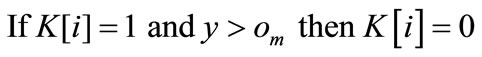 ;
;
7)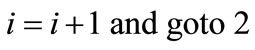 .
.
As stated in previous sections, until now there has been no guarantee about feasibility of chromosomes which are generated or modified by the genetic operators. Therefore a heuristic-based repair operator, called feasibility operator, is used to repair this kind of chromosomes. (For details reader can consult studies [4] and [7]).
4.6. Perturbation Operator Implementation
Unlike other implementations of genetic algorithms, in this study, a perturbation operator is implemented after the feasibility operator in order to enhance the efficiency of the current solution. In this operator, first, the chromosome is made infeasible through the removal of one or more crew pairings which are in the solution. Next alternate lower costs of crew pairings are searched on the chromosome to substitute removed ones to make chromosome feasible like feasiblity operator. This method is called the perturbation operator because chromosomes are made infeasible deliberately. If the search is successful then alternative crew pairings are taken into the solution; if not the chromosome is reverted. The iteration process can be summarized as follows:
If
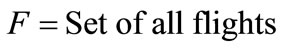
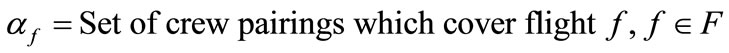
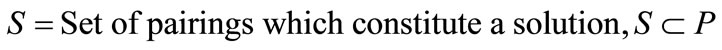
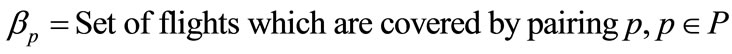
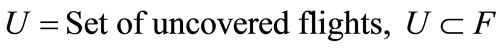
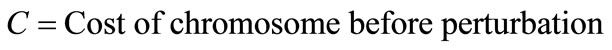
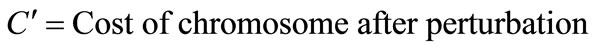

Then 1) 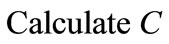
2) 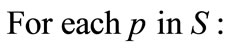
a)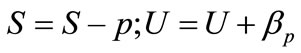 ;
;
b) 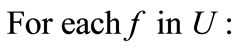
i) Find the first crew pairing  which minimizesratio
which minimizesratio 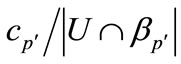
ii) 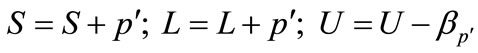
c)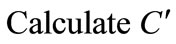 ;
;
d)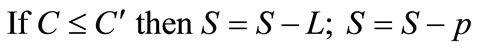 ;
;
e)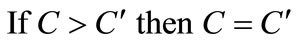 ;
;
f) .
.
This operator is applied with a probability of approximately 0.2 to one randomly selected child after the feasibility operator. The effect of this operation can be seen in the experimental results section. It can also be observed that the genetic algorithm could reach much better solutions in much less iteration and obtain much more robust and stable results in spite of the randomized nature of genetic algorithms.
Furthermore, in step 2, the perturbation operator is applied with dual or trine combinations of crew pairings instead of singular implementation. However, search for the dual or above combinations substantially increases the iteration time compared to singular implementation. Nevertheless, dual or trine implementation of the perturbation operator can be used with a small probablity in the main loop of genetic algorithm or can be applied at the end for the best solution. Even better results can be obtained in this way.
4.7. Fitness Function
Another important issue that has to be determined is the fitness function and the quantities which will be used instead of cost values in this function. Generally, total monetary cost is calculated (like in studies [6] and [1]). First, the cost of each crew pairing in the solution is calculated using the sum of crew salaries for the trip, hotel costs, etc. Then the total cost of of the solution can be calculated by adding these crew pairing costs.
But, as is stated by the crew scheduling department of Turkish Airlines (THY), the minimization of total duration of crew pairings (flight duties + rest periods) was more important than the minimization of total monetary cost. Based on this requirement, in this study the total duration of crew pairings is used instead of monetary cost in fitness function. Regarding this requirement, all terms in fitness function are designed to produce duration-based values.
Another point that must be taken into account is deadhead flights. The proportion of dead-head flights in the fitness function is mutiplied by a coefficient to minimize the numbers of flights because of their attenuator effect on the transportation capacity as stated in previous sections.
Like dead-head flights there is another factor that must be considered and that is the crewbase distribution of crew members. Duty distribution of crewbases has to be proportionate to the number of crew who could be utilized for each crewbase hence crew pairings have to be chosen in order to provide a regular work balance between crewbases. This cost factor is very important for efficient duty assignment for crewbases. The fitness function which is used in this study (Equation (3)) and its paremeters are as follows:
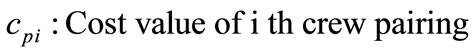 ;
;
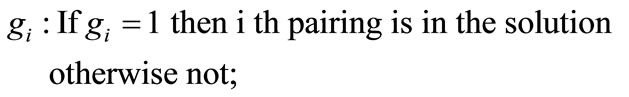
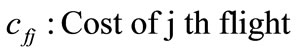 ;
;
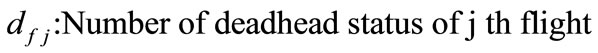 ;
;
 ;
;
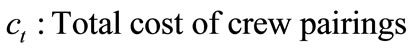 ;
;
 ;
;
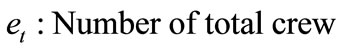 ;
;
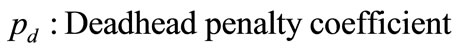 ;
;
then
 (3)
(3)
The cost terms in the fitness function express total duration (duty + rest). The goal of the optimization process is to minimize the total utilization duration of a crew while adjusting workload balance between crewbases. There are three terms in fitness function and all of them give values of same kind.
The first expression in the equation gives the total cost of the crew pairings in the solution—called plain cost.
The second term in the expression is a penalty factor for the flights which are covered by more than one crew pairing (dead-head flights). In this term, the penalty coefficient  has been applied for dead-head flights. (It might be thought that dead head flights are already covered by more than one crew pairing and the cost of the flight itself would already appear in these crew pairings more than one time). But there are additional cost factors inherent in deadhead flights including transport capacity and crew utilization reduction. So there is a requirement of additional cost calculation for other cost factors we could not calculate in the first term. In this presented work for experimental results,
has been applied for dead-head flights. (It might be thought that dead head flights are already covered by more than one crew pairing and the cost of the flight itself would already appear in these crew pairings more than one time). But there are additional cost factors inherent in deadhead flights including transport capacity and crew utilization reduction. So there is a requirement of additional cost calculation for other cost factors we could not calculate in the first term. In this presented work for experimental results, 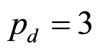 were chosen.
were chosen.
The last term in the expression of fitness function is the crewbase distribution cost which means work balance irregularity. Making proportional duty distribution is very important for efficient crew utilization and for minimizing overtime crew costs. This is done by applying a penalty factor that resides in the ratio difference between total crew pairing duration and the total number of available crews. The number of the total available crew must be proportionate to the total crew pairing duration for a selected crewbase. For example if  = 3500 hours,
= 3500 hours,  hours,
hours, 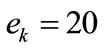 and
and 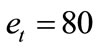 then the penalty coefficient for the crew distribution cost will be
then the penalty coefficient for the crew distribution cost will be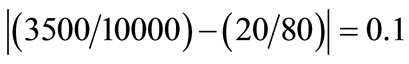 . This means crew distribution cost of the crew pairings which belong to a selected crewbase will be plain cost * 0.1. This increases the plain cost of the solution by 10 percent.
. This means crew distribution cost of the crew pairings which belong to a selected crewbase will be plain cost * 0.1. This increases the plain cost of the solution by 10 percent.
Fitness function integrates three different but dependent objectives. These include minimization of total crew pairing cost, minimization of dead-head flights, and minimization of crewbase distribution cost.
4.8. Population Replacement
The last step of the genetic algorithm is the population replacement phase. In this phase, we decide how to use the chromosomes that are generated and enhanced and how to apply genetic operators. For the solution procedure developed here, the elitist strategy has been used and the order of sequences is as follows:
1) Parents and children are composed in one population;
2) New population is ordered according to fitness;
3) First 20 chromosome are kept for next round.
Furthermore, except for the elitist strategy two more approaches were tested. The first one is the generational approach which is based on all parents were replaced by children and the second one is the steady-state approach which is based on each child chromosome was replaced with a parent which has been selected according to fitness randomly. But elitist strategy gives better results. The test results can be seen in Figure 1. Figure 1 was obtained for the first 200 iterations for just viewing purposes. However, for 10,000 iterations results are similar.
The general schema of genetic iteration is as in Figure 2.
5. Experimental Results
The presented test results were generated under Java NetBeans platform via java codes which were developed for this study. Test hardware was an AMD Athlon 1.8 MHZ single processor machine.
The test data used were taken from the flight schedule of THY (Turkish Airlines) which starts at 25th of March 2007 and ends at 11th of May 2007 (can be found in reference [16]). Flight timetable of Airbus 315 fleet which includes 710 flights was selected as test data. After pairing generation 3308 pairings were generated before optimization phase. It is also assumed that there were two crew bases. One sixth of all crews were considered as located in the first crew base and the rest were considered as located in the second one.
There were four approaches tested. The first is genetic algorithm developed by Beasley and Chu (this approach will be called GA). The second is the genetic algorithm with perturbation operator (called GAPO). The third is the genetic algorithm approach suggested in study [12] (called GA-UnEx). The fourth approach is an exact method based on branch and bound technique with dual simplex algorithm. This last approach gives us exact global optimum for the problem. By using this exact result we are able to evaluate solution qualities of genetic approaches. The exact cost value of the studied dataset was found as 679,005 in 6 mins and 7 secs by using B&B with dual simplex method. While six minutes might look acceptable, the calculation time for the exact methods dramatically increases with the problem size increase.
There are some abbreviations used in the result tables
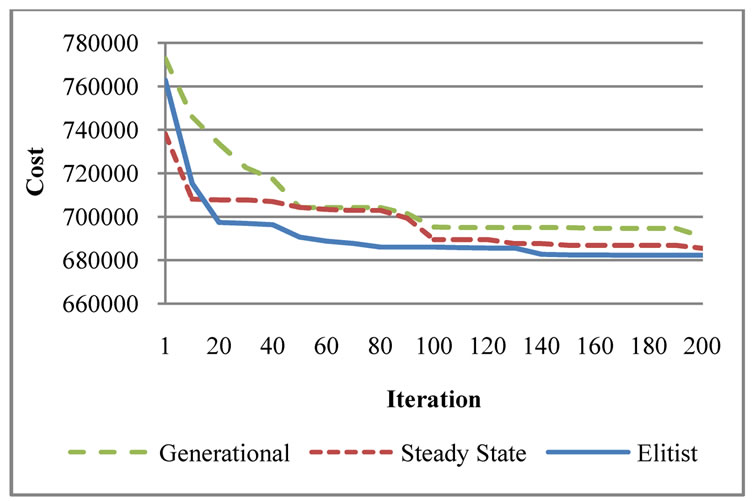
Figure 1. Population replacement strategy.
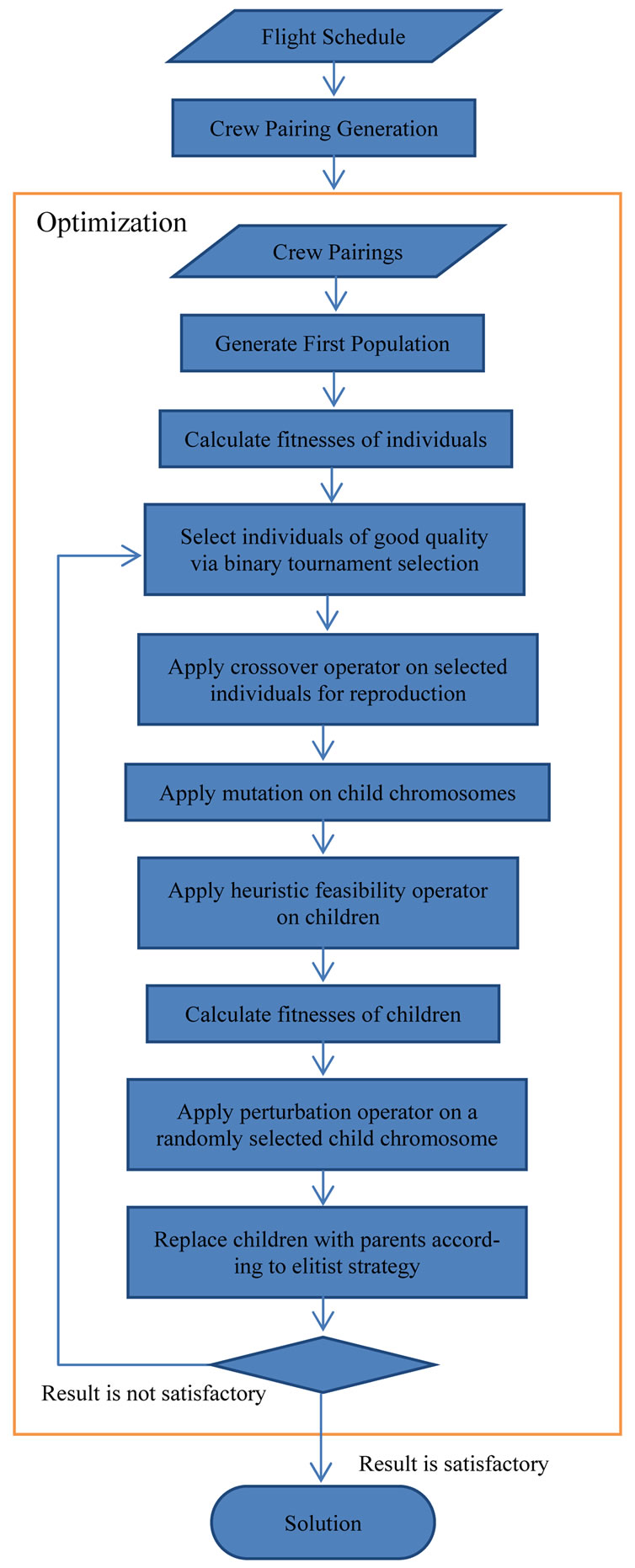
Figure 2. General schema of the system.
to increase readibility. These are given in Table 6.
Table 7 includes values of important optimization parameters at particular iteration steps. Each of three genetic approaches were run for 10,000 iterations. As can be seen in Table 7, GAPO is capable of reaching much

Table 6. Abbreviations.
better results in much less time.
Graphical representations of the results can be seen on Figures 3 and 4. As was mentioned in previous sections because of additional perturbation operators, GAPO needs more calculation time for just one iteration than GA. However, it can converge much faster and total necessary runtime will be much less than GA. GA-UnEx is especially useful for decreasing deadheads, but because of the greedy approach, it is computationally more expensive than either GAPO and GA. Please note that the line represents B&B algorithm shows the final cost value (679,005) we got by using it. It is put for us be able to compare solution quality of other GA implementations.
6. Conclusions and Future Work
In the presented work, airline crew pairing problem is revisited. In terms of crew scheduling problems, crew pairing optimization is the main cost-determining phase. Since crew pairing costs are the second largest operational cost, after fuel costs, well-arranged crew distribution flights might surely increase utilization of the crew and benefit for the airline.
During the development of the presented solution procedure, existing methods were examined, adapted, and improved. Scenarios with multiple crewbases were also simulated using genetic algorithms. From the results obtained one can deduce an incremental increase in convergence rate as well as an incremental increase in robustness applying this new procedure. The perturbation operator implementation has great effect on having this fast and robust convergence. Additionally, the number of dead-head flights is reduced through the application of the strategy developed during the population generation phase. This reduction has a direct effect on the total cost.
Monetary benefit of the results of the new implemented perturbation operator can be calculated with the multiplication by a monetary coefficient because the terms used in fitness function were duration related terms.
This study is also an initial study for the crew rostering phase which is the second phase of the crew scheduling;
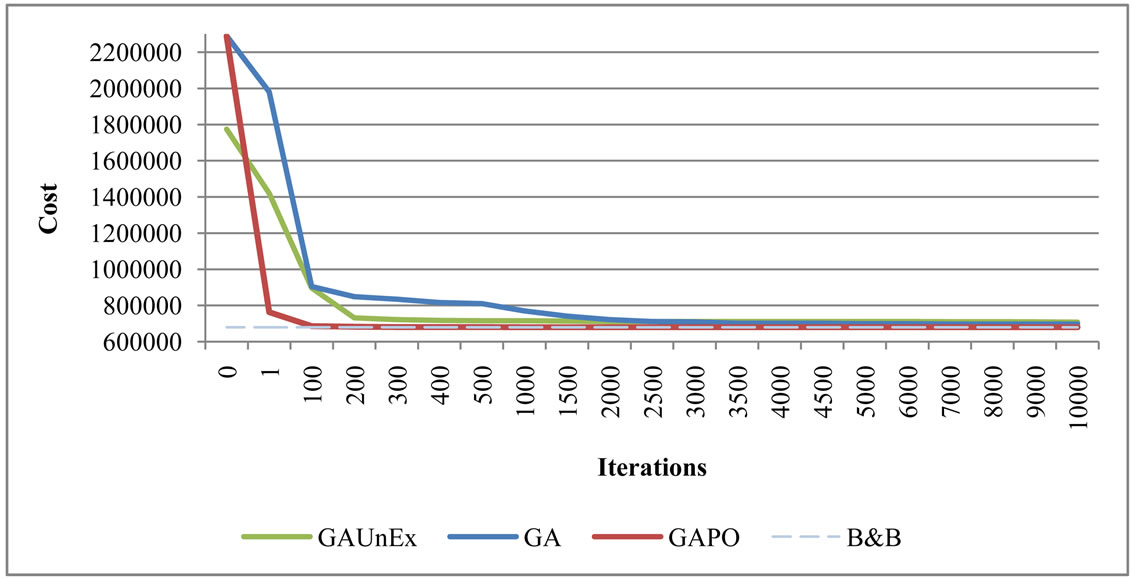
Figure 3. Convergence comparison of applied algorithms.

Table 7. Solution comparison.
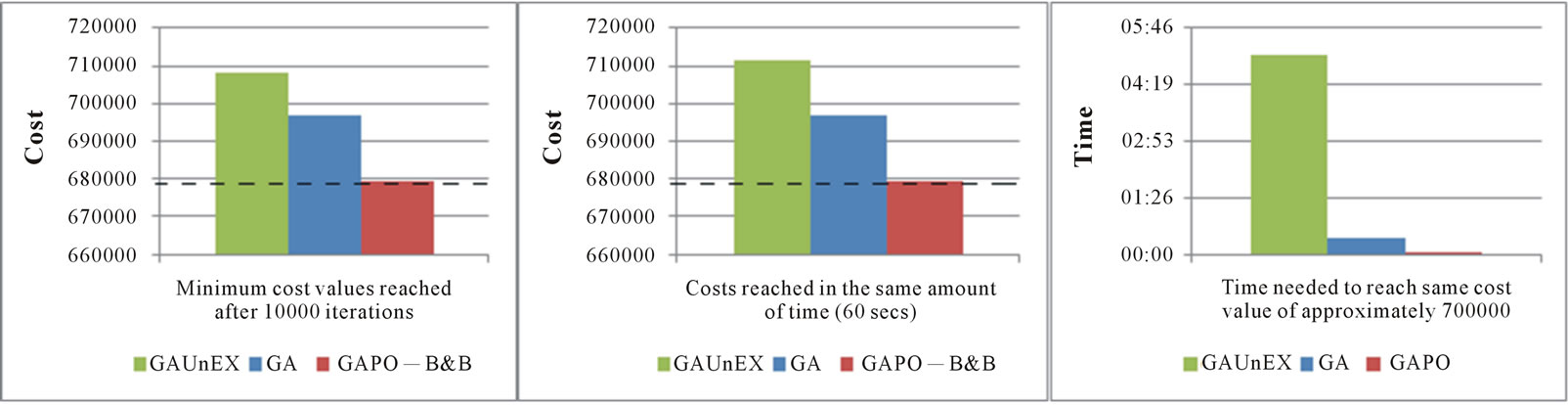
Figure 4. Comparisons in various aspects.
the success of the crew rostering phase is completely dependent on the quality of the results of the crew pairing phase.
The usage of larger populations and perturbation operator with higher probablity ratio can make the algorithm more effective. But in this situation, the run time increases because of the required increase in calculation time. Distributed genetic algorithms can be proposed as a direction for future work to be able to use much larger populations without increasing calculation time.
REFERENCES
- H. T. Ozdemir and C. K. Mohan, “Flight Graph Based Genetic Algorithm for Crew Scheduling in Airlines,” Information Sciences, Vol. 133, No. 3-4, 2001, pp. 165-173. doi:10.1016/S0020-0255(01)00083-4
- F. M. Zeghal and M. Minoux, “Modeling and Solving a Crew Assignment Problem in Air Transportation,” European Journal of Operational Research, Vol. 175, No. 1, 2006, pp. 187-209.doi:10.1016/j.ejor.2004.11.028
- Republic of Turkey Ministry of Transport, Maritime Affairs and Communication, “Instruction on Flying Team’s Task and Resting Terms and Principles of Application,” 2005. http://www.shgm.gov.tr/doc3/sht6a50.doc
- J. E. Beasley and P. C. Chu, “A Genetic Algorithm for the Set Covering Problem,” European Journal of Operational Research, Vol. 94, No. 2, 1996, pp. 392-404. doi:10.1016/0377-2217(95)00159-X
- J. H. Holland, “Adaptation in Natural and Artificial Systems,” MIT Press, Cambridge, 1975.
- C. P. Medard and N. Sawhney, “Airline Crew Scheduling —from Planning to Operations,” 2005. http://www.carmen.se/research_development/research_reports.htm
- H. Kornilakis and P. Stamatopoulos, “Crew Pairing Optimization with Genetic Algorithms,” Lecture Notes in Computer Science, Vol. 2308, 2002, pp. 109-120. doi:10.1007/3-540-46014-4_11
- C. Barnhart, et al., “Branch-and-Price: Column Generation for Solving Huge Integer Programs,” Operations Research, Vol. 46, No. 3, 1998, pp. 316-329. doi:10.1287/opre.46.3.316
- D. Klabjan, E. L. Johnson and G. L. Nemhauser, “Solving Large Airline Crew Scheduling Problems: Random Pairing Generation and Strong Branching,” Computational Optimization and Applications, Vol. 20, No. 1, 2001, pp. 73-91. doi:10.1023/A:1011223523191
- L. F. G. Hernandez, “Evolutionary Divide and Conquer for the Set-Covering Problem,” Lecture Notes in Computer Science, Vol. 1143, 1996, pp. 198-208. doi:10.1007/BFb0032784
- U. Aickelin, “An Indirect Genetic Algorithm for Set Covering Problems,” Journal of the Operational Research Society, Vol. 53, No. 10, 2002, pp. 1118-1126. doi:10.1057/palgrave.jors.2601317
- T. Park and K. R. Ryu, “Crew Pairing Optimization by a Genetic Algorithm with Unexpressed Genes,” Journal of Intelligent Manufacturing, Vol. 17, No. 4, 2006, pp. 375- 383. doi:10.1007/s10845-005-0011-z
- L. H. Lee, C. Ung Lee and Y. P. Tan, “A Multi-Objective Genetic Algorithm for Robust Flight Scheduling Using Simulation,” European Journal of Operational Research, 2007, Vol. 177, No. 3, 2007, pp. 1948-1968. doi:10.1016/j.ejor.2005.12.014
- C. Barnhart, A. M. Cohn, E. L. Johnson, D. Klabjan, G. L. Nemhauser and P. H. Vance, “Handbook of Transportation Science,” Springer, Berlin, 2003.
- D. Wedelin, “The Design of a 0-1 Optimizer and Its Application in the Carmen System,” European Journal of Operational Research, Vol. 87, No. 3, 1995, pp. 722-730. doi:10.1016/0377-2217(95)00243-X
- Turkish Airlines Flight Schedule Document, 2007. http://www.turkishairlines.com/en-INT/online_services/schedule/time_table.aspx

