Journal of Water Resource and Protection
Vol.07 No.09(2015), Article ID:57925,19 pages
10.4236/jwarp.2015.79062
Assessment of Saltwater Intrusion and Discharges to a Wetland with a 3D Transient Variable Density Flow Model: The Coastal Plane Oropesa-Torreblanca Aquifer, Spain
Ignacio Sanz-Garrido, José E. Capilla
Research Institute of Water and Environmental Engineering, Universitat Politécnica de Valencia, Valencia, Spain
Email: jcapilla@upv.es
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 June 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
The proper characterization of coastal aquifers requires modeling variable density flow effects. However, most models estimate processes as saline intrusion based on 2D models with constant density and are rarely calibrated to honor salinity measurements. These facts limit the model predictions reliability, affecting the estimated hydrodynamic parameters, external stresses, and other model outputs that can be critical for planning or management decisions. This paper describes the re-assessment of a coastal aquifer model (Oropesa-Torreblanca, eastern Spain) subjected to moderate-to-high saline intrusion with a transient 3D variable density flow model. Previous models were based on 2D low-resolution grids without variable density effects. The new model honors the observed trends of both piezometric and salinity data. Results show the importance of the variable density effects having on critical outputs as sea intrusion and the discharges to a local wetland of high environmental value. The widespread intrusion process and its current stabilization are confirmed but, compared to previous models, the annual average intrusion is 156% higher, discharge to the wetland increases 30%, and the inflows from neighboring formations increase 22%. The more accurate aquifer models, as well as the new discharges and intrusion estimations, are important contributions for future water and environmental planning decisions in the area.
Keywords:
Salinization, Intrusion, Variable Density, Calibration, Wetland

1. Introduction
Coastal aquifers can be particularly vulnerable to overexploitation, wrong management and pollution, and many coastal planes, in mild climate latitudes, are heavily occupied by urban areas, and agricultural and industrial activities. Besides, these water bodies frequently play a vital role in local supplies. Under these conditions, seawater intrusion, a very common problem all over the world, requires special attention to preserve the quality of water. Moreover, it is quite common to find wetlands of high environmental value strongly dependent on the groundwater body management, both in quantity and quality. This situation is especially relevant in some Mediterranean areas with semi-arid conditions and frequent episodes of water scarcity.
This scenario requires accurate modeling tools to properly characterize the evolution of the water body, establish sustainable water resources planning policies, and monitor groundwater management practices. One of the most common problems found in practical situations is that groundwater modeling tools do not deal with variable density effects and oversimplify the characteristics of the real formation. Thus, when intrusion takes place, this simplified approach leads to improper calibration of models, including hydrodynamic parameters and external stresses over the aquifer. Many authors have dealt with the seawater intrusion modeling problem, being this issue an important open field of research; see for instance [1] - [3] . Besides, it is well-known that variable density induced by salinity changes modifies velocity fields [4] [5] , affecting to the dynamics of the system, the water balance and the location and changes of the saltwater―freshwater interphase.
Under climatological conditions of low rainfall―quite common along Mediterranean seaside areas―seawater intrusion is a permanent threaten to groundwater bodies. This happens in several aquifers located along the East and Southeast coast of the Iberian Peninsula with very intense human activity, where groundwater is essential to supply existing demand, and to maintain the environmental equilibrium of ecosystems associated to wetlands.
The goal of the research described in this paper is to advance in the characterization and intrusion estimation of the Oropesa-Torreblanca coastal aquifer, located in Eastern Spain (see Figure 1), showing the important changes in model results that the improvement in the model yields. This aquifer is important for both the local water supply and the water balance of a natural reserve located in the area known as “Prat de Cabanes”. The geographical coordinates of the center of the study area are 40N11'26'' and 0E10'26''.
There have been remarkable investigation and modeling efforts dealing with this water body, that include a
Figure 1. Location of the Oropesa-Torreblanca coastal aquifer.
long series of piezometric and quality measurements as well as estimation of external stresses―recharge and water abstractions―for a period of 37 years―from 1973 to 2009. The availability is that if this long series of data makes this case study of special interest for research purposes. However, so far all models have been based on simple 2D discretization, not accounting for variable density effects, and model calibrations were only based on piezometric data; see [6] - [8] . This paper presents the development of a far more accurate 3D transient model that includes variable density flow effects, whose calibration is based on both piezometric and salinity; we analyze the changes in model results and then identify issues that required further consideration to improve model predictions.
2. The Oropesa-Torreblanca Aquifer and the Prat De Cabanes Wetland
2.1. Geographical Framework
The coastal plane Oropesa-Torreblanca―name also given to the underlying groundwater body―is located in the Eastern central province of Castellón (Spain), and belongs to the territory of the Jucar River Basin Authority. This coastal plane extends along the seaside for 25 km, reaching between 2.5 and 6 km inland, and covering an area close to 90 km2 (Figure 1) and the underlying groundwater body is referred to as GWB 080.110 by the River Basin Authority as GWB 080.110. Although it is not a large water body, its situation is critical for the local water supply and to maintain the optimal environmental conditions in a wetland area―Prat de Cabanes― located above the aquifer and hydraulically connected to it. The hydrographical network is rarely active. Without permanent or seasonal streamflows in the sub-basins, the runoff is showing most irregular flow―even extreme flows―in humid hydrologic years. The most important sub-basins are Chinchilla creek, with river mouth located North of the city of Oropesa, and Cuevas river―also known as San Miguel river―North of Torrenostra. Other sub-basins of interest are Perchets and Campello creeks, and Mañes and Estopet ravines; these latter sub-basins are active only in the most extreme rainfall seasons.
There is a wetland area of high environmental value known as “Prat de Cabanes”. It is one of the largest in the Region of Valencia (812 ha), and is listed under the RAMSAR convention (Convention on Wetlands of International Importance)―site No. 458 [9] . There is a well-developed typical wetland vegetation with submerged and emergent plants, halophytic and dune communities. There are also a number of endemic plants, fish, and invertebrates, and the area supports several species of nesting birds. Thus, it is also a Special Protection Area (SPA), as recognized under the European Union Directive on the Conservation of Wild Birds [10] . The area extends from Torrenostra to Torre la Sal, with a transversal dimension of 1.5 km. It is permanently flooded, with a relatively slow process of siltation. It was developed through the long-term sedimentation of a coastal lagoon, underlain by extensive areas of peat, and is separated from the sea by a dune complex. The site is nearly pristine. Several authors have described and studied this wetland from different perspectives. Quereda [11] [12] and Segarra [13] provide the first modern analyses centered on the morphology, climatology and hydrology of the area. More recently Castany [14] , in a study about one of the characteristic bird species of the area, provides a comprehensive review of the water budget in the wetland providing other qualitative observations. Other general hydrological or hydrogeological studies, mentioned below, address the underlying groundwater body draining into the wetland, but not the more local hydrological aspects of the wetland. According to Castany [14] , and based on data records from the period 1948-83, the seasonal variation of the rainfall and the groundwater table usually result in a very important reduction of the water surface of the wetland during late spring and early summer. This author also describes, without quantification, the process of seasonal salinization of the wetland water due to low rainfall, saltwater intrusion and tides. Besides, Castany also provides an estimated water balance in which the wetland receives water from the aquifer (4.3 hm3/yr), runoff from agriculture watering (12.7 hm3/yr) and direct rainfall (7 hm3/yr). At the same time, there is an estimated flow of 3.9 hm3/yr through three different channels to the sea (known as Gola del Trenc from the Northern part of the wetland, SèquiaVella from the central part and Gola de Torre la Sal from the Southern part). These figures provide a water inflow of 20.1 hm3/yr that would result in an excess of water not pointed out in the wetland studies. In fact, according to the conclusions from different studies developed for the Spanish National Hydrologic Plan [15] , the hydrologic equilibrium of the area is seriously threatened and it is posing a severe risk for the wetland in terms of water balance and water quality. We guess that the two balance terms worse estimated in [14] are runoff from agriculture watering and discharges to the sea through channels.
2.2. Hydrogeological Framework
The hydrogeological formation is made up by detrital materials of Plio-quaternary age. The formation limits with other neighboring aquifers and receives underground flows from them. The aquifer thickness grows from the inland western areas towards the coastline, reaching a maximum of 125 m near the San Miguel river mouth and of 85 m near Chinchilla river mouth.
The formation overlays an impervious layer made up by marls and clays of Miocene age, which also include some intercalated limestone and conglomerate zones. However, this lower limit does not extend below the whole aquifer [6] [8] as it will be shown below when defining the mathematical model. The Plio-quaternary materials of the formation limit, as shown in Table 1, mainly with Cretaceous and Jurassic that are part of the Maestrazgo aquifer. This happens also vertically, according to the interpretation of previous studies [8] . Thus, the northern, southern and central parts―this one to a less extend―of the Plio-quaternary formation are connected vertically with the underlying Maestrazgo formation. The hydraulic connection between the two formations takes place through three different subaquifer levels differentiated in the Maestrazgo aquifer: the northern part corresponds to the Jurassic materials, the central part to Aptian and Cenomanianlimestones―Cretaceous period―, and the southern part through Aptian Cretaceous materials.
The groundwater flow shows a general direction NW-SE that is locally changed due to the intense exploitation of the aquifer. These intense abstractions also induce marine intrusion. According to the first specific studies of the formation, the estimated transmissivity values range between 100 and 2.500 m2/d and the specific yield between 2% and 12% [6] .
2.3. Previous Mathematical Models
As indicated above, the first specific hydrogeological study has been carried out by Morell [6] . This author also presents a hydro chemical study, compiling all existing data in order to determine the causes and consequences of saline intrusion. Some years later other remarkable efforts, IGME [7] , have been done to calibrate a 2D steady state flow model, and more recently Renau-Pruñonosa et al. [8] [16] , with the goal of better determining intrusion phenomena, understand the existing seawater intrusion evolution and propose actions to remediate it. These studies have been focused on the determination of an ecological volume of abstraction to prevent the increment of seawater intrusion. However, all these models have the limitation that have not been calibrated to reproduce salinity data and do not account for variable density flow effects. It is well known that accounting for variable density effects modifies the flow field [4] affecting the dynamics of the system and the evolution of the saltwater-freshwater interphase. Even a 2D model [4] [5] can account for variable density effects although would not be enough to model the seawater interphase effects; this requires a 3D model. Besides, reproducing as much measured data as possible improves the reliability of the model. Thus, it is clear that an accurate understanding of the dynamics between the wetland and the aquifer together with the sea intrusion problem requires a more accurate that includes variable density, calibration including quality data and a 3D model.
Table 2 shows a comparison of water balance in the whole aquifer for both previous models. The main differences between the two models are that the second one is transient and uses more precise data for both recharge (surface infiltration) and abstraction. Thus, the second model [8] is expected to yield more reliable results. Also, there is a slight difference in the total surface extension of the aquifer due to changes in the hydrogeological knowledge of the formation and the administrative criteria to delineated the exact limits of the groundwater body. In this study we use the Jucar River Basin Authority definitions [17] . This fact changes surface infiltration
Table 1. Neighboring aquifer levels, lithology and geological age according to [6] [8] .
Table 2. Water balance comparison between previous models: figures taken fromIGME [7] and Renau-Pruñonosa [8] .
and wells abstraction (see Table 2) but still allows comparing the other terms of the water balance. The results of these models show an important difference for sea intrusion and drainage to the wetland. The newer model [8] gives an intrusion result 70% lower than [7] , while the discharge to the wetland is also reduced more than 60 %; if compared to the estimation given by Castany [14] the reduction is 70%. Although the newer model is more precise, it still lacks some basic features required for a coastal aquifer model, and it has not been calibrated to reproduce salinity data. The two basic critical issues to characterize the status of this groundwater body are precisely saline intrusion and the sustainability of the wetland flows. Then, a more complete model that includes variable density flow effects and vertical flows, calibrated to reproduce also existing salinity observations, would provide a much more robust framework to understand the dynamics of the water body and assess its current and future status.
3. Mathematical Model
3.1. General Considerations and Conceptual Model
After a careful revision of previous hydrogeological studies, and not having additional field data, the basic assumptions regarding the hydrogeological formation are maintained for the new model. The elements that make up the conceptual model are maintained like in the previous models [7] [8] : the formation (Plio-quaternary materials) receives inflows from the neighboring Maestrazgo aquifer, rainfall infiltration and agriculture irrigation runoffs (urban areas do not provide additional recharge to the aquifer); the water balance is completed with water abstractions, discharges to the sea and wetland and intrusion. Pumping data for the whole simulation period has been estimated, on a monthly basis, using different sources of information that include water administration reports, records from water users unions and other technical reports. In the new model we use the transient recharge and pumping data considered in the previous model [8] which are defined on a monthly basis and based on different studies also cited in the cited work. The time framework for the calibration and simulations is the period 1973-2009. It is a very long period of data compared with the usual length of data in most hydrogeology studies. To avoid unnecessary repetition of graphs, the annual values of water abstraction and surface infiltration are shown below in the Figures included for the water balance of the aquifer. Total abstraction has an annual average of 32.93 hm3/yr, starting with 23.14 hm3/yr in 1973, increasing up to a maximum of 45.65 hm3/yr between 1985 and 1990, and then decreasing slowly to a minimum of 18.86 hm3/yr in 2008 and 2009. The average annual pumping rate is 32.93 hm3/yr. The location of wells is quite distributed along the aquifer and it is shown in Figure 2. The annual surface recharge amounts are highly dependent on the estimated annual estimation of infiltrated rainfall. Thus, the total annual surface recharge ranges from a minimum of 5.56 hm3/yr to a maximum of 18.02 hm3/yr, with an average of 9.23 hm3/yr.
The first important improvement in the new model presented in this paper is the discretization (more detail information is given in [18] ). The previous model includes one layer representing the Plio-quaternary aquifer, and an underlying layer representing Cretaceous and Miocene materials. The latter is introduced in the model to reproduce lateral and vertical flows from the Maestrazgo aquifer system, and the impervious bottom layer corresponding to the Miocene materials. The horizontal discretization of this previous model is of 500 × 500 m and includes 1440 active discretization blocks. The new discretization has a higher resolution, 250 × 250 m, includes also the underlying Cretaceous-Miocene formation as a discretization layer, and the Plio-quaternary aquifer is discretized into six layers. In short, we keep the lowest layer to represent Cretaceous and Miocene materials from which the Oropesa-Torreblanca is recharged, and adopt a vertical discretization of six layers. Thus, the
Figure 2. Discretization of every layer from upper (1) to lowest (7), with indication of the locations of pumping wells, cells with drainage to the wetland and boundary conditions (B.C.).
model has seven layers as shown on Figure 2. The deepest zones of the overlying Plio-quaternary aquifer have a thickness of 125 m and the layers have been geometrically defined to be continuous and parallel to the underlying Cretaceous-Miocene formation. There are a total of 3942 active cells distributed in the six layers, and a total of 5035 including the lowest layer. Additionally, 331 cells distributed along the SE border of every layer represent the condition of constant head for the border connected to the sea as shown in Figure 2. The upper layers have less active cells and the sixth layer―lowest layer of the Plio-quaternary formation―has the highest number of active cells.
The lowest layer―seventh layer―extends only to the Cretaceous and Jurassic materials and the cells corresponding to impervious Miocene bottom are deactivated. In this layer the cells with General Head Boundary (GHB, a flow package available in MODFLOW [19] ) correspond to those that control the lateral inflows from Maestrazgo aquifer into the model. Thus, this inflow depends on a prescribed external piezometric level and on a conductance parameter at every cell. It is known that the piezometric levels along the NW border in the Maestrazgo aquifer are quite stable, experimenting very low fluctuations.
The discretization cells with drainage to the wetland are also identified in Figure 2. Thus, the discharge to the wetland Prat de Cabanes is simulated using the drain flow package available in MODFLOW. The drainage condition is located in 126 discretization blocks distributed in three layer (39 in layer 3, 66 in layer 4 and 21 in layer 5); note that the previous model [8] simulates the drainage condition in just 13 blocks in the layer representing the Plio-quaternary aquifer. The boundary condition along the coast is represented by prescribed head boundary condition as shown in the same Figure.
The piezometric and salinity measurements used below for the calibration for the period 1973-2009 have been obtained from the database maintained by the Jucar River Basin Authority [17] . Figure 3 shows the location of data measurements―salinity and piezometric head observations―identified with the codes used by the Basin Authority.
Figure 3. Location of piezometric and salinity measurement points.
The modeling tools used to build the mathematical model are MODFLOW [19] and SEAWAT [20] . The first is a well-known modular finite differences computer code that solves the differential equation that governs flow in saturated porous media. However, in order to account for variable density effects we have used the model SEAWAT [20] . Both models have been used by means of the current version (v 8.0) of the graphic user interphase PMWIN [21] . SEAWAT is a model based on MODFLOW and on the multi-species transport model MT3DMS [22] . It allows 3D variable density flow simulations and has been used and validated in an extensive variety of hydrogeological studies involving coastal aquifers or brine flows. It is a public domain and open source model; this fact facilitates the transmission of the model to other potential users. In this study, SEAWAT is used with variable density flow effects. The model couples the flow and mass transport equations using an internal iteration process in which the flow and transport equations are solved with a progressive updating of the densities and of the flow velocity field.
Under variable density conditions, and expressed in terms of equivalent freshwater head, hf, the flow equation adopts the form shown in Equation (1), see [20] ,
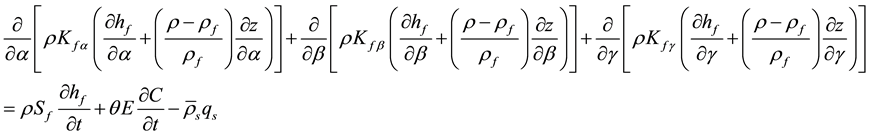 (1)
(1)
where, α, β and γ are the coordinates of an orthogonal reference system aligned with the principal direction of the hydraulic conductivity tensor; refers to elevation with respect to a reference;
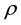 density and
density and
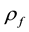 freshwater density;
freshwater density;
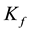 refers to the equivalent freshwater hydraulic conductivity;
refers to the equivalent freshwater hydraulic conductivity;
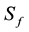 refers to the equivalent freshwater specific yield; t refers to time;
refers to the equivalent freshwater specific yield; t refers to time;
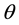 is the effective porosity; C solute concentration;
is the effective porosity; C solute concentration;
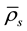 fluid density
fluid density
for external stresses;
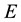 refers to
refers to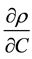 , and refers to external stresses, for both flow sinks and sources.
, and refers to external stresses, for both flow sinks and sources.
Note that the coupling of the flow and transport equations is done assuming that changes in density are only due to concentration, neglecting the effect of pressure and temperature. This is based on the equation proposed by Baxter & Wallace [23] , as shown in Equation (2),
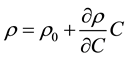 (2)
(2)
where,
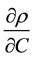 is approximated as 0.7143, generally accepted for conditions similar to seawater. An alternative and simpler approach, not followed here, would consist in neglecting the term
is approximated as 0.7143, generally accepted for conditions similar to seawater. An alternative and simpler approach, not followed here, would consist in neglecting the term


The initial piezometric heads and salinity fields were obtained interpolating the data available from the Jucar Basin Authority [17] . However, the location and amount of data was not enough to have an accurate estimation and the initial interpolated estimation was re-adjusted through the calibration process [18] . External prescribed heads for the GHB condition at the lowest layer were taken from [18] that establish a different external zones for different precipitation intensities and observed piezometric heads.
3.2. Calibration of the Flow Model
The calibration of the model has been based on a trial-and-error procedure following a simple strategy described below. We considered that the complexity of the model and the uncertainties of the formation hydrodynamic parameters were too high to initiate the application of automated, stochastic or not, inverse modeling methodologies in search of a high resolution model with a realistic reproduction of the formation heterogeneity. Besides, the quantification of the recharge from the Maestrazgo formation is still a discussed component of the model water balance, and it has a great influence on it. Moreover, available data are strongly affected by dynamic effects, due to the proximity to pumping wells, at temporal and spatial scales much lower than the size of the model cell and of the monthly time scale at which external stresses are estimated. Thus, we adopted a general strategy of starting with simpler approaches improving the calibration step by step, and even iteratively, towards a more plausible model describing the basic trends of historic measurement records. This strategy is also implicit in the model developed in this paper and the goals of future research in the formation: our model is intended to be the starting point where to apply more sophisticated approaches in search of realistically reproducing local heterogeneity. Low range heterogeneity can have both local and global influence on flow and transport in the formation.
Following these general considerations, the calibration is organized in two steps. The first (described in this section) consists in the calibration of a flow model, with no density effects, to honor piezometric data. Later, as shown in the next section, the calibrated flow model parameters are used as an initial guess to calibrate the coupled flow and mass transport model including the matching of salinity data. This process also allows assessing the impact in results due to improving the modeling approach. After the calibration is completed, a sensitivity analysis is performed to help establishing a general assessment of the validity of the model. The calibration of the flow model has followed these steps:
1) Initial setup of the model using parameters (hydraulic conductivity values and zoning, specific storage, specific yield, conductance values, external heads, etc.) from the previous model [8] . The initial piezometric head field is obtained interpolating available observations.
2) Trial-and-error adjustment of initial piezometric head field to honor the trends of head observations.
3) Trial-and-error iterative process―following the sequence hydraulic conductivity, specific storage, specific yield, conductance of GHB and conductance of drains (wetland)-to improve the matching of piezometric head trends.
4) Final adjustment of K to improve, locally, some piezometric observations that were poorly honored. This has led to modify the previous zoning of K.
A more detail description of the calibration process is given in [18] . All the flow simulations were done solving the equations by the preconditioned conjugate gradient package 2 implemented in MODFLOW and using a maximum head change criteria of 0.001 m. The stress periods (month) were discretized in 10 time steps using a multiplier of 1.08 to increase the accurateness of results at the beginning of every month. Figure 4 shows the final calibrated conductivities for the Plio-quaternary aquifer and the Cretaceous formation.
Figure 4. Hydraulic conductivities calibrated for the flow model without variable density effects for the Plio-qu- aternary aquifer, on the left, and for the underlying Cretaceous-Miocene layer, on the right ocation of piezometric and salinity measurement points.
Although the zoning of the aquifer domain is simple, it has been increased from 5 to 7 zones with respect to the previous model [8] . There are two areas of higher K (200 m/d), the first following the San Miguel river in the Northern part, and the second one closed to the wetland―these two zones are closely as in the previous model [8] . Other two zones with quite high K (125 m/d) correspond to the area of discharge of coastal springs near the city of Alcoceber, and to the Desierto de las Palmas area in the eastern part. The wetland Prat de Cabanes also covers areas with 50 m/d to the North and of very low K (1 m/d) towards the sea. The underlying Cretaceous formation has been considered as a unique zone and has an estimated K of 10 m/d. Vertical hydraulic conductivities have been estimated as one order of magnitude lower than horizontal conductivities (thus ranging between 0.1 and 20 m/d), as in [8] . Figure 5 shows the values of hydraulic conductance calibrated for the GHB conditions in the Cretaceous layer, and for the drain condition used to simulate the discharge to the wetland Prat de Cabanes. Table 3 shows the values calibrated for the specific storage (SS) and specific yield (Sy), which have been differentiated for the upper and lower materials, being much lower for the underlying Cretaceous materials.
3.3. Calibration of the Flow and Transport Model with Variable Density Flow Effects
A major objective of the research described in this paper is to improve the model taking into account variable density flow effects and calibrating taking into account piezometric and salinity data. As mentioned above, the mathematical computer code used is SEAWAT. It is used coupling the flow and transport equations as solved by MODFLOW and MT3DMS, and adopting a hybrid method of characteristics to simulated the advective component of transport. The inflow from the inland boundary does not provide any salts mass to the groundwater body. The boundary conditions of the mass transport model MT3DMS include constant concentration at cells representing the sea (cells shown as prescribed head B.C. in Figure 2), and has zero concentration flow condition everywhere else. The horizontal transverse dispersivity was set as 10% of longitudinal dispersivity at every model cell; the same estimation was used for the vertical transverse dispersivity. The distribution of longitudinal dispersivity for the whole model was initially set as 125 m. This was a low value (compared to the cell size of 250 m) later reconsidered during the calibration. The initial salinity maps were inferred from observations and recalibrated to fit the initial trends of salinity evolution where information is available.
In short, the trial-and-error calibration of the coupled flow and transport model followed the steps below. Note that the specific storage and specific yield are not mentioned in the process description. This is because after
Figure 5. Hydraulic conductivities calibrated for the flow model without variable density effects for the Plio-quaternary aquifer, on the left, and for the underlying Cretaceous-Miocene layer, on the right location of piezometric and salinity measurement points.
Table 3. Effective porosity, specific storage and specific yield estimated by Renau-Pruñonosa [8] and in the new model (without variable density flow effects).
some initial model simulations we found a very low sensitivity of the model to these parameters to honor salinity data.
1) Initial setup of the model using flow model parameters (hydraulic conductivity values and zoning, specific storage, specific yield, conductance values, external heads, etc.) obtained in Section 3.2, and mass transport model parameters as indicated above.
2) Trial-and-error adjustment of initial salinity field to honor the trends of salinity observations.
3) Trial-and-error iterative process―following the sequence hydraulic conductivity, conductance of GHB and conductance of drains (wetland)―to improve the matching of piezometric head trends and salinity data.
4) Trial-and-error iterative process to modify the initial dispersivity of 125 m to improve the matching of salinity observations trends.
5) Repetition of step 2 to locally adjust K and conductance of drains.
The calibration of the coupled model including both piezometric and salinity data led to modify some of the previous estimated parameters. We just modified hydraulic conductivity field and hydraulic conductance of the drain condition at the wetland. The hydraulic conductance of the GHB condition in the Cretaceous-Miocene layer was not changed remaining as calibrated for the flow model in 3.2.
The hydraulic conductance in the wetland area has changed considerably; the area where conductance was of 1000 m2/d―see Figure 1―is now changed to 400 m2/d, and the area of 2000 m2/d to 1000 m2/d. Note that the most recent estimations of hydraulic conductance previous to this paper [8] were between 20,000 and 40,000 m2/d. On the other side, the changes of K, with respect to the initial calibration in Section 3.2, are represented in Figure 6. These modifications are due to the double objective of matching piezometric and salinity data trends
Figure 6. Changes in hydraulic conductivity from the flow model to the coupled flow and transport model with variable density flow effects.
while accounting for the effects of variable density flow. As a consequence, K is changed in two ways: first it is generally reduced from 10 m/d to 1.5 m/d in the Northern part of the Cretaceous-Miocene underlying formation ―layer 7―, and second, it is reduced along the coastline, and more in the deepest layers. This latter change is due to the fact that the model does not represent the real physical flow/transport distance from the grid blocks that are next to the prescribed head cells to the seawater body. This is corrected, in the calibration process, reducing K at the aquifer border―grid blocks next to prescribed head cells―for deeper layers. Besides, we also take into account the real physics of the system by adjusting the prescribed salinity conditions at constant head cells; thus, the salinity increases from the upper layer to the lower one. With these changes there is a better adjustment of salinity data and the cross sectional profile of salinities barely reproduces the expected profile observed in seawater intrusion phenomena. The dispersivity parameter was also calibrated to increase dispersive flow in deeper zones of the formation. We increased its values to 230 m in the deeper areas of the model, keeping the initial value in the upper parts as 125 m. This issue would require more research; we justify greater values at deep zones to account for macrodispersivity effects due to the heterogeneity not represented in the model. Note that hydraulic conductivity has been reduced in lower cells next to the constant head boundary, and that this decreases advective flow.
3.4. Sensitivity of the Coupled Flow and Transport Model to Selected Key Parameters
In order to test the robustness of the results of a model to the uncertainty of parameter and external stresses as well as for increasing the understanding of the relationships between input and output variables, we performed a simple sensitivity analysis with a one-at-a-time approach, i.e., moving one input variable, while keeping the others at their calibrated values, and repeating this process for selected key parameters of the model. This approach does not fully explore the input space, since it does not take into account the simultaneous variation of input variables but provides a simple way to gain confidence and understanding of the model.
The parameters selected for the analysis were hydraulic conductivity (K), aquifer recharge (R) from surface infiltration, and hydraulic conductance of the GHB―that governs the lateral recharge (LR) in the lower layer from the Maestrazgo formation. Thus, six alternative simulations were run: hydraulic conductance governing the GHB condition in the underlying Cretaceous incremented and decreased 25% (simulations LR + 25% and LR − 25%), K incremented and decreased 25% over the whole model―including vertical K (K + 25% and K − 25%), and recharge over the whole Plio-quaternary aquifer incremented and decreased 25% (R + 25% and R − 25%).
The results of these simulations deviate smoothly from the calibrated model, without abrupt changes, demonstrating the plausibility and robustness of the calibration. Figures 7-9 show the alternative simulations together with observed data and simulated heads at control point 08.11.014 (location shown in Figure 3). At this point it can be observed that the greatest impact happens when the lateral recharge―conductance―is changed. In general, results in these Figures show that the model is more sensitive to changes in lateral recharge than to surface recharge. This is not surprising because the inflows from the Cretaceous layer are very important and constitute the main and most important compound of the water balance.
Figure 7. Sensitivity of simulated piezometric head, at control point 08.11.014, to changes of hydraulic conductance at GHB condition―lateral recharge.
Figure 8. Sensitivity of simulated piezometric head, at control point 08.11.014, to hydraulic conductance changes over the whole model.
Figure 9. Sensitivity of simulated piezometric head, at control point 08.11.014, to changes in recharge.
Figure 10 shows the sensitivity analysis of salinity at 08.07.012, a point located not far from the previous one (08.11.014) and close to the wetland. The model reproduces the horizontal trend of salinity, without honoring the small time scale oscillations. Besides, the sensitivity to the different parameter changes is quite low.
Figure 11 shows results at another control point located at the Northern border of the wetland. In this case there is a long-term slightly trend change, more remarkable in the case of higher lateral recharge. Anyway, the impact in model results is very low in every sensitivity simulation.
In general, the behavior of model results in the different simulations is more or less as it has been shown in Figures 5-9. The calibrated model is robust enough in the sense that small changes in the key basic parameters do not lead to important changes in model results. However, it must be pointed out that sensitivity to lateral recharge is high and that the increment of this inflow component can improve the matching of salinity data. However this change worsens the reproduction of piezometric data due to the elevation of the piezometric surface. A more accurate calibration that improves simultaneously the matching of head and concentration data would require a higher degree of reproduction of heterogeneity of K and possibly less smooth variation of external stresses with time. Note that, although the calibration period is very long―37 years―some data are not the result of direct measurements as correspond to estimations [7] [8] .
Table 4 shows the impact of the above sensitivity scenarios on the overall aquifer annual water balance. Apart from the strong impact of the lateral recharge on the aquifer balance, there is a remarkable effect of the reduction of K on the sea discharge. Further efforts to improve the model should address the possibility of improving the estimations of the lateral recharge―Cretaceous underlying inflow―and also on the distribution of hydraulic conductivity over the aquifer. The relatively low sensitivity of intrusion and discharges to the wetland with respect to K makes the model a robust tool to analyze these two basic model results.
4. Results and Discussion
The graphs shown in Figure 12 show simulated piezometric heads against observed data at different locations from North to South of the formation, including areas close to the coast and the wetland. The general trend of the 37 years of historical records is quite well matched. However, the reproduction of the small-scale variations is honored poorly. This is a result we should expect for this model due to a variety of reasons. Firstly, the space and time scales of the model cannot capture the small-scale oscillations that measured data usually display; most piezometric observations are close to pumping areas, or even at pumping locations, leading to dynamic piezometric levels whose reproduction is not plausible with a field scale model. Besides, a high-resolution model
Figure 10. Sensitivity analysis of simulated salinity at control point 08.07.012.
Figure 11. Sensitivity analysis of simulated salinity at control point 08.11.016.
Table 4. Sensitivity analysis of the aquifer water balance (percentage change in brackets).

Figure 12. Simulated and observed piezometric heads (m.a.s.l.) at control points: (a) 08.11.029; (b) 08.11.014; (c) 08.11.023, (d) 08.11.025; (e) 08.11.006 and (f) 08.11.018. Simulated values are represented with a continuous line; time scale in days.
would not be feasible due to the lack of high-resolution data. Secondly, external stresses are obtained combining different approaches as explained in [8] [18] . Thus, for instance, pumping data are partially inferred from the water needs for crops irrigation at every time period, being the total abstractions quite homogeneous in time, as shown in Figure 14 (water balance over the aquifer); rainfall infiltration is also an estimated inflow that does not take into account that the effective infiltration can change importantly depending on the frequency and intensity of the rainfall events. Another important simplification of the model, that seems to work reasonably well, is the simulation of the inflows from the Maestrazgo aquifer (based on the GHB condition in the lower layer). These facts, together with the simple zonation adopted for the hydraulic conductivity, can explain the low scale deviations in the presented graphs.
The central part of the formation is the area in which the calibrated model better reproduces data. The control point 08.11.029, graph (a) in Figure 12, located in the Southern part of the aquifer, presents a worse adjustment possibly due to the situation close to the border of the formation and to string dynamic levels, although the data trend is barely reproduced.
Figure 13 shows the reproduction of salinity data at four different locations along the formation. The calibrated model is able to reproduce the general trends, roughly honoring the base line situation of salinity over time. However, there are temporal peaks not reproduced by the model. We guess that this is possibly due to local phenomena associated with dynamic levels and also with up-coning effects but there is not enough information to fully support this conjecture. Besides, the simple zonation of the model, which is far from reproducing the natural patterns of heterogeneity of K, introduces another important limitation for the simulation of salts transport.
Figure 14 and Figure 15 show the evolution of the annual water budget of the model. These results present some of the most important outputs pursued by thisresearch: the estimation of saltwater intrusion and the discharges to the wetland Prat de Cabanes. In order to assess the influence of a variable density approach on the results, Figure 14 presents results of the flow model calibrated without variable density flow effects (as explained in section 3.2 of this paper), and Figure 15 the final results for the coupled mass and transport model with variable density effects. Note that the most accurate model results―for the coupled flow and transport model―, represented in Figure 15, show the following general features: less recharge from the Cretaceous formation (lateral recharge in lower layer), less discharge to the sea, slightly increment of saltwater intrusion, and more discharges to the wetland (drain). Besides, the time series of annual water balances shows three peaks of

Figure 13. Simulated and observed salinity concentrations (g/l) at control points: (a) 08.11.012; (b) 08.11.039; (c) 08.11.016 and (d) 08.11.006. Simulated values are represented with a continuous line; time scale in days.
Figure 14. Simulated annual water balance without accounting for variable density flow effects.
Figure 15. Simulated annual water balance when accounting for variable density flow effects.
saltwater intrusion for the periods 1980-81, 1984-88 and 1993-94, in both Figures. Moreover, when variable density flow effects are accounted for, the intrusion peaks at 1985-86 and 1994 surpass the water discharges to the sea. These situations correspond to the intense underground exploitation between 1984 and 1994, combined with reductions of rainfall at specific time periods 1977-78, 1982-83 and 1991-92. Table 5 summarizes these results including a comparison with the most recent and accurate previous model [8] .
Due to the small changes in the model extension the infiltration and wells abstraction values given in Table 5 differ between [8] and our model. The previous model extension, IGME [7] , was also different from [8] due to hydrogeological and administrative considerations. Anyway, saltwater intrusion estimations have varied considerably. They go from the first estimations of 2.20 hm3/yr in [7] , see Table 2, to 0.65 hm3/yr in [8] . The new model increases by 150% the latter estimation, 1.67 hm3/yr, and also shows that the intrusion estimation is closer to the previous one in [8] when not modeling variable density flow effects. This fact highlights the impact of neglecting the influence of variable density flow and transport in the overall water budget of the formation. Other important result is the discharge to the wetland Prat de Cabanes. The initial estimation of IGME [7] was of 3.5 hm3/yr, notably higher than the most accurate result given by Renau-Pruñonosa [8] , 1.28 hm3/yr. The new model, with non variable density and calibration of piezometric data, yields a very close result of 1.23 hm3/yr. Again, when variable density effects are accounted for, and the calibration includes salinity data, the new estimation
Table 5. Average water balance comparison for the previous model [14] , and the calibrated model with and without accounting for variable density flow effects.
deviates from the previous yielding 1.68 hm3/yr―31% increment. Another difference in the average water budget affects discharge to the sea and the recharge from the Cretaceous formation through the GHB condition. The former is now 9.24 hm3/yr, also close to the previous estimation of 9.04 hm3/yr. Although the latter shows an increment of 22%, it is not very meaningful because the extension of the model has increased, and the new model has a larger area through which the recharge from the Cretaceous formation enters the Plio-quarternary aquifer.
5. Conclusions
The coastal plane Oropesa-Torreblanca aquifer is a formation that has been studied for decades and provides, as a case study or field lab, a remarkably important data set for further studies. The length of the time period for which there are estimations of infiltration and abstractions, as well as measurements of piezometric data and salinity concentrations is remarkably long: 37 years.
The new mathematical model presented in this paper has important improvements compared to previous models. It is a 3D model with six layers representing the Plio-quaternary formation and including variable density flow effects. It also has a higher resolution grid and a more dense zoning of hydraulic conductivity (K) for calibration purposes. The model has been calibrated reproducing the trends of available piezometric and salinity measurements reasonably well for a long period of data 1973-2009 (37 years). Thus, the new model might constitute and advance tool for water and environmental planning and management in the area. However, using this model as a starting point, further efforts might be done considering a higher resolution parameterization of K that would support a better matching of salinity data, and would lead to a more plausible and realistic model. Nonetheless, other effects as up-coning and dynamic piezometric levels should be studied and characterized for more precise calibrations.
Results show the important impact of variable density flow effects on the calibration and model outputs. The average annual saltwater intrusion is estimated as 1.67 hm3/yr, compared to the much lower previous estimation of 0.65 hm3/yr for the historical period 1973-2009. This result confirms the progressive decrease of intrusion mainly due to the decrease of wells abstraction―see Figure 14.
The discharge to the wetland Prat de Cabanes is another important output of this research. The obtained estimation, 1.68 hm3/yr, is a more plausible estimation than any of the previous figures given by other authors. Besides, the representation of the wetland in the model is much more accurate than before―126 discretization blocks distributed in three layers. Thus, the model constitutes a robust tool to simulate future changes of external stresses over the aquifer and to assess possible impacts in the wetland.
Although the available external stresses data might be improved, the main external inflow to study and model more accurately remains to be the inflow from the underlying Cretaceous formation that represents lateral recharge from Maestrazgo aquifer. The new model provides a result not very different from the previous model; this fact makes the current results more plausible and reliable. However, this component of the water budget is three times the infiltration, and comparable to the average wells abstraction in 1973-2009. During the most recent years it is even larger―by 50%―than total pumping abstractions. This situation calls for further research regarding the estimation of this component, including the study of the water budget of neighboring hydrogeological formations.
Among potential and useful applications of this model it should be considered the simulation of future climate change scenarios in this geographical area. Besides the fact of existing sea water level rise predictions, the area of study is located in a geographical region where the impacts of climate change in water resources are expected to be important. This will have a significant impact―to be assessed―in infiltration and on the recharging inflows from the Maestrazgo aquifer.
Acknowledgements
We acknowledge the data and previous model reports provided by Instituto Geológico y Minero de España (IGME), as well as the data and helpful comments provided by Professor Ignacio Morell (UniversitatJaume I, Spain) and Dr. Arianna Renau-Pruñonosa.
Cite this paper
IgnacioSanz-Garrido,José E.Capilla, (2015) Assessment of Saltwater Intrusion and Discharges to a Wetland with a 3D Transient Variable Density Flow Model: The Coastal Plane Oropesa-Torreblanca Aquifer, Spain. Journal of Water Resource and Protection,07,749-768. doi: 10.4236/jwarp.2015.79062
References
- 1. Webb, M.D. and Howard, K.W.F. (2011) Modeling the Transient Response of Saline Intrusion to Rising Sea-Levels. Ground Water, 49, 560-569. http://dx.doi.org/10.1111/j.1745-6584.2010.00758.x
- 2. Todd, D.K. (1974) Salt-Water Intrusion and Its Control. Journal of American Water Works Association, 66, 180-187.
- 3. Chang, S.W. and Clement, T.P. (2012) Experimental and Numerical Investigation of Saltwater Intrusion Dynamics in Flux-Controlled Groundwater Systems. Water Resources Research, 48, 1-10.
http://dx.doi.org/10.1029/2012WR012134 - 4. Lahm, T.D., Bair, E.S. and Vander Kwaak, J. (1998) Role of Salinity-Derived Variable-Density Flow in the Displacement of Brine from a Shallow, Regionally Extensive Aquifer. Water Resources Research, 34, 1469-1480. http://dx.doi.org/10.1029/98WR00316
- 5. Capilla, J.E., Gómez-Hernández, J.J. and Sahuquillo, A. (1998) Stochastic Simulation of Transmissivity Fields Conditional to Both Transmissivity and Piezometric Head Data—3. Application to the Culebra Formation at the Waste Isolation Pilot Plan (WIPP), New Mexico, USA. Journal of Hydrology, 207, 254-269. http://dx.doi.org/10.1016/S0022-1694(98)00138-3
- 6. Morell, I. (1985) Caracterización hidroquímica de la intrusión marina en la Plana de Oropesa-Torreblanca (Castellón). Ph.D. Thesis, University of Granada, Granada.
- 7. Instituto Geológico y Minero de Espana, IGME (2009) Estudio piloto para el cálculo de descargas ambientales al mar en las masas de agua subterránea costeras de la provincia de Castellón (Cuenca del Júcar). Madrid, Spain. http://info.igme.es/SIDIMAGENES/140000/557/140557_0000003.PDF
- 8. Renau-Prunonosa, A. (2012) Nueva herramienta para la gestión de las aguas subterráneas en acuíferos costeros. Volumen ecológico de remediación (VER). Metodología y aplicación a la Plana de Oropesa-Torreblanca (MASub 080.110). Ph.D. Thesis, Universidad Jaume I, Castellón de la Plana. www.tdx.cat
- 9. RAMSAR Convention Bureau (1990) Directory of Wetlands of International Importance Sites Designated for the List of Wetlands of International Importance. http://www.ramsar.org/
- 10. Directive 2009/147/EC of the European Parliament and of the Council of 30 November 2009 on the Conservation of Wild Birds. http://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32009L0147
- 11. Quereda, J. (1975) El Pla de l’Arc: Benlloch y Cabanes. In: Millars: Revista del Colegio Universitario de Castellón de la Plana, Volume 2, Col·legi Universitari de Castelló, Castelló, 95-125.
http://www.raco.cat/index.php/MillarsCUCP/index - 12. Quereda, J. (1985) Geomorfologia. In: La provincia de Castellón de la Plana. Tierras y gentes, Caja de Ahorros y Monte de Piedad de Castellón, Castellón, 25-47.
- 13. SegarraiJulve, X. (1985) Marjaleria de Cabanes-Torreblanca. Treballs de la Societat Catalana de Biologia, 37, 131-236.
- 14. Castanyi Alvaro, J. (2004) El carricerín real (Acrocephalus melanopogon) en el P.N. del Prat de Cabanes—Torreblanca. Ph.D. Thesis, Universitat de Valencia, Valencia. www.tdx.cat
- 15. Alfonso, C. (2002) Entrevista a Francisco Cabezas Calvo-Rubio, Subdirector General de Planificación Hidrológica: Evaluación Ambiental Estratégica del PHN. Revista Ambienta, Volume 9.
www.revistaambienta.es - 16. Renau-Prunonosa, A., Morell, I., Pulido, D. and Mateu J. (2014) Ecological Remediation Volume (ERV) in Coastal Aquifers Affected by Seawater Intrusion. Methodology and Application in the Oropesa-Torreblanca Plain (Spain). In: Mathematics of Planet Earth: Proceedings of the 15th Annual Conference of the International Association for Mathematical Geosciences, Springer, Heidelberg, 333-337.
- 17. Jucar River Basin Authority (2015) www.chj.es.
- 18. Sanz, I. (2013) Modelo matemático para la caracterización e investigación de la interfaz salina del acuífero de la Plana litoral de Oropesa-Torreblanca (Unidad hidrogeológica 8.11). Master’s Thesis, Technical University of Valencia, Valencia. http://hdl.handle.net/10251/37381
- 19. Harbaugh, A.W., Banta, E.R., Hill, M.C. and McDonald, M.G. (2000) MODFLOW 2000, the US Geological Survey Modular Ground-Water Model: User Guide to Modularization Concepts and the Ground-Water Flow Process. USGS Open File Report 00-92, USGS, USA.
- 20. Guo, W.X. and Langevin Christian, D. (2002) User’s Guide to SEAWAT: A Computer Program for Simulation of Three-Dimensional Variable-Density Groundwater Flow. USGS Techniques of Water Resources Investigations Book 6 Chapter A7, USA.
- 21. Chiang, W.-H. and Kinzelbach, W. (2003) 3D-Groundwater Modeling with PMWIN: A Simulation System for Modeling Groundwater Flow and Pollution. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-05549-6 - 22. Zheng, C. and Wang, P. (1999) MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. US Army Corps of Engineers, Washington, DC.
- 23. Baxter, G.P. and Wallace, C.C. (1916) Changes in Volume upon Solution in Water of Halogen Salts of Alkali Metals. American Chemical Society Journal, 38, 70-105. http://dx.doi.org/10.1021/ja02258a010















