Journal of Software Engineering and Applications
Vol.7 No.1(2014), Article ID:42203,6 pages DOI:10.4236/jsea.2014.71007
Generalized α-Entropy Based Medical Image Segmentation
1Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt; 2Mathematics Department, Faculty of Science, Taif Univesity, Taif, KSA.
Email: samy.technik@gmail.com, sayedquantum@yahoo.co.uk
Copyright © 2014 Samy Sadek, Sayed Abdel-Khalek. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Samy Sadek, Sayed Abdel-Khalek. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 19th, 2013; revised December 18th, 2013; accepted December 26th, 2013
KEYWORDS
α-Entropy; Cell Image; Entropic Image Segmentation
ABSTRACT
In 1953, Rènyi introduced his pioneering work (known as α-entropies) to generalize the traditional notion of entropy. The functionalities of α-entropies share the major properties of Shannon’s entropy. Moreover, these entropies can be easily estimated using a kernel estimate. This makes their use by many researchers in computer vision community greatly appealing. In this paper, an efficient and fast entropic method for noisy cell image segmentation is presented. The method utilizes generalized α-entropy to measure the maximum structural information of image and to locate the optimal threshold desired by segmentation. To speed up the proposed method, computations are carried out on 1D histograms of image. Experimental results show that the proposed method is efficient and much more tolerant to noise than other state-of-the-art segmentation techniques.
1. Introduction
Instinctively, image segmentation is the process of dividing an image into different regions such that each region is homogeneous while not the union of any two adjacent regions. An additional requirement would be that these regions have a correspondence to real homogeneous regions belonging to objects in the scene [1]. Image segmentation is an elementary and significant component in many applications such as image analysis, pattern recognition, medical diagnosis and currently in robotic vision. However, it is one of the most difficult and challenging tasks in image processing, and it determines the quality of the final results of the image analysis. The recent developments in Digital Mammography (DM), Magnetic Resonance Imaging (MRI), Computed Tomography (CT), and other diagnostic imaging techniques provide physicians with high resolution images which have significantly assisted the clinical diagnosis. These up-to-date technologies not only have a recognizably increased knowledge of normal and diseased anatomy for medical research but also become a significant part in diagnosis and treatment planning [2].
Due to the increasing number of medical images, taking advantage of computers to facilitate the processing and analyzing of this huge number of images has become indispensable. Especially, algorithms for the delineation of anatomical structures and other regions of interest are a key component in assisting and automating specific radiological tasks. These algorithms, named image segmentation algorithms, play a fundamental role in many medical imaging applications such as the quantification of tissue volumes [3,4], diagnosis [5], localization of pathology [6,7], study of anatomical structure [8,9], treatment planning [10], partial volume correction of functional imaging data [11], and computer integrated surgery [12-14]. Techniques for carrying out segmentations vary broadly depending on some factors such as specific application, imaging modality, etc. For instance, the segmentation of brain tissue has different requirements from the segmentation of the liver [15]. General imaging artifacts such as noise, partial volume effects, and motion can also have significant consequences on the performance of segmentation algorithms. Additionally, each imaging modality has its own idiosyncrasies with which to contend.
There is currently no single segmentation technique that gives satisfactory results for each medical image.
Since the pioneering work by Shannon [16,17] in 1948, entropy appears as an attention-grabbing tool in many areas of data processing. In 1953, Rènyi [8] introduced a wider class of entropies known as 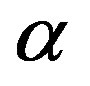 -entropies. The functionalities of
-entropies. The functionalities of  -entropies share the major properties of Shannon’s entropy. Moreover, the
-entropies share the major properties of Shannon’s entropy. Moreover, the  -entropies can be easily estimated using a kernel estimate. This makes their use attractive in many areas of image processing [18-20]. In this paper, we propose an efficient entropic technique for segmenting cell images which utilizes generalized Rènyi entropy. Our work for cell image segmentation has a relatively good performance in comparison to other related state-of-the-art techniques [21,22].
-entropies can be easily estimated using a kernel estimate. This makes their use attractive in many areas of image processing [18-20]. In this paper, we propose an efficient entropic technique for segmenting cell images which utilizes generalized Rènyi entropy. Our work for cell image segmentation has a relatively good performance in comparison to other related state-of-the-art techniques [21,22].
The outline of this paper is as follows. The next section discusses the generalized form of α-entropies especially generalized Rényi entropy. The proposed entropic segmentation method is explained in Section 3. Section 4 is to present the experimental results that validate the use of the proposed method. Advantages of our method and concluding remarks are outlined in Section 5.
2. Entropy of Generalized Distributions
Entropy has first appeared in thermodynamics as an information theoretical concept which is intimately related to the internal energy of the system. Then it has applied across physics, information theory, mathematics and other branches of science and engineering [9]. When given a system whose exact description is not precisely known, the entropy is defined as the expected amount of information needed to exactly specify the state of the system, given what we know about the system.
Suppose 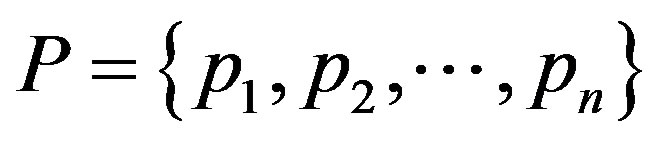 be a finite discrete probability distribution that satisfies these conditions
be a finite discrete probability distribution that satisfies these conditions
 and
and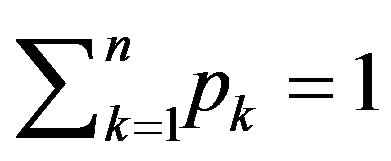 . The amount of uncertainty of the distribution
. The amount of uncertainty of the distribution , is called the entropy of the distribution, P. The Shannon entropy of the distribution, P, a measure of uncertainty and denoted by
, is called the entropy of the distribution, P. The Shannon entropy of the distribution, P, a measure of uncertainty and denoted by ), is defined as
), is defined as
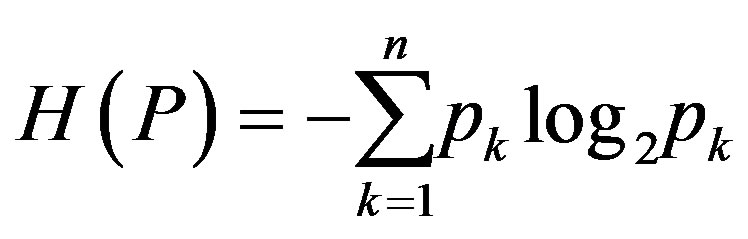 (1)
(1)
It should be noted that the Shannon entropy given by Equation (1) is additive, i.e. it satisfies the following relation:
 (2)
(2)
for any two distributions  and
and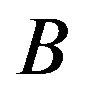 . Equation (2) states one of the most important properties of entropy, namely, its additivity: the entropy of a combined experiment consisting of the performance of two independent experiments is equal to the sum of the entropies of these two experiments. The formalism defined by Equation (1) has been shown to be restricted to the Boltzmann-GibbsShannon (BGS) statistics. However, for nonextensive systems, some kind of extension appears to become necessary. Rènyi entropy, which is useful for describing the nonextensive systems, is defined as Entropic segmentation for noisy mammography image.
. Equation (2) states one of the most important properties of entropy, namely, its additivity: the entropy of a combined experiment consisting of the performance of two independent experiments is equal to the sum of the entropies of these two experiments. The formalism defined by Equation (1) has been shown to be restricted to the Boltzmann-GibbsShannon (BGS) statistics. However, for nonextensive systems, some kind of extension appears to become necessary. Rènyi entropy, which is useful for describing the nonextensive systems, is defined as Entropic segmentation for noisy mammography image.
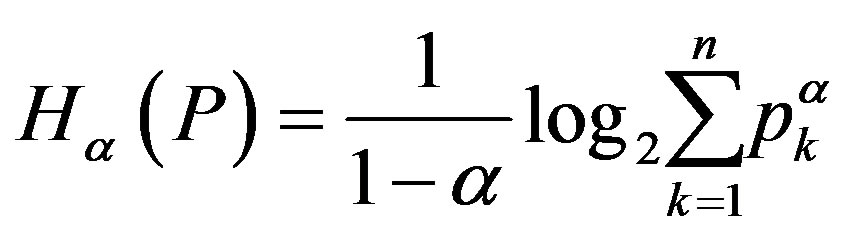 (3)
(3)
where 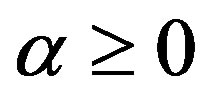 and
and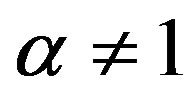 . The real number
. The real number  is called an entropic order that characterizes the degree of nonextensivity. This expression reduces to Shannon entropy in the limit
is called an entropic order that characterizes the degree of nonextensivity. This expression reduces to Shannon entropy in the limit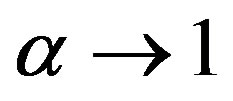 . We shall see that in order to get the fine characterization of Rànyi entropy, it is advantageous to extend the notion of a probability distribution, and define entropy for the generalized distributions. The characterization of measures of entropy (and information) becomes much simpler if we consider these quantities as defined on the set of generalized probability distributions.
. We shall see that in order to get the fine characterization of Rànyi entropy, it is advantageous to extend the notion of a probability distribution, and define entropy for the generalized distributions. The characterization of measures of entropy (and information) becomes much simpler if we consider these quantities as defined on the set of generalized probability distributions.
Suppose  be a probability space that is,
be a probability space that is,  an arbitrary nonempty set, called the set of elementary events, and P a probability measure, that is, a non-negative and additive set function for which
an arbitrary nonempty set, called the set of elementary events, and P a probability measure, that is, a non-negative and additive set function for which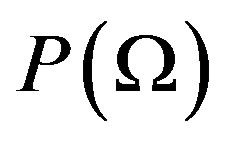 . Let us call a function
. Let us call a function 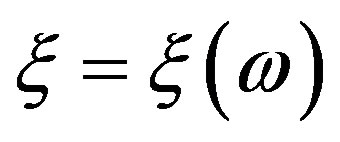 which is defined for
which is defined for , where
, where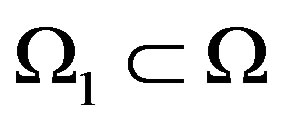 . If
. If 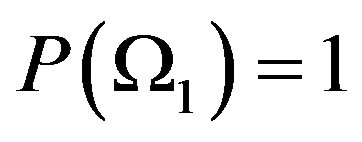 we call
we call  an ordinary (or complete) random variable, while if
an ordinary (or complete) random variable, while if
 we call
we call  an incomplete random variable. Evidently, an incomplete random variable can be interpreted as a quantity describing the result of an experiment depending on chance which is not always observable, only with probability
an incomplete random variable. Evidently, an incomplete random variable can be interpreted as a quantity describing the result of an experiment depending on chance which is not always observable, only with probability . The distribution of a generalized random variable is called a generalized probability distribution. Thus a finite discrete generalized probability distribution is simply a sequence
. The distribution of a generalized random variable is called a generalized probability distribution. Thus a finite discrete generalized probability distribution is simply a sequence 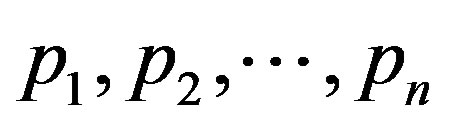 of nonnegative numbers such that setting
of nonnegative numbers such that setting 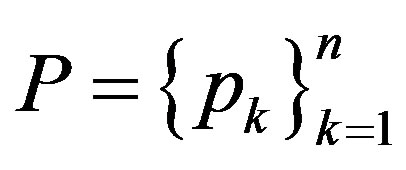 and taking
and taking
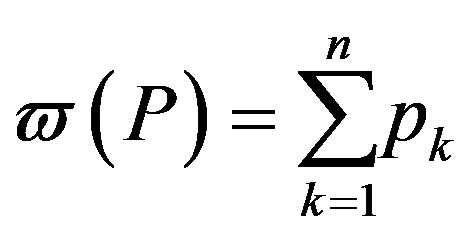 (4)
(4)
where 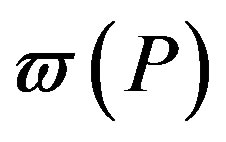 is the weight of the distribution and
is the weight of the distribution and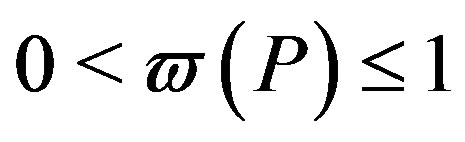 . A distribution that has a weight less than 1 will be called an incomplete distribution. Now, using Equation (3) and Equation (4), the Rànyi entropy for the generalized distribution can be written as
. A distribution that has a weight less than 1 will be called an incomplete distribution. Now, using Equation (3) and Equation (4), the Rànyi entropy for the generalized distribution can be written as
 (5)
(5)
Note that Rànyi entropy has a nonextensive property for statistical independent systems, defined by the following pseudo additivity entropic formula
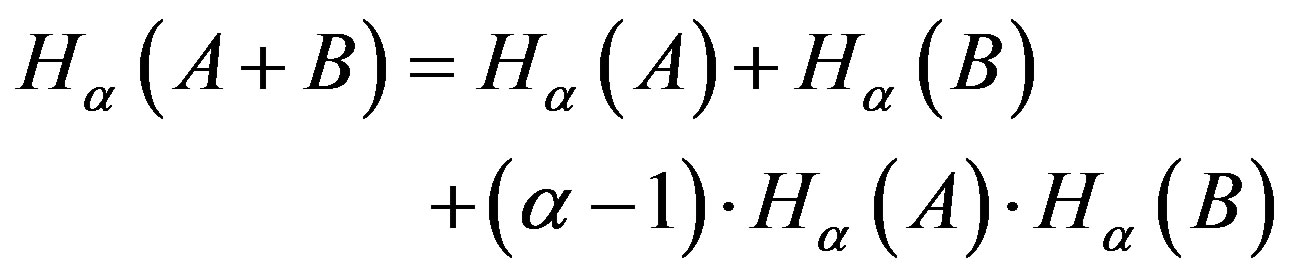 (6)
(6)
3. Suggested Methodology
Image segmentation problem is considered to be one of the most holy grail challenges of computer vision field especially when done for noisy images. Consequently it has received considerable attention by many researchers in computer vision community. There are many approach for image segmentation, however, these approach are still inadequate. In this work, we propose an entropic method that achieves the task of segmentation in a novel way. This method not only overcomes image noise, but also utilizes time and memory optimally. This wisely happens by the advantage of using the Rànyi entropy of generalized distributions to measure the structural information of image and then locate the optimal threshold depending on the postulation that the optimal threshold corresponds to the segmentation with maximum structure (i.e., maximum information content of the distribution). The implementation steps of the proposed segmentation method are shown in the block diagram of Figure 1. The following sections outline in detail the process behind each step.
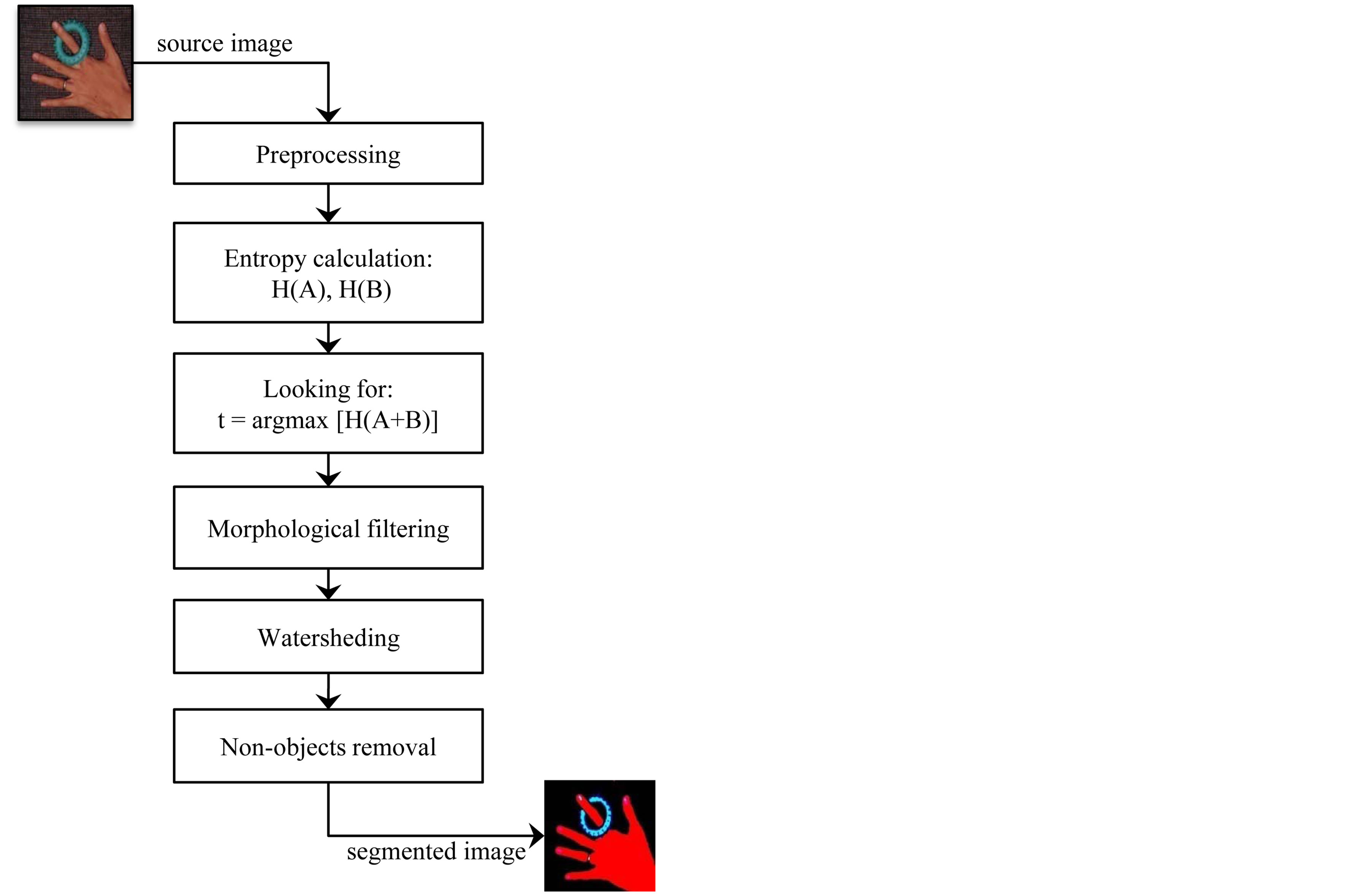
Figure 1. Block diagram of the proposed segmentation method.
3.1. Preprocessing
Preprocessing ultimately aims at improving the image in ways that increase the opportunity for success of the other ulterior processes [17,23]. In this step, we apply a Gaussian filter to the input image prior to any process in order to reduce the amount of noise in an image.
3.2. Entropies Calculation
Suppose  be the probability distribution for the image. At the threshold,
be the probability distribution for the image. At the threshold,  this distribution is divided into two sub distributions; one for the foreground (class f) and the other for the background (class b) given by
this distribution is divided into two sub distributions; one for the foreground (class f) and the other for the background (class b) given by 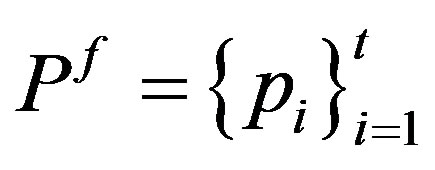 and
and 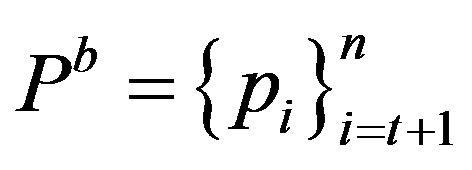 respectively. Thus, the generalized Rànyi entropies for the two distributions as functions of
respectively. Thus, the generalized Rànyi entropies for the two distributions as functions of  are given as
are given as
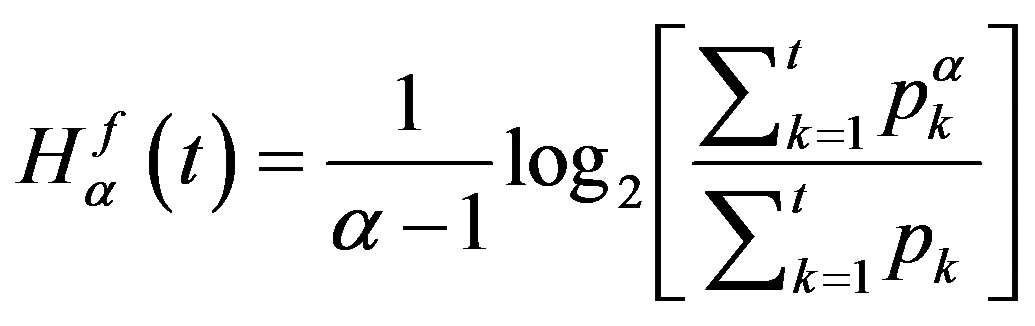 (7)
(7)
 (8)
(8)
3.3. Image Thresholding
Thresholding is the most often used technique to distinguish objects from background. In this step an input image is converted by threshed into a binary image so that the objects in the input image can be easily separated from the background. To get the desired optimum threshold value t*, we have to maximize the total entropy,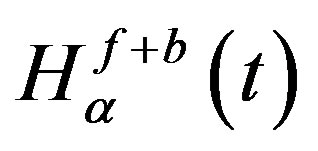 . When the function
. When the function 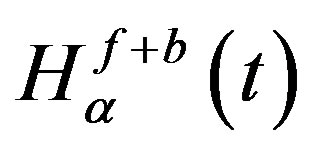 is maximized, the value of parameter
is maximized, the value of parameter  that maximizes the function is believed to be the optimum threshold value [24]. Mathematically, the problem can be formulated as
that maximizes the function is believed to be the optimum threshold value [24]. Mathematically, the problem can be formulated as
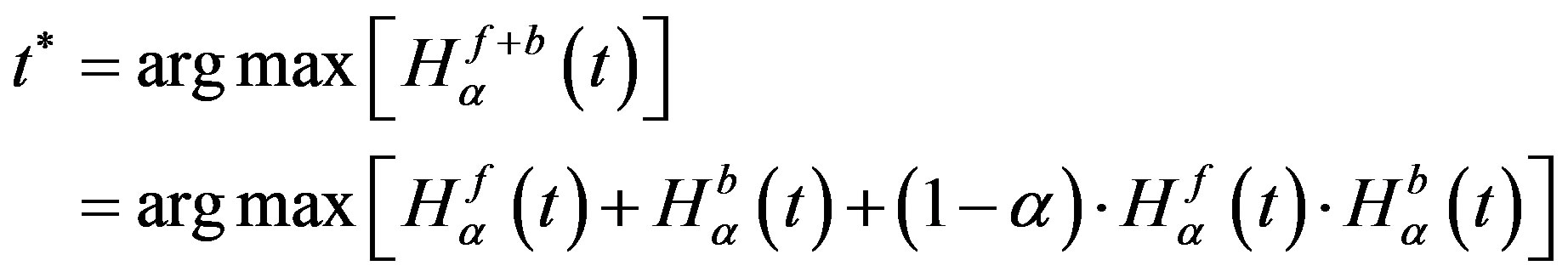 (9)
(9)
3.4. Morphology-Based Operations
In image processing, dilation, erosion, closing and opening are all well-known as morphological operations. In this step we aim at improving the results of the previous thresholding step. Due to the inconsistency within the color of objects, the resulting binary image perhaps includes some holes inside. By applying the closing morphological operation, we can get rid of the holes form the binary image. Furthermore Opening operation with small structure element can be used to separate some objects that are still connected in small number of pixels [25,26].
3.5. Overlapping Cancelation
In this step we attempt to remove the overlapping between objects that perhaps happened through extensively applying the previous morphological operations. To perform this, we first get the Euclidean Distance Transform (EDT) of the binary image. Then we apply the wellknown watershed algorithm [27,28] on the resulting EDT image. The EDT ultimately converts the binary image into one where each pixel has a value equal to its distance to the nearest foreground pixel. The distances are measured in Euclidean distance metric. The peaks of the distance transform are assumed to be in the centers of the objects. Then the overlapping objects can be yet easily separated.
3.6. Non-Objects Removal
This step helps in removing incorrect objects according to the object size. Sizes of objects are measured in comparison to the total size of image. Each tiny noise object of size less than a predefined minimum threshold can be discarded. Also each object whose size is greater than the maximum threshold size can be removed as well. Note that thresholds of size used herein are often dependent on the application, and so they are considered as user-defined data.
4. Experimental Results
In this section, the results of the proposed approach are presented. First to investigate the proposed approach for image segmentation we began by different image histograms. Each of these histograms describes the “objects” and the “background”. Additionally, to verify the benefit of using the generalized Rènyi entropy, we have tried using another formula of entropy (e.g. Tsallis entropy) which is given by
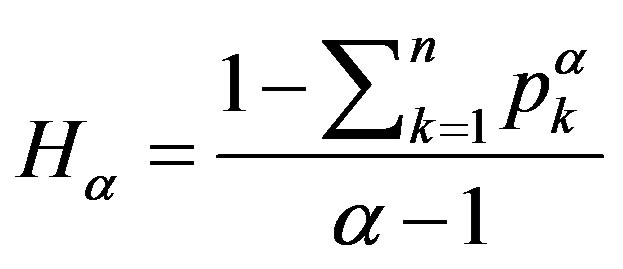 (10)
(10)
The results of segmentation have testified to the higher efficiency of our entropic segmentation approach especially when generalized Rènyi entropy is used.
In Figure 2, an image of a mammogram showing breast cancer with a bright region (tumefaction) surrounded by a noisy region. The histogram roughly exemplifies an unimodal distribution of the graylevel values. The proposed entropic method will look for regions with uniform distribution in order to find the maximum entropy. This will regularly take place at the peak limit. It is well-known that segmenting this type of images is typically a challenging task. However the proposed method could performed well when applied on this type of images. Additionally, segmentation results in the figure show that using generalized Rènyi entropy is better than using Tsallis entropy.
Figure 3 shows another example of our segmentation method. We present an image of a medical domain with a spatial background scattering noise; a stained brain cell that shows branching of cell dendrites-fibers that receive input from other brain cells. Several values of 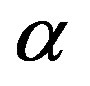 are experimented. But the superior segmentation results has been obtained at
are experimented. But the superior segmentation results has been obtained at .
.
In Figure 4, we show the segmentation results of the proposed method on a sample of color medical images. In this example the images are segmented with 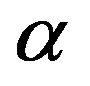 equal to 0.8.
equal to 0.8.
5. Conclusion
In this paper, we introduced a new method for cell image segmentation based on generalized 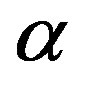 -entropy. The proposed method has achieved the task of segmentation in a novel way. This method has been shown to provide good results in most cases and perform well when applied to noisy cell images. The experimental results show that using generalized Rènyi formalism of entropy is more viable than using Tsallis counterpart in segmentating cell image. The chief advantages of the method are its high
-entropy. The proposed method has achieved the task of segmentation in a novel way. This method has been shown to provide good results in most cases and perform well when applied to noisy cell images. The experimental results show that using generalized Rènyi formalism of entropy is more viable than using Tsallis counterpart in segmentating cell image. The chief advantages of the method are its high
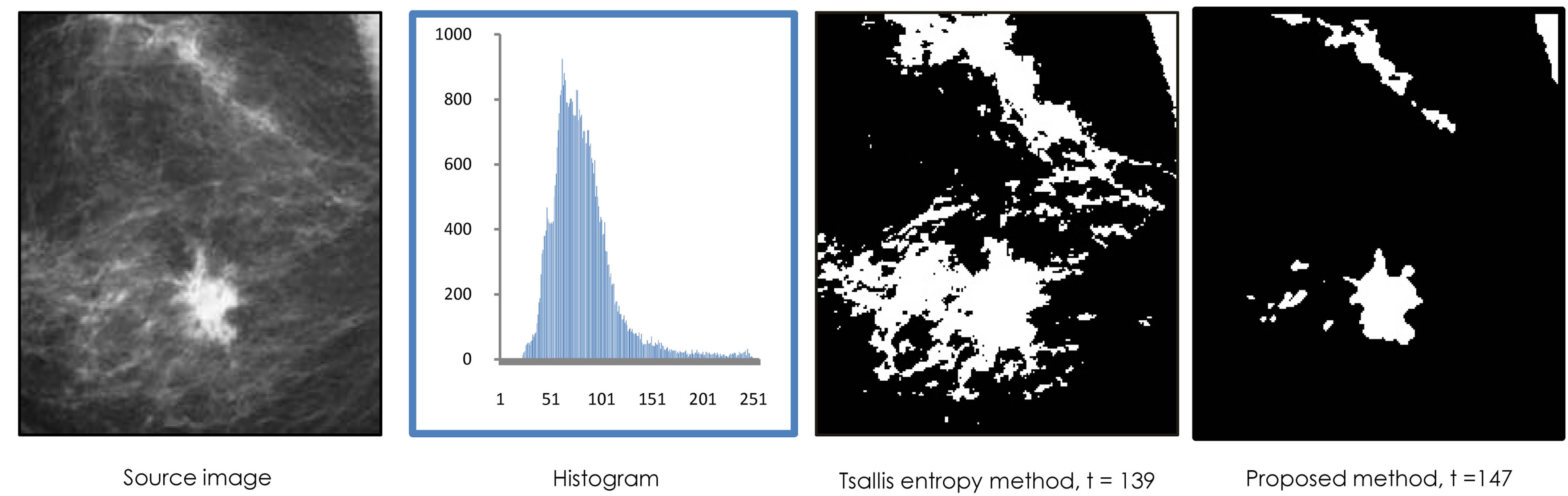
Figure 2. Entropic segmentation for noisy mammography image.
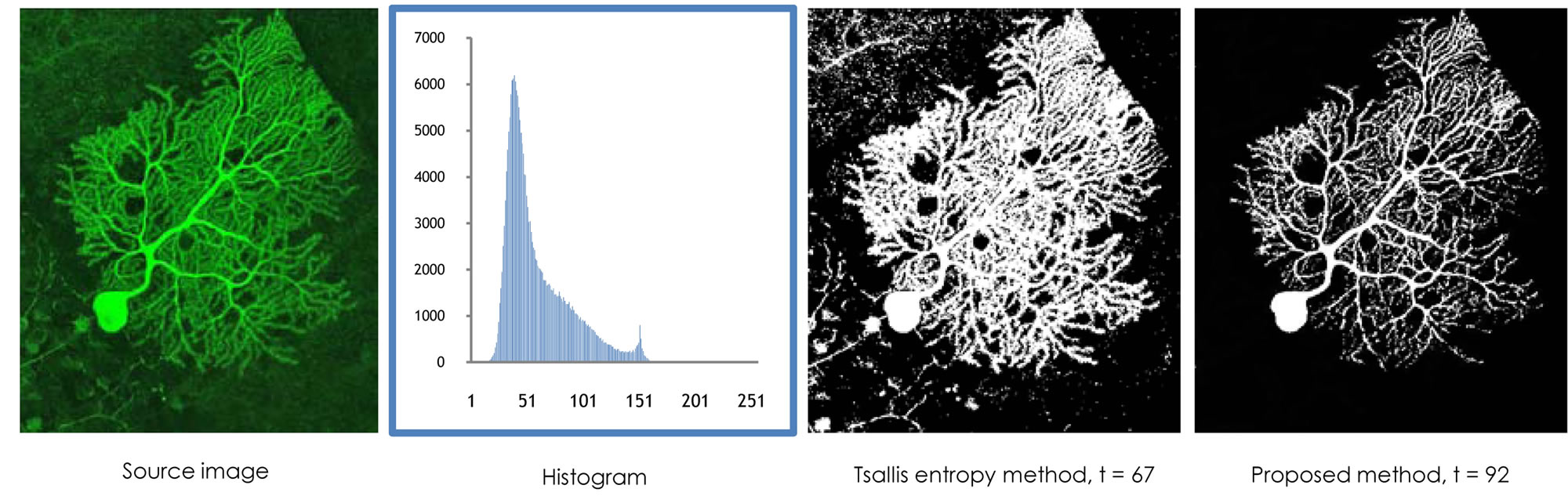
Figure 3. Entropic segmentation for a brain cell image with a spatial noise around.
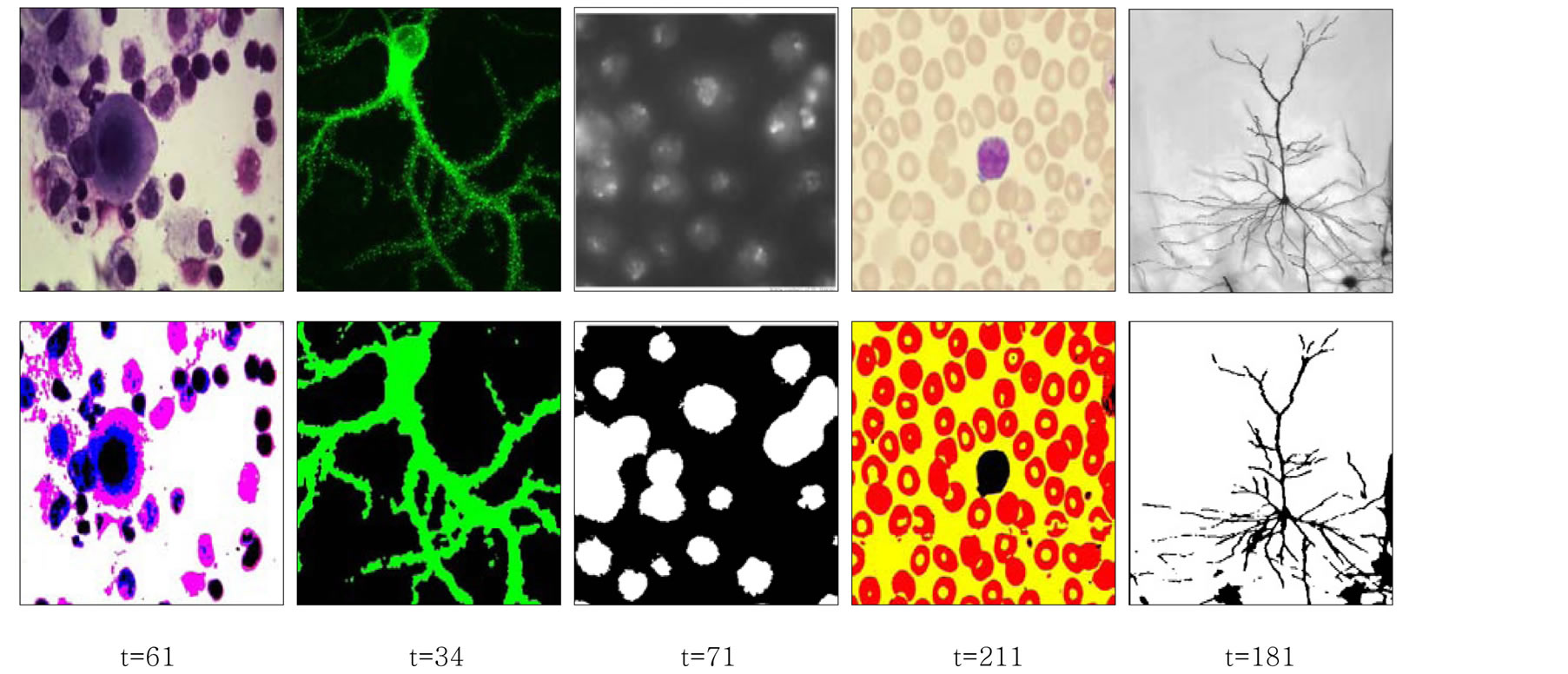
Figure 4. Results of the proposed segmentation method for a sample of test images.
rapidity and its tolerance to image noise.
REFERENCES
- M. Albuquerque, I. A. Esquef and A. R. Gesualdi, “Image Thresholding Using Tsallis Entropy,” Pattern Recognition Letters, Vol. 25, No. 9, 2004, pp. 1059-1065. http://dx.doi.org/10.1016/j.patrec.2004.03.003
- P.-L. Bazin and D. L. Pham, “Homeomorphic Brain Image Segmentation with Topological and Statistical Atlases,” Medical Image Analysis, Vol. 12, No. 5, 2008, pp. 616- 625. http://dx.doi.org/10.1016/j.media.2008.06.008
- P.-L. Bazin and D. L. Pham, “Topology Correction of Segmented Medical Images Using a Fast Marching Algorithm,” Programs in Biomedicine, Vol. 88, No. 2, 2007, pp. 182-290. http://dx.doi.org/10.1016/j.cmpb.2007.08.006
- J. C. Carter, D. C. Lanham, G. Bibat, S. Naidu and W. E. Kaufmann, “Selective Cerebral Volume Reduction in Rett Syndrome: A Multiple Approach MRI Study,” American Journal of Neuroradiology, Vol. 29, No. 3, 2008, pp. 436-441. http://dx.doi.org/10.3174/ajnr.A0857
- R. C. Gonzalez and R. E. Woods, “Digital Image Processing Using Matlab,” 2nd Edition, Prentice Hall, Inc., Upper Saddle River, 2003.
- W. E. L. Grimson, G. J. Ettinger, T. Kapur, M. E. Leventon and W. M. Wells, “Utilizing Segmented MRI Data in Image-Guided Surgery,” International Journal of Pattern Recognition and Artificial Intelligence, Vol. 11, No. 8, 1997, pp. 1367-1397. http://dx.doi.org/10.1142/S0218001497000639
- V. S. Khoo, D. P. Dearnaley, D. J. Finnigan, A. Padhani, S. F. Tanner and M. O. Leach, “Magnetic Resonance Imaging (MRI): Considerations and Applications in Radiotheraphy Treatment Planning,” Radiotherapy Oncology, Vol. 42, No. 1, 1997, pp. 1-15. http://dx.doi.org/10.1016/S0167-8140(96)01866-X
- S. M. Larie and S. S. Abukmeil, “Brain Abnormality in Schizophrenia: A Systematic and Quantitative Review of Volumetric Magnetic Resonance Imaging Studies,” Journal of Psychiatry, Vol. 172, 1998, pp. 110-120.
- I. Levner and H. Zhang, “Classification-Driven Watershed Segmentation,” EEE Transactions on Image Processing, Vol. 16, No. 5, 2007, pp. 1437-1445. http://dx.doi.org/10.1109/TIP.2007.894239
- M. A. Mofaddel and S. Sadek, “Adult Image Content Filtering: A Statistical Method Based on Multi-Color Skin Modeling,” IEEE International Symposium on Signal Processing and Information Technology (ISSPIT’10), Luxor, 2010, pp. 366-370. http://dx.doi.org/10.1109/ISSPIT.2010.5711812
- A. Rényi, “On a Theorem of P. Erdǒs and Its Application in Information Theory,” Mathematica, Vol. 1, 1959, pp. 341-344.
- S. M. Resnick, D. L. Pham, M. A. Kraut, A. B. Zonderman and C. Davatzikos, “Longitudinal MRI Studies of Older Adults: A Shrinking Brain,” Journal of Neuroscience, Vol. 23, No. 8, 2003, pp. 3295-3301.
- S. Sadek, A. Al-Hamadi, M. Elmezain, B. Michaelis and U. Sayed, “Human Activity Recognition Using Temporal Shape Moments,” IEEE International Symposium on Signal Processing and Information Technology (ISSPIT’10), Luxor, 2010, pp. 79-84. http://dx.doi.org/10.1109/ISSPIT.2010.5711729
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “A Fast Statistical Approach for Human Activity Recognition,” International Journal of Intelligence Science (IJIS), Vol. 2, No. 1, 2012, pp. 9-15.
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “An Efficient Method for Real-Time Activity Recognition,” Proceedings of the International Conference on Soft Computing and Pattern Recognition (SoCPaR’10), Paris, 2010, pp. 7-10.
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “An Image Classification Approach Using Multilevel Neural Networks,” Proceedings of IEEE International Conference on Intelligent Computing and Intelligent Systems (ICIS’09), Shanghai, 2009, pp. 180-183.
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “Face Detection and Localization in Color Images: An Efficient Neural Approach,” Journal of Software Engineering and Applications (JSEA), Vol. 4, No. 12, 2011, pp. 682-687. http://dx.doi.org/10.4236/jsea.2011.412080
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “Human Action Recognition via Affine Moment Invariants,” 21st International Conference on Pattern Recognition (ICPR’12), Tsukuba Science City, 2012, pp. 218-221.
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “Human Action Recognition: A Novel Scheme Using Fuzzy Log-Polar Histogram and Temporal Self-Similarity,” EURASIP Journal on Advances in Signal Processing, 2011. http://dx.doi.org/10.1155/2011/540375
- S. Sadek, A. Al-Hamadi, A. Wannig, B. Michaelis and U. Sayed, “A New Approach to Image Segmentation via Fuzzification of Rènyi Entropy of Generalized Distributions. Proceedings of International Conference on Image, Signal and Vision Computing (ICISVC’09), Singapore, 2009, pp. 598-603.
- S. Sadek, A. Al-Hamadi, B. Michaelis and U. Sayed, “A Robust Neural System for Objectionable Image Recognition,” IEEE International Conference on Machine Vision (ICMV’09), 2009, pp. 32-36.
- S. Sadek, M. A. Mofaddel and B. Michaelis, “Multicolor Skin Modeling with Application to Skin Detection,” Journal of Computations & Modelling, Vol. 3, No. 1, 2013, pp. 153-167.
- C. E. Shannon and W. Weaver, “The Mathematical Theory of Communication,” University of Illinois Press, Urbana, 1949.
- W. Tatsuaki and S. Takeshi, “When Nonextensive Entropy Becomes Extensive,” Physica A, Vol. 301, No. 1-4, 2001, pp. 284-290. http://dx.doi.org/10.1016/S0378-4371(01)00400-9
- P. Taylor, “Invited Review: Computer Aids for DecisionMaking in Diagnostic Radiology—A Literature Review,” British Journal of Radiology, Vol. 68, No. 813, 1995, pp. 945-957. http://dx.doi.org/10.1259/0007-1285-68-813-945
- D. Tosun, M. E. Rettmann, X. Han, X. Tao, C. Xu, S. M. Resnick and J. L. Prince, “Cortical Surface Segmentation and Mapping,” NeuroImage, Vol. 23, No. 1, 2004, pp. S108-S118. http://dx.doi.org/10.1016/j.neuroimage.2004.07.042
- C. Tsallis, S. Abe and Y. Okamoto, “Nonextensive Statistical Mechanics and Its Applications,” Series Lecture Notes in Physics, Springer, Berlin, 2001.
- A. J. Worth, N. Makris, V. S. Caviness and D. N. Kennedy, “Neuroanatomical Segmentation in MRI: Technological Objectives,” International Journal of Pattern Recognition and Artificial Intelligence, Vol. 11, No. 8, 1997, pp. 1161-1187. http://dx.doi.org/10.1142/S0218001497000548

