Journal of Software Engineering and Applications
Vol. 5 No. 6 (2012) , Article ID: 19856 , 7 pages DOI:10.4236/jsea.2012.56049
The Graphical Method for Decision of Restitution Coefficient and Its Applications
![]()
Department of Electronic, School of Information and Communications Technology, Mongolian University of Science and Technology, Ulaanbaatar, Mongolia.
Email: Hurlee77@yahoo.com, {enkhzul, amartuvshin, sukhbat}@sict.edu.mn
Received March 28th, 2012; revised April 24th, 2012; accepted May 3rd, 2012
Keywords: ODE; Restitution Coefficient; Virtual Body; Virtual Body’s Position and Velocity; Assumption of Virtual Body
ABSTRACT
In this paper we present a graphical method for decision of restitution coefficient based on ODE. To simulate and illustrate our proposed method and efficient characteristics that demonstrate for two colliding bodies we used MatLab. In simulation to approach to the real case we used an assumption of additional virtual body’s position and velocity for characterizing material of the body which is involved to express the restitution coefficient. The graphic animation program is developed based on ODE for the computer simulation of the proposed graphical method. Additionally, we determined this new characteristic for some sport game balls such as basketball, volleyball, etc.
1. Introduction
Computer graphic animation developers have been still concentrating on increasing the “reality” of the graphic representation as in the real world. During the last few years many attractive works of efficient-and-popular for robotics simulation applications are based on Open Dynamic Engine (ODE) [1]. Since the most popular dynamic engines are licensed at a high cost, this makes it impossible for independent researchers to improve their algorithm in specific areas. Fortunately, there are powerful open source and high performance physical engines such as ODE, for simulating rigid body dynamics.
Collision detection and real performance of a collision have a significant role for rigid body simulation and animation. The cardinal parameter in the collision is the restitution coefficient. However in ODE, there is no approach to establish the restitution coefficient. We aimed to model the restitution coefficient for ODE. In ODE the restitution coefficient is assumed as constant for each collision contact, and named bouncing coefficient [2]. The classic approximation of restitution coefficient is based on assumption of body as with damping element, and such a model is mass-spring-dashpot system [3-5]. To compute simply a collision for a dynamic engine machine, the restitution coefficient is approximated by velocity time and penetration depth [6,7].
We used assumption of additional virtual body’s position and velocity for characterizing material of the body which is involved to express the restitution coefficient. It gives possibility to calculate automatically restitution coefficient of two bodies while they are in a collision. Figure 1 shows the assumption of virtual and real bodies.
Furthermore, we attempted to establish virtual characteristics for individual bodies in order to use it for calculating restitution coefficient in ODE environment. To complete this goal we choose five kinds of sport game balls; basketball ball, volleyball ball, soccer (football) ball, tennis ball and table tennis (ping-pong) ball. Official sport associations of these sport games have their own standards for testing balls that we can use these data to calculate the characteristics of virtual body [8].
2. Ball Standard According to Association Rule
We use some sport game balls for approximation of restitution coefficient them. Sport game associations, such as of basketball, volleyball, tennis etc., have their official rules and standards for ball, especially for testing. Each association sets the bouncing test standard for the ball by considering floor as steel, additionally sets the initial dropping height and bouncing min height or min/max height [8]. From these parameters, we can calculate restitution coefficient of balls. Therefore, it gives us to establish virtual characteristics of a ball [2].
According to standards from official associations, we can have physical information such as circumference,

Figure 1. The assumption of virtual body and real body in ODE.
weight, air pressure and material of a ball, and testing information such as initial height and bouncing height. For example, FIFA’s (The Fédération International de Football Association) size-5 ball has to weigh 420 g - 445 g, and its circumference has to be 68.5 cm - 69.5 cm. For testing the bounce of a ball, association sets the bounce standard as initial dropping height is 2 m, bouncing height is in a range between 120 cm - 165 cm [9- 11].
There are been also many research works in which is validated with real measurement data of a bouncing ball [11-14].
3. Open Dynamic Engine (ODE)
The Open Dynamics Engine (ODE) is a free, industrial quality library for simulating the articulated rigid body dynamics. Proven applications include simulating ground vehicles, legged creatures, and moving objects in virtual environments. It is fast, flexible, robust and has built-in collision detection. ODE is being developed by Russell Smith with help from several contributors since 2001. ODE is good for simulating articulated rigid body structures. An articulated structure is created when rigid bodies of various shapes are connected together with joints of various kinds. ODE is designed to be used in interactive or real-time simulation, and uses a highly stable integrator, so that the simulation errors should not grow out of control [2].
ODE has hard contacts and has a built-in collision detection system [15].
4. Colliding Contact in ODE
This section introduces a velocity computing method after collision in the ODE. Since two bodies have colliding contact, there exist impulse J. Therefore, velocity difference, after collision could be simply derived by following [16].
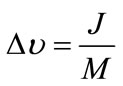 (1)
(1)
where Du is velocity difference, M is mass of body. Impact is along axis which is perpendicular to the colliding surface. Hence, impulse could be expressed as below [16]:
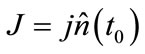 (2)
(2)
where 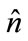 is a normal vector which is perpendicular to the colliding surface.
is a normal vector which is perpendicular to the colliding surface.
Figure 2 shows relation between two relative velocities ( and
and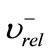 ), before and after collision, is a restitution coefficient e.
), before and after collision, is a restitution coefficient e.
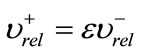 (3)
(3)
The restitution coefficient e must be satisfied to 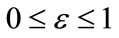 If
If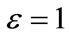 , then
, then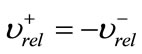 , and the collision is perfectly bouncy; in particular, no kinetic energy is lost. At the other end of the spectrum,
, and the collision is perfectly bouncy; in particular, no kinetic energy is lost. At the other end of the spectrum, 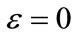 result in
result in  and a maximum of kinetic energy is lost [9].
and a maximum of kinetic energy is lost [9].
General motion equations after collisions is
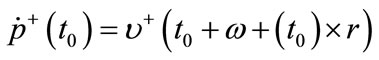 (4)
(4)
where r is fixed vector in body space, u+, w+ and 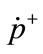 are the linear velocity, rotational velocity and a general velocity of a particle after collision. By considering Equations (1), (2) and (4) for each of bodies, and substituting them to the Equation (3), we derive impulse function in terms of the relative velocity before impact and restitution coefficient [16].
are the linear velocity, rotational velocity and a general velocity of a particle after collision. By considering Equations (1), (2) and (4) for each of bodies, and substituting them to the Equation (3), we derive impulse function in terms of the relative velocity before impact and restitution coefficient [16].

Figure 2. Two bodies collision at the contacting point.
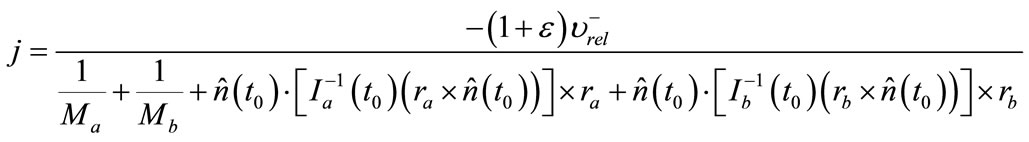 (5)
(5)
Here Ma and Mb are masses, Ia and Ib are inertia tensors of the bodies, ra and rb are relative radius of the contact points of each body respect to mass of center [16].
Detailed derivation is in the reference [10]. Using this value and Equation (1), we simply determine the velocity after collision for each collision. In ODE, the restitution coefficient is given as constant for each collision. For the reality, this coefficient should be expressed close to the real world value.
5. The Graphical Method for Decision of Restitution Coefficient
Physically, the restitution coefficient of bodies, which are in a collision, depends on their material property. In the real world, there is an energy loss, at least for generating sound, after impact of two bodies. This requires a proper assumption of modeling for the collision body in a computer graphic animation and robot simulation [17].
Our assumption for approximation of restitution coefficient consists of two parameters. First, we assume that each body (A1 and B1) has their own virtual body (A2 and B2) and inside them (Figure 3). This virtual body’s surface has definite distance (xA and xB) from the real body’s surface (Figure 3(a)). Next, virtual bodies A2 and B2 move to the contact point with the predetermined constant velocities  and
and  for individual body, whenever two real bodies get in a collision at the contact point C1 (Figure 3(b)). The virtual body, with faster velocity and closer distance to the contacting point C1 reaches to the real body surface (in other words contacting point C1), at first (Figure 3(c)). Then it penetrates to the opposite body and consequently changes its velocity (
for individual body, whenever two real bodies get in a collision at the contact point C1 (Figure 3(b)). The virtual body, with faster velocity and closer distance to the contacting point C1 reaches to the real body surface (in other words contacting point C1), at first (Figure 3(c)). Then it penetrates to the opposite body and consequently changes its velocity (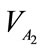 ) to the opposite virtual body’s velocity (
) to the opposite virtual body’s velocity (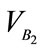 ). It moves forward until virtual bodies reach each other at the virtual body contact point C2. Thereafter, we calculate time T which is spent time by the motion of virtual bodies until they have a contact each other by using Equation (6).
). It moves forward until virtual bodies reach each other at the virtual body contact point C2. Thereafter, we calculate time T which is spent time by the motion of virtual bodies until they have a contact each other by using Equation (6).
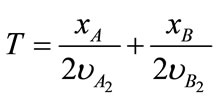 (6)
(6)
where xA and xB are the positions of the virtual bodies, while 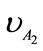 and
and  are velocities of the virtual bodies. We can use this time value to determine the restitution coefficient (7).
are velocities of the virtual bodies. We can use this time value to determine the restitution coefficient (7).
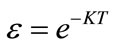 (7)
(7)
where K is a real constant.
The combination of virtual body’s position and velocity implies that there is a loss of kinetic energy in a collision.
The position extent of distance between virtual body surface and real body surface x is opposite proportionality with the restitution coefficient value e. The velocity of virtual body u is a proportional relation to the restitution coefficient e. If assuming that body has no affection to distraction of kinetic energy, the virtual body surface and real body surface coincide (x = 0) therefore, there is no virtual velocity for the body (u = 0). If body is assumed with a great dissipation of kinetic energy then distance should be away from the surface of real body and virtual body velocity should be slow. Then it gives great value of T time.
Figure 4 shows relation between restitution coefficient e and time T which is spent by virtual bodies to reach at the contact point C2.
We show relation characteristics between restitution coefficient and virtual parameters in Figures 5 and 6 which are obtained by Equations (6) and (7).
Therefore we can choose virtual parameters by using characteristics that demonstrate the restitution coefficient for graphical animation of real bodies.
6. Determining Virtual Body Characteristics for Sport Game Balls
Official associations of sport games have their own standards to test the ball quality that whether ball’s quality is adequate for using in a game or not. We collect these data from official sites of the games and the Table 1 shows the physical characteristics and testing characteristics for the balls. We choose the five kinds of sport games:
• Basketball;
• Volleyball;
• Soccer (Football);
• Tennis;
• Table tennis (Ping-Pong).
By assuming initial velocity in an initial height we can calculate velocities just before colliding and just after colliding. The initial velocity is zero when we drop ball test. Therefore, we can calculate final velocity as ball reaches floor.
 (8)
(8)
If we substitute (8) to (3), we find restitution coefficient as follows.
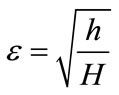 (9)
(9)
where H is initial dropping height and h is final height after bouncing when ball’s velocity reaches zero.
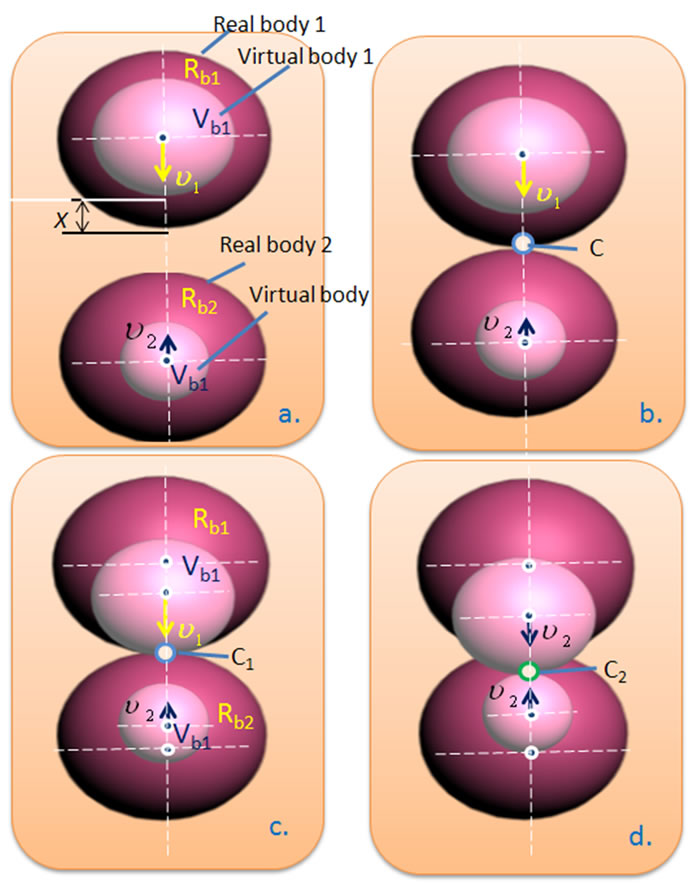
Figure 3. An assumption of virtual body in the collision. (a) Two real bodies A1 and B1 move towards each other with their own velocities  and
and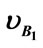 .Virtual bodies A1 and B1 have their own initial distance xA and xB; b) Two bodies are in a collision at the contact point C1; c) Since real bodies are in a collision, virtual body A2 penetrates to surface of the real body
.Virtual bodies A1 and B1 have their own initial distance xA and xB; b) Two bodies are in a collision at the contact point C1; c) Since real bodies are in a collision, virtual body A2 penetrates to surface of the real body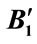 , but changes its velocity to the virtual body B2’s velocity
, but changes its velocity to the virtual body B2’s velocity ; d) Two virtual bodies move towards each other with same velocity until they reach at the contact point C2 of virtual bodies.
; d) Two virtual bodies move towards each other with same velocity until they reach at the contact point C2 of virtual bodies.
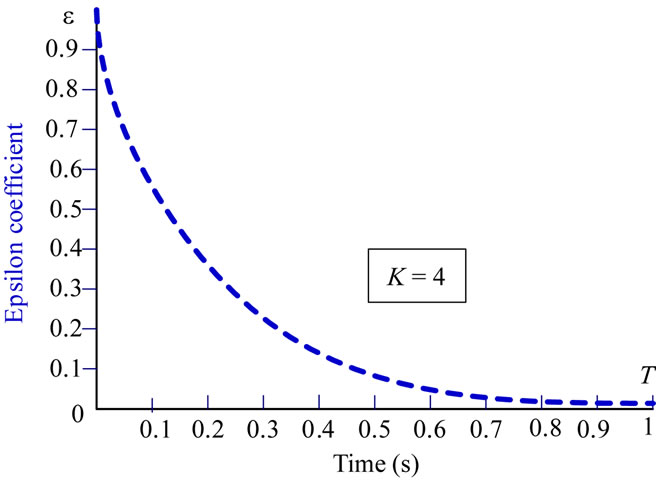
Figure 4. The relation between restitution coefficient ε and the collision time T of virtual bodies.
The floor has to be steel for the testing, this gives us opportunity to determine virtual characteristics for a ball. Under this condition, we can assume one body (steel floor) as it has no motion, and we can change (6) as follows:
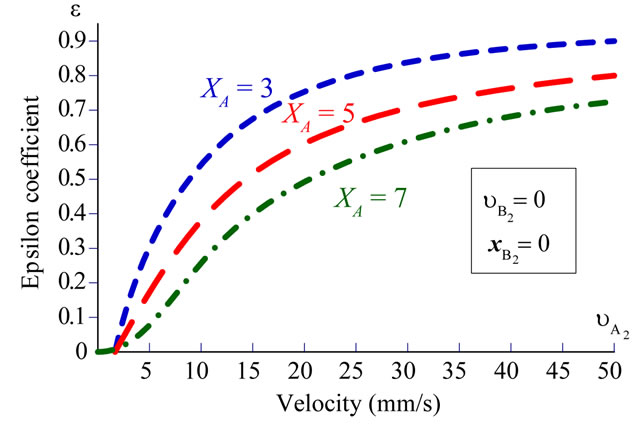
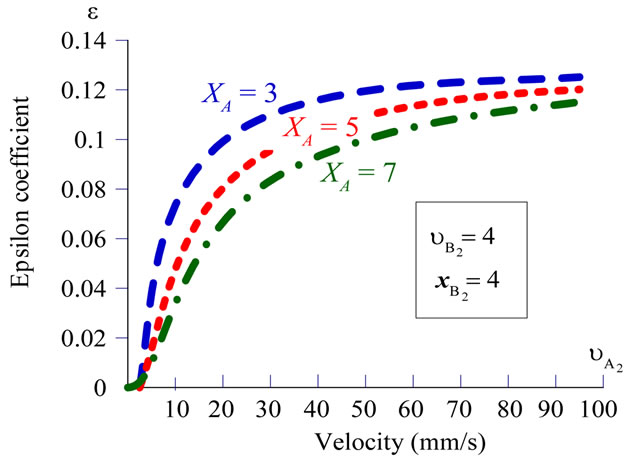
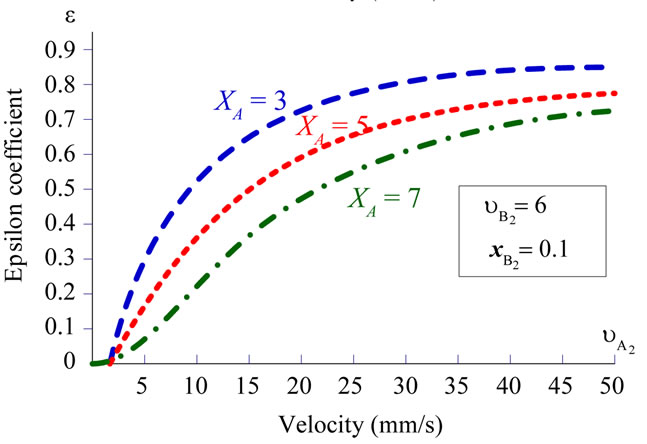

Figure 5. Here are the characteristics that demonstrate the relate to the velocity as for two colliding bodies. We give constant values to the position (xB) and velocity (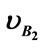 ) of the virtual body B2. and three different values to the position (xA) of the another virtual body A2 and vary the velocity
) of the virtual body B2. and three different values to the position (xA) of the another virtual body A2 and vary the velocity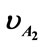 .
.
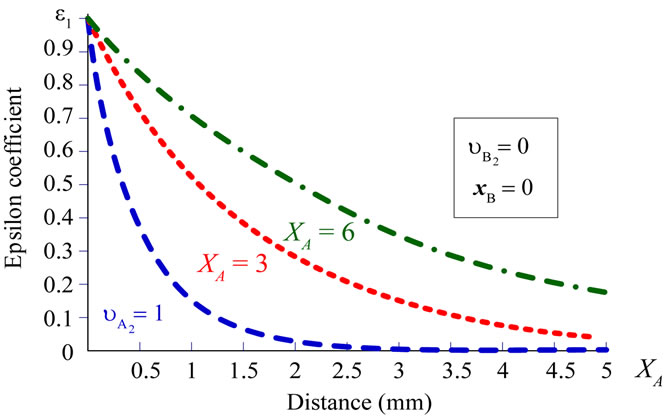
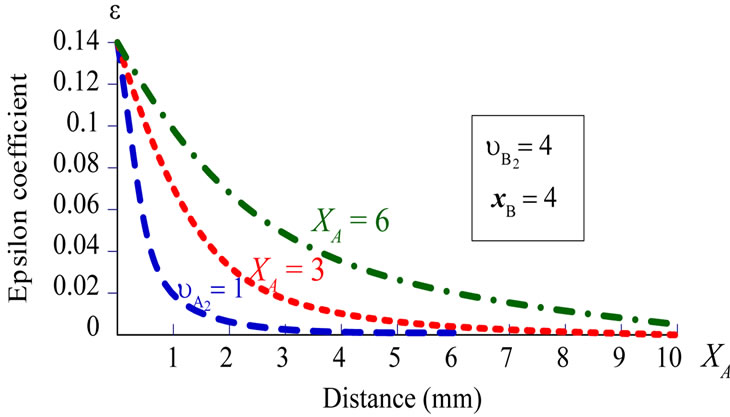
Figure 6. Here are the characteristics that demonstrate the restitution coefficient relate to the distance as for two colliding bodies. We give constant values to the position (xB) and velocity (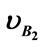 ) of the virtual body B2, and three different values to the velocity (
) of the virtual body B2, and three different values to the velocity (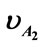 ) of the another virtual body A2 and vary the position xA.
) of the another virtual body A2 and vary the position xA.
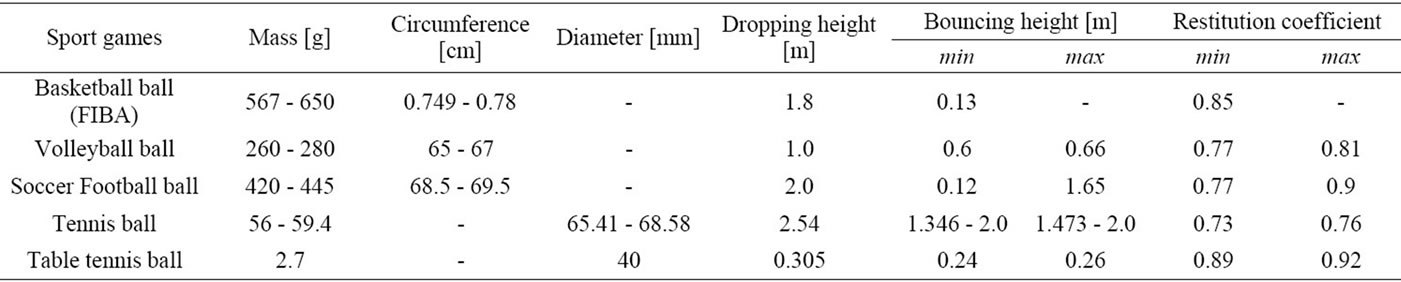
Table 1. Physical and testing characteristics of sport game balls.
 (10)
(10)
where xB is the virtual body’s position of the ball while 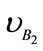 is virtual velocity of the ball.
is virtual velocity of the ball.
Figure 7 shows the relation between virtual velocity and virtual position of basketball ball. The basketball ball bouncing test in ODE environment is depicted in Figure 8.
In the Table 2 we show parameters of selection for virtual velocity and virtual position by using Equations (7) and (10) for determine the restitution coefficient of some real balls in ODE.
7. Implementation in ODE
Previous section deals with an approximation for the restitution coefficient in the collision. In this section we discuss updating ODE with the restitution coefficient.
ODE creates a World for the dynamics calculation and Space for the collision detection. An object has two attributes which are a body for dynamics and a geometry for collision detection. A geometry attribute is defined by “Geom” structure on the simulation. Therefore we need to add information of virtual body to the structure “Geom” for the approximation. Two variables which are related to the position (x) and velocity (u) of the virtual body are added to the “Geom” structure. In ODE when collision occurs, ODE collision function approximates the restitution coefficient by using Equation (7) and its application

Figure 7. The relation between virtual velocity and position of basketball ball.

Figure 8. The measuring of the basketball ball bouncing in ODE.
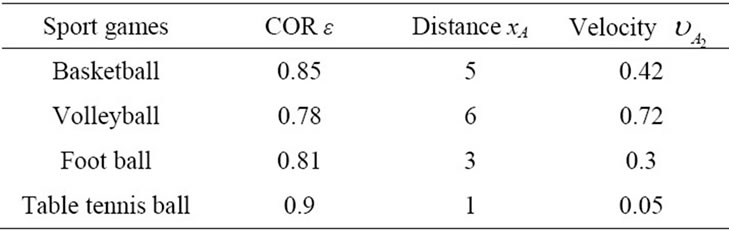
Table 2. Sample of selection for virtual velocity and virtual position of sport game balls.

Figure 9. Ball implementation in ODE with approximated restitution coefficient.
creates by using near Call back() function with o1 and o2 arguments for simulation [18]. In simulation the collision coefficient is calculated following algorithm.
For every contact
………………………….
Enable Contact Bounce Parameter
Calculate Time constant T
Calculate
………………………….
This algorithm helps us to decide restitution coefficient for collision between many bodies related to their property of material. Figure 9 is the simulation results of bouncing bodies.
8. Conclusion
Open Dynamic Engine (ODE) is powerful and useful well-introduced physics engine for computer animation and robot simulation. Unfortunately, in ODE, restitution coefficient is assigned by the user for every collision. Even though, the restitution coefficient depends on many physical factors of each body which are in a collision, we have attempted to approximate this coefficient for ODE by using assumption of the virtual body, and its position and velocity. This assumption gives us better opportunity to approximate the restitution coefficient. We also, implemented this approximation to the ODE and received good result. In order to test the simple approximation for restitution coefficient we use sport game balls as models that has its standards by official associations. So, we can see that the simple approximation is valid for collision, especially, for balls.
9. Acknowledgements
This work was supported by project of School of Information and Communications Technology, Mongolian University of Science and Technology.
REFERENCES
- D. Evan and J. Hsu, “Extending Open Dynamics Engine for Robotics Simulation,” Springer-Verlag, Berlin, 2010.
- http://opende.sourceforge.net
- S. Faik and H. Witteman, “Modeling of Impact Dynamics Literature Survey,” International ADAMS Users’ Conference, Orlando, 17-19 June 2000, pp. 3-10.
- T. Schwager and T. Pöschel, “Coefficient of Restitution and Linear-Dashpot Model Revisited,” Granular Matter, Vol. 9, No. 6, 2007, pp. 465-469. doi:10.1007/s10035-007-0065-z
- M. Nagurka and S. G. Huang, “A Mass-Spring-Damper Model of a Bouncing Ball,” Proceedings of the 2004 American Control Conference, Boston, 30 June-2 July 2004, pp. 499-504.
- X. Zhang and L. Vu-Quoc, “Modeling the Dependence of the Coefficient of Restitution on the Impact Velocity in Elasto-Plastic Collisions,” International Journal of Impact Engineering, Vol. 27, No. 3, 2002, pp. 317-341. doi:10.1016/S0734-743X(01)00052-5
- D. W. Marhefka and D. E. Orin, “Simulation of Contact Using a Nonlinear Damping Model,” Proceedings of IEEE International Conference on Robotics and Automation, Minneapolis, 22-28 April 1996, pp. 1662-1668.
- As Approved by FIBA Central Board, “Official Basketball Rules 2010,” San Juan, 2010, pp. 2-81.
- C. J. Lu and M. C. Kuo, “Coefficients of Restitution Based on a Fractal Surface Model,” Journal of Applied Mechanics, Vol. 70, No. 3, 2003, pp. 339-345. doi:10.1115/1.1574063
- J. Bender and A. Schmitt, “Constraint-Based Collision and Contact Handling Using Impulses,” Proceedings of the 19th International Conference on Computer Animation and Social Agents, Geneva, 5-7 June 2006, pp. 3-11.
- http://www.njp.org
- D. J. Wagg, “A Note on Coefficient of Restitution Models including the Effects of Impact Induced Vibration,” Journal of Sound and Vibration, Vol. 300, No. 3-5, 2007, pp. 1071-1078. doi:10.1016/j.jsv.2006.08.030
- H. F. Frank, “Determination Coefficient of Restitution Based on Model Test Data,” Journal of Applied Mechanics, Vol. 70, 2003, pp. 339-345.
- T. Lens, “Simulation of Dynamics and Realistic Contact Forces for Manipulators and Legged Robots with High Joint Elasticity,” 15th International Conference on Advanced Robotic, Tallinn, 20-23 June 2011, pp. 34-41.
- R. A. LaFarge and C. Lewis, “Contact Force Modeling between Non Convex Objects Using a Nonlinear Damping Model,” International ADAMS User Conference, Ann Arbor, 9-10 June 1998, pp. 1-8.
- http://www.pixar.com/aboutpixar/research/pbm2001
- Ts. Khurelbaatar and B. Luubaatar, “The Graphical Method for Decision of Restitution Coefficient in Open Dynamic Engine,” Ubiquitous Robots and Ambient Intelligence, Busan, 24-27 November 2010, pp. 63-64.
- http://opened.sourceforge.net/wiki/index.php

