Journal of Software Engineering and Applications
Vol. 5 No. 3 (2012) , Article ID: 18297 , 12 pages DOI:10.4236/jsea.2012.53023
Evaluation of Stiffened End-Plate Moment Connection through Optimized Artificial Neural Network
![]()
School of Civil Engineering, University of Tehran, Tehran, Iran.
Email: *mghassem@ut.ac.ir
Received December 13th, 2011; revised January 16th, 2012; accepted February 7th, 2012
Keywords: End-Plate Moment Connection; Finite Element Method; Artificial Neural Network; Sensitivities Analysis; Genetic Algorithm
ABSTRACT
This study involves the development of an analytical model for understanding the behavior of the extended, stiffened end-plate moment connections with eight high strength bolts. Modeling of the connection as an assemblage of finite elements (FE) used for load deformation analysis, with material, and contact nonlinearities are developed. Results from the FE mathematical model are verified with results from the ANSYS computer program as well as with the test results. Sensitivity and feasibility studies are carried out. Significant geometry and force related variables are introduced; and by varying the geometric variables of the connections within a practical range, a matrix of test cases is obtained. Maximum end-plate separation, maximum bending stresses in the end-plate, and the forces from the connection bolts for these test cases are obtained. From the FE analysis, a database is produced to collect results for the artificial neural network analysis. Finally, salient features of the optimized Artificial Neural Network (ANN) via Genetic Algorithm (GA) analysis are introduced and implemented with the aim of predicting the overall behavior of the connection.
1. Introduction
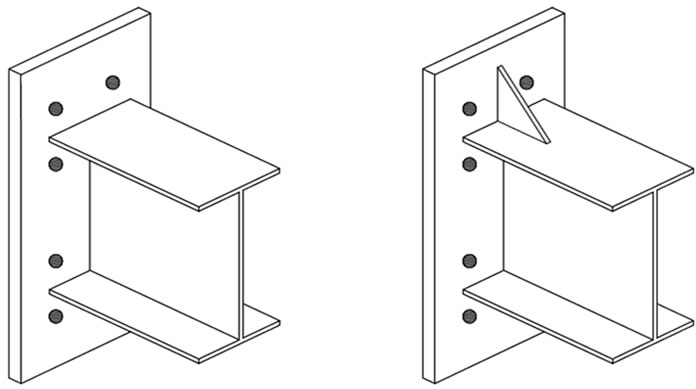
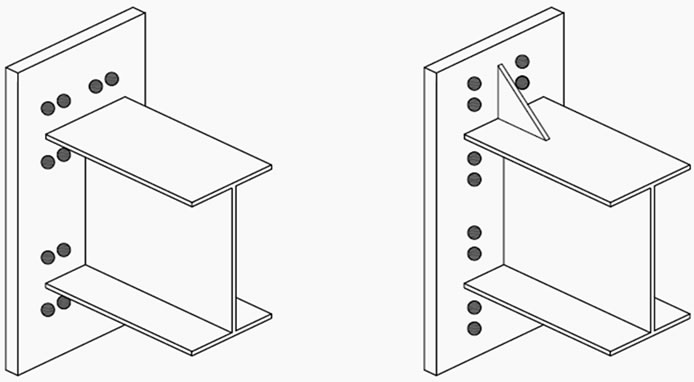
End-plate moment connections (shown in Figure 1) are becoming more popular and are used extensively in steel frames for buildings due to its well behavior and simplicity of fabrication and erection. Figure 1(a) shows an unstiffened end-plate moment connection, of which the end-plate thickness can be reduced by adding a stiffener above the tension flange. This is referred to as a stiffened end-plate (Figure 1(b)). For heavier beams, the required bolt size becomes larger than can be practically used for installation. In these cases the required bolt area could be distributed over a larger number of bolts as shown in Figure 2.
There is extensive published literature available on extended end-plate moment connections. Krishnamurthy (l978a) developed the linearly elastic FE methodology specifically for the analysis of unstiffened, four-bolt extended, end-plates (Figure 1(a)) [1]. Based on his extensive analytical study of end-plates, as well as a series of experimental tests, Krishnamurthy developed the design procedure found in the AISC Manual of Steel Construction (1980) [2]. Krishnamurthy (1978 a, b) also investigated the behavior of stiffened end-plates using four bolts in the tension region (Figure l(b)) [1,3]. The tension region was modeled as a tee hanger using the FE method. Ghassemieh et al. (1983) developed the nonlinear FE methodology specifically for the analysis of stiffened eight bolt extended end-plates (Figure 2(b)) [4]. In his study, the tension region was modeled as a tee hanger using the nonlinear FE method. From the results of the analysis of practical geometric dimensions, Ghassemieh developed prediction equations that characterized the connection behavior [4]. Murray and Kukreti (1988) modified the design equations developed by Ghassemieh et al. (1983) and they proposed a new, simplified design procedure which is found in the AISC Manual of Steel Construction (1989) [4-6]. Kukreti et al. (1990) compared the results of the extended end-plate tests with the prediction equations developed from regression analyses of many end-plate cases [7]. Bahaari and Sherbourne (1996) used ANSYS, a general FE program, to evaluate the characteristics of the steel bolted end-plate connection and they validated the proposed computer model by comparing their results with the results obtained by them from prototype experiments [8]. Sumner (2003) proposed a unified design method for this connection and then experimentally examined the connections designed by the proposed method, he concluded that this connection can
 (a) (b)
(a) (b)
Figure 1. Extended end-plate connections for light beams (a) Unstiffened; (b) Stiffened.
 (a) (b)
(a) (b)
Figure 2. Extended end-plate connections for heavy beams (a) Unstiffened; (b) Stiffened.
generate the required stiffness, ductility and strength for the seismic loading [9]. Gang et al. (2004) reported the results of several tests on bolted end-plate connections and analyzed the connections by finite element method; the design steps of the extended end-plate moment connections were discussed [10]. Yongjiu et al. (2007) developed a new theoretical model to evaluate the momentrotation relationship for stiffened, extended end-plate connections and verified their proposed model by test results [11].
The aforementioned studies, and others, used timeconsuming experimentation to explore the behavior and try to develop the prediction equations for the extended end-plate moment connections. While some researchers such as Srouji et al. (1983), Bose et al. (1997), and Broderick and Thomson (2002) studied the behavior of similar connections and most developed detailed finite element method models for flush end-plate moment connections and compared their analysis results with experimental results [12-14].
In this paper, predicting the general behavior of the end-plate moment connection subjected to monotonic loading, shown in Figure 2(b), based on a FE methodology and through optimized artificial neural network, is presented. Development of relations of the behavior of large capacity stiffened extended end-plate moment connection with two bolt rows below and above the beam flanges (Figure 2(b)) based on material, geometric, and contact nonlinear FE analyses of connection region are presented. The accuracy of the FE model and its results are verified by using experimentally obtained displacement and bolt force data [4]. Also, a test matrix with twenty five theoretical specimens is introduced by varying the pertinent geometrical variables of the end-plate connection within its practical ranges. All those cases are analyzed using the developed FE model. The results obtained from the analysis consisted of the end-plate separation, stresses in the end-plate, and near bolt and far bolt forces. In order to develop a model that characterizes the connection behavior, from the result of the FE analyses, a database is formed to be used by the optimized Artificial Neural Network (ANN) using Genetic Algorithm (GA). From the results of the FE analysis stored in the data base, the genetic algorithm based on a feed forward neural network is applied in order to model the behavior of the end-plate moment connection. Only ASTM A36 steel material and ASTM A325 bolt material are considered in this study.
2. Finite Element Model
In this study the FE model is used to model the tension region of the stiffened end-plate with eight bolts. The configuration of the FE model for the connection and its details used in most analyses is shown in Figure 3. Since a plane of symmetry exists along a section through the beam web, by applying the T hanger analogy, one-quarter of the connection region including end-plate and beam flange is modeled. The most critical part of the model, the end-plate, is idealized using the 33-degrees-of-freedom three-dimensional sub-parametric elements (with 9 degrees of freedom used internally). For the stiffener, two dimensional sub-parametric quadrilateral and triangular elements are used, while for the tee-stem, two-dimensional, four-noded rectangular hybrid plane stress elements are used. The weld connecting the tee-stem with the end-plate is modeled using the previously mentioned three-dimensional elements. Other welds are modeled using four noded rectangular two dimensional elements. The effect of the bolt shanks, bolt heads and bolt nuts on the end-plate concerning the elongations, constraints and necking actions are carefully considered in the model. The complicated interaction behavior between the surface of end-plate and column flange are modeled with the node to node contact criteria.
The end-plate and bolt material behavior are described by trilinear stress-strain curves as shown in Figure 4 with the initial slope of the curve being taken as the elastic modulus of the material. To check yielding, the effective strain, εeff, for an element was evaluated using von-
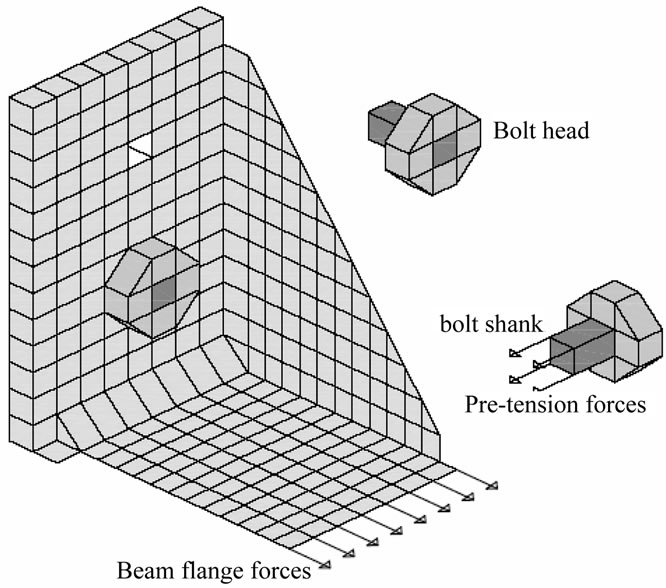
Figure 3. Finite element quarter model of the connection.
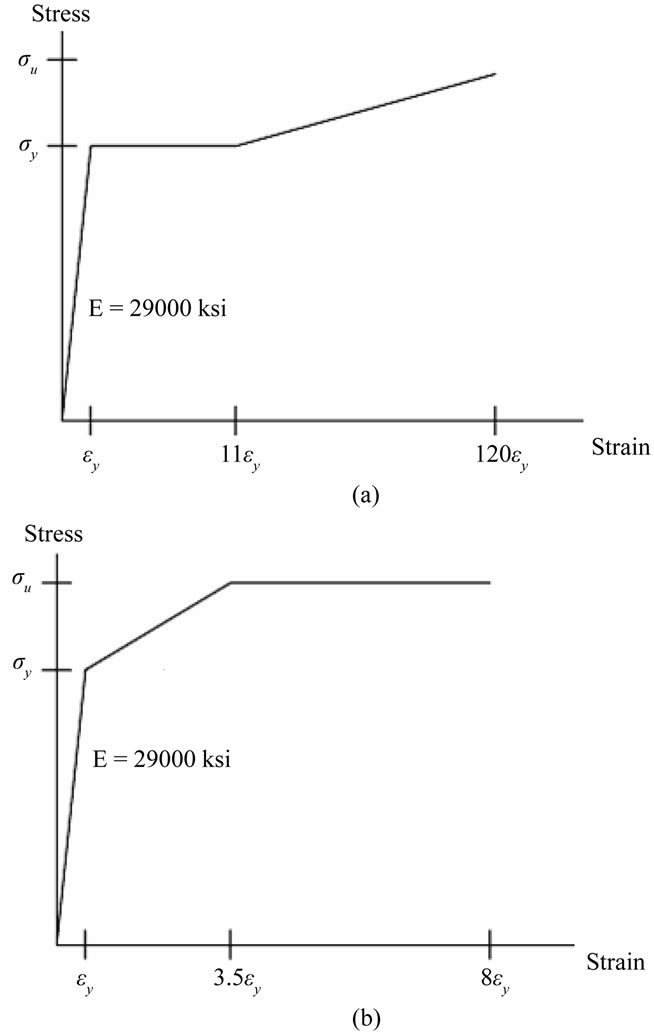
Figure 4. Stress-strain diagrams (a) End-plate material; (b) A325 bolt material, (1 Ksi = 6.89 MPa).
Mises yield criterion. If the effective strain becomes greater than yield strain, then the element has yielded and the elastic modulus can no longer be used. For all such yielded plate elements the elastic modulus is set to zero. After several trials, it was determined that to best calibrate the FE model with the experimental results and avoid getting singular stiffness matrix the definition of secant modulus of elasticity should be used in the FE method. Thus for such elements, the reduced modulus of elasticity can be determined for the end-plate material from; as follows:
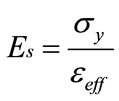 (1)
(1)
in which 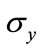 is the yield stress of the end-plate material. Similarly, for the bolt shank material, the reduced modulus of elasticity is also defined. In each load step, the inelastic modulus of the yielded elements is rearranged into their secant values.
is the yield stress of the end-plate material. Similarly, for the bolt shank material, the reduced modulus of elasticity is also defined. In each load step, the inelastic modulus of the yielded elements is rearranged into their secant values.
Before applying any load, the pretension forces are applied at the bolt end node; as presented in Figure 3. Once all bolts are pretensioned, an external load is applied incrementally by considering all the nonlinearities due to material and contact geometries. Displacements of the bolt end nodes are then applied as specified displacements for the external loadings. Then the external loading is applied in small increments. At any load step, the support conditions at the nodes on the back of the end-plate are considered unknown and then they must be determined before computation of deflections and stresses. These support conditions are iteratively determined at every load step by trial and error. To start at the pretension load level, the nodes at the back of the end-plate are assumed to be supported. Excessive yielding in the end-plate or rupture of the bolt are the failure criteria defined to stop the analysis. Equations that describe each failure criterion are as follows;
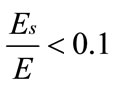 (2)
(2)
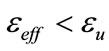 (3)
(3)
in which Es and E are the reduced secant modulus and Young’s modulus of the end-plate material and εeff and εu are the effective strain and ultimate strain of the bolt material.
Once the FE mathematical model created, one needs to verify the results. For verifying the results of the FE analysis and the implemented model, an FE complete model using the ANSYS computer program was also created. For the modeling purposes, first the beam and column are modeled and meshed with three dimensional solid elements (ANSYS SOLID45 element). Bolt heads, nuts and shanks are then modeled using the same elements. In order to model the contact surfaces, contact elements are implemented in the model (ANSYS CONTACT174 element). The contact elements are used in the following interface locations: between end-plate and column flange, between bolt head and end-plate, between nut and column flange, and between the shank and the hole inside the end-plate. The FE model of the connection in the ANSYS program, as well as the components of the connections, is given in Figure 5.
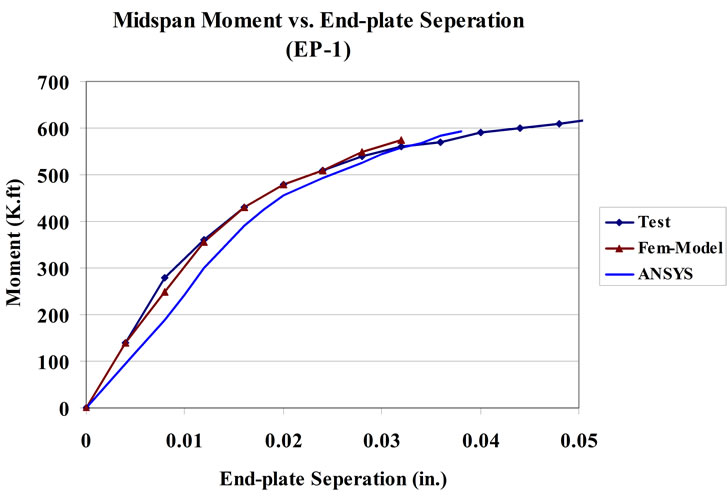
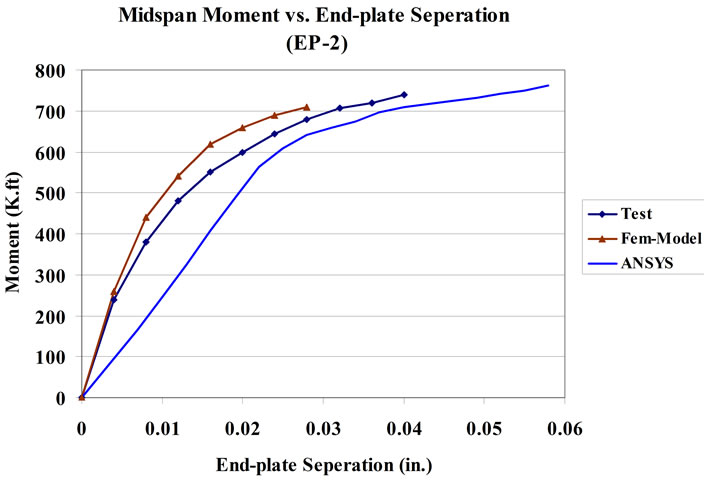
The experimental data obtained by Ghassemieh et al. (1983) as well as the results from the ANSYS program were used to validate the FE model developed. The geometrical dimensional details of the experimental specimens are given in Table 1 and Figure 6. For analysis purposes and for making the appropriate comparisons, the material yield and ultimate stresses obtained from the coupon tests are used in the analysis of the FE model as well as the ANSYS computer model. The comparison of typical three-dimensional FE and experimental results are depicted in Figures 7 and 8, in which end-plate separation measured at the beam tension flange and near bolt forces are displayed. For comparison with the test results,

Figure 5. ANSYS finite element complete model of the endplate connection.
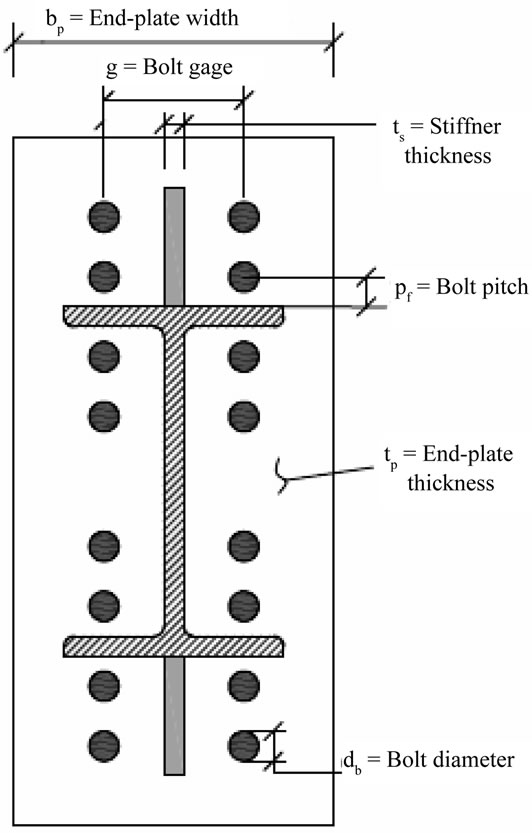
Figure 6. End-plate connection with significant dimensional variables.
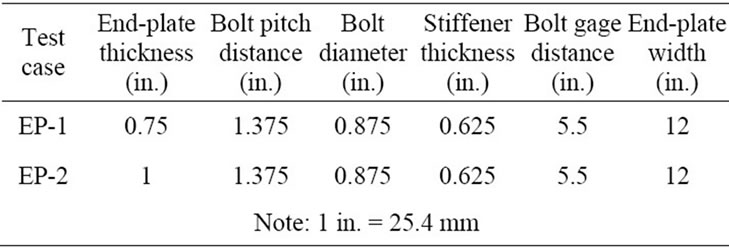
Table 1. End-plate moment connection test specimen geometries (Ghassemieh et al. [1983]).
 (a)
(a)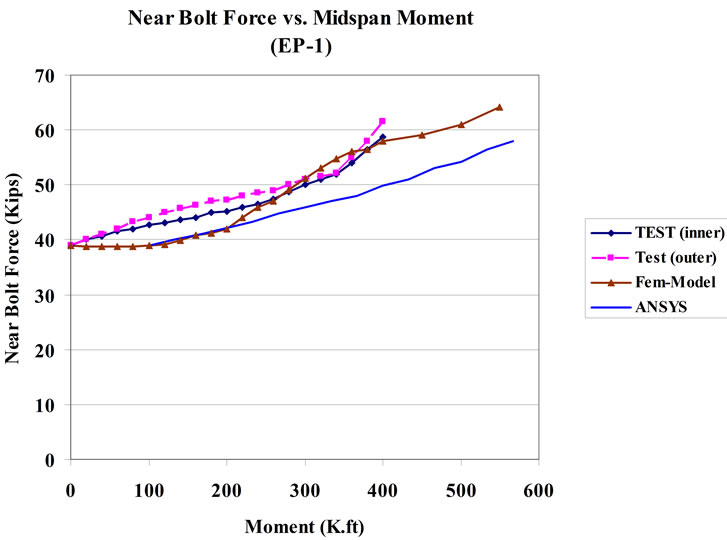 (b)
(b)
Figure 7. FE and test results: (a) End-plate separation; (b) Near-bolt force (1 in. = 25.4 mm and 1 kip-ft = 1.356 kN-m).
the end-plate separations and the bolt forces from the FE model and ANSYS program are plotted with respect to the mid-span moment. In Figures 7(b) and 8(b) “near bolt out” refers to the bolts below the tension flange and “near bolt in” refers the bolts above the tension flange. These plots indicate that the mathematical model with the T hanger analogy used in the FE modeling gives results that measure up closely to ANSYS complete model results and compare well with connection test results. In both cases, excellent agreement was found between predicted and measured plate separation as well as bolt
 (a)
(a)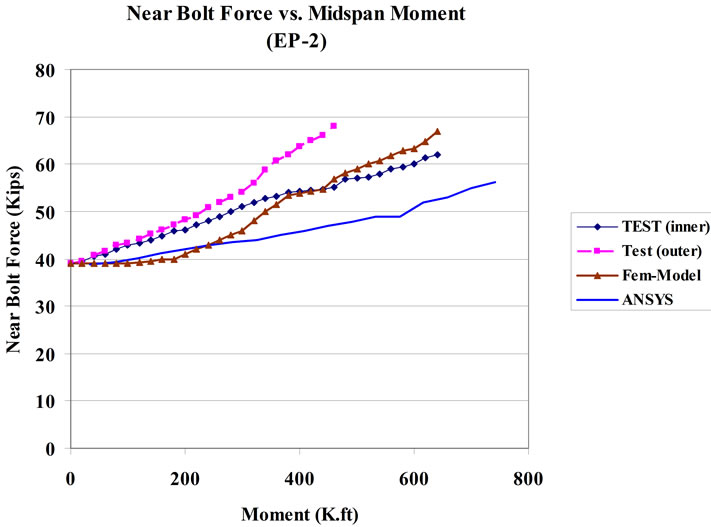 (b)
(b)
Figure 8. FE and test results: (a) End-plate separation; (b) Near-bolt force (1 in. = 25.4 mm and 1 kip-ft = 1.356 kN-m).
forces. Overall correlation between the FE mathematical model as well as ANSYS complete model and experimental results are considered very good due to the differences within 10%.
3. Parametric Study
A parametric study is conducted in order to determine the effect of various geometric and force-related variables on the prediction of the maximum end-plate displacement, the maximum strain on the end-plate, and the axial force in the near bolts. The most significant geometrical variables related to the end-plate connection as shown in Figure 6 are identified as follows: tp = thickness of endplate; Pf = bolt pitch (perpendicular distance from a face of the flange to the center line of a near bolt); db = bolt diameter; ts = stiffener thickness; g = bolts gage (horizontal distance between vertical bolt rows), bp = width of the end-plate; and ws = size of the fillet weld connecting the end-plate to the beam flange. The significant forcerelated independent variable is F = beam flange applied force. The geometrical variables are non-dimensionalized with respect to the end-plate width, bp, resulting in five independent geometric parameters, as follows:
Plate thickness parameter 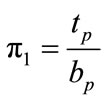 (4)
(4)
Bolt pitch parameter 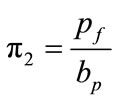 (5)
(5)
Bolt diameter parameter 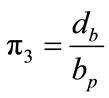 (6)
(6)
Stiffener thickness parameter 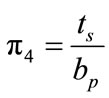 (7)
(7)
Bolt gage parameter 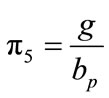 (8)
(8)
Force parameter 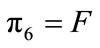 (9)
(9)
The force parameter has units of force. Additional parameters representing two way bending stiffness of the end-plate in the bolt pitch and in the bolt gage directions are also considered in order to place emphasis on the bending behavior as well as improve end results. These parameters are defined as:
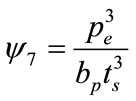 (10)
(10)
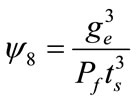 (11)
(11)
in which pe and ge represent the effective bolt pitch distance and effective bolt gage distance and are defined as:
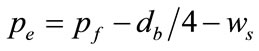 (12)
(12)
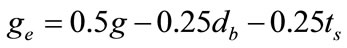 (13)
(13)
Those additional parameters has unit of (length)-1. These dependent parameters are developed to characterrize the behavior of the connections. The parametric study is limited to practical ranges of the various geometric and force parameters. To conduct the parametric study, the geometrical variables must be varied within the practical ranges of extended end-plate connections based on common detailing practices as tabulated in Table 2. The parametric study is organized into three categories based on the plate thickness parameter π1: (1) Minimum values of π1; (2) intermediate values of π1, and (3) maximum values of π1. In each category, the value of π1 is held constant, and the values of π2 to π5 are varied through minimum, intermediate, and maximum levels, one at a time. Based on the combination of the aforementioned variables, by keeping each variable at its intermediate value one at a time while varying other variables from minimum to maximum, 256 cases of different end-plate
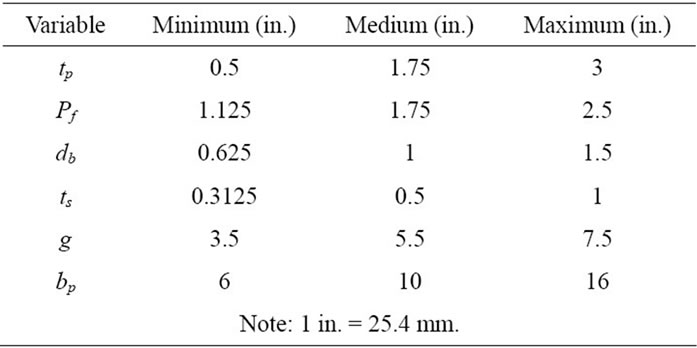
Table 2. Selected range for various geometric variables.
geometry were obtained. Of all the cases generated, removing the unfeasible practical and identical cases and keeping the practical cases, only the twenty five most proportional cases remained for the parametric study. Therefore, the remaining twenty five cases generated were analyzed using the FE analysis to find maximum end-plate separation, maximum strain in the end-plate and near bolt force at various load levels until failure occurred. The aforementioned quantities were used to characterize the behavior of the end-plate connection. The end-plate separation represents the strength, and the maximum strain corresponds to the stiffness of the endplate; whereas the near bolt force signifies the strength of the connecting elements. The data obtained are used to develop the database for the neural network analysis. As described, nearly four hundred sample points have been prepared for the modeling.
4. Aritificial Neural Networks
Artificial Neural Network (ANN) is one of the expert methods of regression which is used in simulation and describing highly nonlinear and complex modeling in many branches of science and engineering. The basic form of a typical artificial neural network is called a multilayer feed-forward neural network; and the most popular form, the three-layer feed-forward neural network, is shown in Figure 9. It consists of three layers of processing elements (neurons or nodes) with connections linking the nodes in successive layers. The first layer consists of n0 input nodes, one for each normalized input variable xi (i = 1, 2, ···, n0). The initial layer consists of n1 hidden nodes, one for each intermediate variable yj (j = 1, 2, ···, n1). Both layers have an additional bias input (indicated with input equals 1.0), which enables the mapping to represent the output level corresponding to zero inputs. At last, the final layer consists of n2 output nodes, one for each output variable zk (k = 1, 2, ···, n2). The input hidden layer transformation performs a continuous nonlinear mapping of the n0 input values xi to the intermediate variables yj; the transformation parameters are weights wij . In a similar way, the hidden output layer transformation performs a mapping (linear or nonlinear) of the n1 intermediate variables yj to the output variables zk; the parameters of this mapping are the weights vij.
ANN training is a procedure which determines the weights associated with the network in the most optimal way using an appropriate algorithm. Haykin (1999) has indicated that many researchers have reported difficulties in training the network parameters caused by parameter interdependence, parameter insensitivity, and several local optima [15]. In the next section, procedures of optimizing topology of ANN, selection of important feature(s) and network training have been described in brief.
5. Optimizing Network Topology and Training Procedure
Two important issues, inputs of model and obtaining the best network topology, affect the performance of each ANN models highly. In the training phase making artificial neural networks operational, the objective is to determine the final wij and vjk in such a way that some measure of fitness, such as sum square error of residual, becomes minimized. This procedure must be done after adjusting the network topology and inputs of models, and its performance highly affected by the mentioned items. In this case, the artificial neural network training exercise becomes an unconstrained, nonlinear optimization problem in the weight space, network topology and model inputs, so an appropriate algorithm may be used to solve this problem. It may be known as the most important topic of system identification to achieve the best performance of simulation between different model features. One of the best methods to optimize these complicated problems is suing heuristic approaches such as Genetic algorithm (GA). GA is considered to be a heuristic, probabilistic, combinatorial, search-based optimization technique based on the biological Darwinian approach in natural evolution developed by Holland (1975) [16] and developed by Goldberg (1989) in its robustness for solving nonlinear, optimization problems [17,18]. Montana and Davis (1989) and Maniezzo (1994) applied SGA in training a back-propagation neural network [19-21]. In the current paper, GA has been used to optimize combination of model inputs, ANN topology (number of nodes in hidden layer) and parameters of learning algorithms. To achieving the best performance of ANN modeling, the next steps have been done successively• In the first step, the whole dataset have been divided to three independent sections. The first subset is adjusted to training phase (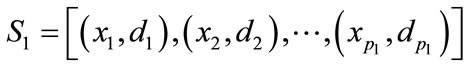 ), the second for cross validation of the training procedure
), the second for cross validation of the training procedure
(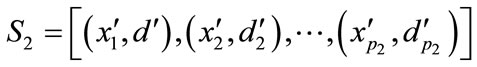 ) and the last one for test of the created final model
) and the last one for test of the created final model
(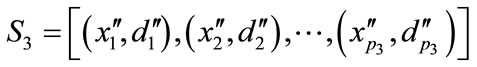 ) [15,16]. The
) [15,16]. The
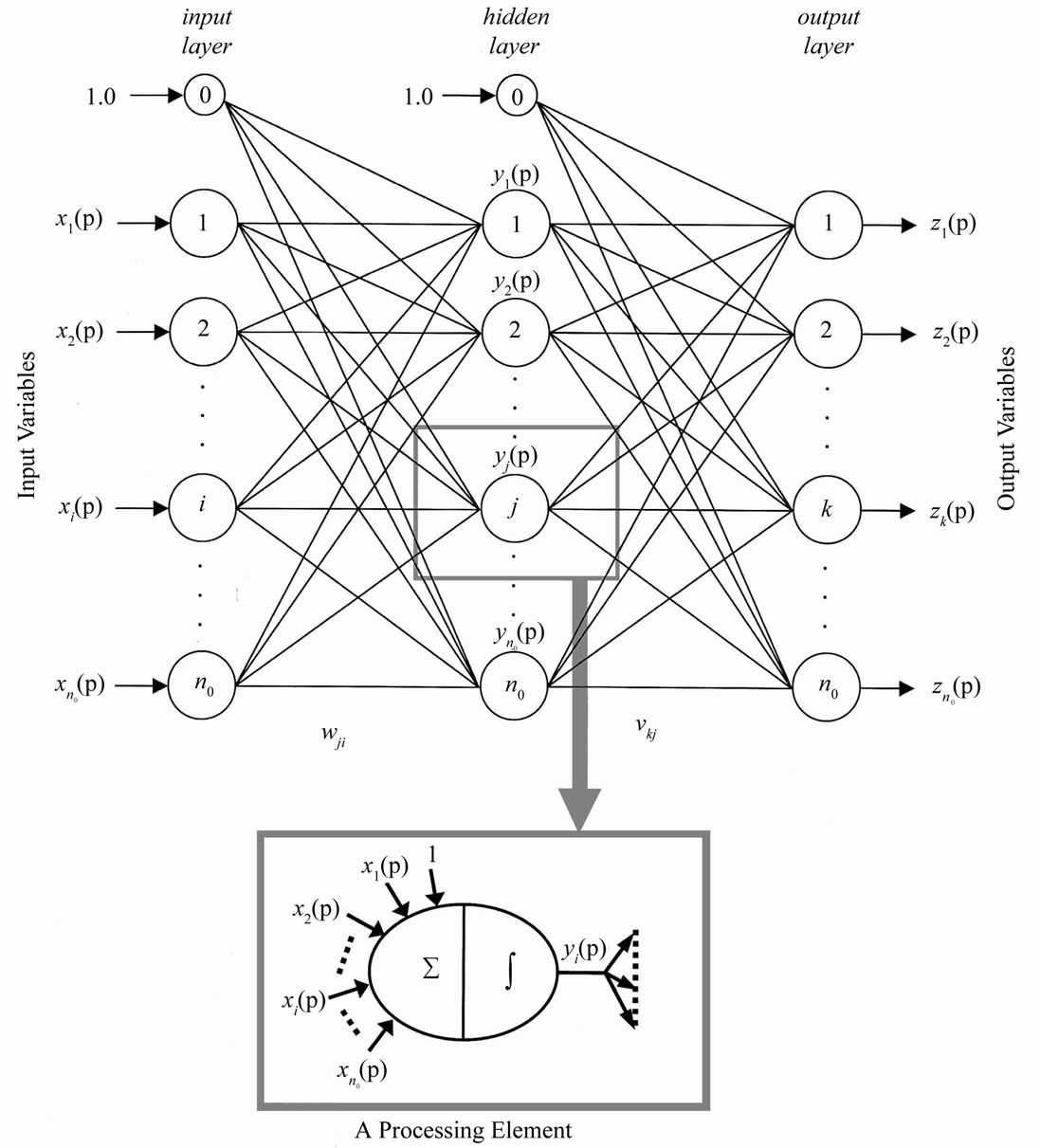
Figure 9. Structure of three-layer feed-forward artificial neural network.
important reason of using the cross validation subset is evaluation of modeling procedure by means of over fitting occurrence [21,22]. Sixty percent of the whole dataset has been specified to be gathered from training, fifteen percent from online validation, and twenty five percent from testing.
• As mentioned before, GA has been used to determine the best ANN topology, learning parameters and inputs. In each population of GA, number of nodes in hidden layer, parameters of learning paradigm and indexes of used inputs have been included. After determining these parameters for each population, ANN has been trained via cross validation evaluation to preserve model from over fitting effect. Validation of model has been done via mean sum square error in each simulation. Training, cross validation and testing subset have been constant during this optimization. Finally, after achieving the best topology and parameters, test set has been run with the best model [21,22].
Selected model inputs have been evaluated using mathematical sensitivity analysis. This clarified effectiveness of the selected inputs versus the trained model and the observed results, in the next section it is described in brief.
6. Sensitivity Analysis
By using sensitivity analysis, the model’s response will be evaluated with respect to change in input parameters, and the uncertainty of the calibrated model resulting from uncertainties associated with the input parameters, such as stresses, forces, boundary, etc, will be quantified. The main advantage of performing the sensitivity analysis is to identify sensitivity parameters or processes associated with model output. In neural network modeling, like any mathematically based model, sensitivity analysis provides feedback as to which input parameters are the most significant. Considering S to be a measure of the impact of change in one parameter on the output resultthe sensitivity, Sij of the yi model dependent variable due to the change in the input parameter, xj can be expressed as:
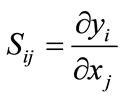 (14)
(14)
where i is the index for model’s ith dependent variable (i.e., model output), j is the index for the jth model input parameter. For a model with n output parameters and m input variables, the number of sensitivity coefficients that could be generated is given by n×m. The unit of Sij, is the unit of yi over xj, and 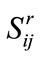 is dimensionless coefficient defined as:
is dimensionless coefficient defined as:
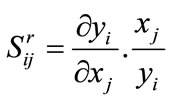 (15)
(15)
It must be emphasized that the computation of sensitivity coefficients in a typical input-output model is not a trivial task, as we are not faced with a closed form function but a complex procedure to convert input to output. As a result, some numerical schemes should be employed to compute those coefficients. For the networks which are developed in this research, sensitivity coefficients are computed using the mean value of each parameter as a base value, having a bound defined as ±σ (coefficient of variance).
7. Modeling Results
Five type models (eighteen models) to evaluate end-plate separation, X-direction stress in end-plate, Y-direction stress in end-plate, near bolt force and far bolt force (Model i) have been organized for comparing soft computing versus nonlinear regression type simulation. All models have been induced with three layers (input layer, hidden layer and output layer), number of nodes in input layer and hidden have been optimized via GA as a model inputs and hidden layer node respectively and output layer has only one node as model target. In Table 3, the
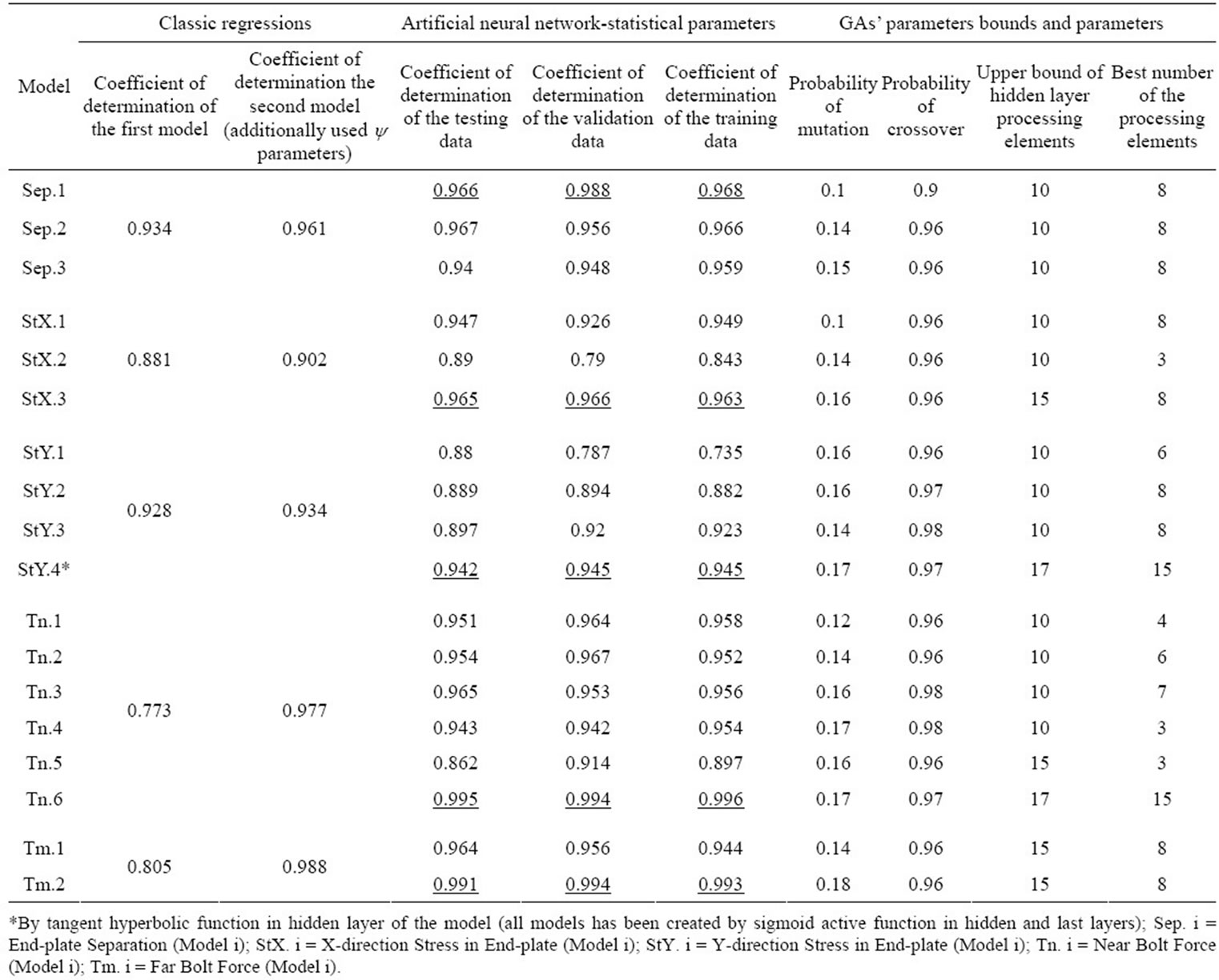
Table 3. Neural networks and genetic algorithm parameters and statistical properties of the models.
optimized parameters of coupled ANNs and GA have been presented. In addition in this table, maximum and optimized numbers of nodes in the hidden layer, probability of mutation and crossover have been presented as well. The findings from the modeling techniques and the optimized ANNs via GA are such that the results of the end-plate separation (maximum displacement) and the near bolt forces are extremely promising and the stresses are very promising. These are the evidence of the power of soft computing in comparison with the classical nonlinear regression analysis. In Table 3, two sets of statistical results in a general regression paradigm were placed to be compared with the artificial neural network results. From the comparison, the high performance of soft computing in regression of complex and nonlinear phenomena was shown. In Table 4, the sensitivity analysis results of the optimized neural network outputs are compared with the independent parameters of the models. At first, after creating some models and comparing sensitivity results, in order to achieve optimally maximum separation, the y7 and y8 parameters were eliminated and only the πi terms are incorporated, while in estimating other dependent parameters, all independent parameters πi and yi are incorporated entirely in the analysis. From the results of this table, it is clear that the yi parameters did not contribute greatly in the modeling as the relevant π2 and π5 parameters were already considered in the models and both affect the results. In the end-plate separation and both stress (X and Y directions) models, endplate thickness, bolt pitch and bolt diameter have the highest contribution and the other parameters could be neglected as sensitivity coefficients show in Table 4. In the bolt force models, the bolt diameter and end-plate thickness have the highest impact and the other parameters could be neglected. The results from the overall models indicate that the bolt diameter is most effective and has biggest role in the behavior of the connections.
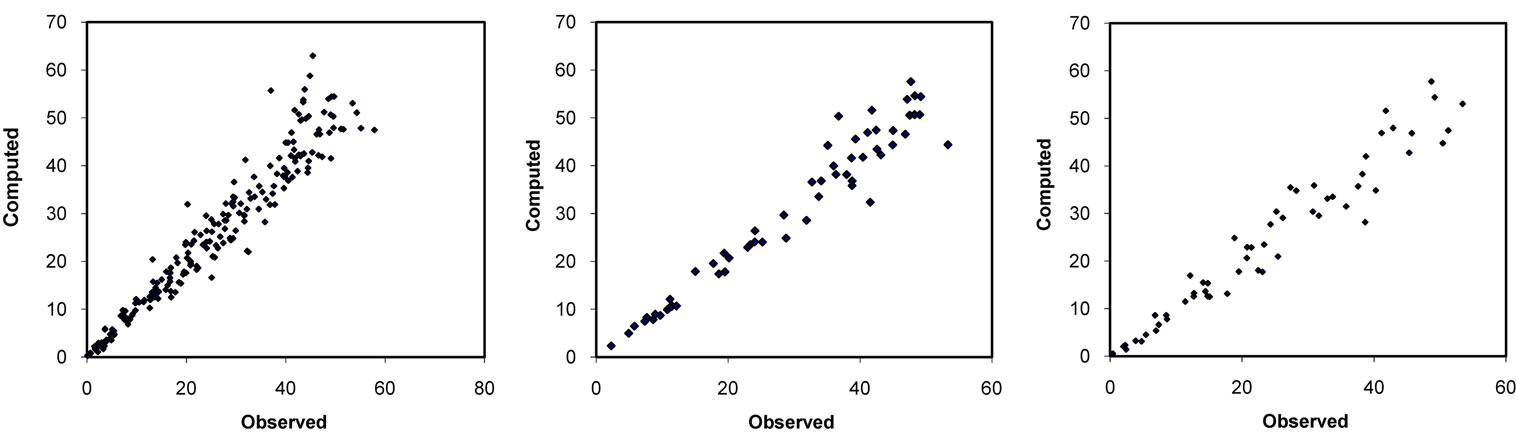
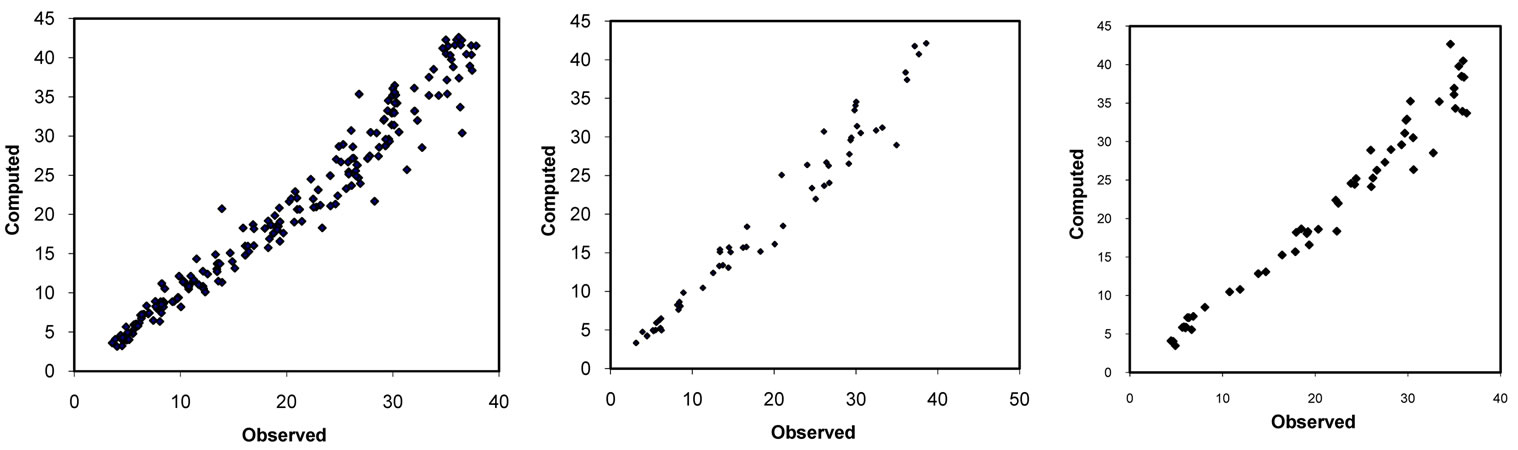
Three types of scatter-plots (calculated versus observed outputs), related to training, validation and testing, are shown in Figures 10 to 14 and are evaluated for the performance of the models. These plots indicate the accuracy of the models and are presented in detail with their statistical properties summary in Table 4.
Overall results show that the neural network procedure can predict results close to the level they were trained for. Also, the results indicate that artificial neural network forecasts were superior to the ones obtained by the linear regression model.
8. Conclusions
This paper has presented a simplified way of modeling and determining the performance and behavior of the stiffened end-plate moment connections. A three dimensional nonlinear finite element model was generated for
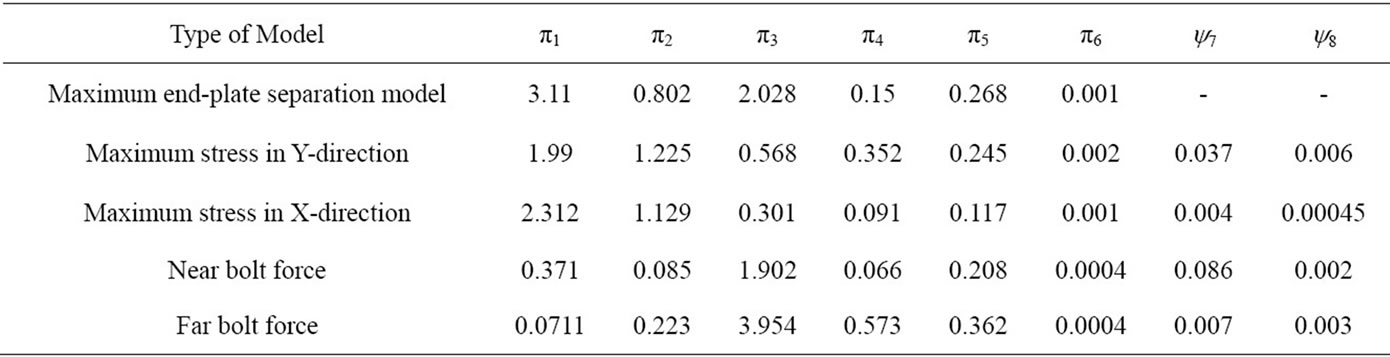
Table 4. Results of the mean sensitivity coefficients (training, validation and testing) of the most valid models.
 (a) (b) (c)
(a) (b) (c)
Figure 10. (a) Training scatter plot of maximum separation; (b) Validation scatter plot of maximum separation; (c) Testing scatter plot of maximum separation.
 (a) (b) (c)
(a) (b) (c)
Figure 11. (a) Training scatter plot of maximum stress in Y direction; (b) Validation scatter plot of maximum stress in Y direction; (c) Testing scatter plot of maximum stress in Y direction.
 (a) (b) (c)
(a) (b) (c)
Figure 12. (a) Training scatter plot of maximum stress in X direction; (b) Validation scatter plot of maximum stress in X direction; (c) Testing scatter plot of maximum stress in X direction.
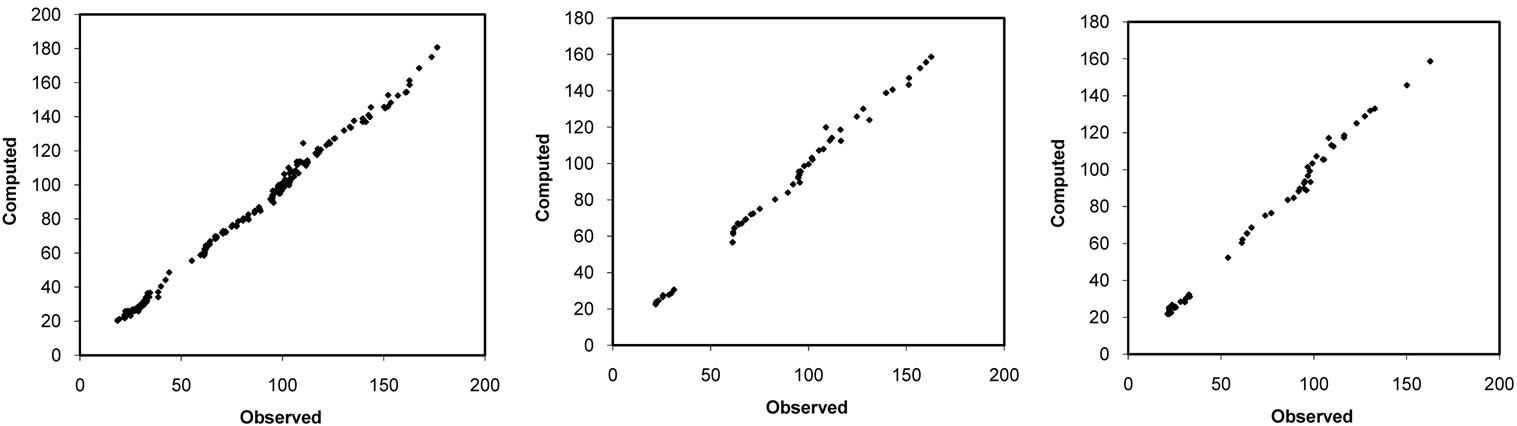 (a) (b) (c)
(a) (b) (c)
Figure 13. (a) Training scatter plot of near bolt force; (b) Validation scatter plot of near bolt force; (c) Testing scatter plot of near bolt force.
extended end-plate moment connections with two rows of bolts above and below the beam flange. Three dimensional isoparametric solid elements were used to model the end-plate, and bolts. The welds were modeled with three dimensional tetrahedral elements as well as rectangular plane stress elements. Nonlinear analyses were adopted to account for material, geometric, and contact phenomena. Bolt pretension criterion was used to simulate the effects of slip critical bolts with proof load. A trilinear material model was used with initial stiffness and post yield stiffness for end-plate and bolt materials. The developed finite element mathematical model and its associated nonlinear algorithm were used to obtain the end-plate separation, end-plate stresses in different direc-
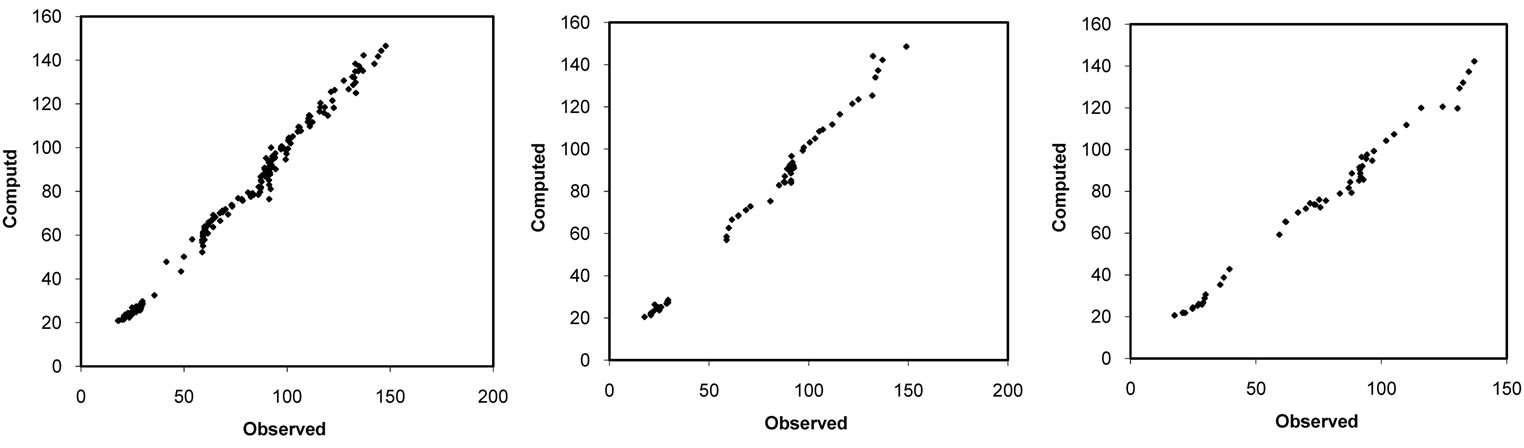 (a) (b) (c)
(a) (b) (c)
Figure 14. (a) Training scatter plot of far bolt force; (b) Validation scatter plot of far bolt force; (c) Testing scatter plot of far bolt force.
tion and near as well as far bolt forces. From the mathematical model investigation, it was concluded that the finite element model behavior was close to the experimental results. Results of the mathematical T hanger model were also verified by ANSYS finite element complete model.
Information from a sufficient number of cases is gathered to conduct a feasibility and sensitivity study so as to select certain parameters from the geometry of the system. All the effective parameters used in the model analysis, such as end-plate width, bolt diameters, welds and all other significant variables, are incorporated in the analysis, and the ranges of the parameters have been restricted to practical ranges. A matrix of twenty five test cases was developed by varying the extended end-plate’s geometric variables within their practical ranges. Finite element analyses were carried out for the selected cases and the results in end-plate separation, end-plate stresses, and bolt forces were obtained.
From the results of the finite element method, optimized neural network procedure was developed and evaluation of the applicability of neural networks for predicting the behavior of the end-plate moment connections are presented and preliminary results are illustrated. The main advantage of the neural network models created were that no particular knowledge was needed about the system being modeled, and unknown effects could be included through a proper design of the input-output patterns. Another benefit was in the relative simplicity of neural network building and the high ability of the networks to reproduce stochastic signals.
The final task was to develop models for predicting the end-plate connection behavior from existing finite element databases, to allow the neural network to contribute a more accurate analysis. The results show that relatively simple neural networks, with an adequate choice of the input data, can achieve reasonably good accuracy. The results suggest that the artificial neural network model could be an important tool for forecasting the behavior of end-plate moment connection, though it cannot replace the actual test experiments, but it can complement it with more required information. It is worthwhile to say that this type of soft computing can be used for modeling connections subjected to cyclic loadings; which has not been shown in the literature yet.
REFERENCES
- N. Krishnamurthy, “Analytical Investigation of Bolted Stiffened Tee Stubs,” Report No. CE-MBMA-1902, Vanderbilt University, Nashville, 1978.
- Adelaide Indoor Sports Centre, “Manual of Steel Construction,” 8th Edition, American Institute of Steel Construction, Chicago, 1980.
- N. Krishnamurthy, “Fresh Look at Bolted End-Plate Behavior and Design,” Engineering Journal, Vol. 15, No. 2, 1978, pp. 39-49.
- M. Ghassemieh, A. R. Kukreti and T. M. Murray, “Inelastic Finite Element Analysis of Stiffened End-Plate Moment Connections,” Research Report No. FSEL/AISC 83-02, University of Oklahoma, Norman, 1983.
- T. M. Murray and A. R. Kukreti, “Design of 8-Bolt Stiffened Moment End-Plates,” Engineering Journal, Vol. 25, No. 2, 1988, pp. 45-52.
- Adelaide Indoor Sports Centre, “Manual of steel construction,” 9th Edition, American Institute of Steel Construction, Chicago, 1989.
- A. R. Kukreti, T. M. Murray and M. Ghassemieh, “Behavior and Design of Large Capacity Moment End-Plates,” Structural Engineering, Vol. 116, No. 3, 1990, pp. 809-828. doi:10.1061/(ASCE)0733-9445(1990)116:3(809)
- M. R. Bahaari and A. N. Sherbourne, “Structural Behavior of End-Plate Bolted Connections to Stiffened Columns,” Structural Engineering, Vol. 122, No. 8, 1996, pp. 926-935. doi:10.1061/(ASCE)0733-9445(1996)122:8(926)
- E. Sumner, “Unified Design of Extended End-Plate Moment Connections Subject to Cyclic Loading,” Ph.D. Dissertation, Virginia Polytechnic and State University, Blacksburg, 2003.
- S. Gang, S. Yongjiu, W. Yuanqing, L. Shafu and C. Hong, “Finite Element Analysis and Tests on Bolted End-Plate Connections in Steel Portal Frames,” Advances in Structural Engineering, Vol. 7, No. 3, 2004, pp. 245-256. doi:10.1260/136943304323213193
- S. Yongjiu, S. Gang and W. Yuanqing, “Experimental and Theoretical Analysis of the Moment—Rotation Behavior of Stiffened Extended End-Plate Connections,” Journal of Constructional Steel research, Vol. 63, No. 9, 2007, pp. 1279-1293. doi:10.1016/j.jcsr.2006.11.008
- R. Srouji, A. R. Kukreti and T. M. Murray, “Strength of Two Tension Bolt Flush End-Plate Connections,” Research Report No. FSEL/MBMA 83-03, University of Oklahoma, Norman, 1983.
- B. Bose, Z. M. Wang and S. Sarkar, “Finite Element Analysis of Unstiffened Flush End-Plate Bolted Joints,” Structural Engineering, Vol. 123, No. 12, 1997, pp. 1614-1621. doi:10.1061/(ASCE)0733-9445(1997)123:12(1614)
- B. M. Broderick and A. W. Thomson, “The Response of Flush End-Plate Joints under Earthquake Loading,” Journal of Constructional Steel Research, Vol. 58, No. 9, 2002, pp. 1161-1175. doi:10.1016/S0143-974X(01)00073-6
- S. Haykin, “Neural Networks: A Comprehensive Foundation,” Prentice-Hall, Upper Saddle River, 1999.
- R. J. Schalkoff, “Artificial Neural Networks,” McGrawHill, Singapore, 1997.
- J. Holland, “Adaptation in Natural and Artificial Systems,” University of Michigan Press, Ann Arbor, 1975.
- D. E. Goldberg, “Genetic Algorithms in Search, Optimization and Machine Learning,” Addison Wesley, Reading, 1989.
- Z. Michalewich, “Genetic Algorithms + Data Structures = Evolution Programs,” Springer-Verlag, Berlin, 1992.
- D. J. Montana and L. Davis, “Training Feed-Forward Neural Networks Using Genetic Algorithms,” Proceedings of the 11th International Joint Conference on Artificial Intelligence, San Mateo, 20-25 August 1989, pp. 762-767.
- V. Maniezzo, “Genetic Evaluation of the Topology and Weight Distribution of Neural Network,” IEEE Transactions on Neural Network, Vol. 5, No. 1, 1994, pp. 39-53. doi:10.1109/72.265959
- M. Nasseri, K. Asghari and M. J. Abedini, “Optimized Scenario of Rainfall Forecasting Using Genetic Algorithms and Artificial Neural Networks,” Expert Systems with Applications, Vol. 35, No. 3, 2008, pp. 1415-1421. doi:10.1016/j.eswa.2007.08.033
NOTES
*Corresponding author.

